数据结构——KD树
KD树(K-Dimensional Tree)是一种用于多维空间的二叉树数据结构,旨在提供高效的数据检索。KD树在空间搜索和最近邻搜索等问题中特别有用,允许在高维空间中有效地搜索数据点。
重要性质
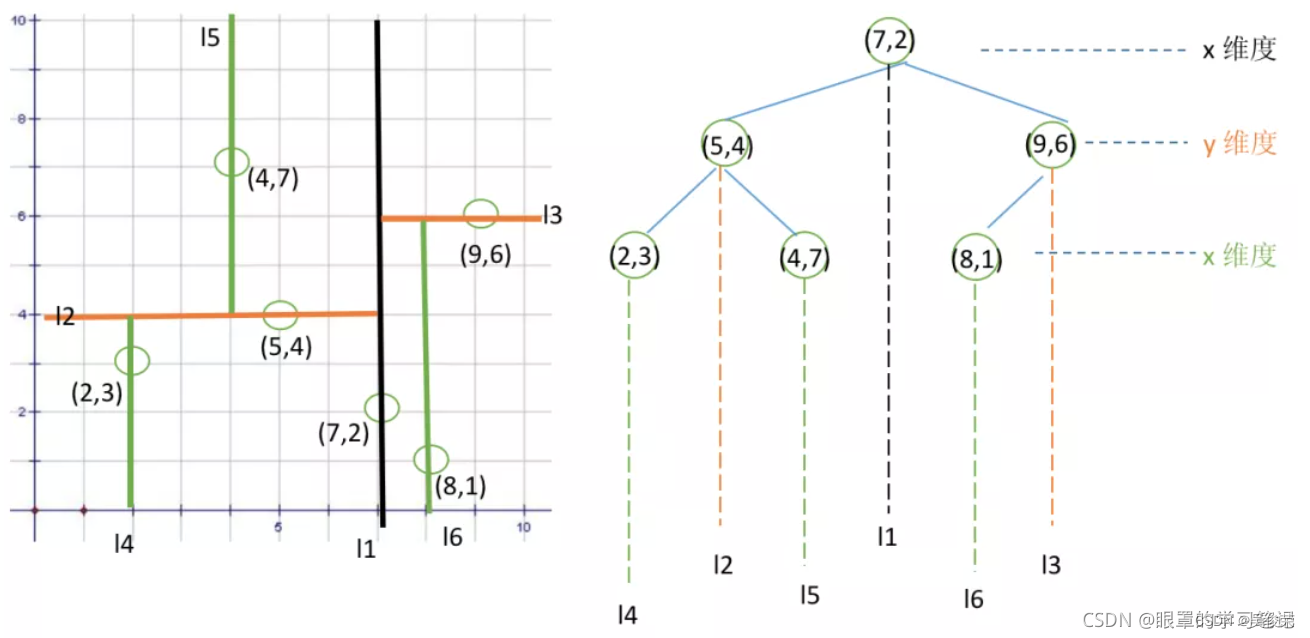
1.分割K维数据空间的数据结构
2.是一颗二叉树
3.切分维度上,左子树值小于右子树值
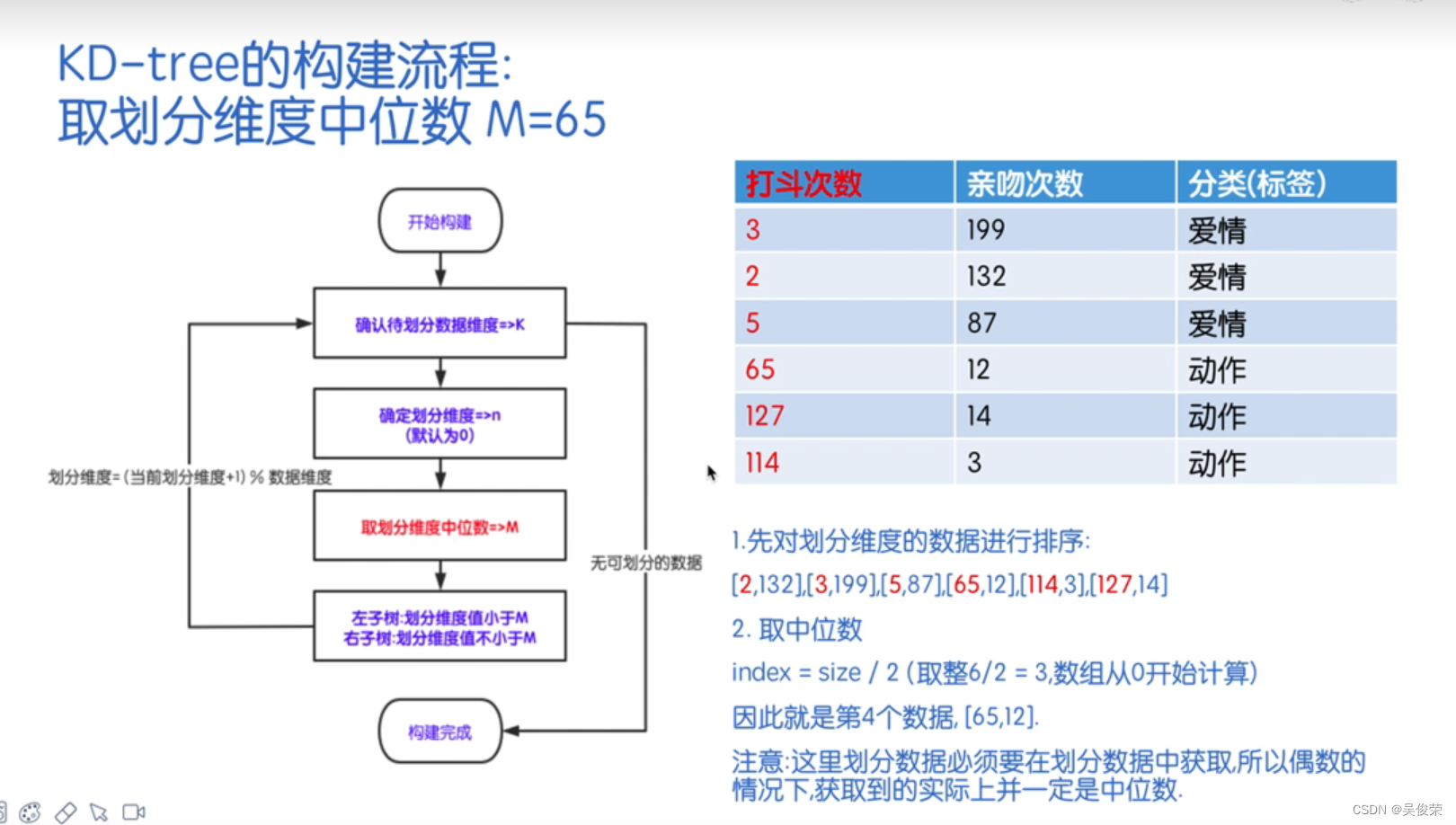
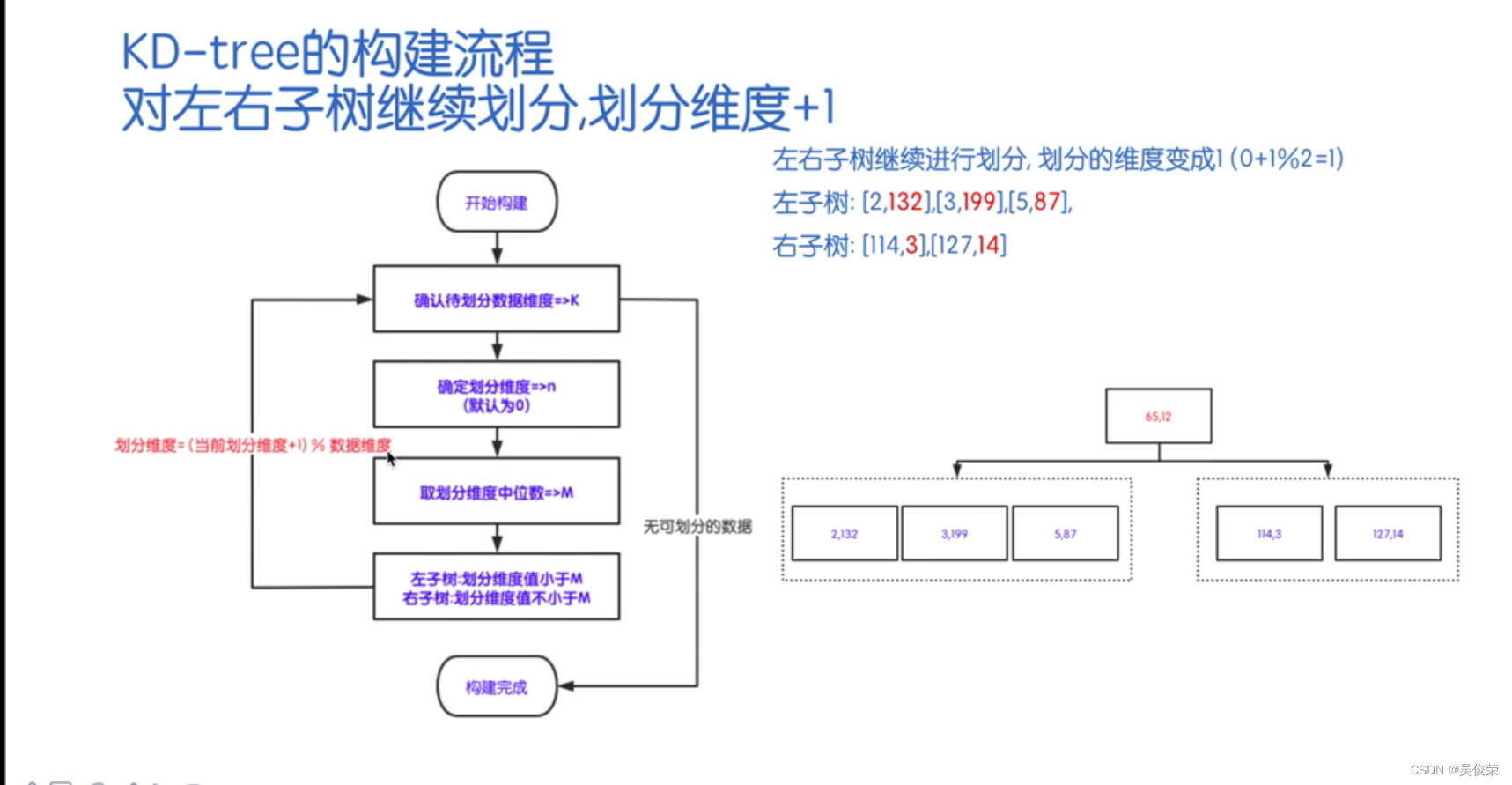
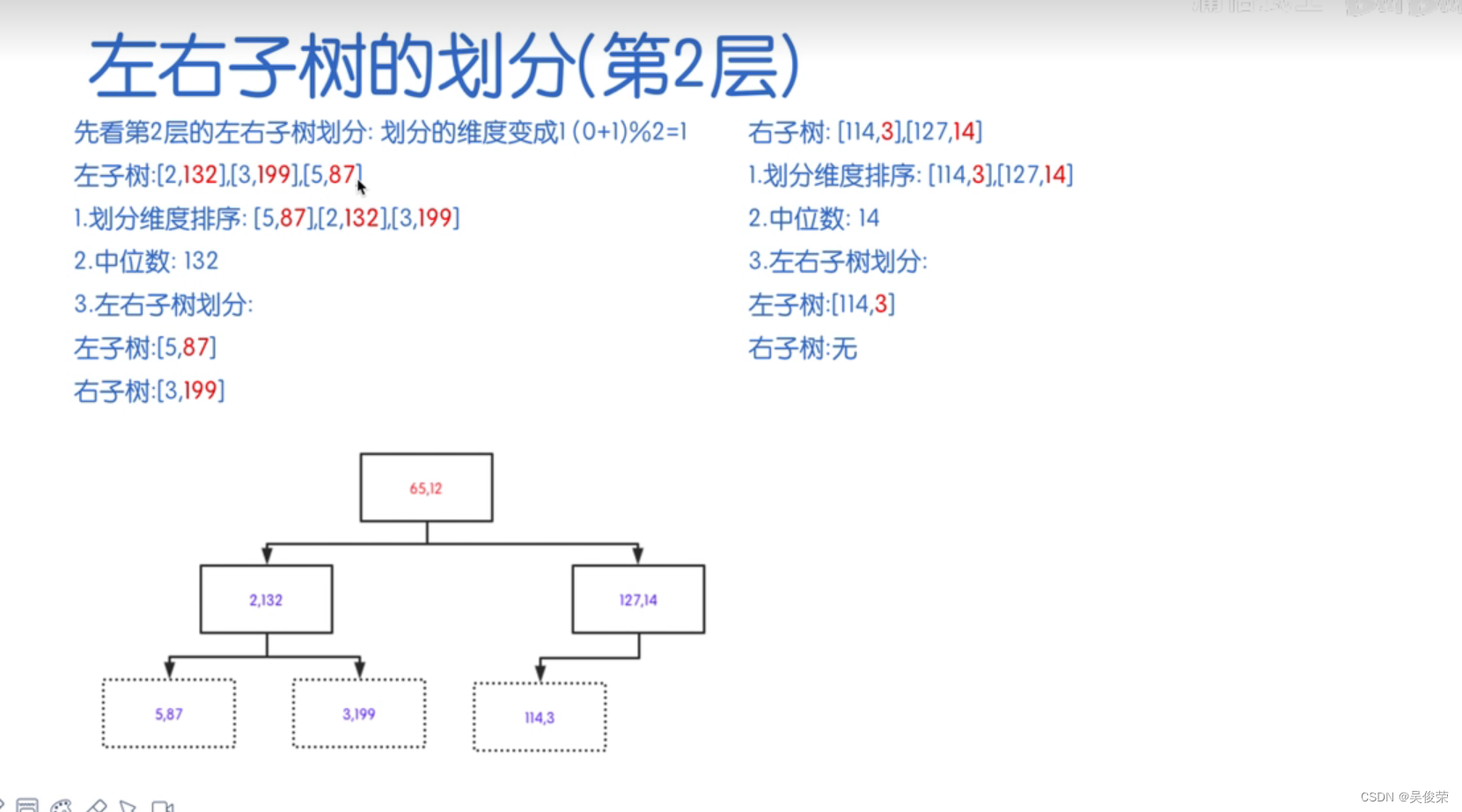
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>// 定义二维点的结构体
struct Point2D {double x;double y;Point2D(double _x, double _y) : x(_x), y(_y) {}
};// 定义KD树节点
struct KDTreeNode {Point2D point;KDTreeNode* left;KDTreeNode* right;KDTreeNode(Point2D _point) : point(_point), left(nullptr), right(nullptr) {}
};class KDTree {
private:KDTreeNode* root;// 构建KD树的递归函数KDTreeNode* buildKDTree(std::vector<Point2D>& points, int depth) {if (points.empty()) {return nullptr;}// 选择轴线,交替选择x和y坐标int axis = depth % 2;// 按轴线排序点if (axis == 0) {std::sort(points.begin(), points.end(), [](const Point2D& a, const Point2D& b) {return a.x < b.x;});} else {std::sort(points.begin(), points.end(), [](const Point2D& a, const Point2D& b) {return a.y < b.y;});}// 选择中间点作为节点int median = points.size() / 2;KDTreeNode* node = new KDTreeNode(points[median]);// 递归构建左子树和右子树std::vector<Point2D> leftPoints(points.begin(), points.begin() + median);std::vector<Point2D> rightPoints(points.begin() + median + 1, points.end());node->left = buildKDTree(leftPoints, depth + 1);node->right = buildKDTree(rightPoints, depth + 1);return node;}// 在KD树中查找最近邻点的递归函数KDTreeNode* findNearestNeighbor(KDTreeNode* node, Point2D target, int depth, KDTreeNode* best, double& bestDistance) {if (node == nullptr) {return best;}// 计算当前节点到目标点的距离double currentDistance = distance(node->point, target);// 更新最近邻点和距离if (currentDistance < bestDistance) {best = node;bestDistance = currentDistance;}// 选择子树int axis = depth % 2;KDTreeNode* nearSubtree;KDTreeNode* farSubtree;if (axis == 0) {if (target.x < node->point.x) {nearSubtree = node->left;farSubtree = node->right;} else {nearSubtree = node->right;farSubtree = node->left;}} else {if (target.y < node->point.y) {nearSubtree = node->left;farSubtree = node->right;} else {nearSubtree = node->right;farSubtree = node->left;}}// 递归搜索更近的子树best = findNearestNeighbor(nearSubtree, target, depth + 1, best, bestDistance);// 如果可能,搜索更远的子树if (shouldSearchFarSubtree(node, target, bestDistance)) {best = findNearestNeighbor(farSubtree, target, depth + 1, best, bestDistance);}return best;}// 计算两点之间的欧几里得距离double distance(Point2D a, Point2D b) {double dx = a.x - b.x;double dy = a.y - b.y;return std::sqrt(dx * dx + dy * dy);}// 检查是否需要搜索更远的子树bool shouldSearchFarSubtree(KDTreeNode* node, Point2D target, double bestDistance) {int axis = node->point.x > target.x ? 0 : 1; // 如果轴线是x,则比较x坐标;如果轴线是y,则比较y坐标double nodeDistance = axis == 0 ? node->point.x - target.x : node->point.y - target.y;return nodeDistance * nodeDistance < bestDistance;}public:KDTree(std::vector<Point2D>& points) {root = buildKDTree(points, 0);}// 查找最近邻点Point2D findNearestNeighbor(Point2D target) {double bestDistance = std::numeric_limits<double>::max();KDTreeNode* bestNode = findNearestNeighbor(root, target, 0, nullptr, bestDistance);return bestNode->point;}
};int main() {// 创建一些二维点std::vector<Point2D> points = {{2.0, 3.0},{5.0, 4.0},{9.0, 6.0},{4.0, 7.0},{8.0, 1.0},{7.0, 2.0}};// 构建KD树KDTree kdTree(points);// 查找最近邻点Point2D target(9.0, 2.0);Point2D nearestNeighbor = kdTree.findNearestNeighbor(target);std::cout << "The nearest neighbor to (" << target.x << ", " << target.y << ") is (" << nearestNeighbor.x << ", " << nearestNeighbor.y << ")" << std::endl;return 0;
}相关文章:

数据结构——KD树
KD树(K-Dimensional Tree)是一种用于多维空间的二叉树数据结构,旨在提供高效的数据检索。KD树在空间搜索和最近邻搜索等问题中特别有用,允许在高维空间中有效地搜索数据点。 重要性质 1.分割K维数据空间的数据结构 2.是一颗二叉树…...
python趣味编程-恐龙克隆游戏
Python 中使用 Turtle 的恐龙克隆游戏免费源代码 使用 Turtle 的恐龙克隆游戏是一个用Python编程语言编码的桌面游戏应用程序。该项目包含在 Chrome 浏览器中克隆实际恐龙游戏的多种功能。该项目可以使正在修读 IT 相关课程的学生受益。这个应用程序非常有趣,可以帮助您学习创…...

【漏洞复现】泛微e-office OfficeServer2.php 存在任意文件读取漏洞复现
文章目录 前言声明一、漏洞描述二、漏洞分析三、漏洞复现四、修复建议前言 泛微e-office OfficeServer2.php 存在任意文件读取漏洞,攻击者可通过构造特定Payload获取敏感数据信息。 声明 请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造…...

基于Yolov8的野外烟雾检测(4):通道优先卷积注意力(CPCA),效果秒杀CBAM和SE等 | 中科院2023最新发表
目录 1.Yolov8介绍 2.野外火灾烟雾数据集介绍 3.CPCA介绍 3.1 CPCA加入到yolov8 4.训练结果分析 5.系列篇 1.Yolov8介绍 Ultralytics YOLOv8是Ultralytics公司开发的YOLO目标检测和图像分割模型的最新版本。YOLOv8是一种尖端的、最先进的(SOTA)模型&a…...

程序员必掌握的核心算法:提升编程技能的关键路径
一:引言 作为程序员,算法是我们编程生涯中的灵魂。算法是解决问题的方法和步骤,它们在计算机科学中扮演着至关重要的角色。无论你是初学者还是经验丰富的专业人士,都需要掌握一些核心算法,因为它们在各种应用场景中频…...

面试算法10:和为k的子数组
题目 输入一个整数数组和一个整数k,请问数组中有多少个数字之和等于k的连续子数组?例如,输入数组[1,1,1],k的值为2,有2个连续子数组之和等于2。 分析 在从头到尾逐个扫描数组中的数字时求出前…...

王道考研操作系统
王道考研操作系统 计算机系统概述操作系统的概念操作系统的特征操作系统的发展历程操作系统内核中断和异常系统调用操作系统结构虚拟机错题 进程与线程进程控制进程通信线程和多线程模…...

HEXO 基本使用
1 新建、编辑并预览文章 1. 新建文章 hexo new [layout] title # 或 hexo n [layout] title创建文章前要先选定模板,在hexo中也叫做布局。hexo支持三种布局(layout):post(默认)、draft、page。我们先介绍如何使用已有布局…...

Webpack Sourcemap文件泄露漏洞
Webpack Sourcemap文件泄露漏洞 前言一、Webpack和Sourcemap1.1 什么是Webpack1.2 什么是Sourcemap二、漏洞利用2.1 使用reverse-sourcemap工具2.1 直接看前端代码三、漏洞挖掘漏洞修复前言 Webpack主要是用于前端框架进行打包的工具,打包后形成.js.map文件,如果.js.map文件…...

WebGL层次模型——单节点模型
目录 多个简单模型组成的复杂模型 层次结构模型 单关节模型 JointModel程序中模型的层次结构 示例程序(JointMode.js) 代码详解 绘制层次模型(draw()) 程序效果 多个简单模型组成的复杂模型 绘制…...

【链表】反转链表 II-力扣 92 题
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…...

【考研数学】高等数学第六模块 —— 空间解析几何(1,向量基本概念与运算)
文章目录 引言一、空间解析几何的理论1.1 基本概念1.2 向量的运算 写在最后 引言 我自认空间想象能力较差,所以当初学这个很吃力。希望现在再接触,能好点。 一、空间解析几何的理论 1.1 基本概念 1.向量 —— 既有大小,又有方向的量称为向…...

巨人互动|Facebook海外户Facebook客户反馈分数
Facebook客户反馈分数是一项用于衡量用户对Facebook产品和服务满意度的指标。该指标被广泛应用于各种调研和评估活动,帮助Facebook了解用户对其平台和功能的意见和建议,并从中识别出改进的机会。 巨人互动|Facebook海外户&Facebook新闻提要的算法&am…...
Tomcat多实例部署和动静分离
一、多实例部署: 多实例:多实例就是在一台服务器上同时开启多个不同的服务端口,同时运行多个服务进程,这些服务进程通过不同的socket监听不同的服务端口来提供服务。 1.前期准备: 1.关闭防火墙:systemctl …...

关于 C/C++ 中在指针前加 const 关键字的作用说明
1. 作用说明: 在指针前加 const 的用途为:不可改变指针指向的内存的值,即将该指向指向的内存中的变量置为只读(read-only) 变量。 但是,可以给 const 的指针赋值,即将具有 const 属性的指针指向别的内存地…...
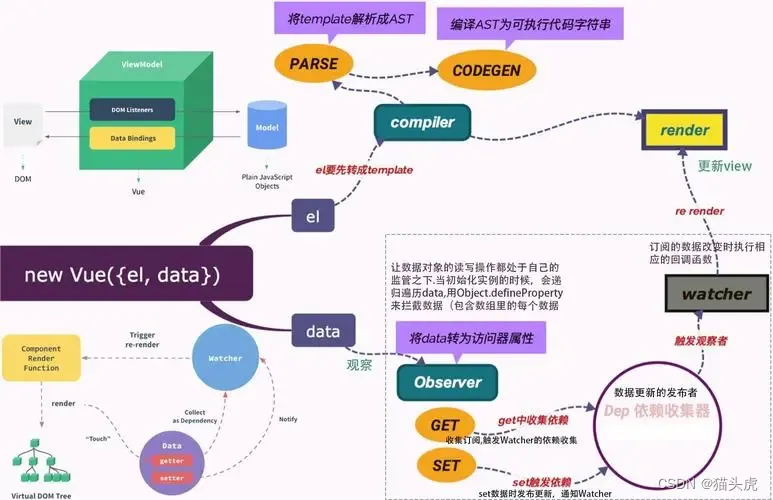
Vue.js新手指南:从零开始建立你的第一个应用
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

【案例】--EasyExcel导入导出文件案例
目录 一、前言二、EasyExcel解析(导入)文件2.1、EasyExcel选型2.2、如何存储excel解析的文件2.3、解析格式规则的excel文件2.4、解析未知格式规则的excel文件三、EasyExcel解析(导出)文件3.1、导出基本代码实现一、前言 最近项目中,需要对excel、csv等文件进行解析,并做相关…...

深入探索图像处理:从基础到高级应用
💂 个人网站:【工具大全】【游戏大全】【神级源码资源网】🤟 前端学习课程:👉【28个案例趣学前端】【400个JS面试题】💅 寻找学习交流、摸鱼划水的小伙伴,请点击【摸鱼学习交流群】 图像处理是计算机视觉领…...
Jetpack Compose基础组件 - Image
Image的源码参数预览 Composable fun Image(painter: Painter,contentDescription: String?,modifier: Modifier Modifier,alignment: Alignment Alignment.Center,contentScale: ContentScale ContentScale.Fit,alpha: Float DefaultAlpha,colorFilter: ColorFilter? …...

UINavigationController内的页面跳转实现 UIViewController 的 present和dismiss动画
UINavigationController内部页面跳转默认为左右切换,但是当我们想向上弹出进入界面,或者向下离开界面时,需要实现UINavigationControllerDelegate 协议自行控制页面的动画(否则直接在navVc上叠加动画会导致动画结束后的那个页面,自…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
