【考研数学】高等数学第六模块 —— 空间解析几何(1,向量基本概念与运算)
文章目录
- 引言
- 一、空间解析几何的理论
- 1.1 基本概念
- 1.2 向量的运算
- 写在最后
引言
我自认空间想象能力较差,所以当初学这个很吃力。希望现在再接触,能好点。
一、空间解析几何的理论
1.1 基本概念
1.向量 —— 既有大小,又有方向的量称为向量,常用从起点指向终点的带箭头的有向线段 A B → \overrightarrow{AB} AB 表示,或用带箭头的小写字母 a → \overrightarrow{a} a 。
向量的大小或长度称为向量的模,向量 a → \overrightarrow{a} a 的模记作 ∣ a → ∣ |\overrightarrow{a}| ∣a∣ 。特别地,模为 1 的向量称为单位向量,模为 0 的向量称为零向量,记作 a → 0 \overrightarrow{a}^0 a0 。大小相等且方向相同的向量相等。
2.向量的坐标 —— 设 i → , j → , k → \overrightarrow{i},\overrightarrow{j},\overrightarrow{k} i,j,k 分别表示 x , y , z x,y,z x,y,z 轴正向的单位向量,设向量 a → \overrightarrow{a} a 在三个坐标轴上的投影分别为 a , b , c a,b,c a,b,c ,由向量的分解得 a → = a i → + b j → + c k → = { a , b , c } \overrightarrow{a}=a\overrightarrow{i}+b\overrightarrow{j}+c\overrightarrow{k}=\{a,b,c\} a=ai+bj+ck={a,b,c} ,称 { a , b , c } \{a,b,c\} {a,b,c} 为向量 a → \overrightarrow{a} a 的坐标。
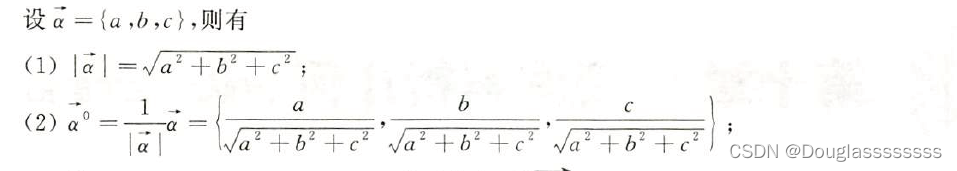
3.向量的方向角和方向余弦 —— 设 a → = { a , b , c } \overrightarrow{a}=\{a,b,c\} a={a,b,c} 为非零向量,则 a → \overrightarrow{a} a 与 x , y , z x,y,z x,y,z 轴正向的夹角,称为此向量的方向角,分别记为 α , β , γ \alpha,\beta,\gamma α,β,γ ,称 cos α , cos β , cos γ \cos\alpha,\cos\beta,\cos\gamma cosα,cosβ,cosγ 为 a → \overrightarrow{a} a 的方向余弦。则 cos α = a a 2 + b 2 + c 2 , cos β = b a 2 + b 2 + c 2 , cos α = c a 2 + b 2 + c 2 \cos\alpha=\frac{a}{\sqrt{a^2+b^2+c^2}},\cos\beta=\frac{b}{\sqrt{a^2+b^2+c^2}},\cos\alpha=\frac{c}{\sqrt{a^2+b^2+c^2}} cosα=a2+b2+c2a,cosβ=a2+b2+c2b,cosα=a2+b2+c2c 显然,有 a → 0 = { cos α , cos β , cos γ } \overrightarrow{a}^0=\{\cos\alpha,\cos\beta,\cos\gamma\} a0={cosα,cosβ,cosγ} , cos α 2 + cos β 2 + cos γ 2 = 1 \cos\alpha^2+\cos\beta^2+\cos\gamma^2=1 cosα2+cosβ2+cosγ2=1 。
4.向量在一个轴(向量)上的投影 —— 设 u u u 为一个数轴, a → \overrightarrow{a} a 为一个向量,过向量的起点 A 和终点 B 作 u u u 轴的垂直面交 u u u 轴于点 A 1 , B 1 A_1,B_1 A1,B1 ,其在 u u u 轴上的坐标分别为 x 1 , x 2 x_1,x_2 x1,x2 ,称 x 2 − x 1 x_2-x_1 x2−x1 为向量 a → \overrightarrow{a} a 在 u u u 轴上的投影,记为 P r j u a → = x 2 − x 1 Prj_u\overrightarrow{a}=x_2-x_1 Prjua=x2−x1 ,且 P r j u a → = ∣ a → ∣ cos ( u , a → ) Prj_u\overrightarrow{a}=|\overrightarrow{a}|\cos(u,\overrightarrow{a}) Prjua=∣a∣cos(u,a) 。
1.2 向量的运算
(一)几何描述
加减法,遵循三角形法则。



(二)代数描述
主要说一下叉乘(向量积)的代数形式:

下面是一些运算的性质:

写在最后
有关向量的基本概念和性质基本就这些,下一篇我们就来看看向量有哪些应用。
相关文章:

【考研数学】高等数学第六模块 —— 空间解析几何(1,向量基本概念与运算)
文章目录 引言一、空间解析几何的理论1.1 基本概念1.2 向量的运算 写在最后 引言 我自认空间想象能力较差,所以当初学这个很吃力。希望现在再接触,能好点。 一、空间解析几何的理论 1.1 基本概念 1.向量 —— 既有大小,又有方向的量称为向…...

巨人互动|Facebook海外户Facebook客户反馈分数
Facebook客户反馈分数是一项用于衡量用户对Facebook产品和服务满意度的指标。该指标被广泛应用于各种调研和评估活动,帮助Facebook了解用户对其平台和功能的意见和建议,并从中识别出改进的机会。 巨人互动|Facebook海外户&Facebook新闻提要的算法&am…...
Tomcat多实例部署和动静分离
一、多实例部署: 多实例:多实例就是在一台服务器上同时开启多个不同的服务端口,同时运行多个服务进程,这些服务进程通过不同的socket监听不同的服务端口来提供服务。 1.前期准备: 1.关闭防火墙:systemctl …...

关于 C/C++ 中在指针前加 const 关键字的作用说明
1. 作用说明: 在指针前加 const 的用途为:不可改变指针指向的内存的值,即将该指向指向的内存中的变量置为只读(read-only) 变量。 但是,可以给 const 的指针赋值,即将具有 const 属性的指针指向别的内存地…...
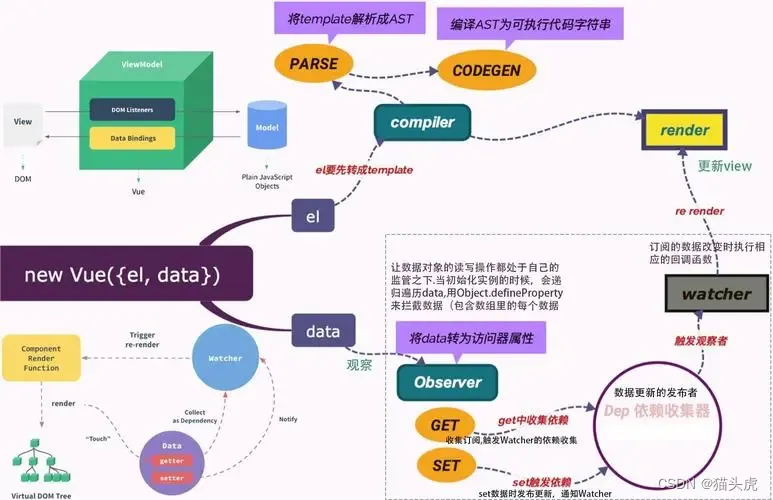
Vue.js新手指南:从零开始建立你的第一个应用
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

【案例】--EasyExcel导入导出文件案例
目录 一、前言二、EasyExcel解析(导入)文件2.1、EasyExcel选型2.2、如何存储excel解析的文件2.3、解析格式规则的excel文件2.4、解析未知格式规则的excel文件三、EasyExcel解析(导出)文件3.1、导出基本代码实现一、前言 最近项目中,需要对excel、csv等文件进行解析,并做相关…...

深入探索图像处理:从基础到高级应用
💂 个人网站:【工具大全】【游戏大全】【神级源码资源网】🤟 前端学习课程:👉【28个案例趣学前端】【400个JS面试题】💅 寻找学习交流、摸鱼划水的小伙伴,请点击【摸鱼学习交流群】 图像处理是计算机视觉领…...
Jetpack Compose基础组件 - Image
Image的源码参数预览 Composable fun Image(painter: Painter,contentDescription: String?,modifier: Modifier Modifier,alignment: Alignment Alignment.Center,contentScale: ContentScale ContentScale.Fit,alpha: Float DefaultAlpha,colorFilter: ColorFilter? …...

UINavigationController内的页面跳转实现 UIViewController 的 present和dismiss动画
UINavigationController内部页面跳转默认为左右切换,但是当我们想向上弹出进入界面,或者向下离开界面时,需要实现UINavigationControllerDelegate 协议自行控制页面的动画(否则直接在navVc上叠加动画会导致动画结束后的那个页面,自…...
PMP对项目管理工作有什么用?
首先,项目管理岗位基本是不限行业的,所以,只要是项目管理相关的岗位,pmp证书都是能起到效果的,不用担心局限性太大,而且,pmp证书是国际证书,无论国企还是外企,都是认可这…...

Python 将‘20230919182550‘ 转换为 ‘%Y年%m月%d日 %H:%M‘
为了将给定的时间字符串 cur_time 转换为指定的格式,可以使用 Python 的 datetime 模块。以下是完成此操作的步骤: 使用 strptime 方法将 cur_time 转换为一个 datetime 对象。使用 strftime 方法将这个 datetime 对象转换为所需的格式。 这是具体的代…...

vue2.0检测无用的代码并删除
(1)、使用 useless-files-webpack-plugin 来查找无用文件 npm i useless-files-webpack-plugin -S (2)、vue.config.js中配置 const UselessFile require(useless-files-webpack-plugin)chainWebpack: config > {config.plu…...
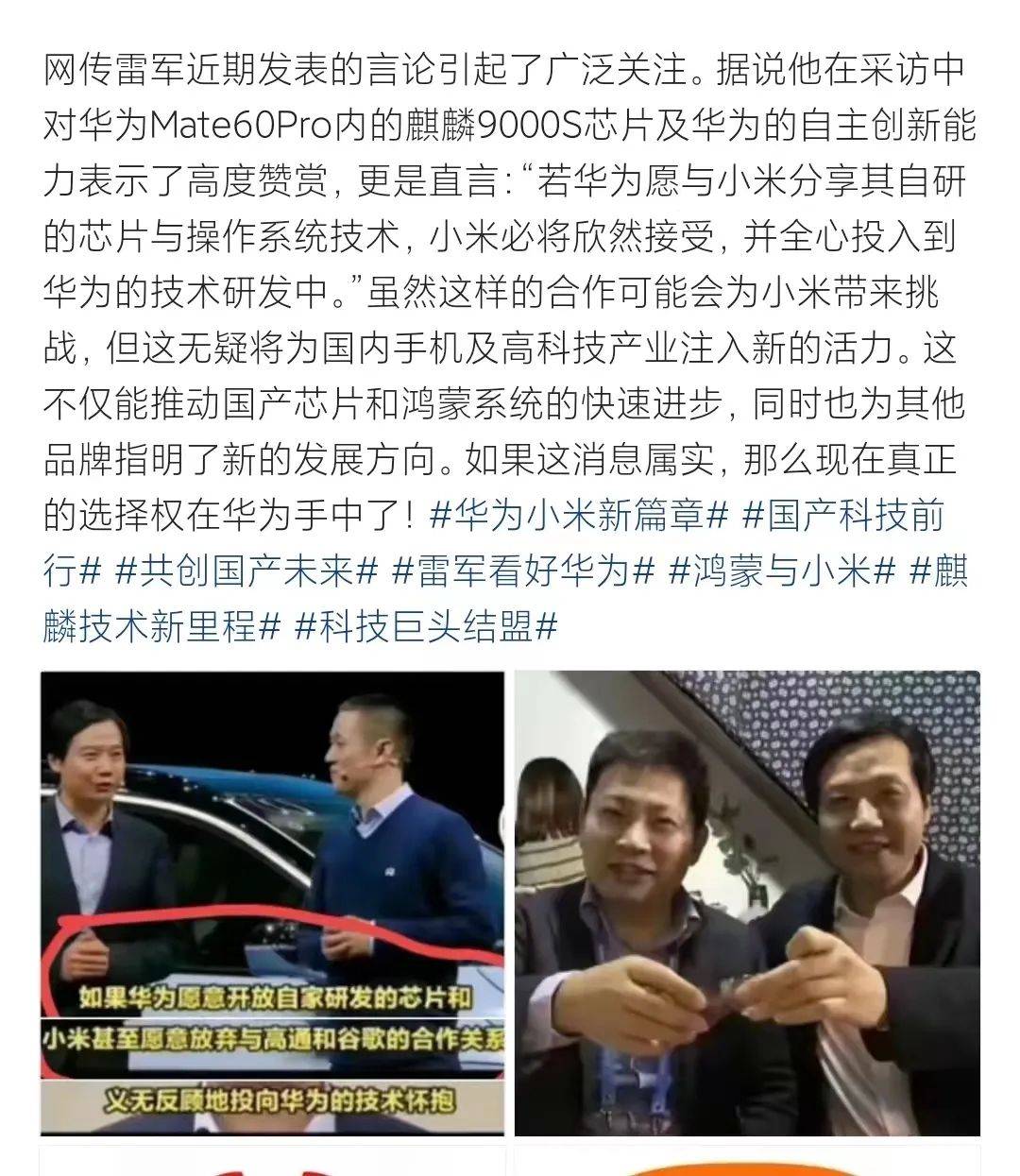
小米华为,化干戈为玉帛!
近日来,手机圈又掀起了各大厂家推出新品的高潮。首先是华为Mate60的推出,其自研的麒麟9000S芯片瞬间点燃了国内手机市场,得到了国内甚至国外业界人士的认可和好评。 而近日网上盛传的小米创始人雷军的“愿意加入华为技术生态圈”的邀请&…...

【文末赠书】SRE求职必会 —— 可观测性平台可观测性工程(Observability Engineering)
文章目录 〇、导读一、实现可观测性平台的技术要点是什么?二、兼容全域信号量三、所谓全域信号量有哪些?四、统一采集和上传工具五、统一的存储后台六、自由探索和综合使用数据七、总结★推荐阅读《可观测性工程》直播预告直播主题直播时间预约直播 视频…...

content生成自定义图标的方式是什么?
animate.css是一个跨浏览器的CSS3动画库,它内置了很多经典的CSS3动画。使用起来很方便。下面我们通过例子讲解如何使用自定义类名和animate.css库实现动画效果。 (1)从animate.css官方网站获取animate.css文件,保存到chapter04目录中。 (2)创建C:\vue\…...

无涯教程-JavaScript - SECH函数
描述 SECH函数返回某个Angular的双曲正割。双曲正割是双曲余弦的倒数。因此,双曲正割的值由等式给出- $$\sinh\left(x\right)\frac {1} {\cosh\left(x\right)} \frac {2} {e ^ x e ^ {-x}} $$ 语法 SECH (number)争论 Argument描述Required/OptionalNumberNumber is the …...
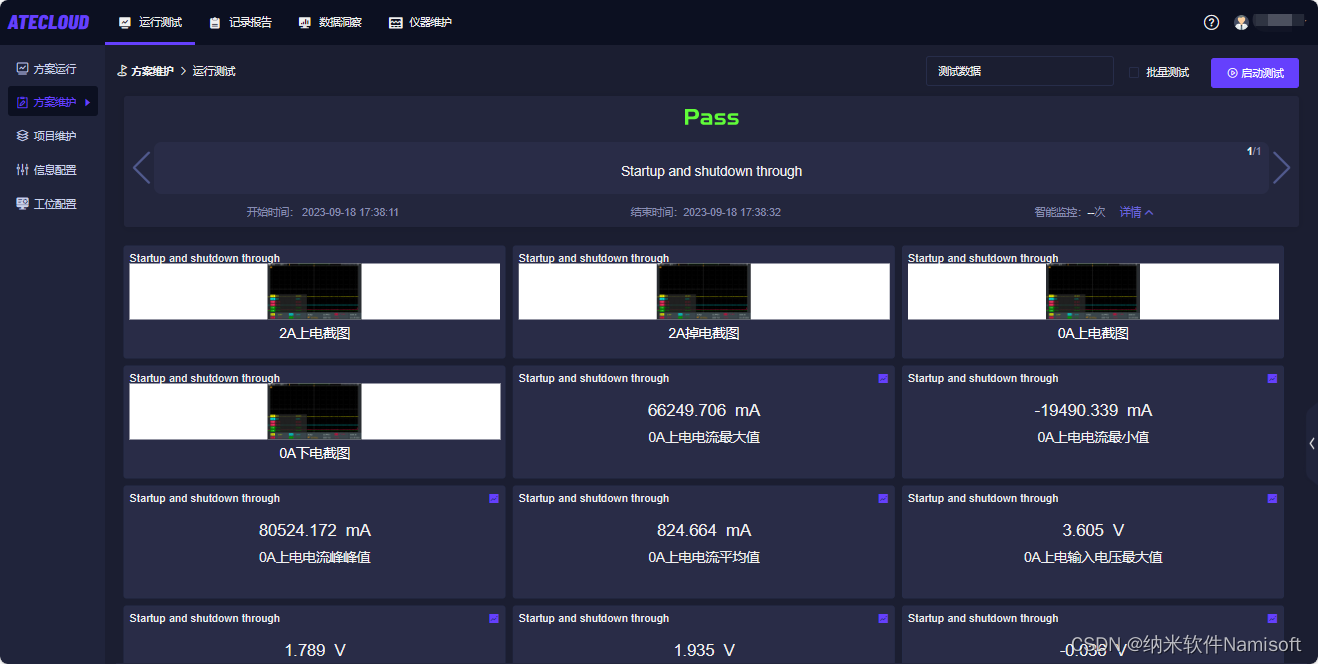
天宇微纳芯片ic测试软件如何测试芯片上下电功能?
芯片的上电与下电功能测试是集成电路生产和研发过程中的关键环节,可以帮助企业确保产品的可靠性、整合性和兼容性,同时提高生产效率和产品质量。 因此在芯片的研发设计中,企业会对芯片的上下电有严格的要求,包括上下电的时序&…...

1万多爱背句子英语口语ACCESS\EXCEL数据库
今天这个数据库包含3个表,一个是分类表,一个是分类章节有,一个是具体句子表,表与表之间可以根据相关ID进行关联,是一个学习英语的好数据,具体请查收截图或样本: 数据有ACCESS数据库文件…...

C++:new 和 delete
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》 文章目录 前言一、C内存管理1.内置类型2.自定义类型3.delete 与 new不匹配使用问题(VS平台下) 二、operator new 与 operator delete函数三、 new 和delete的实现原理内置类型自定义类型 四…...

mysql5.7版本的数据导入到mysql8.0版本需要怎么做
将 MySQL 5.7 版本的数据导入到 MySQL 8.0 版本,由于版本之间可能存在一些差异,需要采取一些步骤来确保数据导入的顺利进行。以下是一般的导入步骤: 备份数据: 在进行任何操作之前,务必备份 MySQL 5.7 数据库。可以使用…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
