【数据结构】长篇详解堆,堆的向上/向下调整算法,堆排序及TopK问题
文章目录
- 堆的概念
- 性质
- 图解
- 向上调整算法
- 算法分析
- 代码整体实现
- 向下调整算法
- 算法分析
- 整体代码实现
- 堆的接口实现
- 初始化堆
- 销毁堆
- 插入元素
- 删除元素
- 打印元素
- 判断是否为空
- 取首元素
- 实现堆
- 堆排序
- 创建堆
- 调整堆
- 整合步骤
- TopK问题
堆的概念
堆就是将一组数据所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足树中每一个父亲节点都要大于其子节点称为大堆(树中每一个父亲节点都要大于其子节点称为小堆)。
性质
①对于大堆(大根堆)来说,堆的顶部也就是数组首元素一定是最大的元素
②对于小堆(小根堆)来说,堆的顶部也就是数组首元素一定是最小的元素
(这两点对于下面的堆排序来说十分重要)
此外,
堆总是一棵完全二叉树,因为堆本身就是二叉树的一种顺序存储结构的实现模式
注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段
图解
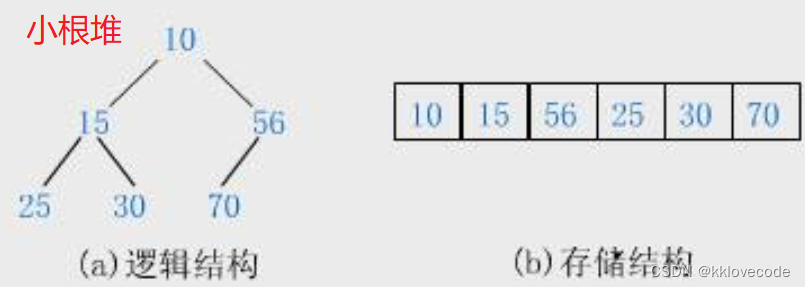
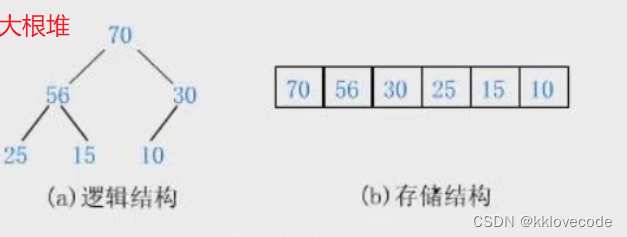
通过图再去对比上面的概念和性质,理解会更加清晰
所谓的存储结构也就数据在内存中真实的存储情况,在一维数组中
而逻辑结构就是我们想象出来的,能够帮助我们理解并且通过这个也是根据二叉树中父节点和子节点之间的下标关系来确定的
①已知父亲节点求子节点
LeftChild = Parent * 2 + 1; //左孩子的节点下标
RightChild = Parent * 2 + 2; //右孩子的节点下标
②已知子节点求父节点
Parent = (Child - 1) / 2; //切记是减1之后再除以2
向上调整算法
向上调整算法主要在堆的插入和堆排序中应用最为广泛
算法分析
对于堆的插入,就是在数组的末尾进行数字的插入,并且在插入数据之后,我们仍要保证现有的结构仍然是一个堆!

如上图,是一个小堆
然后在数组的末尾插入了一个数字,即最后一个孩子节点,但是在插入之后,我们自身的堆结构发生了变化,所以我们必须对堆的结构进行调整.
不难发现,在最后插入一个数之后,其他子树仍然保持了小堆的性质(即父节点的值小于子节点),而正在需要调整的就是该子节点的’祖宗’这条线路,如上图红色箭头一步一步指向的位置,
而利用的公式就是Parent = (Child - 1) / 2;把新插入的数和它的父节点作比较,如果这个新插入的数小于于父节点,那么就和父节点交换位置
在向上调整代码中,我们需要传入的参数是数组和插入的那个子孩子的节点的下标
void AdjustUp(HeapDataType* a, int child) //child是下标
在实际的不断向上调整中,我们需要用循环来实现代码,并且要合理的设置循环
while (child > 0) //不能设置为parent >= 0 { //Parent = (Child - 1) / 2, 通过这个公式因为parent永远都不可能小于零...}
时间复杂度 -------O(logN)
根据最坏情况来看(比如上图),数据多少层,我们就需要调整多少次,所以次数=高度h
再根据二叉树节点数量和高度的关系可知:
所以可以得到关系: 次数 = h = logN
所以时间复杂度就为:O(logN)
代码整体实现
算法既可以实现小堆也可以大堆,具体看你函数内部符号的控制
整体实现如下:
typedef struct HeapNode
{HeapDataType* a;int size;int capacity;
}HP;
void Swap(HeapDataType* p1, HeapDataType* p2)
{HeapDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//循环写法
void AdjustUp(HeapDataType* a, int child) //child,parent是下标
{int parent = (child - 1) / 2;while (child > 0){//小堆:判断子节点和父亲结点的大小if (a[child] < a[parent])//大堆:if (a[child] > a[parent]){Swap(&a[child], &a[parent]);//交换孩子和父亲child = parent;parent = (child - 1) / 2;}else{break;}}
}//递归写法
void AdjustUp(HeapDataType* a, int child)
{int parent = (child - 1) / 2;if (child > 0){//小堆:if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;AdjustUp(a, child); //递归}else{return;}}else{return;}
}
向下调整算法
向上调整算法主要在堆的数据删除和堆排序中应用最为广泛
算法分析
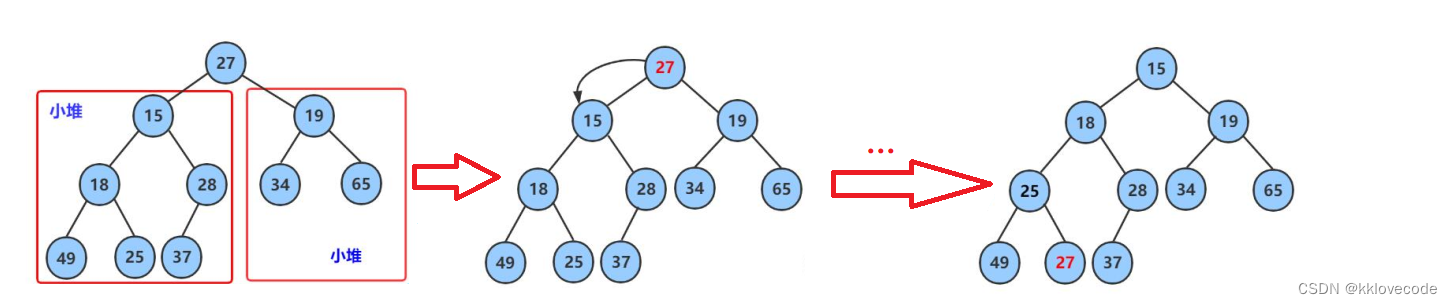
对于上图根节点27来说,它的左右子树都是小堆,所以就需要将27不断向下调整,保证其整体还是一个小堆
由此可见,向下调整的前提是左右子树必须是堆
利用的公式就是
LeftChild = Parent * 2 + 1;
RightChild = Parent * 2 + 2;
在每一轮的调整中你都需要比较左右子节点的大小,比如上图就是对于27来说,15和17两个节点,15更小,所以就将15和27进行交换,然后对于19这个子树来说本身就是一个小堆,就可以不用管了,并且15本身也小于19,所以也符合小堆性质,然后继续对左边的子树进行如此的调整
在向下调整代码中,我们需要传入的参数是数组,数组大小和整棵树根节点的下标
void AdjustDown(HeapDataType* a, int size, int parent)
时间复杂度 -------O(logN)
根据最坏情况来看(比如上图),数据多少层,最坏的情况我们就需要向下调整多少次,所以次数=高度h, 再根据二叉树节点数量和高度的关系可知:
所以可以得到关系: 次数 = h = logN
所以时间复杂度就为:O(logN)
整体代码实现
typedef int HeapDataType;typedef struct HeapNode
{HeapDataType* a;int size;int capacity;
}HP;
//转换
void Swap(HeapDataType* p1, HeapDataType* p2)
{HeapDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//循环写法
void AdjustDown(HeapDataType* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size)//这里的child是左孩子下标,之所以不是child+1<size,是因为{ //如果没有右孩子的话,这次循环将会终止,调整就会进行不彻底//小堆:if (child + 1 < size && a[child + 1] < a[child]){child++;}//小堆:if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;//交换位置}else{break;}}
}
//递归写法
void AdjustDown(HeapDataType* a, int size, int parent)
{int child = parent * 2 + 1;if (child < size) {//小堆:if (child + 1 < size && a[child + 1] < a[child]){child++; //如果右孩子小,那么下标就换成右孩子的下标}//小堆:if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;AdjustDown(a, size, parent); //递归}else{return;}}else{return;}
}
堆的接口实现
接下里,我将把堆的实现过程一步一步实现出来
初始化堆
void HeapInit(HP* hp)
{assert(hp);hp->a = NULL;hp->size = 0;hp->capacity = 0;
}
销毁堆
void HeapDestroy(HP* hp)
{assert(hp);free(hp->a);hp->a = NULL;hp->size = hp->capacity = 0;
}
插入元素
在尾部插入之后,要用
AdjustUp函数向上调整形成堆
void HeapPush(HP* hp, HPDataType x)
{assert(hp);// 扩容if (hp->size == hp->capacity){int new = hp->capacity == 0 ? 4 : hp->capacity * 2;HPDataType*tmp=(HPDataType*)realloc(hp->a, sizeof(HPDataType) * new);if (tmp == NULL){perror("realloc fail");exit(-1);}hp->a = tmp;hp->capacity = new;}hp->a[hp->size] = x;hp->size++;AdjustUp(hp->a, hp->size - 1);//插入之后向上调整堆
}
删除元素
一般指删除首元素,至于为什么HeapPop是删除首元素
根本就是因为要弹出尾元素很简单,直接size–不就完了
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);//首元素换到尾部来,然后再size----php->size;AdjustDown(php->a, php->size, 0);//再用AdjustDown函数再来调整堆
}
打印元素
void HeapPrint(HP* php)
{assert(php);for (size_t i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}
判断是否为空
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}取首元素
HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}
实现堆
int main()
{HP hp;HeapInit(&hp);int a[] = { 20, 11, 28, 31, 111, 52, 34, 16, 7, 9 };for (int i = 0; i < sizeof(a) / sizeof(int); i++){HeapPush(&hp, a[i]);//插入}HeapPop(&hp);//把堆的首元素7删除删除HeapPrint(&hp);printf("堆顶元素:%d\n", HeapTop(&hp));HeapDestroy(&hp);return 0;
}
运行出来的结果:
堆排序
首先堆排有几个关键的步骤
①创建堆 ②调整堆
创建堆
创建堆的方式有两种①向上调整建堆 ②向下调整建堆
①首先我们来看第一种:向上调整建堆
这种方式的原理就是看作最开始堆中只有一个元素,从第一个元素开始就已经在向上调整,然后逐渐像堆中加入元素,随着一个一个元素的加入,也就形成了堆
图解如下:

而代码就是通过AdjustUp函数和一个for循环就可以完成上面步骤
//以前n个数建小堆
for (int i = 0; i < n; ++i)
{AdjustUp(a, i); //a为数组的指针
}
时间复杂度: O(n*logn)
分析:首先我们上面详细分析了AdjustUp()的时间复杂度为O(logn),然后循环了n此每次建堆,所以两者相乘,时间复杂度也就是 n*logn 了
②我们来看第一种:向下调整建堆 -----堆排序中最主要用到的方法
这种建堆的关键就是从倒数第一个非叶子节点开始调(也就是树中最后一个父节点),然后逐渐+1,就可以调整从最后一个父节点开始的每一棵树.
不难发现这样也符合向下调整的前提,即左右子树都是堆
那么我们如何找到最后一个节点的父亲?
就需要用到公式:Parent = (Child - 1) / 2;
图解如下

而代码就是通过AdjustDown函数和一个for循环就可以完成上面步骤
for (int i = ((n-1)-1)/2; i >= 0; --i)
//(n-1)是拿到树最后一个节点,然后再根据公式Parent = (Child - 1) / 2;
{AdjustDown(a, size, i);
}
时间复杂度:O(n)
根据下面的思路


因此建堆的时间复杂度为O(n)
总结😗:其实两种方式建堆之所以时间复杂度有差距,就是因为向下调整建堆可以看作忽略了最后一排的节点,直接从倒数第二排节点开始调整的,而在一棵满二叉树中最后一排的节点其实就占据了整棵树的二分之一,所以相当于向下调整比向上调整少经历了很多的节点
所以实际堆排序中我们更多的使用的是向下调整建堆,因此时间复杂度为O(n)
还有一点需要注意的是:如果你想要
升序,即从小打大,需要建大堆.
建了大堆之后,再交换首元素(最大的)和末尾元素,然后把最大的元素不算入堆中的元素,
再进行向下调整
如果你建小堆,当你拿到首元素(最小的元素之后),需要将数组依次前移然后重新建堆,每次都前移然后每次都建堆,时间复杂度直接拉满!!!
同理 如果你想要降序,即从大打小,需要建小堆.
调整堆
在堆建好之后,就可以开始调整堆了,比如你是升序,即从小打大,需要建大堆.
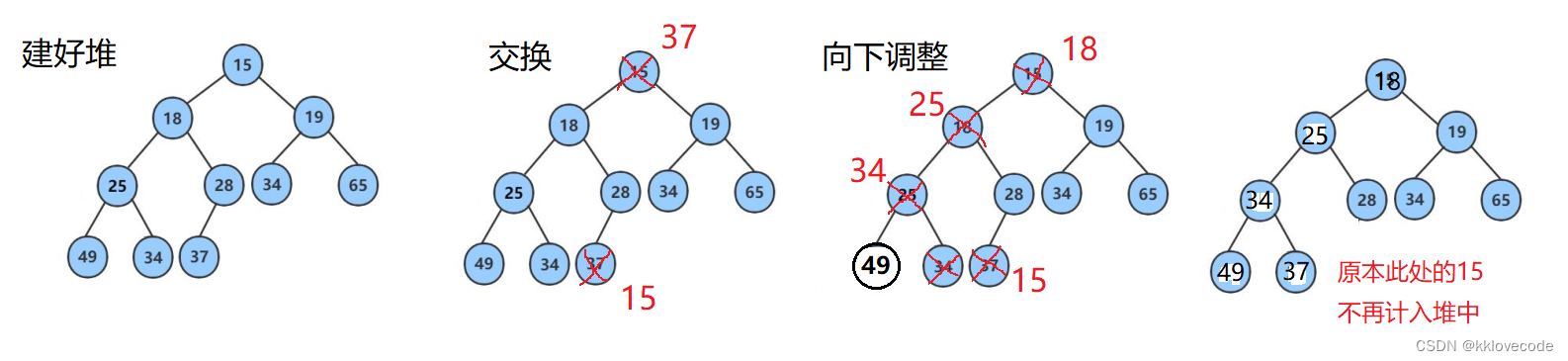
建了大堆之后,循环N次 ,进行N次调整堆操作,每一次调整 堆得到的最大值,将此值和数组的最后一个元素进行交换,交换减小数组的长度(最后被减小的那几个值不参与堆的调整),直到最后一个元素,就完成了堆的排序.
如下图,降序—小堆, 展示了其中一个调整过程
整合步骤
综合建堆和调整,完整的堆排序代码就出来了
void HeapSort(int* a, int n)
{// 建堆 (大堆)or (小堆)for (int i = 1; i < n; i++){AdjustUp(a, i);}
int end = n - 1;
while (end > 0)
{Swap(&a[0], &a[end]); //交换AdjustDown(a, end, 0); //向下调整--end; //换下来的最后一个数不计入堆中
}
升序建大堆,降序建小堆很重要!
TopK问题
最后我们再来解决一个堆在实际应用中很重要的Topk问题
通常这是在数据很大的情况下才会使用到的,如世界前500强,全省高考前十等等…
因为如果数据很大,你不可能在内存中创建一个这么大的数组来装下这么多数据,所以就要用topk问题的思路
举个简单的例子:
比如你有1000个数据,你要找前100个大的数据,那么你先随便拿100个数据(无论其大小多少)建小堆,然后另外900个数据依次与堆顶的最小数据进行比较,比它大就替换,然后再调整堆,这样1000个数据都参与了对比,对比了900次,900个最小的被拿走,剩下的100个一定是最大的,再进行堆排序
接下来用文件传输数据的形式进行举例
void CreateNDate()
{// 造数据int n = 10000000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; ++i){int x = (rand() + i) % 10000000;fprintf(fin, "%d\n", x);}fclose(fin);
}void TestTopK(const char* filename, int k)
{// 1. 建堆--用a中前k个元素建堆FILE* fout = fopen(filename, "r");if (fout == NULL){perror("fopen fail");return;}int* minheap = (int*)malloc(sizeof(int) * k);if (minheap == NULL){perror("malloc fail");return;}for (int i = 0; i < k; i++){fscanf(fout, "%d", &minheap[i]);}// 前k个数建小堆for (int i = (k-2)/2; i >=0 ; --i){AdjustDown(minheap, k, i);}// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换int x = 0;while (fscanf(fout, "%d", &x) != EOF){if (x > minheap[0]){// 替换你进堆minheap[0] = x;AdjustDown(minheap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}printf("\n");fclose(fout);
}int main()
{CreateNDate();TestTopK("data.txt", 5);return 0;
}
相关文章:

【数据结构】长篇详解堆,堆的向上/向下调整算法,堆排序及TopK问题
文章目录 堆的概念性质图解 向上调整算法算法分析代码整体实现 向下调整算法算法分析整体代码实现 堆的接口实现初始化堆销毁堆插入元素删除元素打印元素判断是否为空取首元素实现堆 堆排序创建堆调整堆整合步骤 TopK问题 堆的概念 堆就是将一组数据所有元素按完全二叉树的顺序…...

DAQ高频量化平台:引领Ai高频量化交易模式变革
近年来,数字货币投资市场掀起了一股热潮,以(BTC)为代表的区块链技术带来了巨大的商业变革。数字资产的特点,如无国界、无阶级、无门槛、高流动性和高透明度,吸引了越来越多的人们的关注和认可,创…...

vue3 element plus获取el-cascader级联选择器选中的当前结点的label值 附vue2获取当前label
各位大佬,有时我们在处理级联选择组件数据时,不仅需要拿到id,还需要拿到label名称,但是通常组件直接绑定的是id,所以就需要我们用别的方法去拿到label,此处官方是有这个方法的,具体根据不同的element 版本进行分别处理。 VUE3 e…...
Spring Boot常见面试题
Spring Boot简介 Spring Boot 是由 Pivotal 团队提供,用来简化 Spring 应用创建、开发、部署的框架。它提供了丰富的Spring模块化支持,可以帮助开发者更轻松快捷地构建出企业级应用。Spring Boot通过自动配置功能,降低了复杂性,同…...

分块矩阵求逆
另可参考Block matrix on Wikipedia2018.4.3 补充补充两个参考文献,都是对工科很实用的矩阵手册:D. S. Bernstein, Matrix mathematics: Theory, facts, and formulas with application to linear systems theory. Princeton, NJ: Princeton University …...
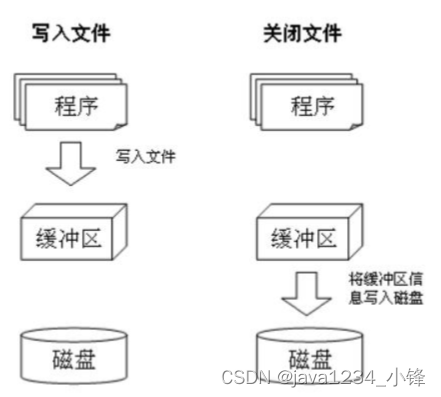
Python 文件写入操作
视频版教程 Python3零基础7天入门实战视频教程 w模式是写入,通过write方法写入内容。 # 打开文件 模式w写入,文件不存在,则自动创建 f open("D:/测试3.txt", "w", encoding"UTF-8")# write写入操作 内容写入…...

【Spring Boot系列】- Spring Boot侦听器Listener
【Spring Boot系列】- Spring Boot侦听器Listener 文章目录 【Spring Boot系列】- Spring Boot侦听器Listener一、概述二、监听器Listener分类2.1 监听ServletContext的事件监听器2.2 监听HttpSeesion的事件监听器2.3 监听ServletRequest的事件监听器 三、SpringMVC中的监听器3…...
JavaScript速成课—事件处理
目录 一.事件类型 1.窗口事件 2.表单元素事件 3.图像事件 4.键盘事件 5.鼠标事件 二.JavaScript事件处理的基本机制 三.绑定事件的方法 1.DOM元素绑定 2.JavaScript代码绑定事件 3.监听事件函数绑定 四.JavaScript事件的event对象 1.获取event对象 2.鼠标坐标获取…...
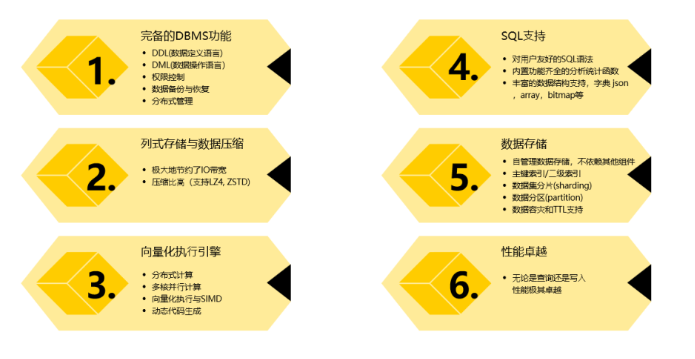
【入门篇】ClickHouse最优秀的开源列式存储数据库
文章目录 一、什么是ClickHouse?OLAP场景的关键特征列式数据库更适合OLAP场景的原因输入/输出CPU 1.1 ClickHouse的定义与发展历程1.2 ClickHouse的版本介绍 二、ClickHouse的主要特性2.1 高性能的列式存储2.2 实时的分析查询2.3 高度可扩展性2.4 数据压缩2.5 SQL支…...

【C++ Exceptions】异常处理的成本
最低成本 exception是C的一部分,编译器必须支持。即使从未使用任何异常处理机制,也必须付出一些空间放置某些数据结构,付出一些时间随时保持那些数据结构的正确性。 第二种成本:来自try语句块 避免非必要的try语句块。 粗略估计&a…...

API接口:原理、实现及应用
API(Application Programming Interface)接口是现代软件开发中不可或缺的一部分。它们提供了一种机制,使得不同的应用程序和服务可以相互通信,共享数据和功能。在这篇文章中,我们将探讨API接口的原理、实现及应用&…...
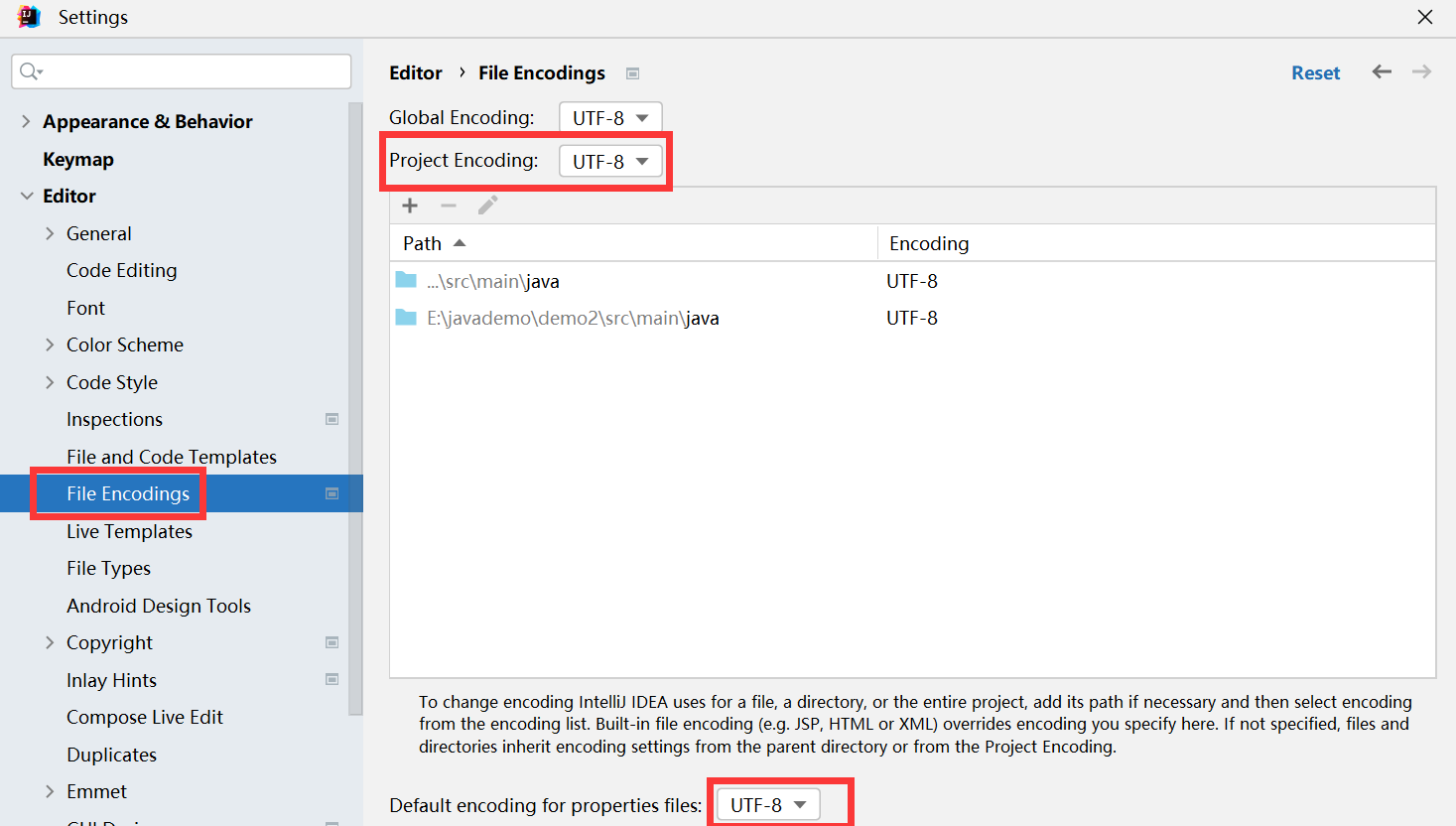
SpringBoot学习笔记(项目创建,yaml,多环境开发,整合mybatis SMM)
一、SpringBoot入门 1.1 SpringBoot概述 SpringBoot是由Pivotal团队提供的全新框架,其设计目的是用来简化Spring应用的初始搭建以及开发过程。 Spring程序缺点:配置繁琐,依赖设置繁琐。SpringBoot程序优点:自动装配,…...

Linux内核分析:输入输出,字符与块设备 31-35
CPU 并不直接和设备打交道,它们中间有一个叫作设备控制器(Device Control Unit)的组件,例如硬盘有磁盘控制器、USB 有 USB 控制器、显示器有视频控制器等。这些控制器就像代理商一样,它们知道如何应对硬盘、鼠标、键盘、显示器的行为。 输入输出设备我们大致可以分为两类…...

Linux抓包工具tcpdump
一、介绍 tcpdump是一个抓包工具,用于实时捕获和分析网络流量。它通常在unix和linux操作系统上使用。tcpdump能够捕获流经网络接口的数据包,并显示或保存它们以供进一步分析。它提供有关每个数据包的详细信息,包括源IP地址、目标IP地址、使用…...

Qt消息机制和事件
事件 事件是由Qt或者系统在不同时刻发出的,当敲下鼠标,或者按下键盘,或者当窗口需要重新绘制的时候,就会发出一个相应的事件,一些操作由用户的操作发出,一些则由系统自动发出,如系统定时器事件等。 Qt 中所有事件类都继承于 QEvent。 在事件对象创建完毕后, Qt 将这个…...

LeetCode-739-每日温度-单调栈
题目描述:给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。 题目…...
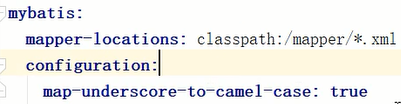
MyBatis中当实体类中的属性名和表中的字段名不一样,怎么办
方法1: 在mybatis核心配置文件中指定,springboot加载mybatis核心配置文件 springboot项目的一个特点就是0配置,本来就省掉了mybatis的核心配置文件,现在又加回去算什么事,总之这种方式可行但没人这样用 具体操作&…...
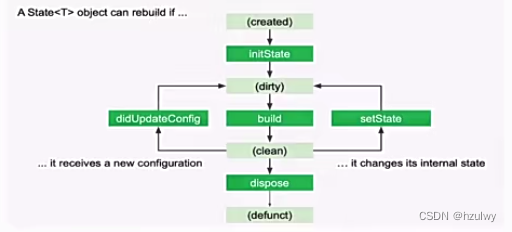
Flutter框架和原理剖析
Flutter是Google推出并开源的跨平台开发框架,主打跨平台、高保真、高性能。开发者可以通过Dart语言开发Flutter应用,一套代码同时运行在ios和Android平台。不仅如此,flutter还支持web、桌面、嵌入应用的开发。flutter提供了丰富的组件、接口&…...

NFS:使用 Ansible 自动化配置 NFS 客户端服务端
考试顺便整理博文内容整理涉及使用 Ansible 部署 NFS 客户端和服务端理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。然后在心中坚守其一生,全心全意,永不停息。所有其它的路都是不完整的,是人的逃…...
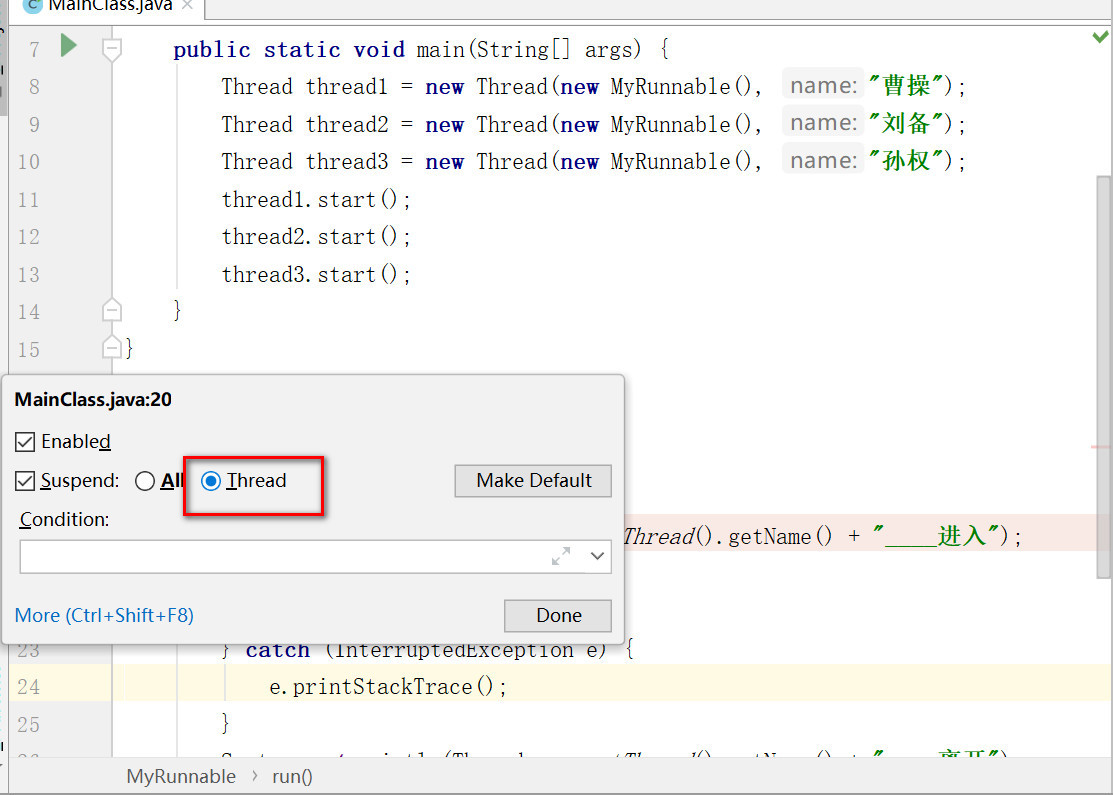
IntelliJ IDEA使用——Debug操作
文章目录 版本说明图标和快捷键查看变量计算表达式条件断点多线程调试 版本说明 当前的IntelliJ IDEA 的版本是2021.2.2(下载IntelliJ IDEA) ps:不同版本一些图标和设置位置可能会存在差异,但应该大部分都差不多。 图标和快捷键…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...
动态规划-1035.不相交的线-力扣(LeetCode)
一、题目解析 光看题目要求和例图,感觉这题好麻烦,直线不能相交啊,每个数字只属于一条连线啊等等,但我们结合题目所给的信息和例图的内容,这不就是最长公共子序列吗?,我们把最长公共子序列连线起…...