Java手写分治算法和分治算法应用拓展案例
Java手写分治算法和分治算法应用拓展案例
1. 算法思维导图
以下是用Mermanid代码表示的分治算法的实现原理:
2. 分治算法的手写必要性和市场调查
分治算法是一种高效的问题解决方法,它将问题划分为更小的子问题,然后递归地解决这些子问题,并将结果合并以得到最终解。手写分治算法的必要性在于:
- 理解算法原理:通过手写分治算法,我们可以深入理解算法的原理和逻辑,从而更好地应用于实际问题解决中。
- 提高编程能力:手写分治算法可以锻炼我们的编程能力和思维逻辑,使我们能够更好地设计和实现复杂的算法。
- 解决特定问题:分治算法在许多领域都有广泛的应用,如排序、搜索、图算法等,手写分治算法可以帮助我们解决这些特定问题。
市场调查显示,分治算法在实际应用中具有很高的市场需求和潜力。许多企业和研究机构都在寻求能够高效解决复杂问题的算法,而分治算法正是其中之一。
3. 分治算法的详细介绍和步骤
分治算法的基本思想是将一个大问题划分为若干个规模较小的子问题,然后递归地解决这些子问题,并将结果合并以得到最终解。以下是分治算法的详细步骤:
-
分解阶段:将原问题划分为若干个规模较小的子问题。这一步骤通常通过递归调用算法本身来实现。
-
解决子问题:递归地解决划分得到的子问题。当子问题的规模足够小时,可以直接求解。
-
合并解:将子问题的解合并以得到原问题的解。这一步骤通常是将子问题的解进行合并操作,得到原问题的解。
4. 分治算法的手写实现总结和思维拓展
通过手写分治算法,我们可以更好地理解和应用该算法。分治算法的手写实现总结如下:
- 理解算法原理:手写分治算法可以帮助我们理解算法的原理和逻辑,从而更好地应用于实际问题解决中。
- 提高编程能力:手写分治算法可以锻炼我们的编程能力和思维逻辑,使我们能够更好地设计和实现复杂的算法。
- 解决特定问题:分治算法在许多领域都有广泛的应用,通过手写分治算法,我们可以解决这些特定问题。
思维拓展:分治算法可以进一步扩展为并行分治算法,通过并行处理子问题来提高算法的效率和性能。
5. 分治算法的完整代码
以下是分治算法的完整代码,每行代码都附有注释:
public class DivideAndConquer {public static int divideAndConquer(int[] nums, int start, int end) {// 终止条件:当子问题规模足够小时,直接求解if (start == end) {return nums[start];}// 分解阶段:将问题划分为两个子问题int mid = (start + end) / 2;int left = divideAndConquer(nums, start, mid);int right = divideAndConquer(nums, mid + 1, end);// 合并解:将子问题的解合并int result = merge(left, right);return result;}public static int merge(int left, int right) {// 合并操作:将子问题的解进行合并return left + right;}public static void main(String[] args) {int[] nums = {1, 2, 3, 4, 5};int result = divideAndConquer(nums, 0, nums.length - 1);System.out.println("Result: " + result);}
}
6. 分治算法的应用前景调研
分治算法在许多领域都有广泛的应用前景,以下是一些应用领域的调研结果:
- 排序算法:分治算法可以用于实现高效的排序算法,如归并排序和快速排序。
- 搜索算法:分治算法可以用于实现高效的搜索算法,如二分查找和分布式搜索。
- 图算法:分治算法可以用于解决图算法中的一些问题,如最短路径和最小生成树。
7. 分治算法的拓展应用案例
以下是分治算法的三个拓展应用案例的完整代码,每个步骤都附有文字描述:
案例1:归并排序
public class MergeSort {public static void mergeSort(int[] nums, int start, int end) {if (start < end) {int mid = (start + end) / 2;mergeSort(nums, start, mid);mergeSort(nums, mid + 1, end);merge(nums, start, mid, end);}}public static void merge(int[] nums, int start, int mid, int end) {int[] temp = new int[nums.length];int i = start, j = mid + 1, k = start;while (i <= mid && j <= end) {if (nums[i] <= nums[j]) {temp[k++] = nums[i++];} else {temp[k++] = nums[j++];}}while (i <= mid) {temp[k++] = nums[i++];}while (j <= end) {temp[k++] = nums[j++];}for (i = start; i <= end; i++) {nums[i] = temp[i];}}public static void main(String[] args) {int[] nums = {5, 4, 3, 2, 1};mergeSort(nums, 0, nums.length - 1);for(int num : nums) {System.out.print(num + " ");}}
}
案例2:最大子序和
public class MaximumSubarray {public static int maxSubArray(int[] nums) {return divideAndConquer(nums, 0, nums.length - 1);}public static int divideAndConquer(int[] nums, int start, int end) {if (start == end) {return nums[start];}int mid = (start + end) / 2;int left = divideAndConquer(nums, start, mid);int right = divideAndConquer(nums, mid + 1, end);int cross = maxCrossingSubarray(nums, start, mid, end);return Math.max(Math.max(left, right), cross);}public static int maxCrossingSubarray(int[] nums, int start, int mid, int end) {int leftSum = Integer.MIN_VALUE, rightSum = Integer.MIN_VALUE;int sum = 0;for (int i = mid; i >= start; i--) {sum += nums[i];leftSum = Math.max(leftSum, sum);}sum = 0;for (int i = mid + 1; i <= end; i++) {sum += nums[i];rightSum = Math.max(rightSum, sum);}return leftSum + rightSum;}public static void main(String[] args) {int[] nums = {-2, 1, -3, 4, -1, 2, 1, -5, 4};int result = maxSubArray(nums);System.out.println("Result: " + result);}
}
案例3:汉诺塔问题
public class HanoiTower {public static void hanoi(int n, char from, char to, char temp) {if (n == 1) {System.out.println("Move disk 1 from " + from + " to " + to);return;}hanoi(n - 1, from, temp, to);System.out.println("Move disk " + n + " from " + from + " to " + to);hanoi(n - 1, temp, to, from);}public static void main(String[] args) {int n = 3;hanoi(n, 'A', 'C', 'B');}
}
8. 分治算法的拓展应用案例总结
分治算法是一种非常强大的算法思想,可以应用于解决各种问题。以下是分治算法的拓展应用案例的总结:
-
归并排序:将一个数组分成两个子数组,分别进行排序,然后将两个有序的子数组合并成一个有序的数组。归并排序的时间复杂度为O(nlogn)。
-
最大子序和:给定一个整数数组,找到一个具有最大和的连续子数组。可以使用分治算法将问题分解为三个部分:左子数组的最大子序和、右子数组的最大子序和和跨越中点的最大子序和。
-
汉诺塔问题:有三个柱子A、B、C,初始时A柱上有n个盘子,盘子大小不同,大的在下面,小的在上面。要求将所有盘子从A柱移动到C柱,并保持大小顺序不变。可以使用分治算法将问题分解为三个部分:将n-1个盘子从A柱移动到B柱,将最大的盘子从A柱移动到C柱,将n-1个盘子从B柱移动到C柱。
分治算法的拓展应用案例涵盖了排序、搜索和图算法等领域,可以帮助我们解决各种复杂的问题。通过合理地划分问题和利用子问题的解,可以提高算法的效率和准确性。因此,掌握分治算法的思想和应用是非常重要的。
相关文章:

Java手写分治算法和分治算法应用拓展案例
Java手写分治算法和分治算法应用拓展案例 1. 算法思维导图 以下是用Mermanid代码表示的分治算法的实现原理: #mermaid-svg-nvJwIm97kPHEXQOR {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-nvJwIm97kP…...

学习 CodeWhisperer 的一些总结
目前一些常见的的 AI 工具 GitHub Copilot:GitHub 与 OpenAI 合作开发的一个人工智能助手。 Codeium:是一个免费的人工智能驱动的代码生成工具 Tabnine:一个自动代码生成工具,免费版本非常有限,只提供简短的代码完成…...
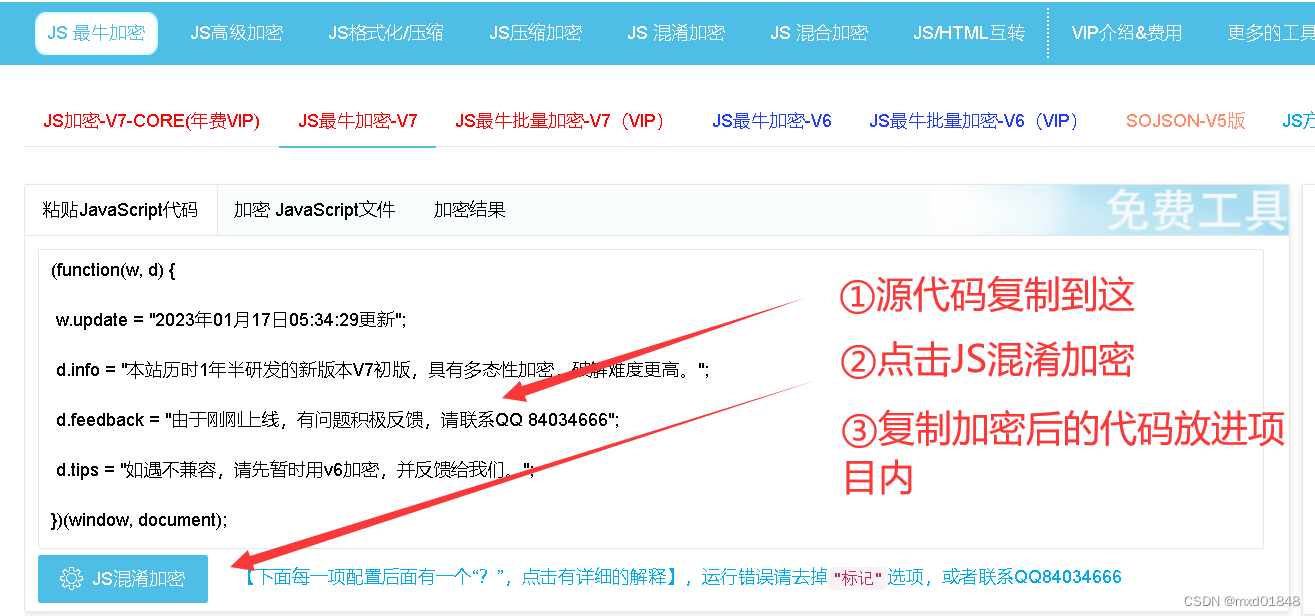
JavaScript 中的 `this` 指向问题与其在加密中的应用
JS中的 this 关键字是一个非常重要的概念,它在不同情况下会指向不同的对象或值。在本文中,我们将深入探讨 JavaScript 中 this 的各种情况,并思考如何将其应用于 JS加密中的一些有趣用途。 1. 全局上下文中的 this 在全局上下文中ÿ…...

深入理解算法的时间复杂度
文章目录 时间复杂度的定义时间复杂度的分类时间复杂度分析常见数据结构和算法的时间复杂度常见数据结构常见算法 常见排序算法说明冒泡排序(Bubble Sort)快速排序(Quick Sort)归并排序(Merge Sort)堆排序(Heap Sort) 时间复杂度的定义 时间复杂度就是一种用来描述算法在输入规…...
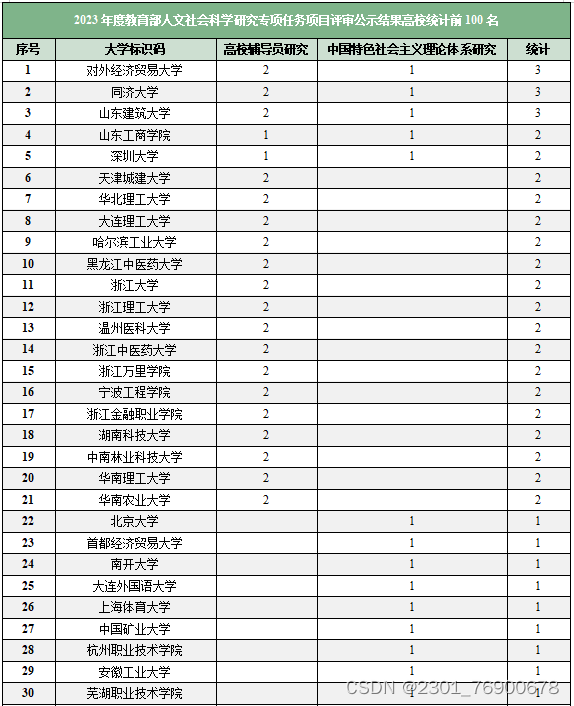
2023年度教育部人文社会科学研究一般项目评审结果,已公布!
【SciencePub学术】 9月15日,教育部社科司公示了2023年度教育部人文社会科学研究一般项目评审结果,共3482项。 其中,规划基金、青年基金、自筹经费项目共3029项通过专家评审;西部和边疆地区项目200项,新疆项目20项&a…...
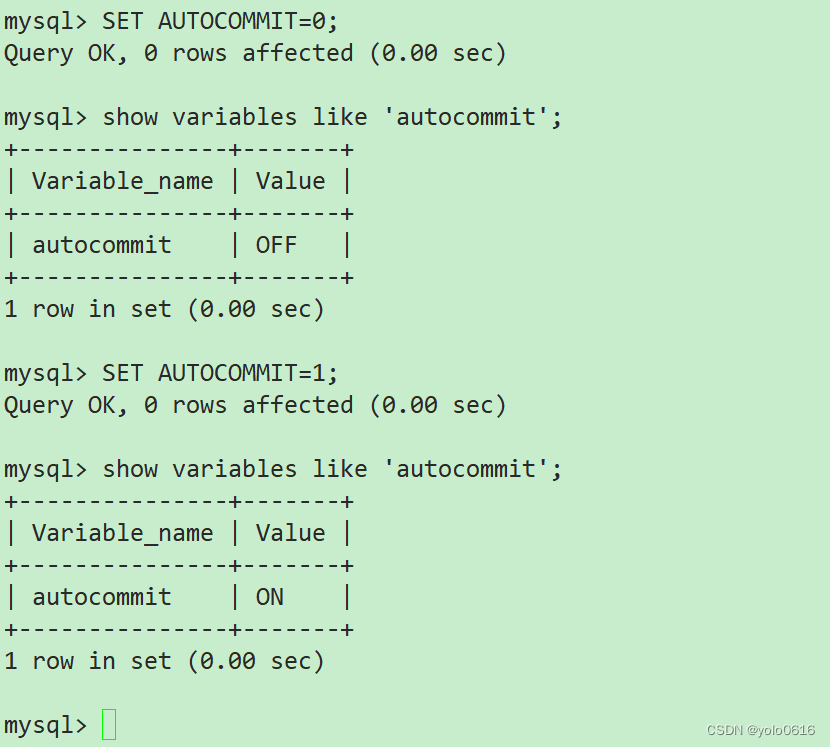
十一、MySql的事务(上)
文章目录 一、引入(一)CURD不加控制,会有什么问题?(二)CURD满足什么属性,能解决上述问题? 二、什么是事务?三、事务的特性(一)原子性:…...

时间序列分析1--生成和导出时间序列数据
时间序列数据的生成 直接录入 1.行录入 ts.(price,startc(2015,1),frequency 12) # price为时间序列变量,start为起始读入时间 frequncy指定每年读入的数据的频率,frequncy4为季度数据、frequncy52为星期数据 2.列录入 scan() 1:101 ....6:7 7:…...
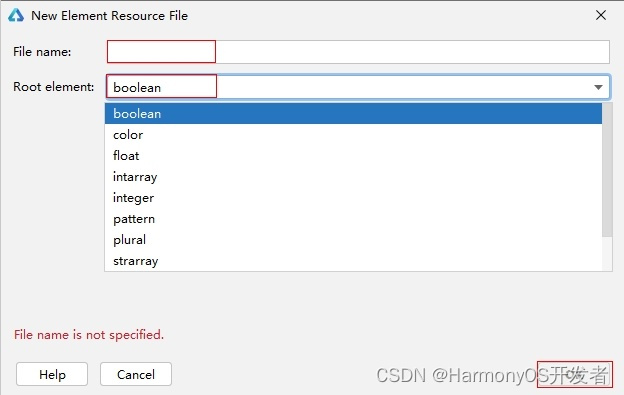
HarmonyOS应用开发—资源分类与访问
应用开发过程中,经常需要用到颜色、字体、间距、图片等资源,在不同的设备或配置中,这些资源的值可能不同。 应用资源:借助资源文件能力,开发者在应用中自定义资源,自行管理这些资源在不同的设备或配置中的表…...

C++中的转换构造函数
在 C/C++ 中,不同的数据类型之间可以相互转换。无需用户指明如何转换的称为自动类型转换(隐式类型转换),需要用户显式地指明如何转换的称为强制类型转换。 自动类型转换示例: int a = 6;a = 7.5 + a; 编译器对 7.5 是作为 double 类型处理的,在求解表达式时,先将 a 转换…...
JSP ssm 特殊人群防走失系统myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 JSP ssm 特殊人群防走失系统是一套完善的web设计系统(系统采用SSM框架进行设计开发,springspringMVCmybatis),对理解JSP java编程开发语言有帮助,系统具有完整的源 代码和数据库,系统主要…...
怎么实现一个登录时需要输入验证码的功能
今天给项目换了一个登录页面,而这个登录页面设计了验证码,于是想着把这个验证码功能实现一下吧。 这篇文章就如何实现登录时的验证码的验证功能结合代码进行详细地介绍,以及介绍功能实现的思路。 目录 页面效果 实现思路 生成验证码的控制…...

在android工程中新建Android模块报错
复制了复制正常的build.gradle文件,然后把theme里面的东西改成了下面这个样就好了 <resources xmlns:tools"http://schemas.android.com/tools"><!-- Base application theme. --><style name"Theme.JiQuan" parent"Theme…...
电脑桌面的复选框如何取消
电脑桌面图标的复选框如何取消 1. 概述2. 去掉图标的复选框方法结束语 1. 概述 当你拿到新的电脑开机后,发现桌面上软件应用的图标左上角有个小框,每次点击图标都会显示,并且点击图标时,小框还会打上√; 这个小框的…...

【Unity每日一记】资源加载相关和检测相关
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:uni…...
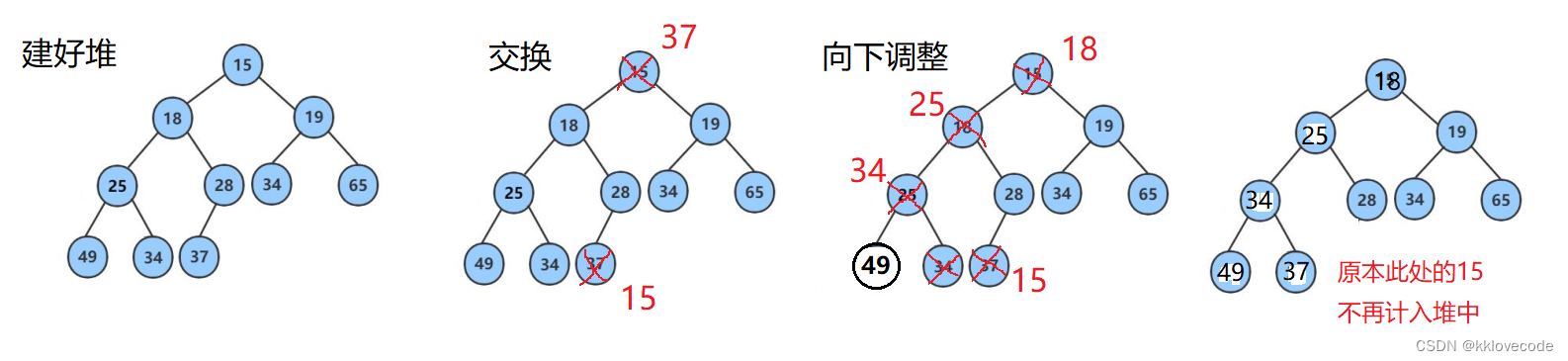
【数据结构】长篇详解堆,堆的向上/向下调整算法,堆排序及TopK问题
文章目录 堆的概念性质图解 向上调整算法算法分析代码整体实现 向下调整算法算法分析整体代码实现 堆的接口实现初始化堆销毁堆插入元素删除元素打印元素判断是否为空取首元素实现堆 堆排序创建堆调整堆整合步骤 TopK问题 堆的概念 堆就是将一组数据所有元素按完全二叉树的顺序…...

DAQ高频量化平台:引领Ai高频量化交易模式变革
近年来,数字货币投资市场掀起了一股热潮,以(BTC)为代表的区块链技术带来了巨大的商业变革。数字资产的特点,如无国界、无阶级、无门槛、高流动性和高透明度,吸引了越来越多的人们的关注和认可,创…...

vue3 element plus获取el-cascader级联选择器选中的当前结点的label值 附vue2获取当前label
各位大佬,有时我们在处理级联选择组件数据时,不仅需要拿到id,还需要拿到label名称,但是通常组件直接绑定的是id,所以就需要我们用别的方法去拿到label,此处官方是有这个方法的,具体根据不同的element 版本进行分别处理。 VUE3 e…...
Spring Boot常见面试题
Spring Boot简介 Spring Boot 是由 Pivotal 团队提供,用来简化 Spring 应用创建、开发、部署的框架。它提供了丰富的Spring模块化支持,可以帮助开发者更轻松快捷地构建出企业级应用。Spring Boot通过自动配置功能,降低了复杂性,同…...

分块矩阵求逆
另可参考Block matrix on Wikipedia2018.4.3 补充补充两个参考文献,都是对工科很实用的矩阵手册:D. S. Bernstein, Matrix mathematics: Theory, facts, and formulas with application to linear systems theory. Princeton, NJ: Princeton University …...
Python 文件写入操作
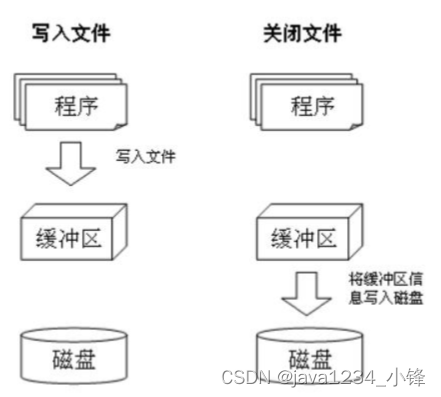
视频版教程 Python3零基础7天入门实战视频教程 w模式是写入,通过write方法写入内容。 # 打开文件 模式w写入,文件不存在,则自动创建 f open("D:/测试3.txt", "w", encoding"UTF-8")# write写入操作 内容写入…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
