代码随想录算法训练营第56天 | ● 583. 两个字符串的删除操作 ● 72. 编辑距离 ● 动态规划之编辑距离总结篇
文章目录
- 前言
- 一、583. 两个字符串的删除操作
- 二、72. 编辑距离
- 三、动态规划之编辑距离总结篇
- 总结
前言
一、583. 两个字符串的删除操作
两种思路:1.直接动态规划,求两个字符串需要删除的最小次数 2.采用子序列的和-最长公共子序列。思路一分析如下:
动规五部曲,分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
这里dp数组的定义有点点绕,大家要撸清思路。
- 确定递推公式
- 当word1[i - 1] 与 word2[j - 1]相同的时候
- 当word1[i - 1] 与 word2[j - 1]不相同的时候
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
那最后当然是取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2,所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
这里可能不少录友有点迷糊,从字面上理解 就是 当 同时删word1[i - 1]和word2[j - 1],dp[i][j-1] 本来就不考虑 word2[j - 1]了,那么我在删 word1[i - 1],是不是就达到两个元素都删除的效果,即 dp[i][j-1] + 1。
- dp数组如何初始化
从递推公式中,可以看出来,dp[i][0] 和 dp[0][j]是一定要初始化的。
dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。
- 确定遍历顺序
从递推公式 dp[i][j] = min(dp[i - 1][j - 1] + 2, min(dp[i - 1][j], dp[i][j - 1]) + 1); 和dp[i][j] = dp[i - 1][j - 1]可以看出dp[i][j]都是根据左上方、正上方、正左方推出来的。
所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
- 举例推导dp数组
代码(思路一):
关键代码:
dp[i][j] = Math.min(dp[i - 1][j - 1] + 2, Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));
优化代码:
dp[i][j] = Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
class Solution {public int minDistance(String word1, String word2) {int len1 = word1.length();int len2 = word2.length();int[][] dp = new int[len1+1][len2+1];for(int i =1;i<=len1;i++){dp[i][0] = i; }for(int j = 1;j<=len2;j++){dp[0][j] = j;}for(int i = 1;i<=len1;i++){for(int j =1;j<=len2;j++){if(word1.charAt(i-1) == word2.charAt(j-1)){dp[i][j] = dp[i-1][j-1];}else{dp[i][j] = Math.min(dp[i][j-1]+1,dp[i-1][j]+1);}}}return dp[len1][len2];}
}
代码(思路二):
class Solution {public int minDistance(String word1, String word2) {int len1 = word1.length();int len2 = word2.length();int[][] dp = new int[len1+1][len2+1];for(int i = 1;i<= len1;i++){for(int j = 1;j<= len2;j++){if(word1.charAt(i-1) == word2.charAt(j-1)){dp[i][j] = dp[i-1][j-1] +1;}else{dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);}}}return len1 + len2 - 2*dp[len1][len2];}
}二、72. 编辑距离
因为前面的铺垫,这题显得并不困难,难点在于理解;另外,本题的代码基本复制的上一题的解法一,只更改了了一行代码:
dp[i][j] = Math.min(dp[i - 1][j - 1] + 1, Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));
因为题解基本一致,这里只提及了最有差异的递推公式的解:
确定递推公式
在确定递推公式的时候,首先要考虑清楚编辑的几种操作,整理如下:
if (word1[i - 1] == word2[j - 1])不操作 if (word1[i - 1] != word2[j - 1])增删换也就是如上4种情况。
if (word1[i - 1] == word2[j - 1])那么说明不用任何编辑,dp[i][j]就应该是dp[i - 1][j - 1],即dp[i][j] = dp[i - 1][j - 1];此时可能有同学有点不明白,为啥要即
dp[i][j] = dp[i - 1][j - 1]呢?那么就在回顾上面讲过的
dp[i][j]的定义,word1[i - 1]与word2[j - 1]相等了,那么就不用编辑了,以下标i-2为结尾的字符串word1和以下标j-2为结尾的字符串word2的最近编辑距离dp[i - 1][j - 1]就是dp[i][j]了。在下面的讲解中,如果哪里看不懂,就回想一下
dp[i][j]的定义,就明白了。在整个动规的过程中,最为关键就是正确理解
dp[i][j]的定义!
if (word1[i - 1] != word2[j - 1]),此时就需要编辑了,如何编辑呢?
- 操作一:word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。
即
dp[i][j] = dp[i - 1][j] + 1;
- 操作二:word2删除一个元素,那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。
即
dp[i][j] = dp[i][j - 1] + 1;这里有同学发现了,怎么都是删除元素,添加元素去哪了。
word2添加一个元素,相当于word1删除一个元素,例如
word1 = "ad" ,word2 = "a",word1删除元素'd'和word2添加一个元素'd',变成word1="a", word2="ad", 最终的操作数是一样! dp数组如下图所示意的:a a d+-----+-----+ +-----+-----+-----+| 0 | 1 | | 0 | 1 | 2 |+-----+-----+ ===> +-----+-----+-----+a | 1 | 0 | a | 1 | 0 | 1 |+-----+-----+ +-----+-----+-----+d | 2 | 1 |+-----+-----+操作三:替换元素,
word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增删加元素。可以回顾一下,
if (word1[i - 1] == word2[j - 1])的时候我们的操作 是dp[i][j] = dp[i - 1][j - 1]对吧。那么只需要一次替换的操作,就可以让 word1[i - 1] 和 word2[j - 1] 相同。
所以
dp[i][j] = dp[i - 1][j - 1] + 1;综上,当
if (word1[i - 1] != word2[j - 1])时取最小的,即:dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;递归公式代码如下:
if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1]; } else {dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1; }
class Solution {public int minDistance(String word1, String word2) {int len1 = word1.length();int len2 = word2.length();int[][] dp = new int[len1+1][len2+1];for(int i =1;i<=len1;i++){dp[i][0] = i; }for(int j = 1;j<=len2;j++){dp[0][j] = j;}for(int i = 1;i<=len1;i++){for(int j =1;j<=len2;j++){if(word1.charAt(i-1) == word2.charAt(j-1)){dp[i][j] = dp[i-1][j-1];}else{dp[i][j] = Math.min(dp[i-1][j-1]+1,Math.min(dp[i][j-1]+1,dp[i-1][j]+1));}}}return dp[len1][len2];}
}
三、动态规划之编辑距离总结篇
考虑动态规划,首先明确dp数组以及下标的含义(如果是i-1,j-1,考虑一下好处),随后是递推公式,这里需要对两个字符串(因为基本是字符串数组)的前后操作进行思考,接着进行初始化,初始化会因为dp数组的含义不同而不同;其次是根据递推公式确定遍历顺序,因此最后一步打印dp数组也成为检验的重要一步。
总结
动态规划。
相关文章:

代码随想录算法训练营第56天 | ● 583. 两个字符串的删除操作 ● 72. 编辑距离 ● 动态规划之编辑距离总结篇
文章目录 前言一、583. 两个字符串的删除操作二、72. 编辑距离三、动态规划之编辑距离总结篇总结 前言 一、583. 两个字符串的删除操作 两种思路:1.直接动态规划,求两个字符串需要删除的最小次数 2.采用子序列的和-最长公共子序列。思路一分析如下&#…...

矩阵 m * M = c
文章目录 题1题2 题1 (2023江苏领航杯-prng) 题目来源:https://dexterjie.github.io/2023/09/12/%E8%B5%9B%E9%A2%98%E5%A4%8D%E7%8E%B0/2023%E9%A2%86%E8%88%AA%E6%9D%AF/ 题目描述: (没有原数据,自己生成的数据) from Crypto.Util.number…...

Linux——IO
✅<1>主页::我的代码爱吃辣 📃<2>知识讲解:Linux——文件系统 ☂️<3>开发环境:Centos7 💬<4>前言:是不是只有C/C有文件操作呢?python,java&…...
svn(乌龟svn)和SVN-VS2022插件(visualsvn) 下载
下载地址: https://www.visualsvn.com/visualsvn/download/...
开源日报 0824 | 构建UI组件和页面的前端工作坊
Storybook 是一个用于构建 UI 组件和页面的前端工作坊,支持多种主流框架,提供丰富的插件,具有可配置性强和扩展性好的特点。 storybookjs/storybook Stars: 79.9k License: MIT Storybook 是一个用于构建 UI 组件和页面的前端工作坊&#x…...

福建三明大型工程机械3D扫描工程零件三维建模逆向抄数-CASAIM中科广电
高精度3D扫描技术已经在大型工件制造领域发挥着重要作用,可以高精度高效率实现全尺寸三维测量,本期,我们要分享的应用是大型工程机械3D扫描案例。 铣轮是深基础施工领域内工法先进、技术复杂程度高、高附加值的地连墙设备,具有成…...
使用香橙派学习 Linux的守护进程
Q:什么是守护进程 A:Linux Daemon(守护进程)是运行在后台的一种特殊进程。它独立于控制终端并且周期性地执行 某种任务或等待处理某些发生的事件。它不需要用户输入就能运行而且提供某种服务,不是对整个系统就是对某个…...

数据治理-数据仓库和商务智能
数据仓库的作用 减少数据冗余,提高信息一致性,让企业能够利用数据做出更优决策的方法,数据仓库是企业数据管理的核心。 业务驱动因素 运营支持职能、合规需求(历史数据响应)和商务智能活动(主因࿱…...

CH2--x86系统架构概览
2.1 OVERVIEW OF THE SYSTEM-LEVEL ARCHITECTURE 图中的实线箭头表示线性地址,虚线表示段选择器,虚线箭头表示物理地址 2.1.1 Global and Local Descriptor Tables 全局描述符表 (GDT) GDT是一个全局的段描述符表,它存储在系统内存中的一个固…...

Immutable.js API 简介
Immutable-js 这个库的实现是深拷贝还是浅拷贝?immutable 来源immutable.js三大特性: 持久化数据结构结构共享惰性操作 Immutable.js 的几种数据类型 immutable 使用 使用 npm 安装 immutable: 常用API介绍 MapListList.isList() 和 Map.isMa…...
)
HLSL 入门(一)
HLSL High Level Shader Language 高级着色语言,是Direct3D中用来编写Shader的语言。其语法类似于C语言。 虽然其主要作用是用来编写例如顶点着色器,像素着色器。但本质是对图形并行管线进行编程,因此也能用来编写用于计算的着色器ÿ…...

【Docker】挂载数据卷
一、Docker数据卷说明及操作 在Docker中挂载数据卷是一种将数据持久化保存的方法,以便容器之间或容器与主机之间共享数据。以下是如何在Docker中挂载数据卷的步骤: 1、创建数据卷 首先,您需要创建一个数据卷。可以使用以下命令创建一个数据卷…...

[技术干货]spring 和spring boot区别
Spring 和 Spring Boot 都是 Java 框架,用于构建企业级应用程序。Spring 是一个完整的框架,提供各种功能,包括依赖注入、事务管理、数据访问、Web 开发等。Spring Boot 是一个基于 Spring 的框架,旨在简化 Spring 应用程序的开发和…...

【hudi】数据湖客户端运维工具Hudi-Cli实战
数据湖客户端运维工具Hudi-Cli实战 help hudi:student_mysql_cdc_hudi_fl->help AVAILABLE COMMANDSArchived Commits Commandtrigger archival: trigger archivalshow archived commits: Read commits from archived files and show detailsshow archived commit stats: …...

RK3588 添加ROOT权限
一.ROOT简介 ROOT权限是Linux和Unix系统中的超级管理员用户帐户,该帐户拥有整个系统的最高权利,可以执行几乎所有操作。ROOT就是获取安卓系统中的最高用户权限,以便执行一些需要高权限才能执行的操作(包括卸载系统自带程序、刷机、备份、还原…...
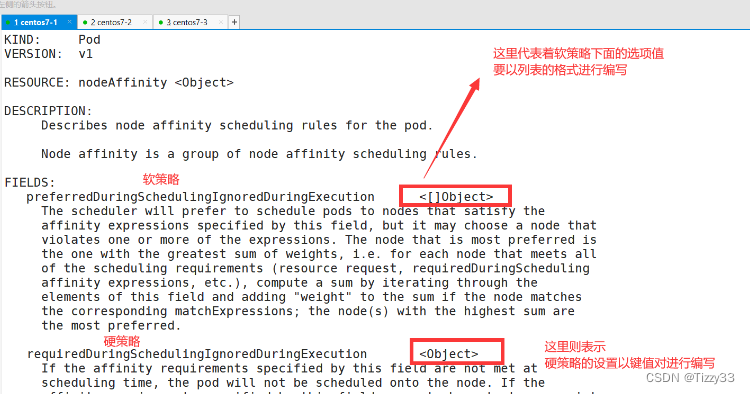
【云原生】k8s-----集群调度
目录 1.k8s的list-watch机制 1.1 list-watc机制简介 1.2 根据list-watch机制,pod的创建流程 2.scheduler的调度策略 2.1 scheduler的调度策略简介 2.2 Scheduler预选策略的算法 2.3 Scheduler优选策略的算法 3. k8s中的标签管理及nodeSelector和nodeName的 调…...
一键集成prometheus监控微服务接口平均响应时长
一、效果展示 二、环境准备 prometheus + grafana环境 参考博文:https://blog.csdn.net/luckywuxn/article/details/129475991 三、导入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter...
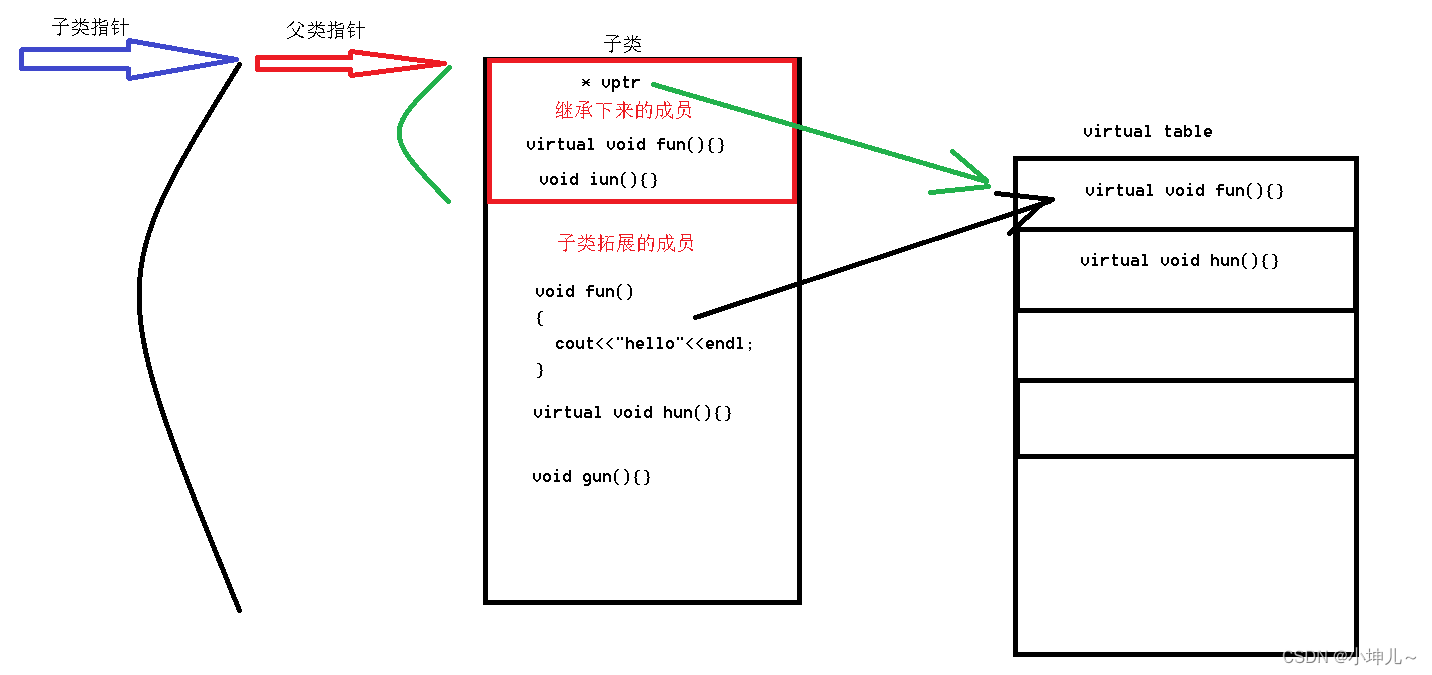
2023/9/13 -- C++/QT
作业: 1> 将之前定义的栈类和队列类都实现成模板类 栈: #include <iostream> #define MAX 40 using namespace std;template <typename T> class Stack{ private:T *data;int top; public:Stack();~Stack();Stack(const Stack &ot…...
mybatis mapper.xml转建表语句
从网上下载了代码,但是发现没有DDL建表语句,只能自己手动创建了,感觉太麻烦,就写了一个工具类 将所有的mapper.xml放入到一个文件夹中,程序会自动读取生成建表语句 依赖的jar <dependency><groupId>org.d…...

封装使用Axios进行前后端交互
Axios是一个强大的HTTP客户端,用于在Vue.js应用中进行前后端数据交互。本文将介绍如何在Vue中使用Axios,并通过一个企业应用场景来演示其实际应用。 Axios简介 公众号:Code程序人生,个人网站:https://creatorblog.cn A…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
