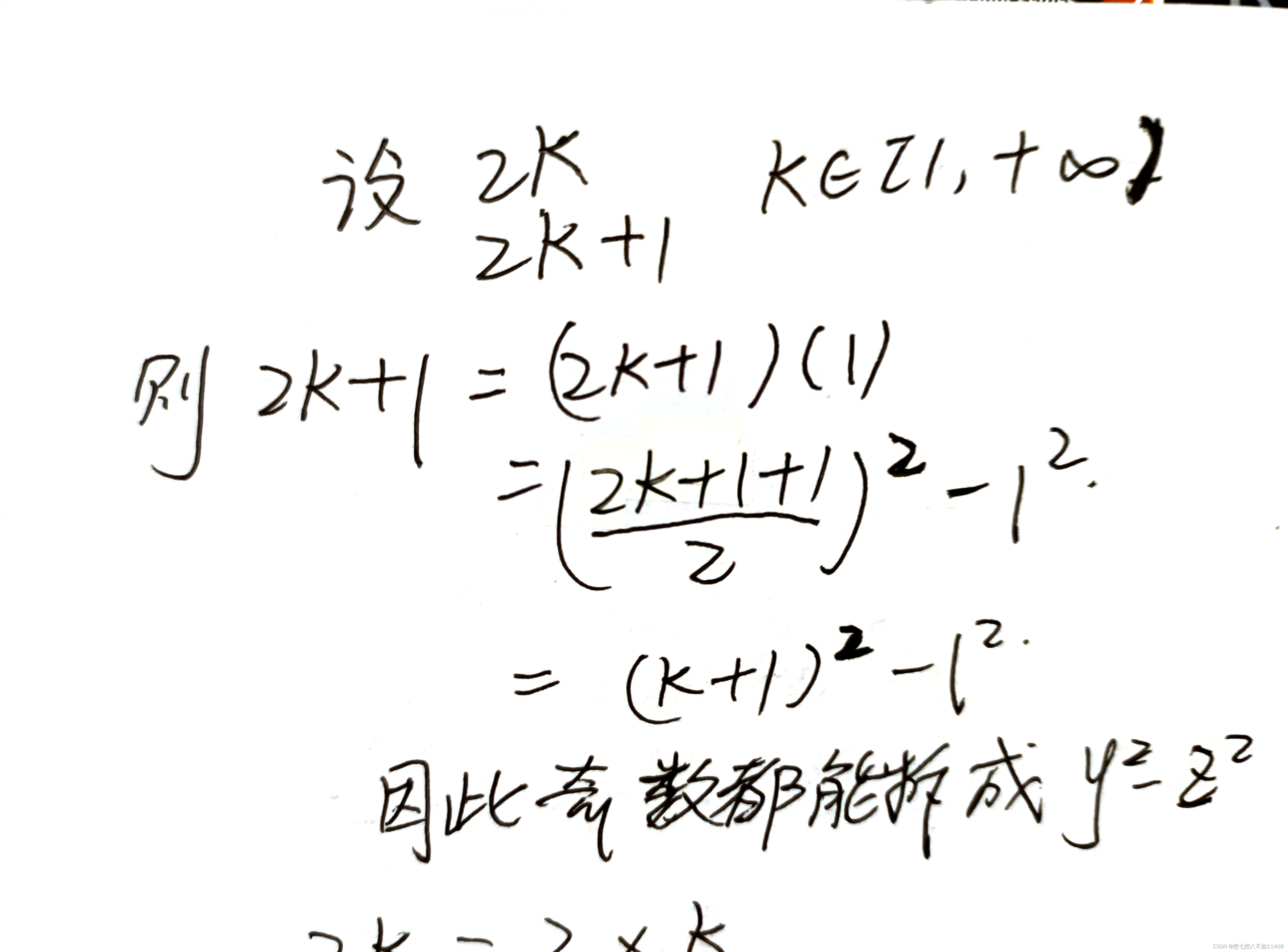【刷题】蓝桥杯
蓝桥杯2023年第十四届省赛真题-平方差 - C语言网 (dotcpp.com)
初步想法,x = y2 − z2=(y+z)(y-z)
即x=a*b,a=y+z,b=y-z
2y=a+b
即a+b是2的倍数就好了。
即x存在两个因数之和为偶数就能满足条件。
但时间是(r-l)*x,数据1e9,直接T了
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
map<int,int> mp;
int cnt;bool judge(int x)
{for(int i=1;i<=x;i++)//找两个因数 {if(x%i!=0) continue;int d=x/i+i;if(d%2==0||x==1)//说明是整数 {return true; } }return false;
}
signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int l,r;cin>>l>>r; for(int i=l;i<=r;i++){if(judge(i)) cnt++; }cout<<cnt;return 0;
}运行结果:

进一步分析:
根据题意多写几个,不难发现奇数似乎都能拆成y2 − z2的形式?因此,我们从奇偶的角度来找规律。
(这个地方写错了,是
那么,在这里就可以得出结论辣。想要数字能表示成y2-z2的形式,只有两种可能:
1.奇数 2.4的倍数
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int cnt;signed main()
{int l,r;cin>>l>>r; for(int i=l;i<=r;i++){if(i%2) cnt++;if(i%4==0) cnt++;}cout<<cnt;return 0;
}
(这一步还不能过属实有点钻牛角尖了。。。。。
但是好在,已知一个数x,对应的奇数、4的倍数的数的个数是可以算出来的。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int cnt;
signed main()
{int l,r;cin>>l>>r; int d=(l-1)/2;if((l-1)%2==0) d--;int p=l/4;if((l%4)==0) p--;cnt=(r-1)/2-d+r/4-p;cout<<cnt;return 0;
}相关文章:

【刷题】蓝桥杯
蓝桥杯2023年第十四届省赛真题-平方差 - C语言网 (dotcpp.com) 初步想法,x y2 − z2(yz)(y-z) 即xa*b,ayz,by-z 2yab 即ab是2的倍数就好了。 即x存在两个因数之和为偶数就能满足条件。 但时间是(r-l)*x&am…...

C++入门及简单例子_4
1. 类和对象: #include <iostream> // 包含输入输出流库的头文件class Rectangle { // 定义名为Rectangle的类 private: // 私有成员变量部分double length; // 长度double width; // 宽度public: // 公有成员函数部分Rectangle(double len, double w…...

成集云 | 用友U8集成聚水潭ERP(用友U8主管库存)| 解决方案
源系统成集云目标系统 方案介绍 用友U8是一套企业级的解决方案,可满足不同的制造、商务模式下,不同运营模式下的企业经营管理。它全面集成了财务、生产制造及供应链的成熟应用,并延伸客户管理至客户关系管理(CRM)&am…...
提升网站效率与SEO优化:ZBlog插件集成解决方案
在创建和管理网站的过程中,使用合适的工具和插件可以大幅提升效率,并改善搜索引擎优化(SEO)结果。ZBlog插件是为ZBlogCMS设计的一组工具,它们帮助网站管理员轻松地满足各种需求,从采集内容到发布、推送和SE…...
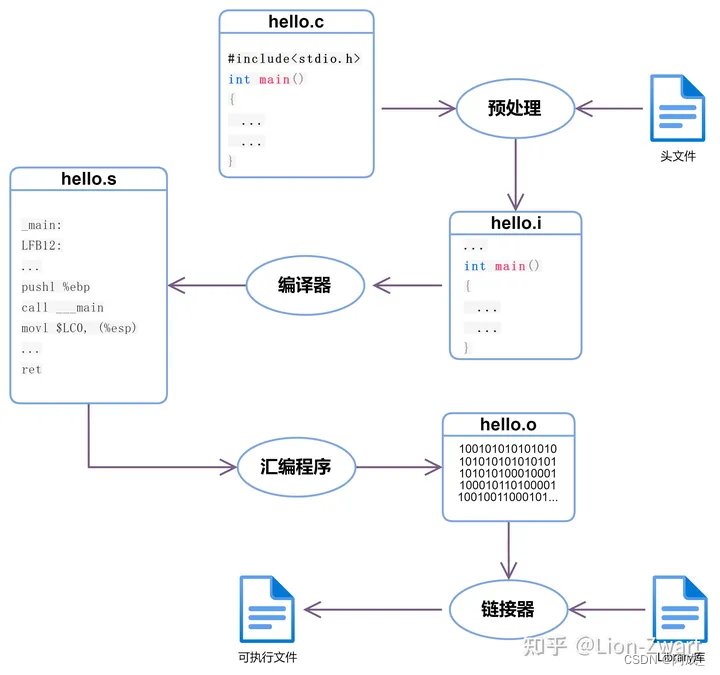
C语言的编译过程详解
当我们编译C程序时会发生什么?编译过程中的组件有哪些,编译执行过程是什么样的? 什么是编译 C语言的编译过程就是把我们可以理解的高级语言代码转换为计算机可以理解的机器代码的过程,其实就是一个翻译的过程。 …...

无人机航测没信号?北斗卫星来解决
无人机航测是利用无人机进行地理信息的采集和处理的航测方式。相比传统的航测手段,无人机航测具备更高的灵活性、更低的成本和更广阔的适应性。无人机航测可以应用于土地测绘、农业植保、城市规划、自然资源调查等多个领域,极大地提高了测绘的效率和准确…...

Vue 03 数据绑定
Vue中有2种数据绑定的方式: 1.单向绑定(v-bind): 数据只能从data流向页面。 2.双向绑定(v-model): 数据不仅能从data流向页面,还可以从页面流向data。 备注: 1.双向绑定一般都应用在表单类元素上(如&am…...
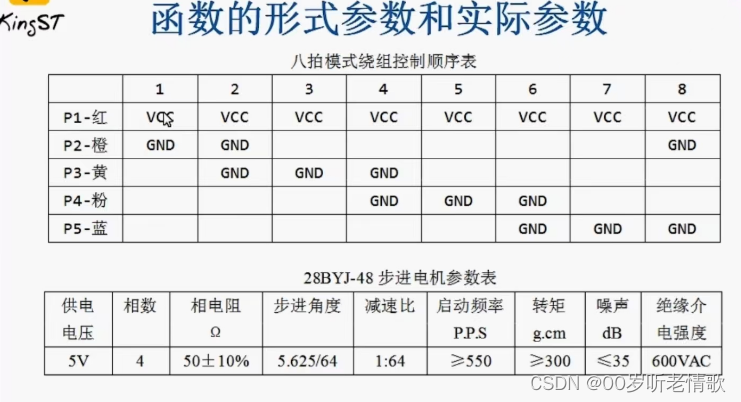
#循循渐进学51单片机#步进电机与蜂鸣器#not.8
1、能够理解清楚单片机IO口的结构。 2)t1相当于PnP三级管,t2相当于npn三极管 3) 强推挽io具有较强的驱动能力,电流输出能力很强。 2、能够看懂上下拉电阻的电路应用,并且熟练使用上下拉电阻。 3、理解28BYJ-48减速步进电机的工作…...
计算存储是不是智算时代的杀手锏?
想象一下,在一个繁忙的数据中心里,有一家大型互联网公司叫做“数据中心的故事”。这家公司一直在使用传统的CPU架构来处理海量数据。但是随着数据量的不断增长,CPU架构遇到了很多问题和瓶颈,这让“数据中心的故事”感到非常苦恼。…...
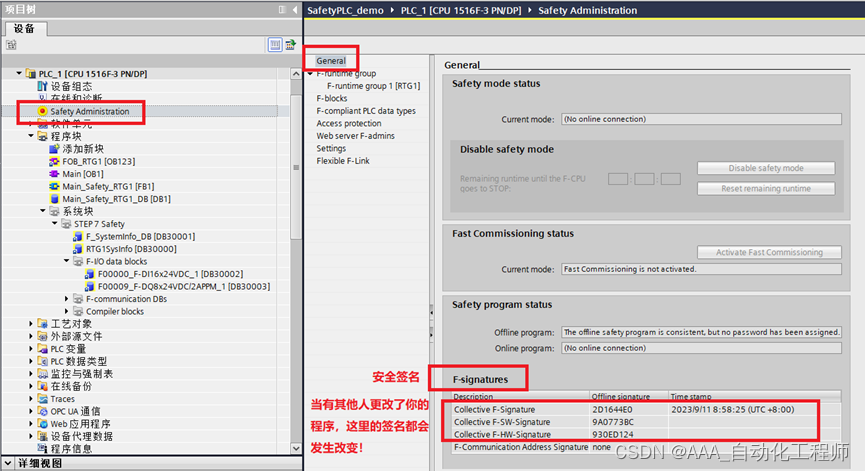
西门子S7-1200F或1500F系列安全PLC的组态步骤和基础编程(二)
西门子S7-1200F或1500F系列安全PLC的组态步骤和基础编程(二) 上一次和大家分享了组态相关的重要内容,具体可以参考以下链接中的内容: 西门子S7-1200F或1500F系列安全PLC的组态步骤和基础编程(一) 本次继续和大家分享关于安全PLC基础编程的相关内容: 如下图所示,在左侧的…...

【Spring Boot】Spring Boot中的简单查询
前面介绍了在Spring Boot项目中集成JPA框架,实现数据的增、删、改、查等功能。Spring Data JPA的使用非常简单,只需继承JpaRepository即可实现完整的数据操作方法,无须任何数据访问层和SQL语句。JPA除了这些功能和优势之外,还有非…...

Transformer 01(自注意机制Self-attention)
一、Self-attention [台大李宏毅] 1.1 向量序列的输入 一个序列作为输入: 多个向量输入举例: 一个句子: 声音信号: 图: 1.2 输出 二、Sequence labeling 输入与输出一样多:Sequence labeling 窗口开的…...

交流共享,共筑智算底座丨九州未来受邀出席英特尔线下沙龙
随着AI技术的升级迭代、生成式AI模型智能化水平的持续提升,AIGC加速向多种场景渗透,AIGC迎来应用爆发期,有望实现且跨越更多领域的融合,形成新的应用场景和解决方案,持续推动数字技术的创新与应用,助力各行…...

【EI会议信息】第五届土木建筑与城市工程国际学术会议(ICCAUE 2023)
第五届土木建筑与城市工程国际学术会议(ICCAUE 2023) 2023 5th International Conference on Civil Architecture and Urban Engineering (ICCAUE 2023) 第五届土木建筑与城市工程国际学术会议(ICCAUE 2023)由天津大学主办&…...

上海亚商投顾:沪指震荡反弹 汽车产业链全天强势
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 一.市场情绪 大小指数昨日集体反弹,沪指3100点失而复得,创业板指一度涨超1.5%,随后涨幅…...

【Python深度学习】深度学习入门介绍
引言 深度学习是人工智能领域中最受关注和研究的子领域之一,它在计算机视觉、自然语言处理、语音识别、推荐系统等各个领域都有广泛的应用。本文将详细介绍深度学习的发展历史、不同类型、应用领域以及未来发展前景。 1、深度学习的发展历史 深度学习的起源可以追溯…...

【Linux系统编程】进程概念与基本创建
文章目录 1. 进程的概念2. 进程描述—PCB3. task_struct—PCB的一种4. task_ struct内容分类5. 查看进程 这篇文章我们来学习下一个概念——进程 1. 进程的概念 那什么是进程呢,我们该如何理解它呢? 如果我们打开电脑的任务管理: 我们看到这…...

webpack:详解CopyWebpackPlugin,复制的同时修改文件内容
摘要 CopyWebpackPlugin 是一个强大的 Webpack 插件,用于将文件从源目录复制到构建目录。在本文中,我们将探讨 CopyWebpackPlugin 的一些常用 API,并提供示例代码。 在构建 Web 应用程序时,通常需要将一些静态文件(如…...

Twin-Builder—系统级多物理域数字孪生平台
Twin Builder是ANSYS公司系统仿真业务的核心产品,是一款跨学科多领域系统仿真软件和数字孪生平台。能够实现复杂系统的建模、仿真和验证,基于IIoT物联网平台对数字孪生体进行集成、部署与运行,在完成复杂系统功能、性能的验证和优化的同时&am…...

用selenium和xpath定位元素并获取属性值以及str字符型转json型
页面html如图所示: 要使用xpath定位这个div元素,并且获取其属性data-config的内容值。 from selenium import webdriver from selenium.webdriver.common.by import By from selenium.webdriver.chrome.options import Optionshost127.0.0.1 port10808 …...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...