MYSQL索引——B+树讲解
B-/B+树看 MySQL索引结构
B-树
B-树,这里的 B 表示 balance( 平衡的意思),B-树是一种多路自平衡的搜索树.它类似普通的平衡二叉树,不同的一点是B-树允许每个节点有更多的子节点。下图是 B-树的简化图.

B-树有如下特点:
所有键值分布在整颗树中;
任何一个关键字出现且只出现在一个结点中;
搜索有可能在非叶子结点结束;
在关键字全集内做一次查找,性能逼近二分查找;
B+ 树
B+树是B-树的变体,也是一种多路搜索树, 它与 B- 树的不同之处在于:
所有关键字存储在叶子节点出现,内部节点(非叶子节点并不存储真正的 data)
为所有叶子结点增加了一个链指针
简化 B+树 如下图

为什么使用B-/B+ Tree
红黑树等数据结构也可以用来实现索引,但是文件系统及数据库系统普遍采用B-/+Tree作为索引结构。MySQL 是基于磁盘的数据库系统,索引往往以索引文件的形式存储的磁盘上,索引查找过程中就要产生磁盘I/O消耗,相对于内存存取,I/O存取的消耗要高几个数量级,索引的结构组织要尽量减少查找过程中磁盘I/O的存取次数。为什么使用B-/+Tree,还跟磁盘存取原理有关。
局部性原理与磁盘预读
由于磁盘的存取速度与内存之间鸿沟,为了提高效率,要尽量减少磁盘I/O.磁盘往往不是严格按需读取,而是每次都会预读,磁盘读取完需要的数据,会顺序向后读一定长度的数据放入内存。而这样做的理论依据是计算机科学中著名的局部性原理:
当一个数据被用到时,其附近的数据也通常会马上被使用
程序运行期间所需要的数据通常比较集中
由于磁盘顺序读取的效率很高(不需要寻道时间,只需很少的旋转时间),因此对于具有局部性的程序来说,预读可以提高I/O效率.预读的长度一般为页(page)的整倍数。
MySQL(默认使用InnoDB引擎),将记录按照页的方式进行管理**,每页大小默认为16K(这个值可以修改)**.linux 默认页大小为4K
B-/+Tree索引的性能分析
实际实现B-Tree还需要使用如下技巧:
每次新建节点时,直接申请一个页的空间,这样就保证一个节点物理上也存储在一个页里,加之计算机存储分配都是按页对齐的,就实现了一个结点只需一次I/O。
假设 B-Tree 的高度为 h,B-Tree中一次检索最多需要h-1次I/O(根节点常驻内存),渐进复杂度为O(h)=O(logdN)O(h)=O(logdN)。一般实际应用中,出度d是非常大的数字,通常超过100,因此h非常小(通常不超过3)。
而红黑树这种结构,h明显要深的多。由于逻辑上很近的节点(父子)物理上可能很远,无法利用局部性,所以红黑树的I/O渐进复杂度也为O(h),效率明显比B-Tree差很多。
B-Tree和B+Tree中为什么优先选择B+Tree
B+树更适合外部存储,由于内节点无 data 域,一个结点可以存储更多的内结点,每个节点能索引的范围更大更精确,也意味着 B+树单次磁盘IO的信息量大于B-树,I/O效率更高。
Mysql是一种关系型数据库,区间访问是常见的一种情况,B+树叶节点增加的指向相邻节点的链指针,加强了区间访问性,可使用在范围区间查询等,而B-树每个节点 key 和 data 在一起,则无法区间查找(between, <,>)。
B+Tree的定义
B+Tree是B树的变种,有着比B树更高的查询性能,来看下m阶B+Tree特征:
有m个子树的节点包含有m个元素(B-Tree中是m-1)
根节点和分支节点中不保存数据,只用于索引,所有数据都保存在叶子节点中。
所有分支节点和根节点都同时存在于子节点中,在子节点元素中是最大或者最小的元素。
叶子节点会包含所有的关键字,以及指向数据记录的指针,并且叶子节点本身是根据关键字的大小从小到大顺序链接。

红点表示是指向卫星数据的指针,指针指向的是存放实际数据的磁盘页,卫星数据就是数据库中一条数据记录。
叶子节点中还有一个指向下一个叶子节点的next指针,所以叶子节点形成了一个有序的链表,方便遍历B+树。
B+树的优势
1.更加高效的单元素查找
B+树的查找元素3的过程:
第一次磁盘IO

第二次磁盘IO

第三次磁盘IO

这个过程看下来,貌似与B树的查询过程没有什么区别。但实际上有两点不一样:
a、首先B+树的中间节点不存储卫星数据,所以同样大小的磁盘页可以容纳更多的节点元素,如此一来,相同数量的数据下,B+树就相对来说要更加矮胖些,磁盘IO的次数更少。
b、由于只有叶子节点才保存卫星数据,B+树每次查询都要到叶子节点;而B树每次查询则不一样,最好的情况是根节点,最坏的情况是叶子节点,没有B+树稳定。
2.叶子节点形成有顺链表,范围查找性能更优
B树范围查找3-8的过程
a、先查找3

b、再查找4、5、6、7、8,中间过程省略,直接到8的查找

这里查找的范围跨度越大,则磁盘IO的次数越多,性能越差。
B+树范围查找3-11的过程

先从上到下找到下限元素3,然后通过链表指针,依次遍历得到元素5/6/8/9/11;如此一来,就不用像B树那样一个个元素进行查找。
总结
1.单节点可以存储更多的元素,使得查询磁盘IO次数更少。
2.所有查询都要查找到叶子节点,查询性能稳定。
3.所有叶子节点形成有序链表,便于范围查询。
PS:在数据库的聚集索引(Clustered Index)中,叶子节点直接包含卫星数据。在非聚集索引(NonClustered Index)中,叶子节点带有指向卫星数据的指针。
相关文章:

MYSQL索引——B+树讲解
B-/B树看 MySQL索引结构 B-树 B-树,这里的 B 表示 balance( 平衡的意思),B-树是一种多路自平衡的搜索树.它类似普通的平衡二叉树,不同的一点是B-树允许每个节点有更多的子节点。下图是 B-树的简化图. B-树有如下特点: 所有键值分布在整颗树中; 任何一…...
VB将十进制整数转换成16进制以内的任意进制数
VB将十进制整数转换成16进制以内的任意进制数 数值转换,能够将十进制整数转换成16进制以内的任意进制数 Private Function DecToN(ByVal x%, ByVal n%) As StringDim p() As String, y$, r%p Split("0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F", ",")I…...

基于SpringBoot+Vue的宠物领养饲养交流管理平台设计与实现
前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 👇🏻…...
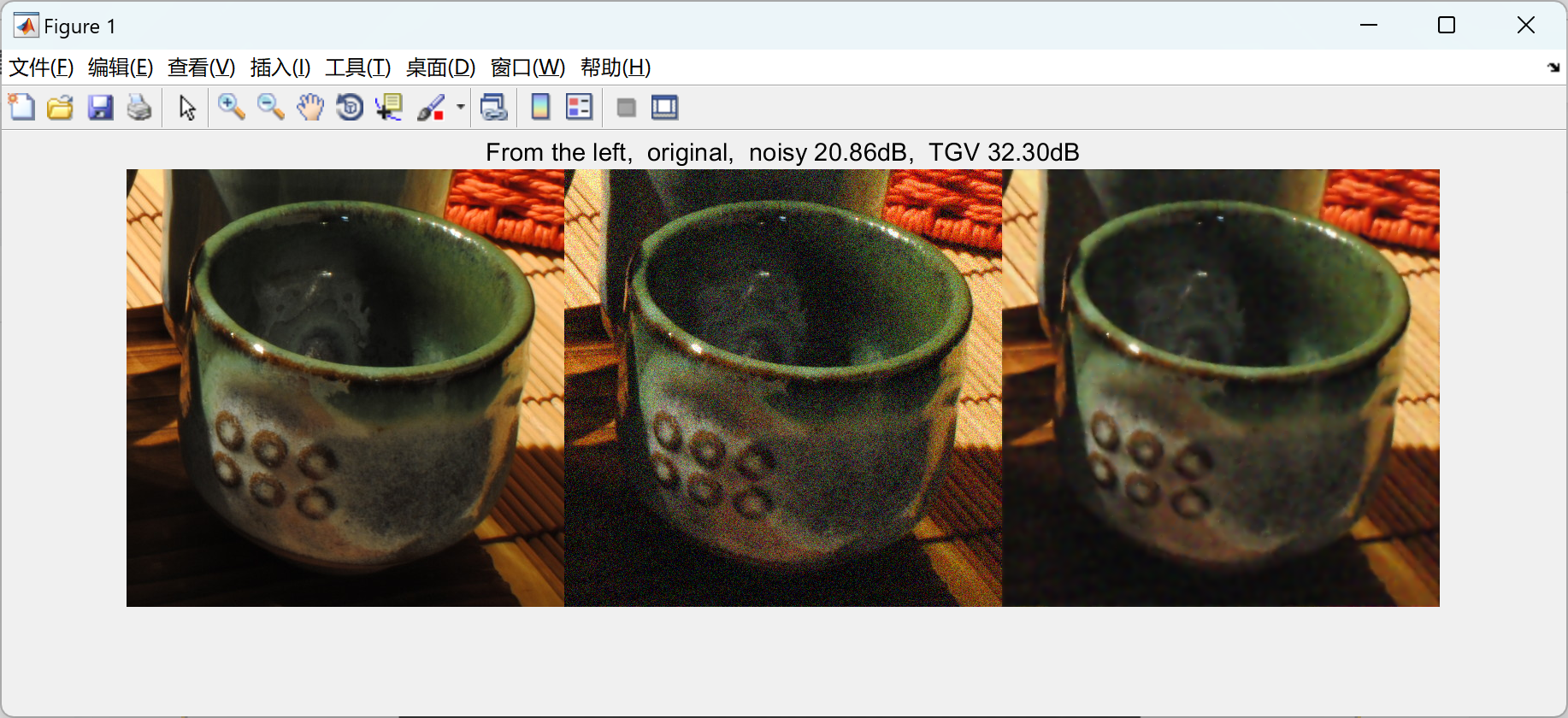
【图像去噪】【TGV 正则器的快速计算方法】通过FFT的总(广义)变化进行图像去噪(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

windbg调试句柄问题
这里写自定义目录标题 winform,句柄资源不够强,程序crash句柄主程序c程序,加载的插件是c# dll,这时候如何用windbg调试dll库如果查看句柄和对象的关系!handle 怎么能知道哪个句柄是Form对话框的句柄如何查看句柄对应的类对象 winf…...
9月13-14日上课内容 第三章 ELK日志分析系统及部署实例
本章结构 ELK日志分析系统简介 ELK日志分析系统分为 Elasticsearch Logstash Kibana 日志处理步骤 1.将日志进行集中化管理 2.将日志格式化(Logstash) 并输出到Elasticsearch 3.对格式化后的数据进行索引和存储 (Elasticsearch) 4.前端数据的展示(Kibana) Elasticsearch介…...

服务器端应用的安装
前言:相信看到这篇文章的小伙伴都或多或少有一些编程基础,懂得一些linux的基本命令了吧,本篇文章将带领大家服务器如何部署一个使用django框架开发的一个网站进行云服务器端的部署。 文章使用到的的工具 Python:一种编程语言&…...

关于硬盘质量大数据分析的思考
近日,看到Backblaze分享了一遍关于硬盘运行监控数据架构的文章,觉得挺有意义的,本文就针对这方面跟大家聊聊。 作为一家在2021年在美国纳斯达克上市的云端备份公司,Backblaze一直保持着对外定期发布HDD和SSD的故障率稳定性质量报告…...
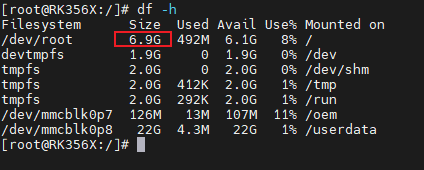
RK3568核心板分区空间不足,如何修改分区大小?
在对评估板进行开发验证时,时常会遇到根目录空间不足的情况,而在其他分区又有冗余空间,这时则需要对分区大小重新进行分配,合理化利用分区空间。 本文将基于HD-RK3568-IOT评估板主要讲解如何修改eMMC分区大小。 1. 分区表介绍…...
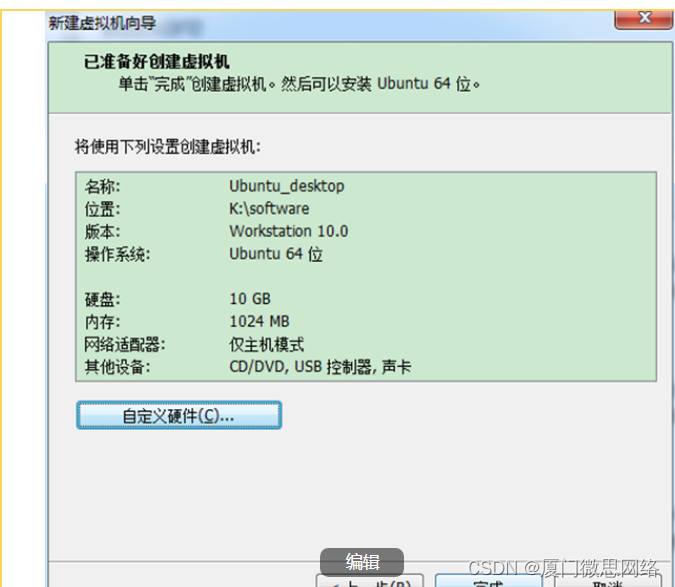
Linux系统怎么修改主机名
【微|信|公|众|号:厦门微思网络】 1.备份主机名文件 首先redhat修改主机名,在进行任何修改之前,请务必备份主机名文件。这样,即使出现意外情况,你也能够轻松恢复到原始状态。使用以下命令备份主机名文件࿱…...

BroadcastChannel方法跨浏览器窗口通信
1. 描述 同源 的不同浏览器窗口,Tab 页,frame 或者 iframe 下的不同文档之间可以通过 BroadcastChannel 相互通信。 2. 构造函数 通过 BroadcastChannel 类传入的参数创建实例,传入的参数将指定通道名称,在同源环境下该通道可以…...
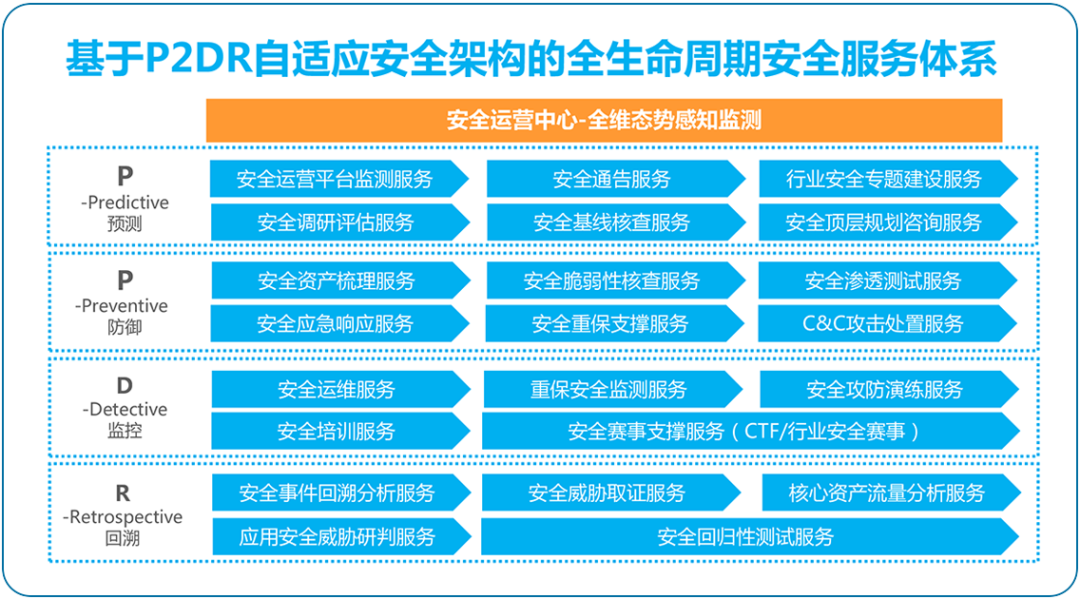
山石网科国产化防火墙,打造全方位边界安全解决方案
互联网的快速发展促进了各行各业的信息化建设,但也随之带来了诸多网络安全风险。大部分组织机构采用统一互联网接入方案,互联网出口承担着内部用户访问互联网的统一出口和对外信息服务的入口,因此在该区域部署相匹配的安全防护手段必不可少。…...
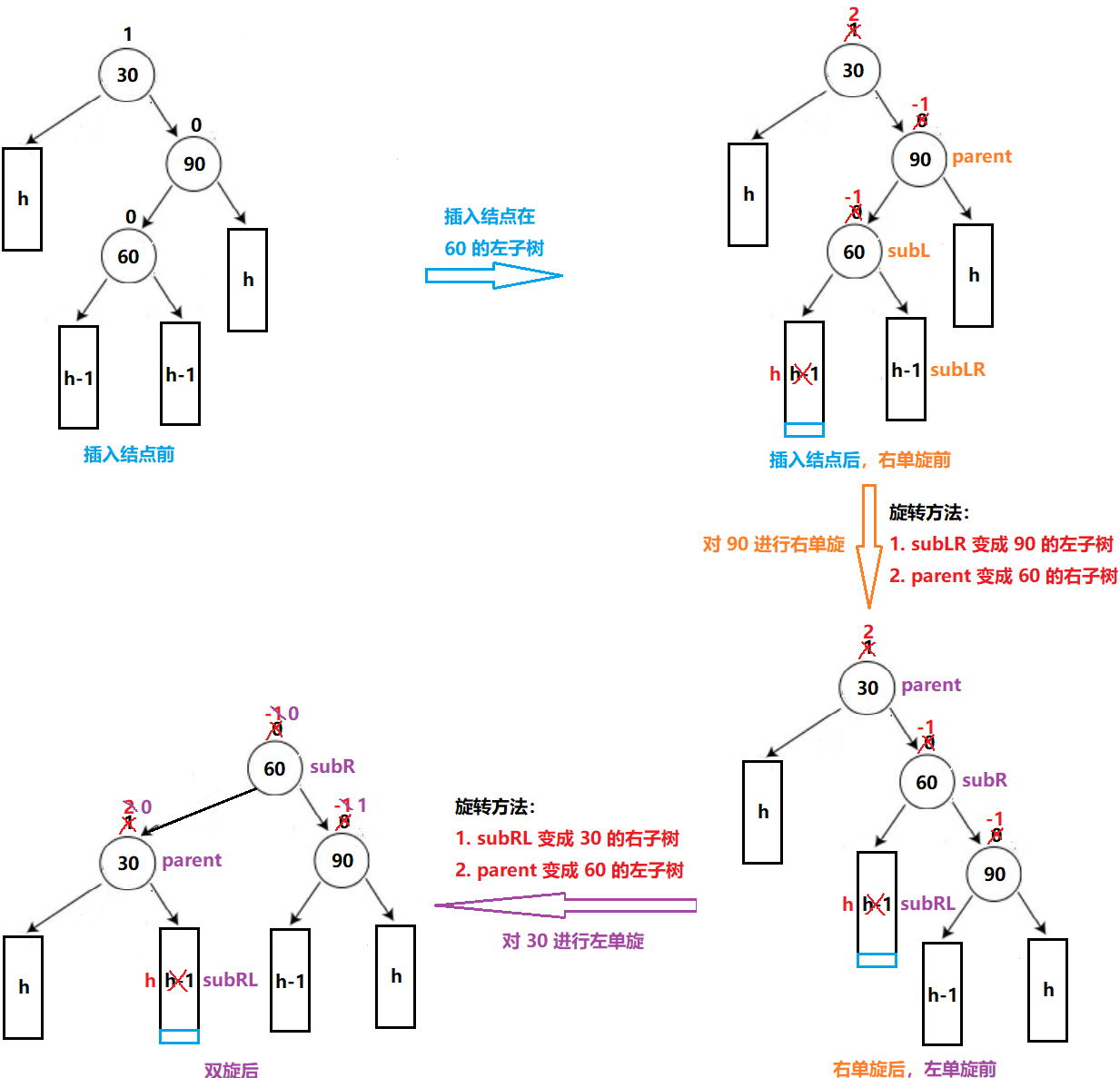
AVL 树
文章目录 一、AVL 树的概念二、AVL 树的实现1. AVL 树的存储结构2. AVL 树的插入 一、AVL 树的概念 在 二叉搜索树 中,当我们连续插入有序的数据时,二叉搜索树可能会呈现单枝树的情况,此时二叉搜索树的查找效率为 O(N) 俄罗斯的两位数学家 …...
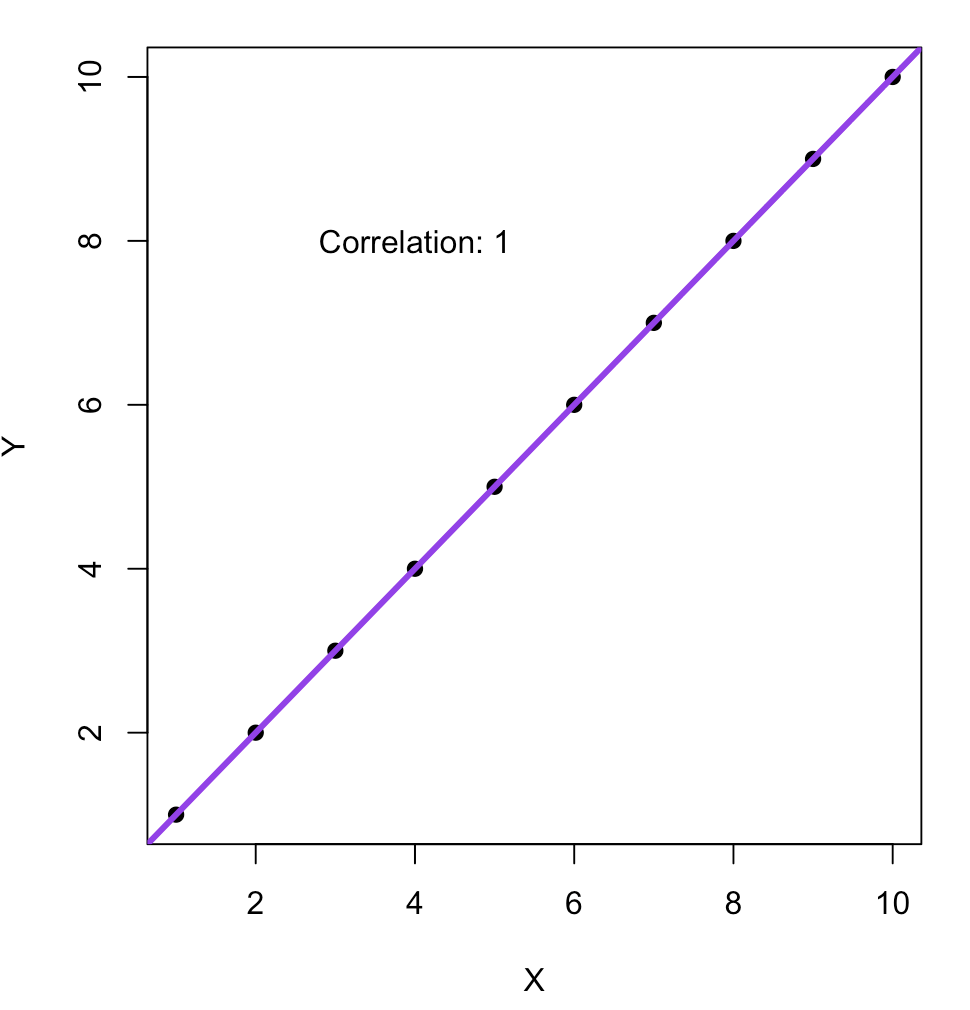
ggplot2做图(填坑中)
数据 df <- data.frame(x 1:10, y 1:10, f c(rep("A", 5), rep("B", 5))) 做图 1. 散点图 (scatter plot) # scatter plot scatter_plot <- function(df, metadata) {identical(rownames(df), rownames(metadata))data <- cbind(df, metada…...
Python日志处理器,同时打印到控制台和保存到文件中,并保证格式一致
使用logging模块的时候,默认是输出到控制台的,当然也可以配置输出到文件中,但是当你配置了文件后,控制台的输出就消失了,所以,需要一个策略即能保存到文件中,又能输出到控制台中。 下面是我做的…...
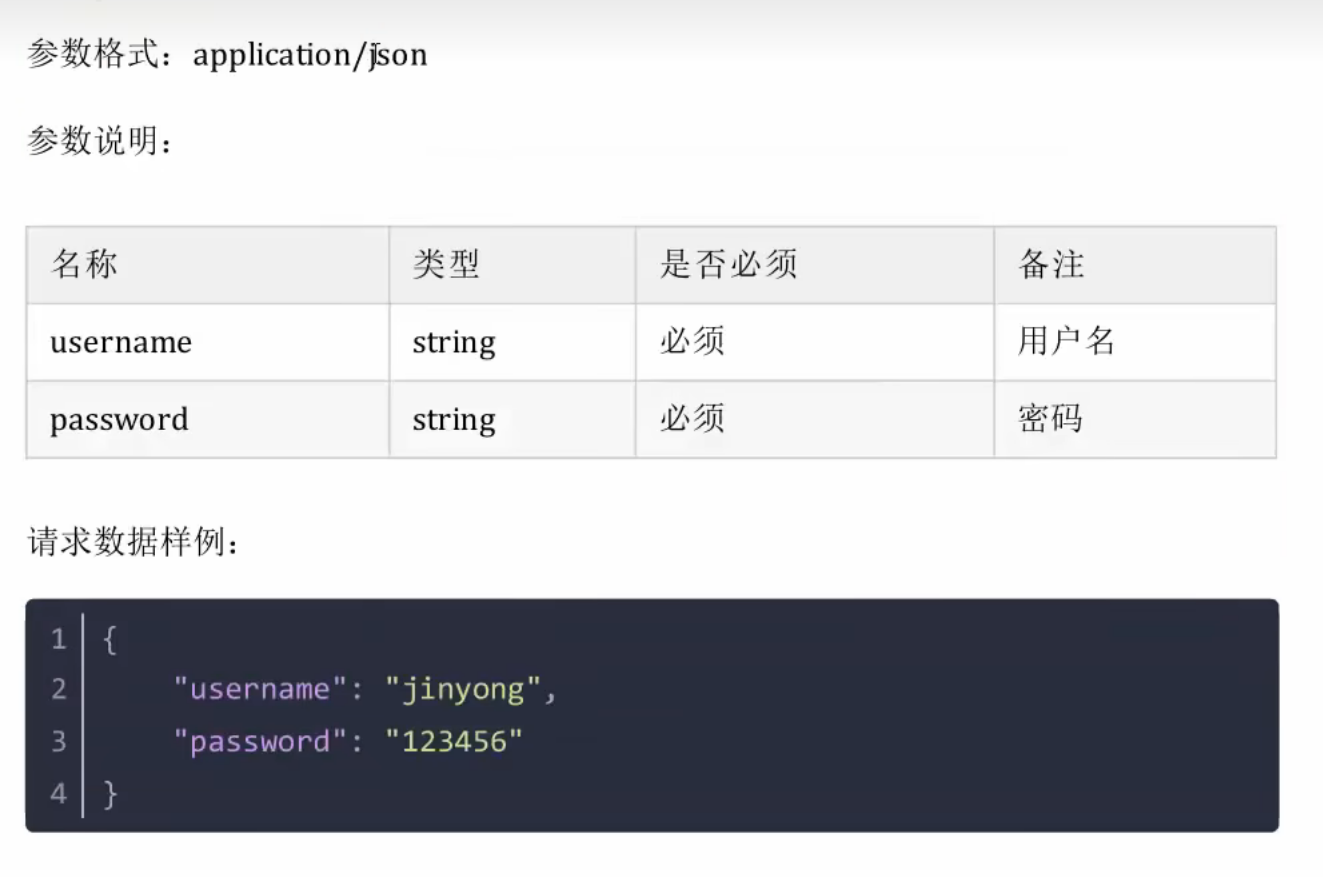
JavaWeb后端开发登录操作 登录功能 通用模板/SpringBoot整合
登录功能的思路 前端会传入两个参数:用户名和密码 在用户表中查询用户名,并校对相应的密码(涉及查询操作) SQL语句 select * from emp where username jingyong and password 123456; 如果有则成功,没有则登录失败.不可能为多个,因为添加了unique唯一约束,最终只会有一条 …...

The 2023 ICPC Asia Regionals Online Contest (1)(A D I J K L)
The 2023 ICPC Asia Regionals Online Contest (1)(A D I J K L) PTA | 程序设计类实验辅助教学平台 A Qualifiers Ranking Rules(模拟) 考虑先对第一场和第二场分别去重(取最好) , 归并排序后再次去重即可。 #include<bits/stdc.h> using namespace std;…...

C++ PrimerPlus 复习 第七章 函数——C++的编程模块(上)
第一章 命令编译链接文件 make文件 第二章 进入c 第三章 处理数据 第四章 复合类型 (上) 第四章 复合类型 (下) 第五章 循环和关系表达式 第六章 分支语句和逻辑运算符 第七章 函数——C的编程模块(上ÿ…...
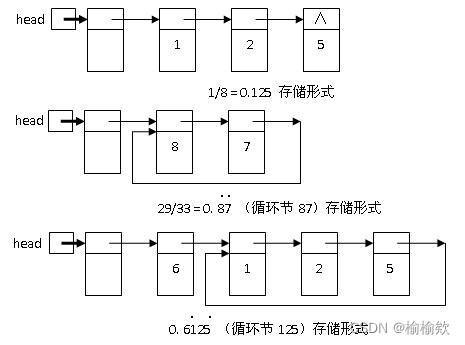
2.求循环小数
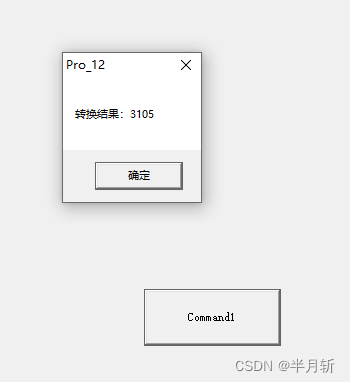
题目 对于任意的真分数 N/M ( 0 < N < M ),均可以求出对应的小数。如果采用链表表示各个小数,对于循环节采用循环链表表示,则所有分数均可以表示为如下链表形式。 输入: N M 输出: 转换…...
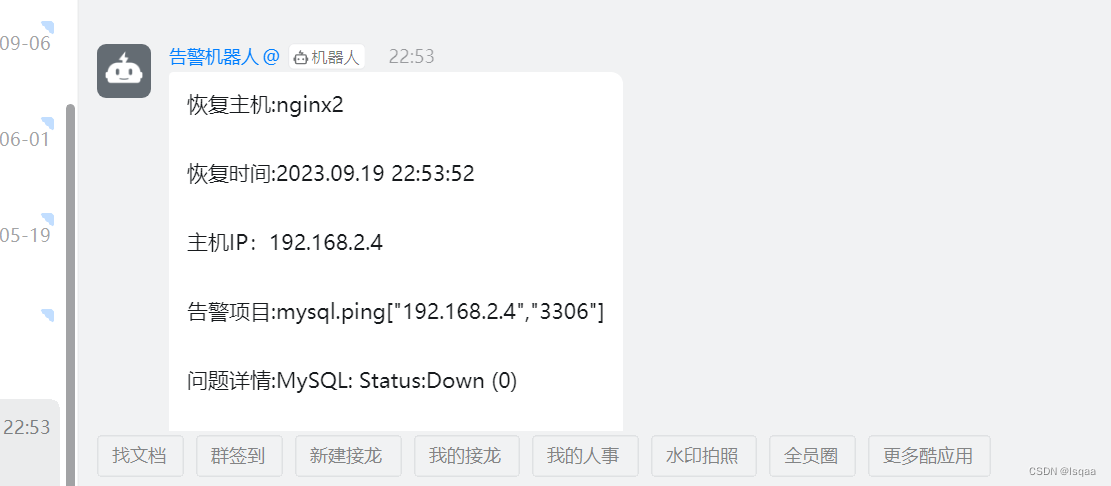
zabbix监控告警邮箱提醒,钉钉提醒
一、注册网易邮箱及其配置邮箱 1、开启POP3/SMTP/IMAP 二、service端配置邮件服务 1.安装 mailx dos2unix yum install -y mailx dos2unix mailx:邮件服务 mos2unix:用于转换文本文件格式的实用工具 查看mailx版本 2.配置mailx配置文件 编辑…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...
