AVL 树
文章目录
- 一、AVL 树的概念
- 二、AVL 树的实现
- 1. AVL 树的存储结构
- 2. AVL 树的插入
一、AVL 树的概念
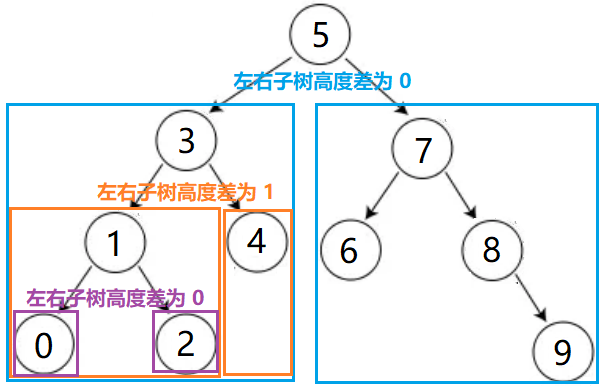
在 二叉搜索树 中,当我们连续插入有序的数据时,二叉搜索树可能会呈现单枝树的情况,此时二叉搜索树的查找效率为 O(N)
俄罗斯的两位数学家 G. M. Adelson-Velsky 和 E. M. Landis 发明了 AVL 树可以解决上述问题,AVL 树保证树中的每个结点的左右子树高度差不会超过 1,从而保证 AVL 树是一颗高度平衡的二叉搜索树,从而保证 AVL 树的搜索效率为 O(log N),AVL 树的名字就是取自于这两位科学家
一颗 AVL 树是 空树 或者满足如下条件:
- 左右子树的高度差小于等于 1 的二叉搜索树
- 左右子树均为 AVL 树
AVL 树是一颗在二叉搜索树并且满足所有结点的左右子树高度差不超过 1
二、AVL 树的实现
AVL 树有很多实现方式,这里采用三叉链和平衡因子,结点的平衡因子的值为右子树的高度减去左子树的高度,通过控制所有结点的平衡因子的绝对值小于等于 1,并且保证该树为二叉搜索树,即可实现 AVL 树
1. AVL 树的存储结构
// AVL 树的结点
template<class K, class V>
struct AVLTreeNode
{std::pair<K, V> _kv;AVLTreeNode<K, V>* _parent;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;int _bf; // 平衡因子: 右子树的高度前去左子树的高度AVLTreeNode<K, V>(const std::pair<K, V>& kv = std::pair<K, V>(K(), V())): _kv(kv), _parent(nullptr), _left(nullptr), _right(nullptr), _bf(0){}
};// AVL 树
template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:AVLTree<K, V>(): _root(nullptr){}private:Node* _root;
};
2. AVL 树的插入
首先按照二叉搜索树的方式插入结点,保证插入结点之后还是二叉搜索树,当插入结点完成之后,该结点的祖先结点的平衡因子可能会受到影响,如果插入结点在祖先结点的左子树中,则祖先结点的 _bf --,否则该结点的 _bf ++(平衡因子的值为右子树的高度减去左子树的高度)
祖先结点的 _bf 更新后,有三种情况 _bf == 0 和 _bf == -1 || _bf == 1 以及 _bf == -2 || _bf == 2
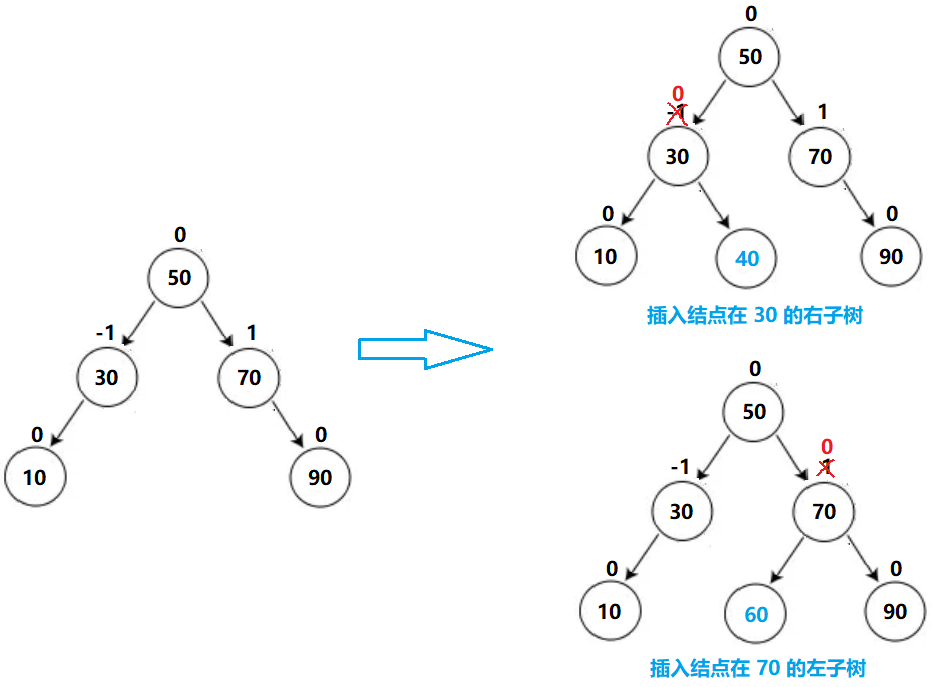
- 当 _bf == 0 时:当前更新 _bf 的结点所在的子树高度没有变化,此时不用继续更新祖先结点的 _bf
如果插入结点在祖先结点的右子树,祖先结点的平衡因子从 -1 -> 0
如果插入结点在祖先节点的左子树,祖先结点的平衡因子从 1 -> 0
无论是这两种的那种情况,对于更新后 _bf == 0 的结点的祖先结点而言,子树的高度是没有变化的
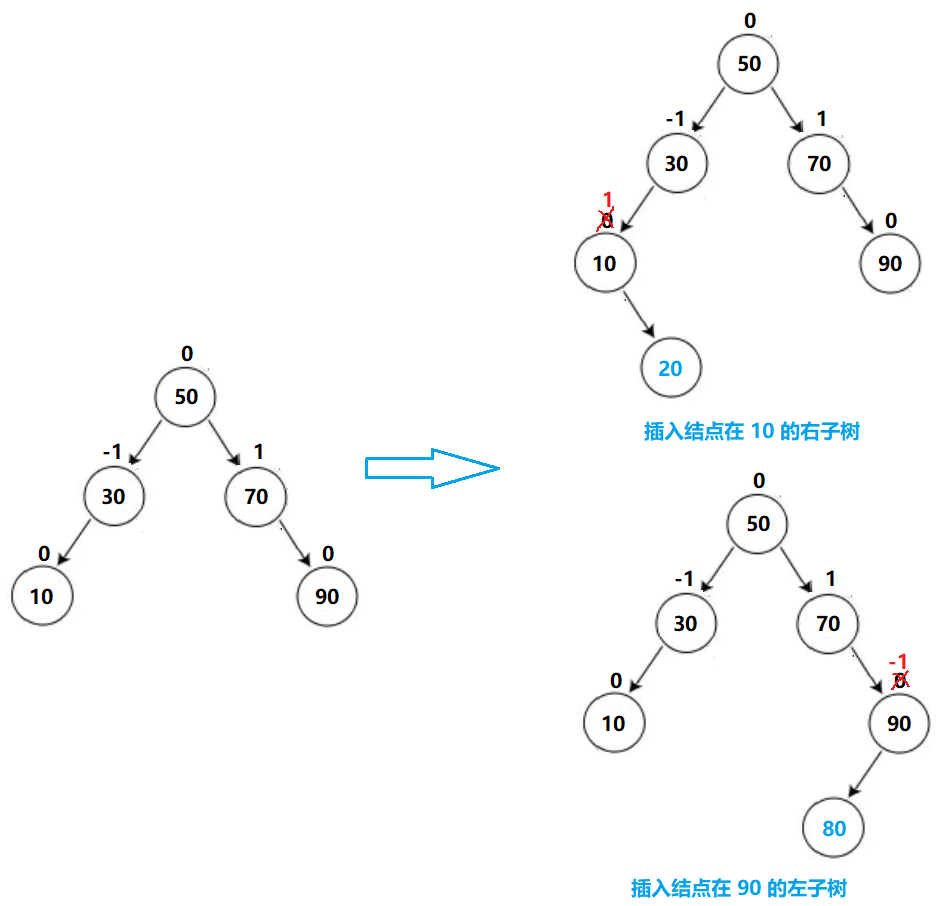
- 当 _bf == -1 || _bf == 1 时,当前更新 _bf 的结点所在的子树高度增加了,此时需要继续更新祖先结点的 _bf
如果插入结点在祖先结点的右子树,祖先结点的平衡因子从 0 -> 1
如果插入结点在祖先节点的左子树,祖先结点的平衡因子从 0 -> -1
无论是这两种的那种情况,对于更新后 _bf == -1 || _bf == 1 的结点的祖先结点而言,子树的高度都增加了 1
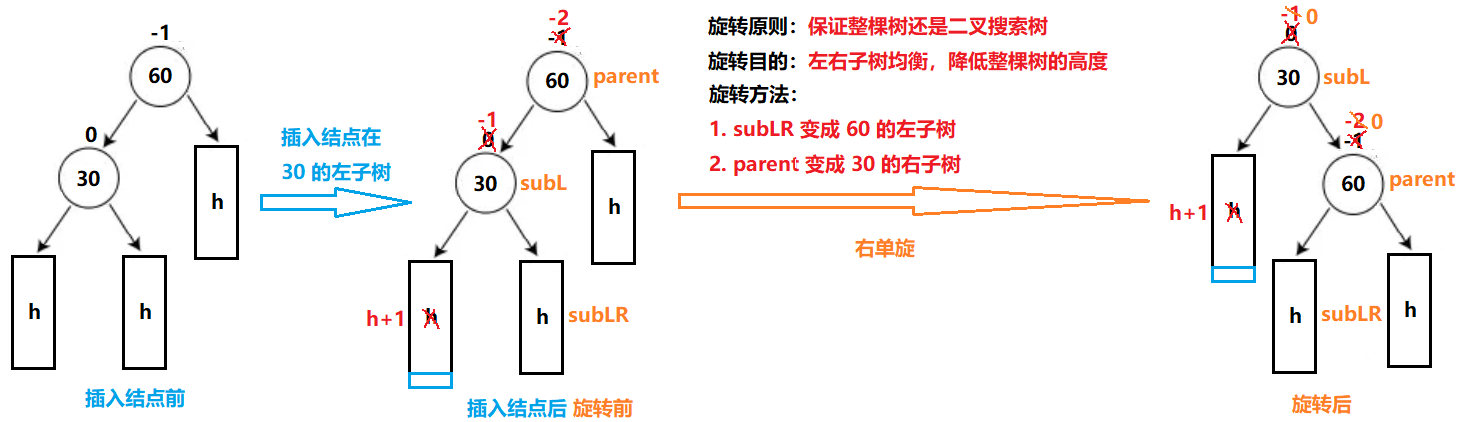
- 当 _bf == -2 || _bf == 2 时,当前更新 _bf 的结点左右子树高度差超过 1 了,已经不平衡了,此时需要对该结点所在的子树进行旋转,旋转之后该结点的 _bf 会变成 0,此时也不用继续更新祖先结点的 _bf 了
旋转有四种情况:右单旋、左单旋、左单旋再右单旋、右单旋再左单旋
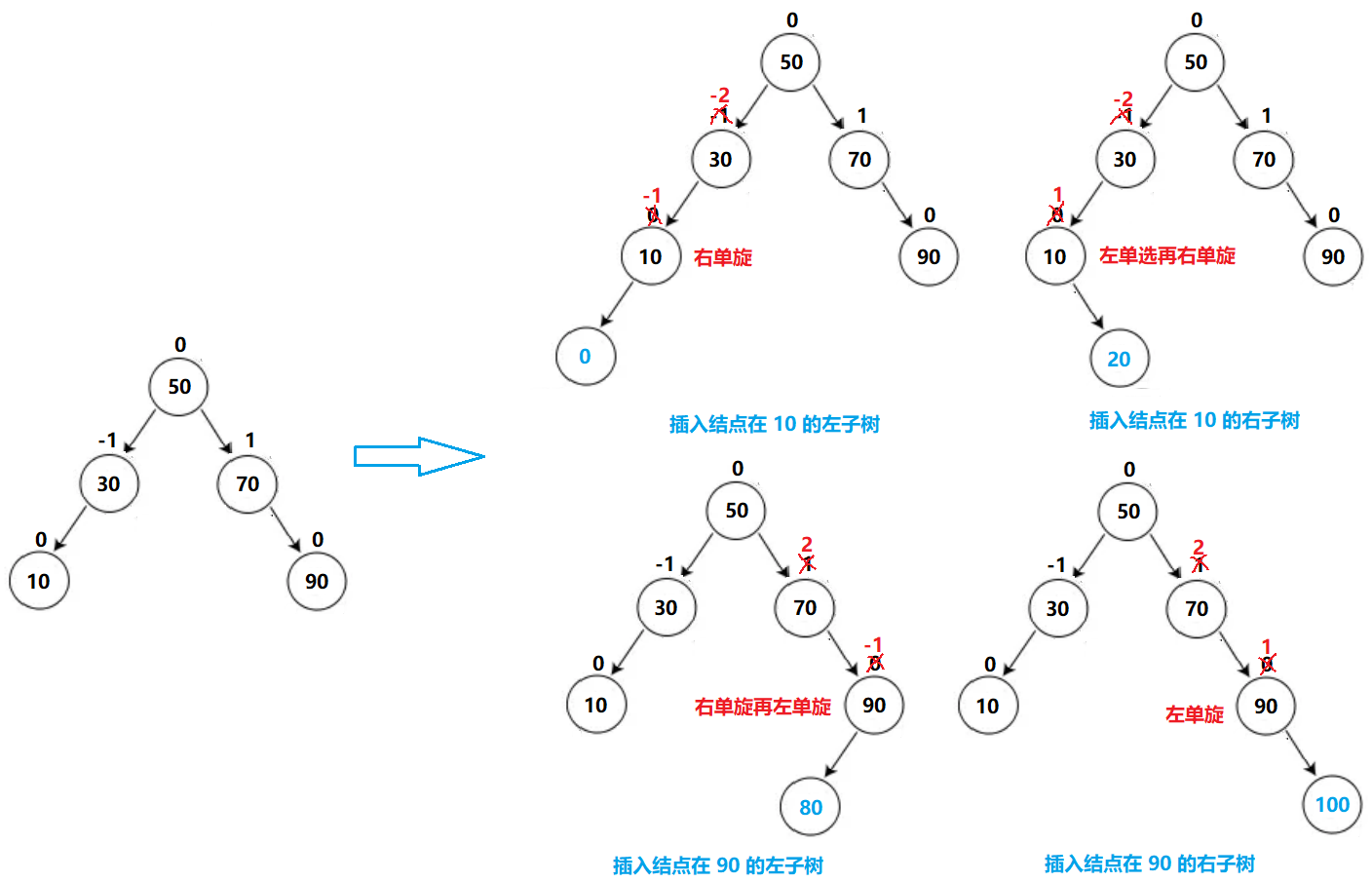
- 右单旋:插入结点在较高左子树的左侧
-
左单旋:插入结点在较高右子树的右侧,旋转方法类似于右单旋
-
左单旋再右单旋:插入结点在较高左子树的右侧,旋转方法类似于右单旋再左单旋
-
右单旋再左单旋:插入结点在较高右子树的左侧
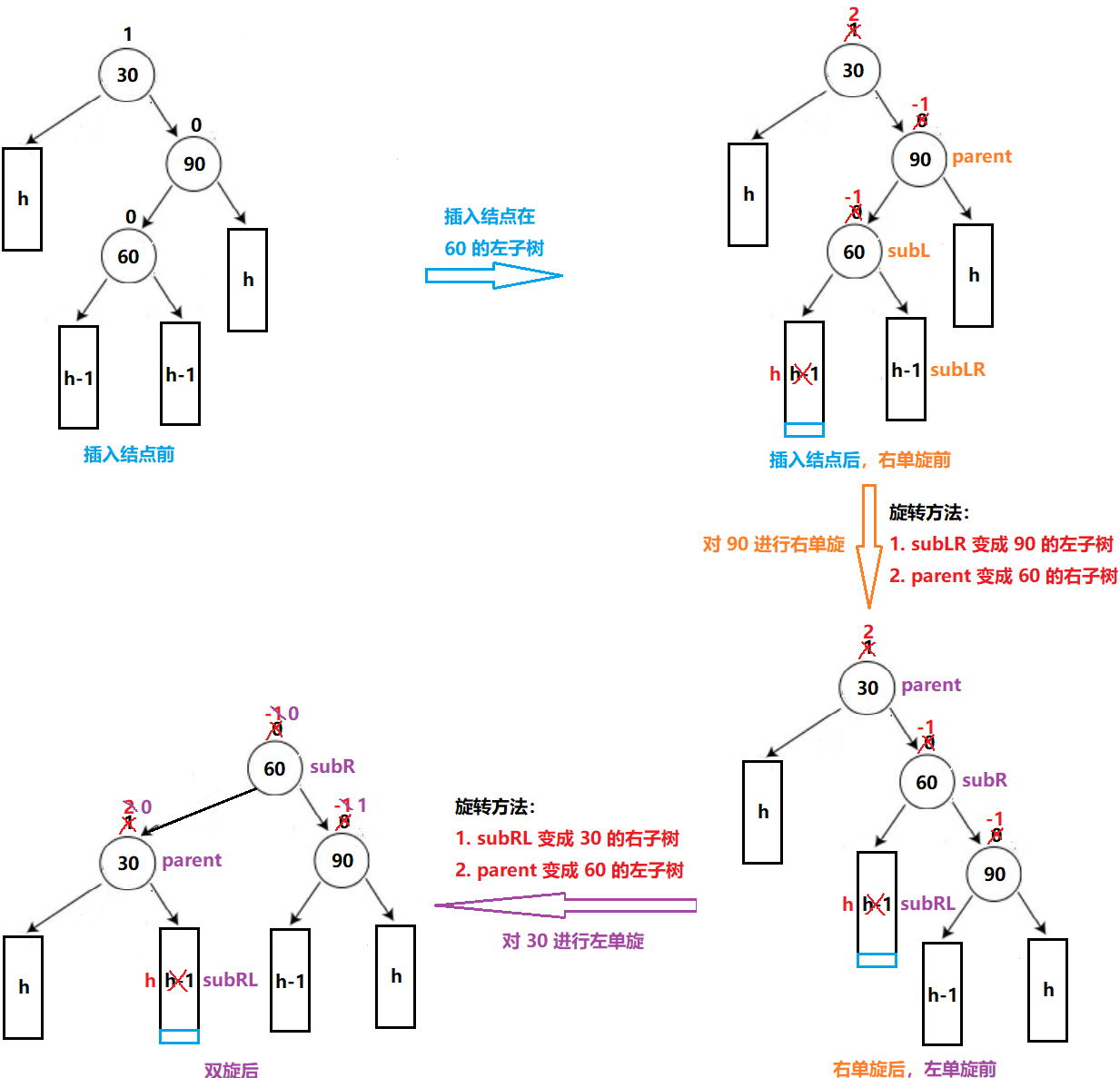
// 右单旋
void RotateR(Node* parent)
{Node* pparent = parent->_parent;Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR) subLR->_parent = parent;subL->_right = parent;parent->_parent = subL;if (pparent == nullptr) _root = subL;else{if (pparent->_kv.first > subL->_kv.first) pparent->_left = subL;else pparent->_right = subR;}subL->_parent = pparent;
}// 左单旋
void RotateL(Node* parent)
{Node* pparent = parent->_parent;Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL) subRL->_parent = parent;subR->_left = parent;parent->_parent = subR;if (pparent == nullptr) _root = subR;else{if (pparent->_kv.first > subR->_kv.first) pparent->_left = subR;else pparent->_right = subR;}subR->_parent = pparent;
}// 插入
bool Insert(const std::pair<K, V>& kv)
{// 按照二叉搜索树的方式插入结点,保证该树插入结点之后还是二叉搜索树if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else return false;}cur = new Node(kv);if (parent->_kv > kv.first) parent->_left = cur;else parent->_right = cur;cur->_parent = parent;// 更新平衡因子while (parent){// 如果插入结点在祖先结点的左子树,_bf--// 如果插入结点在祖先结点的右子树,_bf++if (parent->_left == cur) parent->_bf--;else parent->_bf++;// 当 _bf == 0 时,结点所在的子树高度没有变化,不用继续更新祖先结点的 _bf// 当 _bf == -1 || _bf == 1 时,结点所在的子树高度增加 1,需要继续更新祖先结点的 _bf,最多更新到根结点// 当 _bf == -2 || _bf == 2 时,结点所在的子树不平衡了,需要对子树进行旋转,旋转之后 _bf 变为 0,也不用继续更新祖先结点的 _bf 了// 当 _bf 为其他值时,说明出大问题了if (parent->_bf == 0) break;else if (parent->_bf == -1 || parent->_bf == 1){// 继续更新parent = parent->_parent;cur = cur->_parent;}else if (parent->_bf == -2 || parent->_bf == 2){// 旋转// parent->_bf == -2 && cur->_bf == -1 右单旋// parent->_bf == 2 && cur->_bf == 1 左单旋// parent->_bf == -2 && cur->_bf == 1 左单旋再右单旋// parent->_bf == 2 && cur->_bf == -1 右单旋再左单旋// 当 _bf 为其他值时,说明出大问题了if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);parent->_bf = 0;cur->_bf = 0;}else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent); parent->_bf = 0;cur->_bf = 0;}else if (parent->_bf == -2 && cur->_bf == 1){Node* sub = cur->_right;int bf = sub->_bf;RotateL(cur);RotateR(parent);// bf == 0 sub 就是新增// bf == -1 sub 左边新增// bf == 1 sub 右边新增sub->_bf = 0;if (bf == 0){parent->_bf = 0;cur->_bf = 0;}else if (bf == -1){parent->_bf = 1;cur->_bf = 0;}else if (_bf == 1){parent->_bf = 0;cur->_bf = -1;}else assert(false);}else if (parent->_bf == 2 && cur->_bf == -1){Node* sub = cur->_left;int bf = sub->_bf;RotateR(cur);RotateL(parent);// bf == 0 sub 就是新增// bf == -1 sub 左边新增// bf == 1 sub 右边新增sub->_bf = 0;if (bf == 0){parent->_bf = 0;cur->_bf = 0;}else if (bf == -1){parent->_bf = 0;cur->_bf = 1;}else if (bf == 1){parent->_bf = -1;cur->_bf = 0;}else assert(false);}else assert(false);break;}else assert(false);}return true;
}
相关文章:

AVL 树
文章目录 一、AVL 树的概念二、AVL 树的实现1. AVL 树的存储结构2. AVL 树的插入 一、AVL 树的概念 在 二叉搜索树 中,当我们连续插入有序的数据时,二叉搜索树可能会呈现单枝树的情况,此时二叉搜索树的查找效率为 O(N) 俄罗斯的两位数学家 …...
ggplot2做图(填坑中)
数据 df <- data.frame(x 1:10, y 1:10, f c(rep("A", 5), rep("B", 5))) 做图 1. 散点图 (scatter plot) # scatter plot scatter_plot <- function(df, metadata) {identical(rownames(df), rownames(metadata))data <- cbind(df, metada…...
Python日志处理器,同时打印到控制台和保存到文件中,并保证格式一致
使用logging模块的时候,默认是输出到控制台的,当然也可以配置输出到文件中,但是当你配置了文件后,控制台的输出就消失了,所以,需要一个策略即能保存到文件中,又能输出到控制台中。 下面是我做的…...
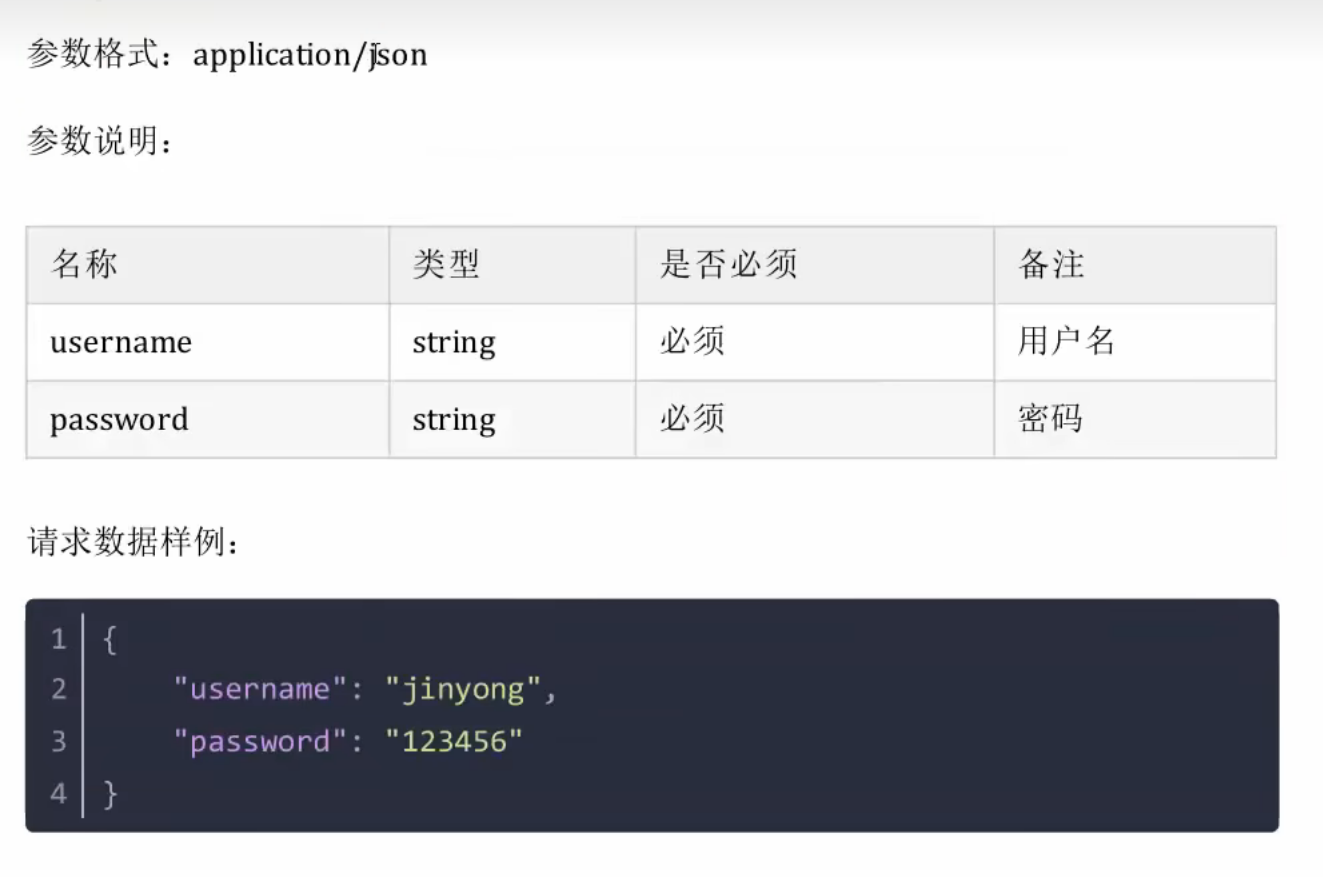
JavaWeb后端开发登录操作 登录功能 通用模板/SpringBoot整合
登录功能的思路 前端会传入两个参数:用户名和密码 在用户表中查询用户名,并校对相应的密码(涉及查询操作) SQL语句 select * from emp where username jingyong and password 123456; 如果有则成功,没有则登录失败.不可能为多个,因为添加了unique唯一约束,最终只会有一条 …...

The 2023 ICPC Asia Regionals Online Contest (1)(A D I J K L)
The 2023 ICPC Asia Regionals Online Contest (1)(A D I J K L) PTA | 程序设计类实验辅助教学平台 A Qualifiers Ranking Rules(模拟) 考虑先对第一场和第二场分别去重(取最好) , 归并排序后再次去重即可。 #include<bits/stdc.h> using namespace std;…...

C++ PrimerPlus 复习 第七章 函数——C++的编程模块(上)
第一章 命令编译链接文件 make文件 第二章 进入c 第三章 处理数据 第四章 复合类型 (上) 第四章 复合类型 (下) 第五章 循环和关系表达式 第六章 分支语句和逻辑运算符 第七章 函数——C的编程模块(上ÿ…...
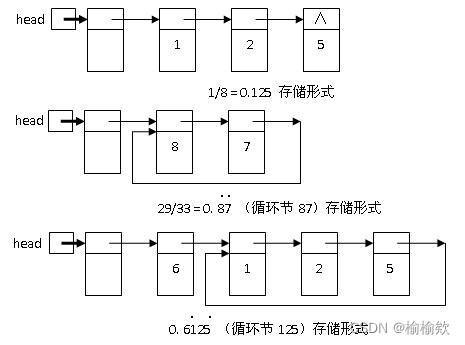
2.求循环小数
题目 对于任意的真分数 N/M ( 0 < N < M ),均可以求出对应的小数。如果采用链表表示各个小数,对于循环节采用循环链表表示,则所有分数均可以表示为如下链表形式。 输入: N M 输出: 转换…...
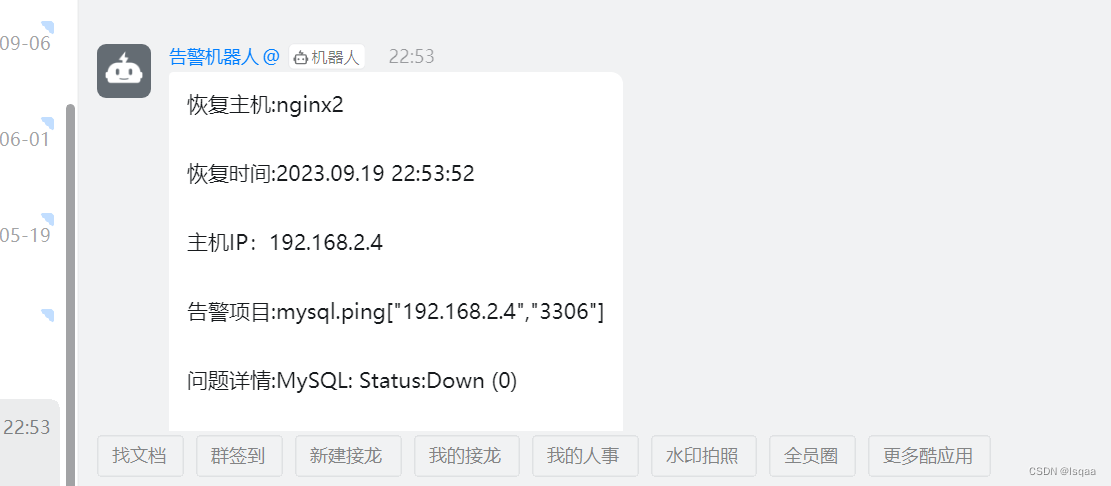
zabbix监控告警邮箱提醒,钉钉提醒
一、注册网易邮箱及其配置邮箱 1、开启POP3/SMTP/IMAP 二、service端配置邮件服务 1.安装 mailx dos2unix yum install -y mailx dos2unix mailx:邮件服务 mos2unix:用于转换文本文件格式的实用工具 查看mailx版本 2.配置mailx配置文件 编辑…...
典型数据结构-栈/队列/链表、哈希查找、二叉树(BT)、线索二叉树、二叉排序树(BST树)、平衡二叉树(AVL树)、红黑树(RB树)
目录 典型数据结构列举 栈/队列/链表 树 二叉树 线索二叉树 二叉排序树 平衡二叉树(AVL树) 红黑树 其它树种和应用介绍 典型数据结构列举 栈/队列/链表 描述略。 一些基本的简单实现参考/数据结构简单实现/文件夹里面。 线性表详解ÿ…...

pyarmor 加密许可证的使用
一 pyarmor 许可证的用处 文档:5. 许可模式和许可证 — Pyarmor 8.3.6 文档 试用版本有如下的限制: 加密功能对脚本大小有限制,不能加密超过限制的大脚本。 混淆字符串功能在试用版中无法使用。 RFT 加密模式,BCC 加密模式在试…...

网络路径监控分析
不间断的连接应该是任何企业的首要任务。然而,确保网络中的源和目标之间持续、不间断的联系一直是网络通信中一个劳动密集型的过程。了解网络路径中的障碍、识别它们并迅速解决它们以维护健康、不间断的网络至关重要。 为什么要监控网络路径 维护网络运行状况是任…...

vue双向数据绑定是如何实现的?
Vue中的双向数据绑定主要是通过数据劫持和发布订阅模式来实现的。 数据劫持: Vue通过使用Object.defineProperty()方法来对data对象中的属性进行劫持,从而实现对数据的双向绑定。具体实现方式为: (1)在Vue实例化时&a…...

el-date-picker 封装一个简单的日期组件, 主要是禁用日期
子组件 <template><div><el-date-pickerv-model"dateModel"type"datetimerange":picker-options"pickerOptions"range-separator"至"ref"picker"start-placeholder"开始日期"end-placeholder&quo…...
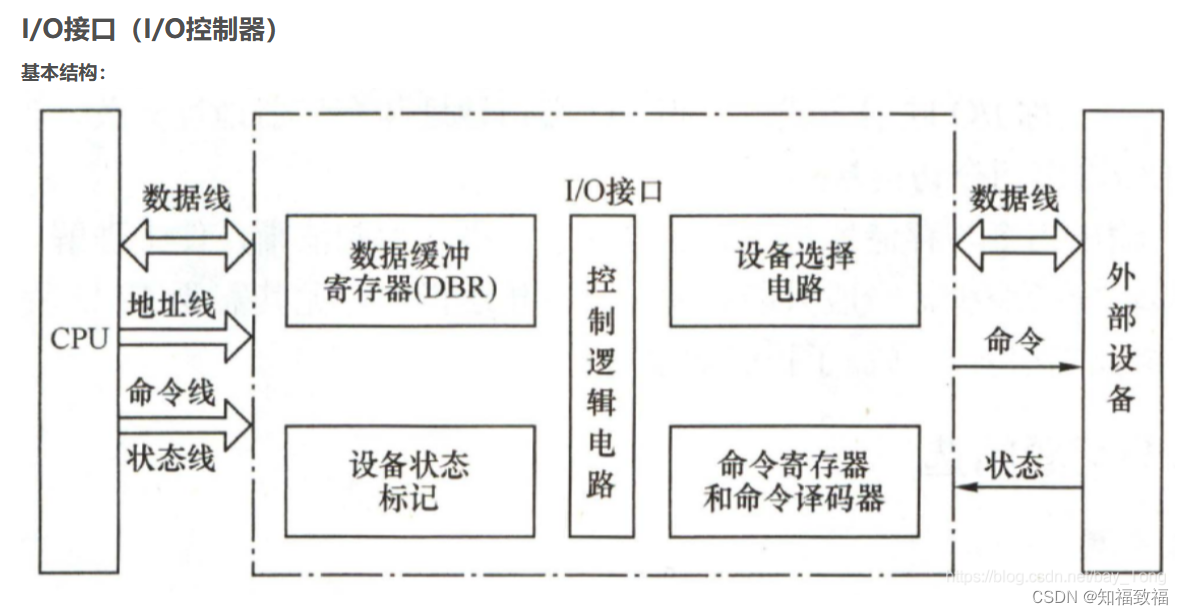
保研复习-计算机组成原理
计算机组成原理 计算机组成冯诺依曼体系结构计算机系统的层次结构计算机的五大组成部件编译和解释的区别 CPUCPU的组成寄存器的类型指令类型指令功能指令执行过程 存储器存储器的层次结构寻址方式 输入和输出io方式有哪几种IO接口的基本结构 计算机组成 冯诺依曼体系结构 存储…...
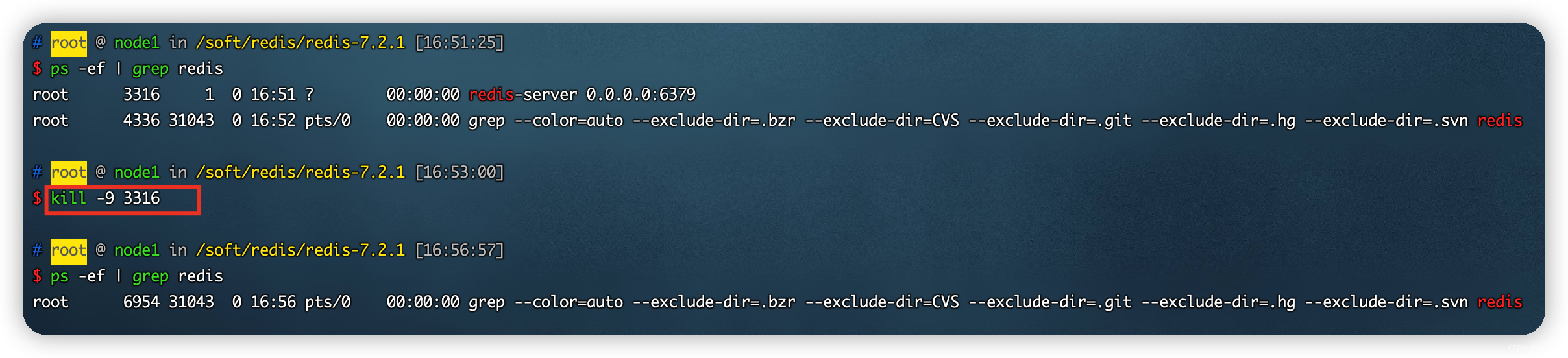
linux环境安装redis(亲测完成)
linux环境安装redis 亲测完成 前言一、redis简介Redis 与其他 key - value 缓存产品有以下三个特点:Redis 优势 二、安装redis1.下载安装包2.创建服务器安装路径3.上传安装包4.解压安装包5.依赖安装6.编译 三、启动1)默认启动错误解决方式 2)指定配置启动2.1&#x…...

关于命令行交互自动化,及pyinstaller打包wexpect的问题
Python自动化工具 用来执行命令并进行交互,比如需要输入账号密码或者确认的场景 linux平台可以用pexpect,但是windows平台有一些差异,比较好用的是pexpect的变种wexpect,如果脚本中用了wexpect,并且要打包成onefile&a…...

8.4 【MySQL】文件系统对数据库的影响
因为 MySQL 的数据都是存在文件系统中的,就不得不受到文件系统的一些制约,这在数据库和表的命名、表的大小和性能方面体现的比较明显,比如下边这些方面: 数据库名称和表名称不得超过文件系统所允许的最大长度。 每个数据库都对应…...
Python WEB框架FastAPI (二)
Python WEB框架FastAPI (二) 最近一直在使用fastapi,随着使用的深入发现我对于它的了解还是太少了,以至于踩了一些坑。所以在这里记录一下,愿看到的小伙伴不迷路。 路径传参并发问题 一、路径传参 这是对上一个传参…...

基于Java网络书店商城设计实现(源码+lw+部署文档+讲解等)
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...
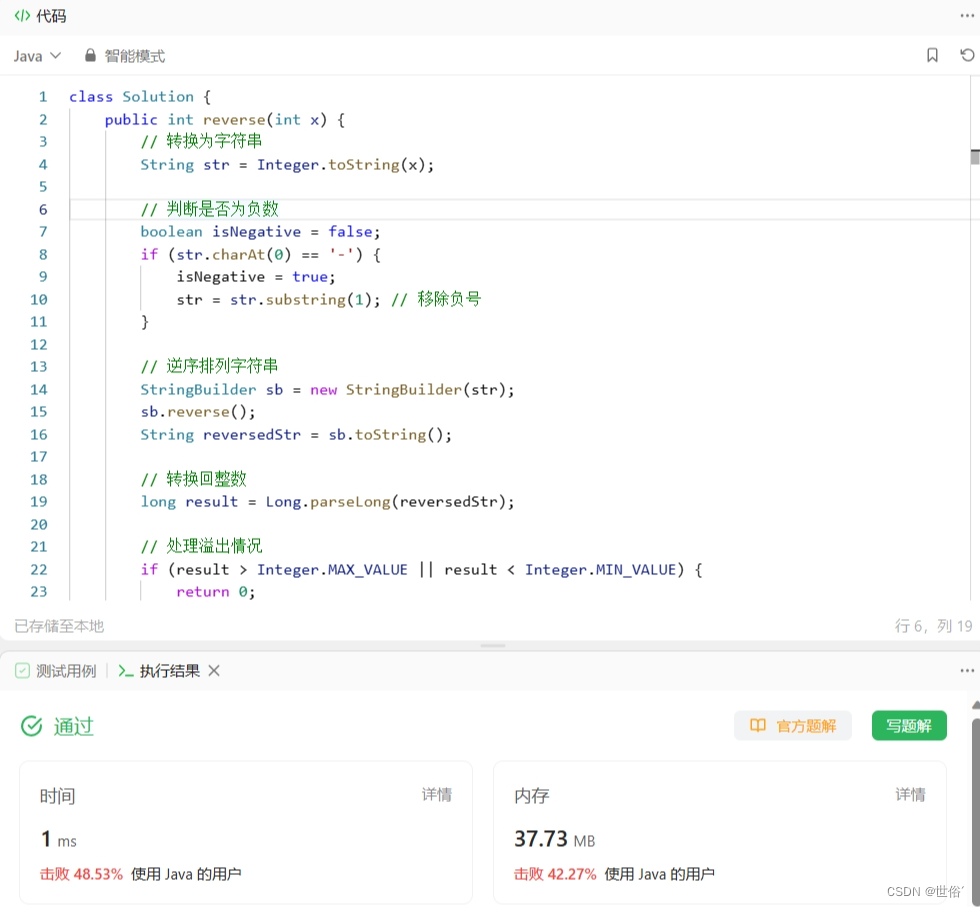
怒刷LeetCode的第3天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:动态规划 第二题 题目来源 题目内容 解决方法 方法一:模拟 方法二:数学规律 方法三:分组 第三题 题目来源 题目内容 解决方法 方法一:数学方法 方法…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...
