经典算法-----约瑟夫问题(C语言)
目录
前言
故事背景
约瑟夫问题
环形链表解决
数组解决
前言
今天我们来玩一个有意思的题目,也就是约瑟夫问题,这个问题出自于欧洲中世纪的一个故事,下面我们就去通过编程的方式来解决这个有趣的问题,一起来看看吧!

故事背景
据说著名犹太历史学家Josephus有过以下的故事:在罗马人占领乔塔帕特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始,越过k-2个人(因为第一个人已经被越过),并杀掉第k个人。接着,再越过k-1个人,并杀掉第k个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。问题是,给定了和,一开始要站在什么地方才能避免被处决。Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。
17世纪的法国数学家加斯帕在《数目的游戏问题》中讲了这样一个故事:15个教徒和15 个非教徒在深海上遇险,必须将一半的人投入海中,其余的人才能幸免于难,于是想了一个办法:30个人围成一圆圈,从第一个人开始依次报数,每数到第九个人就将他扔入大海,如此循环进行直到仅余15个人为止。问怎样排法,才能使每次投入大海的都是非教徒。

约瑟夫问题
从键盘获取两个数据,n和s,n是表示人数,s是表示从第一个人开始数,数到第s个的时候那个人就出局,问:最后剩下的最后一个人是第几个?
环形链表解决
这里我们可以去通过环形链表的形式来解决这个问题 ,过程图如下所示:

先根据当前输入的人数去创建一个相对应的环形链表,依次把每个人的位置存入进去

然后就去从第一个人开始数,当数到第三个人的时候就进行删除操作,如下所示,后面就从第四个节点开始新的一轮……

代码如下所示:
#include <stdio.h>
#include<stdlib.h>
//节点
typedef struct node {int num;struct node* next;
}Node;//创建一个环形链表
Node* create_list(int n) {Node* head, * tail;head = tail = NULL;for (int i = 0; i < n; i++) {Node* p = (Node*)malloc(sizeof(Node));p->num = i + 1; //依次标记当前位置if (head == NULL) {head = p;tail = p;head->next = NULL;}else{tail->next = p;tail = p;}tail->next = head;}return head; //返回头结点
}int main() {int n, s;printf("请输入:");scanf("%d %d", &n, &s);Node* cur = create_list(n);int count = 1; //此时cur指向的是第一个节点,所以count为1while (n != 1) { //当n=1时候,结束循环,此时剩下最后一个人count++;//先进行count统计if (count == s) {n--; //进行删除节点操作Node* del_node = cur->next; cur->next = del_node->next;free(del_node);//释放掉这个节点//此时count回归到1,也就是重新开始新的一轮count = 1;}cur = cur->next;}printf("最后剩下的是:%d\n", cur->num);
}数组解决
不同与链表的是,数组不能去自定义人的数量,也就是说这里数组的数量是提前写好了的,还有就是数组的执行效率更加高,环形链表要去通过遍历执行,时间复杂度为O(n),而数组可以去直接找到这个位置时间复杂度为O(1),不需要去一个一个遍历,代码如下:
//数组实现
#include<stdio.h>
void function(int* num, int length, int s, int start) {int count = 0;int i = start - 1;//标记起始位置int n = length; //当前人数while (n != 1) {i = (i + s - 1) % n; //下一个出局人的位置for (int j = i + 1; j < length; j++)num[j - 1] = num[j]; //进行删除操作,把要删除的数字后面的依次往前移动,覆盖掉这个要删除的数字n--;//删除操作完成,减少一个人if (i == n) { //当i超出数组范围的时候,i就回归到第一个为止i = 0;}}printf("最后一个 :%d", num[i]);return;
}int main() {int num[6];//这里就已经定义好了6个人int s; //每次数到s,出局一个printf("请输入:");scanf("%d", &s);for (int i = 0; i < sizeof(num) / sizeof(int); i++)num[i] = i+1;function(num, sizeof(num) / sizeof(int), s, 0);
}以上就是今天的内容,我们下次见!
分享一张壁纸:
相关文章:

经典算法-----约瑟夫问题(C语言)
目录 前言 故事背景 约瑟夫问题 环形链表解决 数组解决 前言 今天我们来玩一个有意思的题目,也就是约瑟夫问题,这个问题出自于欧洲中世纪的一个故事,下面我们就去通过编程的方式来解决这个有趣的问题,一起来看看吧!…...

代码随想录 动态规划Ⅴ
494. 目标和 给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 或 - ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ,在 1 之前添加 - …...
驱动DAY9
驱动文件 #include <linux/init.h> #include <linux/module.h> #include <linux/of.h> #include <linux/of_gpio.h> #include <linux/gpio.h> #include <linux/fs.h> #include <linux/io.h> #include <linux/device.h> #incl…...

03贪心:摆动序列
03贪心:摆动序列 376. 摆动序列 局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。 整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。…...

javascript获取元素在浏览器中工作区域的左、右、上、下距离,或带滚动条的元素在页面中的大小
//获取元素在包含元素框中的大小 //第1个函数为获取元素在包含元素中左内边框的距离 function getELementLeft(element){//获取元素在包含元素左边距离var actualeftelement.offsetLeft;//获取元素的上级包含元素var currentelement.offsetParent;//循环到一直没有包含元素whil…...
VSCode 安装使用教程 环境安装配置 保姆级教程
一个好用的 IDE 不仅能提升我们的开发效率,还能让我们保持愉悦的心情,这样才是非常 Nice 的状态 ^_^ 那么,什么是 IDE 呢 ? what IDE(Integrated Development Environment,集成开发环境)是含代码…...
c盘中temp可以删除吗?appdata\local\temp可以删除吗?
http://www.win10d.com/jiaocheng/22594.html C盘AppData文件夹是一个系统文件夹,里面存储着临时文件,各种应用的自定义设置,快速启动文件等。近期有用户发现appdata\local\temp占用了大量的空间,那么该文件可以删除吗?…...

Java手写聚类算法
Java手写聚类算法 1. 算法思维导图 以下是聚类算法的实现原理的思维导图,使用Mermanid代码表示: #mermaid-svg-AK9EgYRS38PkRJI4 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-AK9EgYRS38…...
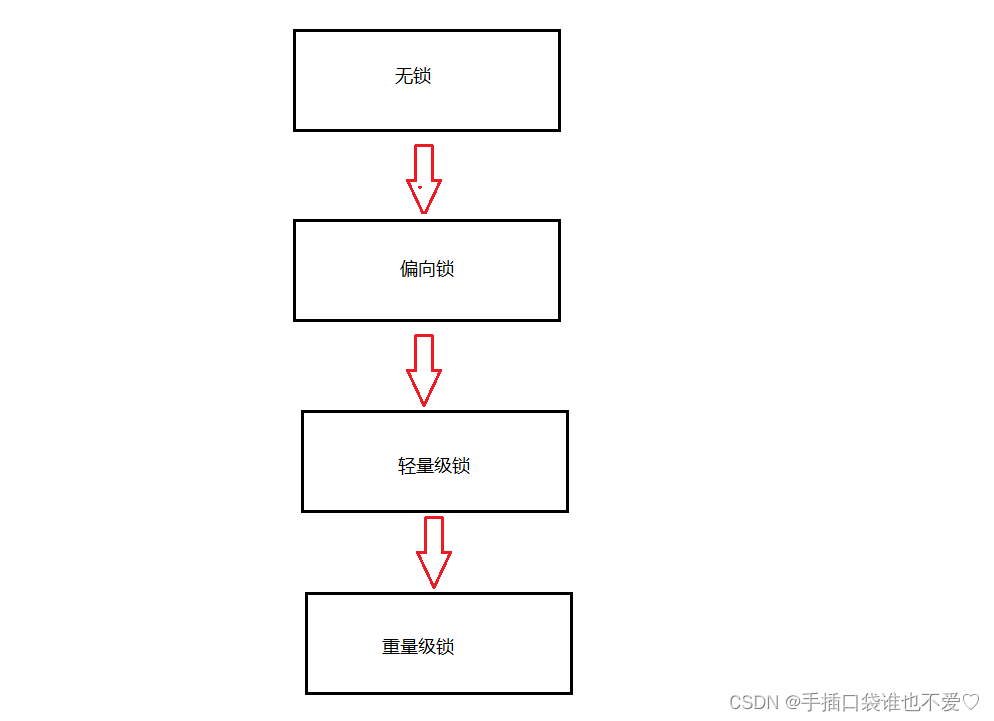
解密Java多线程中的锁机制:CAS与Synchronized的工作原理及优化策略
目录 CAS什么是CASCAS的应用ABA问题异常举例 Synchronized 原理基本特征加锁过程偏向锁轻量级锁重量级锁 其他优化操作锁消除锁粗化 CAS 什么是CAS CAS: 全称Compare and swap,字面意思:”比较并交换“,CAS涉及如下操作: 假设内存中的原数据…...

solid works草图绘制与设置零件特征的使用说明
(1)草图绘制 • 草图块 在 FeatureManager 设计树中,您可以隐藏和显示草图的单个块。您还可以查看块是欠定义 (-)、过定义 () 还是完全定义。 要隐藏和显示草图的单个块,请在 FeatureManager 设计树中右键单击草图块,…...
页面跳转后,该页面不刷新问题)
vue3使用router.push()页面跳转后,该页面不刷新问题
文章目录 原因分析最优解决 原因分析 这是一个常见问题,当使用push的时候,会向history栈添加一个新记录,这个时候,再添加一个完全相同的路由时,就不会再次刷新了 最优解决 在页面跳转时加上params参数时间 router.…...

如何理解数字工厂管理系统的本质
随着科技的飞速发展和数字化转型的推动,数字工厂管理系统逐渐成为工业4.0时代的重要工具。数字工厂系统旨在整合和优化工厂运营的各个环节,通过实时数据分析和处理,提升生产效率,降低成本,并增强企业的整体竞争力。为了…...
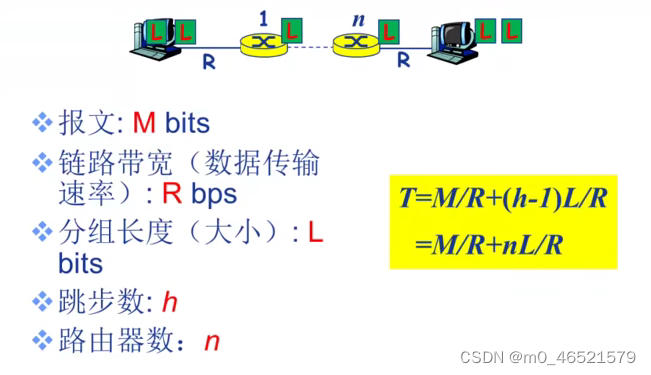
笔记1.3 数据交换
如何实现数据通过网络核心从源主机到达目的主机? 数据交换 交换网络: 动态转接动态分配传输资源 数据交换类型: (1)电路交换 (2)报文交换 (3)分组交换 电路交换的特…...
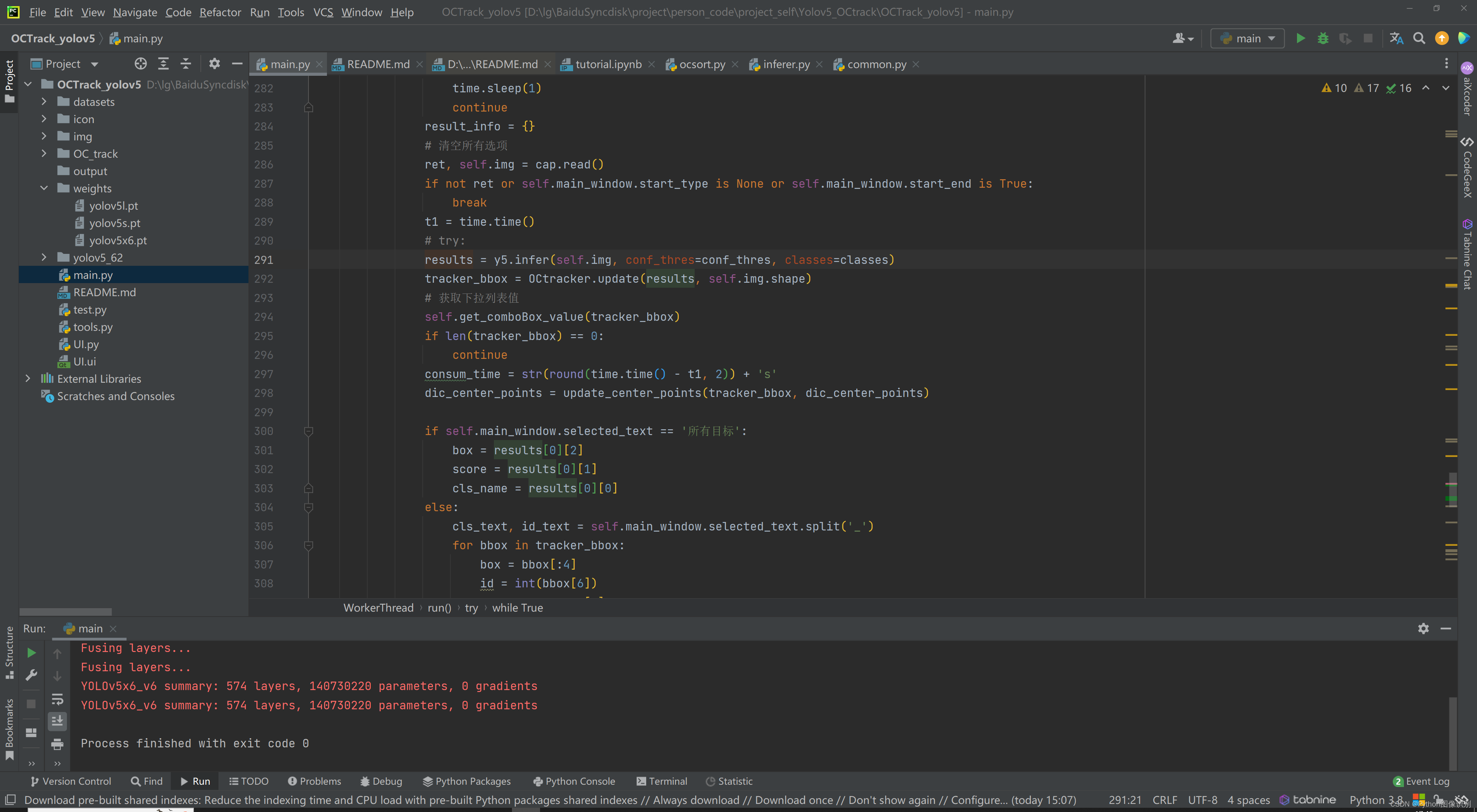
实时车辆行人多目标检测与跟踪系统(含UI界面,Python代码)
算法架构: 目标检测:yolov5 目标跟踪:OCSort其中, Yolov5 带有详细的训练步骤,可以根据训练文档,训练自己的数据集,及其方便。 另外后续 目标检测会添加 yolov7 、yolox,目标跟踪会…...

谷歌AI机器人Bard发布强大更新,支持插件功能并增强事实核查;全面整理高质量的人工智能、机器学习、大数据等技术资料
🦉 AI新闻 🚀 谷歌AI机器人Bard发布强大更新,支持插件功能并增强事实核查 摘要:谷歌的人工智能聊天机器人Bard发布了一项重大更新,增加了对谷歌应用的插件支持,包括 Gmail、Docs、Drive 等,并…...

NI SCXI-1125 数字量控制模块
NI SCXI-1125 是 NI(National Instruments)生产的数字量控制模块,通常用于工业自动化和控制系统中,以进行数字输入和输出控制。以下是该模块的一些主要产品特点: 数字量输入:SCXI-1125 模块通常具有多个数字…...
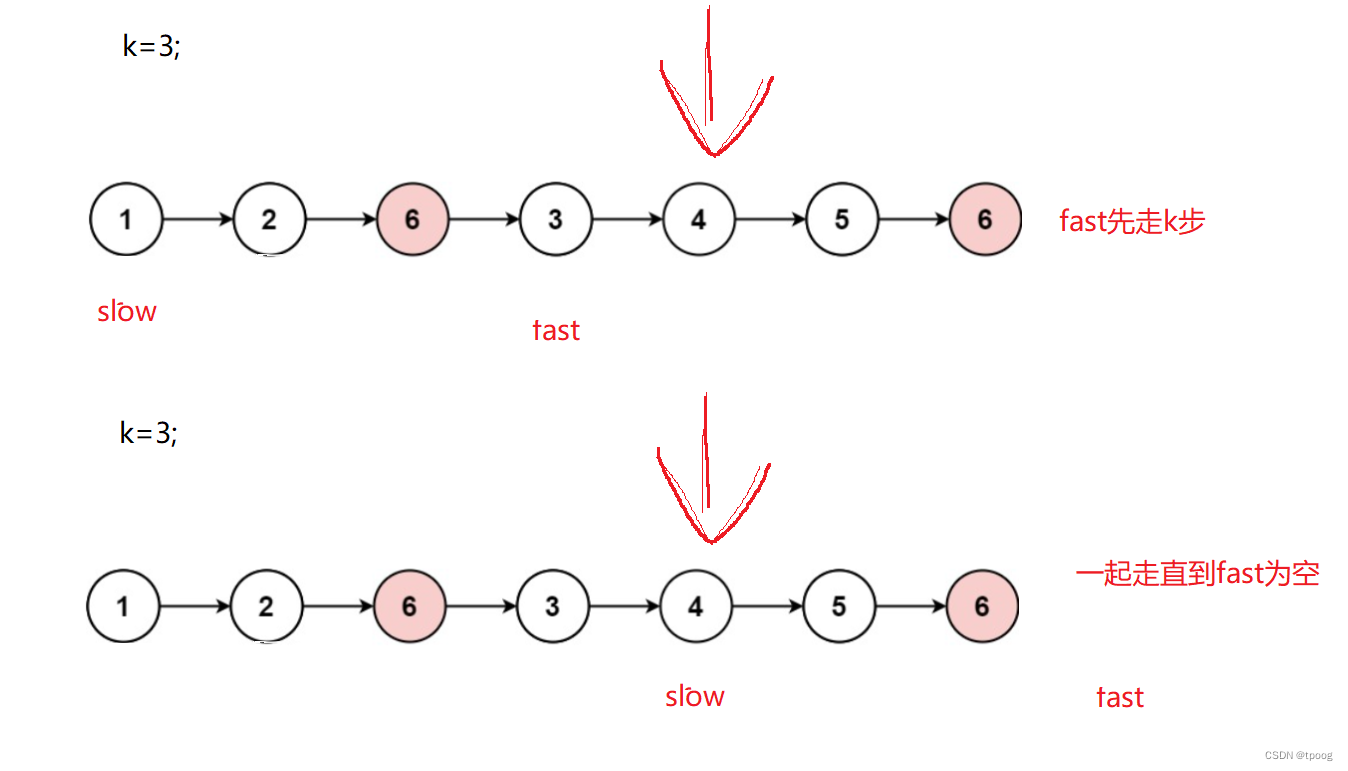
链表oj题1(Leetcode)——移除链表元素,反转链表,链表的中间节点,
链表OJ 一,移除链表元素1.1分析1.2代码 二,找到链表的中间节点2.1分析2.2代码 三,反转链表3.1分析3.2代码 四,找到链表中倒数第k个节点4.1分析4.2代码 一,移除链表元素 移除链表元素 1.1分析 这里的删除要分成两种…...
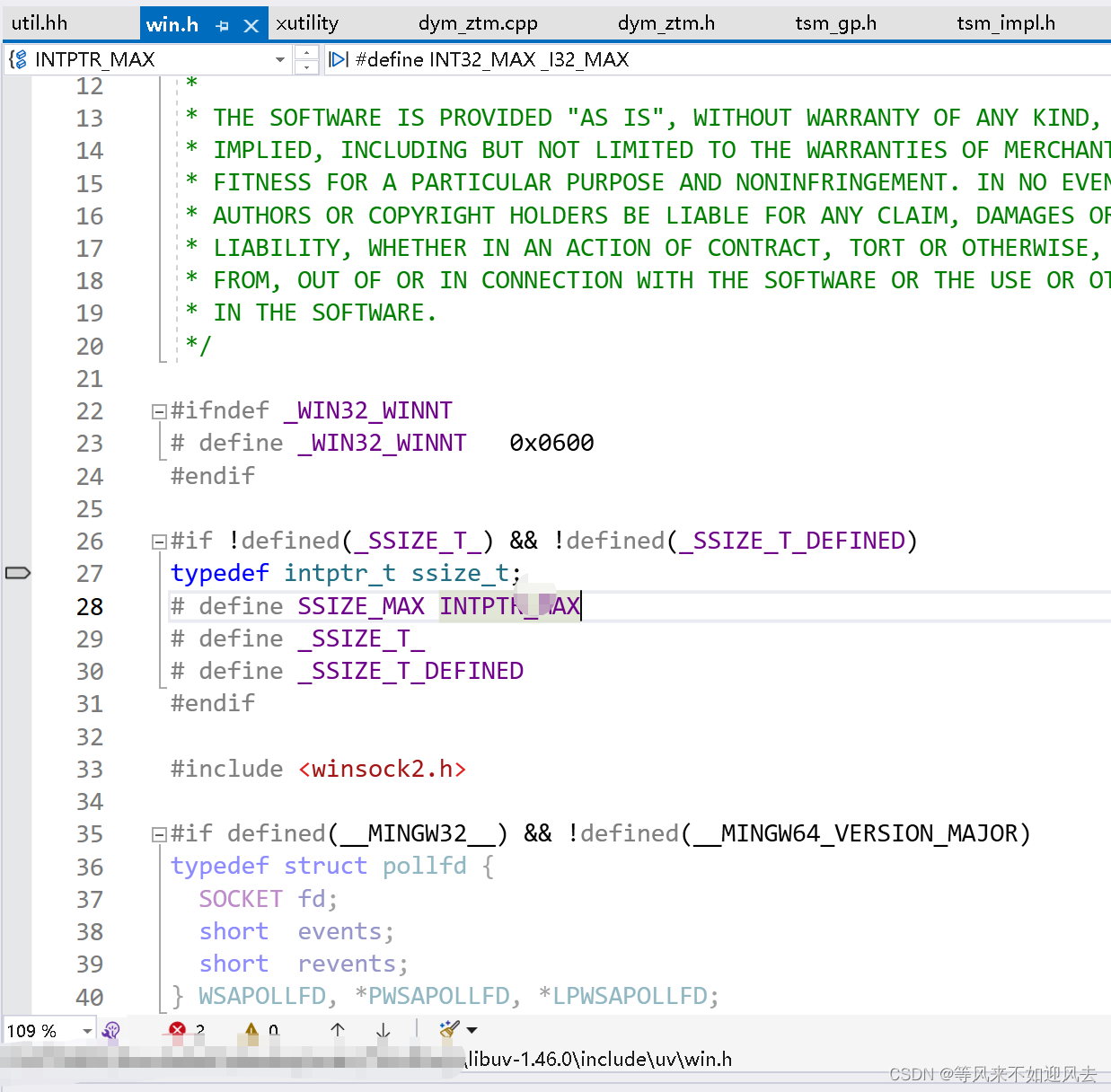
【libuv】与uvgrtrp的_SSIZE_T_定义不同
libuv的 #if !defined(_SSIZE_T_) && !defined(_SSIZE_T_DEFINED) typedef intptr_t ssize_t;...

安卓ROM定制 修改必备常识-----初步了解system系统分区文件夹的基本含义 【二】
安卓修改rom 固件 修改GSI 移植rom 必备常识 lib--**so文件基本解析 一起来了解system目录相应文件的用途吧。(rom版本不同里面的app也会不一样) 简单打开img格式后缀文件 给大家说下最简单的方法提取img里面的文件,对于后缀img格式的文件可…...

GPT会统治人类吗
一 前言 花了大概两天时间看完《这就是ChatGPT》,触动还是挺大的,让我静下来,认真地想一想,是否真正理解了ChatGPT,又能给我们以什么样的启发。 二 思考 在工作和生活中,使用ChatGPT或文心一言,…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
