【AI】机器学习——支持向量机(非线性及分析)
5. 支持向量机(线性SVM)
文章目录
- 5.4 非线性可分SVM
- 5.4.1 非线性可分问题
- 处理思路
- 核技巧
- 核函数
- 特点
- 核函数作用于SVM
- 5.4.2 正定核函数
- 5.5 SVM参数求解算法
- 5.6 SVM与线性模型关系
5.4 非线性可分SVM
5.4.1 非线性可分问题
原始空间不存在能够正确划分的超平面
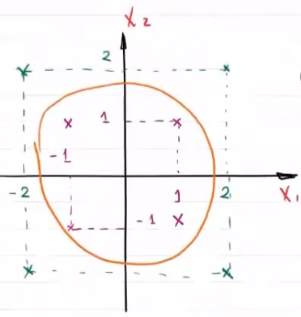
在二维平面直角坐标系中,如果按照与原点之间的距离对数据点进行分类的话,分类模型就成为一个圆,也就是超平面
处理思路
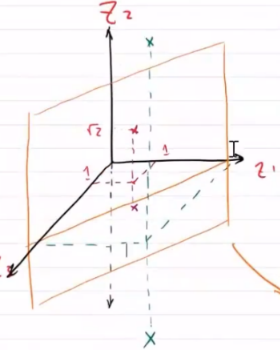
如果能将样本从原始空间映射到高维特征空间上,在新的特征空间是上样本就可能是线性可分的
- 若样本的属性数优先,则一定存在一个高维特征空间使样本可分
核技巧
通过一个非线性映射,将原始低维空间上的非线性问题转化为新的高维空间上的线性问题,这就是核技巧的基本思想。
使在原始空间 R n R^n Rn 中的超平面模型映射为特征空间的超平面模型
在学习和预测中,只定义核函数,而不显式定义映射函数,利用线性分类方法与核函数解决非线性问题
核函数
假设原始空间是 低维欧几里得空间 X \mathcal{X} X ,新空间为 **高维希尔伯特空间 H \mathcal{H} H ** ,从 X \mathcal{X} X 到 H \mathcal{H} H 的映射可以用函数 ϕ ( x ) : X → H \phi(x):\mathcal{X}\rightarrow \mathcal{H} ϕ(x):X→H 表示。核函数可以表示为映射函数内积形式
K ( x , z ) = ϕ ( x ) ⋅ ϕ ( z ) K(x,z)=\phi(x)\cdot\phi(z) K(x,z)=ϕ(x)⋅ϕ(z)
eg
原空间 X \mathcal{X} X 中的两个点进行内积运算 ( x i , x j ) (x_i,x_j) (xi,xj) ,若先进行映射再在 H \mathcal{H} H 中内积运算,则有
z i = ϕ ( x i ) , z j = ϕ ( x j ) , 则 ( z i , z j ) = ϕ ( x i ) ⋅ ϕ ( x j ) z_i=\phi(x_i),z_j=\phi(x_j),则(z_i,z_j)=\phi(x_i)\cdot \phi(x_j) zi=ϕ(xi),zj=ϕ(xj),则(zi,zj)=ϕ(xi)⋅ϕ(xj)
若使用核函数,则可直接计算 K ( x i , x j ) K(x_i,x_j) K(xi,xj)
特点
对于确定的核函数
-
计算过程在低维空间上完成,避免了高维空间中的复杂计算
-
对于给定核函数,高维空间 H \mathcal{H} H 和映射函数 ϕ \phi ϕ 的取法不唯一
可映射到不同的特征空间, z i z_i zi 维度可以不同和
可通过不同映射函数,映射到同一特征空间
核函数作用于SVM
输入:线性不可分的数据
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } ∈ X ∈ R n , y i ∈ Y ∈ { + 1 , − 1 } , i = 1 , ⋯ , N D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}\in \mathcal{X}\in R^n,y_i\in \mathcal{Y}\in \{+1,-1\},i=1,\cdots,N D={(x1,y1),(x2,y2),⋯,(xN,yN)}∈X∈Rn,yi∈Y∈{+1,−1},i=1,⋯,N
输出:分离超平面和决策函数
算法:
1. 选择合适的参数 C C C 和核函数 K ( x , z ) K(x,z) K(x,z) ,构造最优化问题
线性SVM
{ min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j x i ⋅ x j − ∑ i = 1 N α i s . t . 0 ≤ α i ≤ 0 ∑ i = 1 N α i y i = 0 \begin{cases} \min\limits_{\alpha}\frac{1}{2}\sum\limits_{i=1}^N\sum\limits_{j=1}^N\alpha_i\alpha_jy_iy_jx_i\cdot x_j-\sum\limits_{i=1}^N\alpha_i\\ s.t. \quad 0\le \alpha_i\le 0\\ \qquad \sum\limits_{i=1}^N\alpha_iy_i=0\\ \end{cases} ⎩ ⎨ ⎧αmin21i=1∑Nj=1∑Nαiαjyiyjxi⋅xj−i=1∑Nαis.t.0≤αi≤0i=1∑Nαiyi=0
对于 ( x i , x j ) (x_i,x_j) (xi,xj) ,可以通过核技巧映射到线性可分空间
ϕ ( x i ) ⋅ ϕ ( x j ) = z i ⋅ z j = K ( x i , x j ) \phi(x_i)\cdot \phi(x_j)=z_i\cdot z_j=K(x_i,x_j) ϕ(xi)⋅ϕ(xj)=zi⋅zj=K(xi,xj)
在 H \mathcal{H} H 空间中的SVM问题为
{ min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( x i , x j ) − ∑ i = 1 N α i s . t . 0 ≤ α i ≤ 0 ∑ i = 1 N α i y i = 0 \begin{cases} \min\limits_{\alpha}\frac{1}{2}\sum\limits_{i=1}^N\sum\limits_{j=1}^N\alpha_i\alpha_jy_iy_jK(x_i,x_j)-\sum\limits_{i=1}^N\alpha_i\\ s.t. \quad 0\le \alpha_i\le 0\\ \qquad \sum\limits_{i=1}^N\alpha_iy_i=0\\ \end{cases} ⎩ ⎨ ⎧αmin21i=1∑Nj=1∑NαiαjyiyjK(xi,xj)−i=1∑Nαis.t.0≤αi≤0i=1∑Nαiyi=0
求得最优解 α ∗ = ( α 1 ∗ , α 2 ∗ , ⋯ , α N ∗ ) \alpha^*=(\alpha_1^*,\alpha_2^*,\cdots,\alpha_N^*) α∗=(α1∗,α2∗,⋯,αN∗)
2. 选一个 0 < α j ∗ < C 0<\alpha_j^*<C 0<αj∗<C 的分量对应的样本点 ( x j , y j ) (x_j,y_j) (xj,yj) ——支持向量,计算模型参数 ω ∗ , b ∗ \omega^*,b^* ω∗,b∗
有 ω ∗ = ∑ i = 1 N α i ∗ y i K ( ⋅ , x i ) \omega^*=\sum\limits_{i=1}^N\alpha_i^*y_i K(\cdot,x_i) ω∗=i=1∑Nαi∗yiK(⋅,xi) , b ∗ = y j − ∑ i = 1 N α i ∗ y i K ( x i , x j ) b^*=y_j-\sum\limits_{i=1}^N\alpha_i^*y_iK(x_i,x_j) b∗=yj−i=1∑Nαi∗yiK(xi,xj)
模型
{ ∑ i = 1 N α i ∗ y i K ( x i , x ) + ( y j − ∑ i = 1 N α i ∗ y i K ( x i , x j ) ) = 0 决策函数 f ( x ) = s i g n [ ∑ i = 1 N α i ∗ y i K ( x i , x ) + ( y j − ∑ i = 1 N α i ∗ y i K ( x i , x j ) ) ] \begin{cases} \sum\limits_{i=1}^N\alpha_i^*y_i K(x_i,x)+\left(y_j-\sum\limits_{i=1}^N\alpha_i^*y_iK(x_i,x_j)\right)=0\\ 决策函数f(x)=sign\left[\sum\limits_{i=1}^N\alpha_i^*y_iK(x_i,x)+\left(y_j-\sum\limits_{i=1}^N\alpha_i^*y_iK(x_i,x_j)\right)\right] \end{cases} ⎩ ⎨ ⎧i=1∑Nαi∗yiK(xi,x)+(yj−i=1∑Nαi∗yiK(xi,xj))=0决策函数f(x)=sign[i=1∑Nαi∗yiK(xi,x)+(yj−i=1∑Nαi∗yiK(xi,xj))]
所以问题的关键为 如何确定核函数 K ( x i , x j ) K(x_i,x_j) K(xi,xj)
5.4.2 正定核函数
对于内积运算,
( x , x ) > 0 ,当 x > 0 时 ——正定性 ( x i , x j ) = ( x j , x i ) ——非负性 } ⇒ 正定核 \left. \begin{aligned} (x,x)>0,当x>0时&——正定性\\ (x_i,x_j)=(x_j,x_i)&——非负性 \end{aligned} \right\}\Rightarrow 正定核 (x,x)>0,当x>0时(xi,xj)=(xj,xi)——正定性——非负性}⇒正定核
故正定核函数应满足:
-
对称性: K ( x , z ) = K ( z , x ) K(x,z)=K(z,x) K(x,z)=K(z,x)
-
正定性: ∀ x 1 , x 2 ⋯ , x N ∈ R n \forall x_1,x_2\cdots,x_N\in R^n ∀x1,x2⋯,xN∈Rn , K ( x i , x j ) K(x_i,x_j) K(xi,xj) 的Gram阵是半正定的
-
Gram阵
原 [ ( x 1 , x 1 ) ⋯ ( x 1 , x N ) ⋮ ⋱ ⋮ ( x N , x 1 ) ⋯ ( x N , x N ) ] 新 [ K ( x 1 , x 1 ) ⋯ K ( x 1 , x N ) ⋮ ⋱ ⋮ K ( x N , x 1 ) ⋯ K ( x N , x N ) ] 原\left[ \begin{matrix} (x_1,x_1)&\cdots&(x_1,x_N)\\ \vdots&\ddots&\vdots\\ (x_N,x_1)&\cdots&(x_N,x_N) \end{matrix} \right]\qquad 新\left[ \begin{matrix} K(x_1,x_1)&\cdots&K(x_1,x_N)\\ \vdots&\ddots&\vdots\\ K(x_N,x_1)&\cdots&K(x_N,x_N) \end{matrix} \right] 原 (x1,x1)⋮(xN,x1)⋯⋱⋯(x1,xN)⋮(xN,xN) 新 K(x1,x1)⋮K(xN,x1)⋯⋱⋯K(x1,xN)⋮K(xN,xN) -
半正定
对于A, ∀ x ≠ 0 \forall x\neq 0 ∀x=0 ,有 x T A x ≥ 0 x^TAx\ge 0 xTAx≥0 ,则有A为半正定阵
半正定判定 { x T A x = y T D y —— D 为对角阵 全部特根 λ ≥ 0 所有主子行列式 ≥ 0 \begin{cases} x^TAx=y^TDy——D为对角阵\\ 全部特根\lambda\ge 0\\ 所有主子行列式\ge 0 \end{cases} ⎩ ⎨ ⎧xTAx=yTDy——D为对角阵全部特根λ≥0所有主子行列式≥0
-
由 K ( x , z ) K(x,z) K(x,z) 构造 H \mathcal{H} H 空间
任何一个核函数都隐式定义了一个成为 再生核希尔伯特空间 的特征空间
欧式空间 { 空间 ( 集合 ) → 元素是向量 向量空间 ⊆ 线性空间 ( 元素 + 数乘 ∈ 空间 ) → 内积 内积空间 { 表示向量间关系 用夹角表示,用 ( a , b ) 度量夹角大小 → 范数 赋范线性空间——表示向量大小、长度 数列存在极限且 ∈ 空间,任一柯西列都是收敛列 { x 1 ⋯ , x N } { x 1 > x 2 > ⋯ > x N 且 x 1 − x 2 > x 2 − x 3 > ⋯ > x N − 1 − x N ( 柯西列 ) → 0 ↓ 巴拿赫空间 \begin{aligned} &欧式空间&\begin{cases} 空间(集合)\xrightarrow{元素是向量}向量空间\subseteq 线性空间(元素+数乘\in 空间)\\ \xrightarrow{内积}内积空间\begin{cases} 表示向量间关系\\ 用夹角表示,用(a,b)度量夹角大小 \end{cases}\\ \xrightarrow{范数}赋范线性空间——表示向量大小、长度 \end{cases}\\ &&数列存在极限且\in 空间,任一柯西列都是收敛列\{x_1\cdots,x_N\}\\ &&\begin{cases} x_1>x_2>\cdots>x_N\\ 且x_1-x_2>x_2-x_3>\cdots>x_{N-1}-x_N(柯西列)\rightarrow 0\ \end{cases}\\ &\downarrow\\ &巴拿赫空间 \end{aligned} 欧式空间↓巴拿赫空间⎩ ⎨ ⎧空间(集合)元素是向量向量空间⊆线性空间(元素+数乘∈空间)内积内积空间{表示向量间关系用夹角表示,用(a,b)度量夹角大小范数赋范线性空间——表示向量大小、长度数列存在极限且∈空间,任一柯西列都是收敛列{x1⋯,xN}{x1>x2>⋯>xN且x1−x2>x2−x3>⋯>xN−1−xN(柯西列)→0
对于非欧氏空间上的完备空间,称为希尔伯特空间 H \mathcal{H} H
步骤
1. 定义映射
ϕ : x → K ( ⋅ , x ) \phi:x\rightarrow K(\cdot,x) ϕ:x→K(⋅,x)
- ⋅ \cdot ⋅ 表示任一位置元素
- ϕ ( ⋅ ) ⋅ ϕ ( x ) = K ( ⋅ , x ) \phi(\cdot)\cdot \phi(x)=K(\cdot,x) ϕ(⋅)⋅ϕ(x)=K(⋅,x) 表示 ϕ ( x ) \phi(x) ϕ(x) 与任一个元素的内积为 K ( ⋅ , x ) K(\cdot,x) K(⋅,x)
表示这个映射受核函数约束
线性组合: f ( ⋅ ) = ∑ i = 1 m α i K ( ⋅ , x i ) f(\cdot)=\sum\limits_{i=1}^m\alpha_iK(\cdot,x_i) f(⋅)=i=1∑mαiK(⋅,xi) ——向量
S = { f ( ⋅ ) } ——向量空间 S=\{f(\cdot)\}——向量空间 S={f(⋅)}——向量空间
2. S → + 内积 内积空间 S\xrightarrow{+内积}内积空间 S+内积内积空间
f ( ⋅ ) = ∑ i = 1 m α i K ( ⋅ , x i ) g ( ⋅ ) = ∑ j = 1 l β j ( ⋅ , z j ) } ⇒ f ⋅ g = ∑ i = 1 m ∑ j = 1 l α i β j K ( x i , z j ) \left.\begin{aligned} f(\cdot)=\sum\limits_{i=1}^m\alpha_iK(\cdot,x_i)\\ g(\cdot)=\sum\limits_{j=1}^l\beta_j(\cdot,z_j)\\ \end{aligned} \right\}\Rightarrow f\cdot g=\sum\limits_{i=1}^m\sum\limits_{j=1}^l\alpha_i\beta_jK(x_i,z_j) f(⋅)=i=1∑mαiK(⋅,xi)g(⋅)=j=1∑lβj(⋅,zj)⎭ ⎬ ⎫⇒f⋅g=i=1∑mj=1∑lαiβjK(xi,zj)
证明:
f ⋅ f ≥ 0 f ⋅ f = ∑ i = 1 m ∑ j = 1 m α i α j K ( x i , x j ) ≥ 0 令 x = ( α 1 , ⋯ , α m ) T , G = [ K ( x 1 , x 1 ) ⋯ K ( x 1 , x m ) ⋮ ⋱ ⋮ K ( x m , x 1 ) ⋯ K ( x m , x m ) ] x T G x = ( α 1 , ⋯ , α m ) G ( α 1 , ⋯ , α m ) T = [ α 1 K ( x 1 , x 1 ) + α 2 K ( x 2 , x 1 ) + ⋯ + α m K ( x m , x 1 ) ⋮ α 1 K ( x 1 , x m ) + α 2 K ( x 2 , x m ) + ⋯ + α m K ( x m , x m ) ] ( α 1 , ⋯ , α m ) T = ∑ i = 1 m ∑ j = 1 m α i α j K ( x i , x j ) ≥ 0 \begin{aligned} &f\cdot f\ge 0\\ &f\cdot f=\sum\limits_{i=1}^m\sum\limits_{j=1}^m\alpha_i\alpha_jK(x_i,x_j)\ge 0\\ &令x=(\alpha_1,\cdots,\alpha_m)^T,G=\left[ \begin{matrix} K(x_1,x_1)&\cdots&K(x_1,x_m)\\ \vdots&\ddots&\vdots\\ K(x_m,x_1)&\cdots&K(x_m,x_m) \end{matrix} \right]\\ &\begin{aligned} x^TGx&=(\alpha_1,\cdots,\alpha_m)G(\alpha_1,\cdots,\alpha_m)^T\\ &=\left[ \begin{matrix} \alpha_1K(x_1,x_1)+\alpha_2K(x_2,x_1)+\cdots+\alpha_mK(x_m,x_1)\\ \vdots\\ \alpha_1K(x_1,x_m)+\alpha_2K(x_2,x_m)+\cdots+\alpha_mK(x_m,x_m)\\ \end{matrix} \right](\alpha_1,\cdots,\alpha_m)^T\\ &=\sum\limits_{i=1}^m\sum\limits_{j=1}^m\alpha_i\alpha_jK(x_i,x_j)\ge 0 \end{aligned} \end{aligned} f⋅f≥0f⋅f=i=1∑mj=1∑mαiαjK(xi,xj)≥0令x=(α1,⋯,αm)T,G= K(x1,x1)⋮K(xm,x1)⋯⋱⋯K(x1,xm)⋮K(xm,xm) xTGx=(α1,⋯,αm)G(α1,⋯,αm)T= α1K(x1,x1)+α2K(x2,x1)+⋯+αmK(xm,x1)⋮α1K(x1,xm)+α2K(x2,xm)+⋯+αmK(xm,xm) (α1,⋯,αm)T=i=1∑mj=1∑mαiαjK(xi,xj)≥0
3. S → + 范数 赋范空间 → 完备化 H S\xrightarrow{+范数}赋范空间\xrightarrow{完备化}\mathcal{H} S+范数赋范空间完备化H
再生性
K ( ⋅ , x ) ⋅ K ( ⋅ , z ) = K ( x , z ) f ( ⋅ ) = ∑ i α i K ( ⋅ , x i ) K ( ⋅ , x ) f ( ⋅ ) = ∑ i α i K ( x , x i ) = f ( x ) K(\cdot,x)\cdot K(\cdot,z)=K(x,z)\\ f(\cdot)=\sum\limits_{i}\alpha_iK(\cdot,x_i)\\ K(\cdot,x)f(\cdot)=\sum\limits_{i}\alpha_i K(x,x_i)=f(x) K(⋅,x)⋅K(⋅,z)=K(x,z)f(⋅)=i∑αiK(⋅,xi)K(⋅,x)f(⋅)=i∑αiK(x,xi)=f(x)
常用核函数
在支持向量机中,核函数的选择是一个核心问题,常用核函数有:
线性核 : K ( X , Y ) = X T Y K(X,Y)=X^TY K(X,Y)=XTY
多项式核 : K ( X , Y ) = ( X T Y + c ) d K(X,Y)=(X^TY+c)^d K(X,Y)=(XTY+c)d , c c c 为常数, d ≥ 1 d\ge 1 d≥1 为多项式次数
高斯核 : K ( X , Y ) = e − ∥ X − Y ∥ 2 2 σ 2 K(X,Y)=e^{-\frac{\Vert X-Y\Vert^2}{2\sigma^2}} K(X,Y)=e−2σ2∥X−Y∥2 , σ > 0 \sigma>0 σ>0 为高斯核带宽
拉普拉斯核 : K ( X , Y ) = e − ∥ X − Y ∥ σ K(X,Y)=e^{-\frac{\Vert X-Y\Vert}{\sigma}} K(X,Y)=e−σ∥X−Y∥
sigmod核 : K ( X , Y ) = t a n h ( β X T Y + θ ) K(X,Y)=tanh(\beta X^TY+\theta) K(X,Y)=tanh(βXTY+θ) , β > 0 \beta >0 β>0 , θ < 0 \theta <0 θ<0
5.5 SVM参数求解算法
将支持向量机的最优化作为原始问题,应用最优化理论中的拉格朗日对偶性,可以通过求解其对偶问题得到原始问题的最优解
SVM关键是如何根据支持向量构建解,算法的复杂度也主要取决于支持向量的数目
在算法实现过程中,支持向量机会遇到大量训练样本下,全局最优解难以求得的情况——SMO算法(序列最小最优化)
支持向量机的学习问题可以形式化为凸二次规划问题的求解,SMO算法的特点是不断将原始的二次规划问题分解为只有两个变量的二次规划子问题,并求解子问题的解析解,直到所有变量满足条件为止
5.6 SVM与线性模型关系
逻辑斯蒂模型损失函数
J ( ω ) = − 1 n [ ∑ i = 1 n ∑ k = 1 2 I ( y i = k ) ln P ( y i = k ∣ x i , ω ) ] = − 1 n [ ∑ i = 1 n y i ln P ( y i = 1 ∣ x i , ω ) + ( 1 − y i ) ln P ( y i = 0 ∣ x i , ω ) ] \begin{aligned} J(\omega)&=-\frac{1}{n}\left[\sum\limits_{i=1}^n\sum\limits_{k=1}^2I(y_i=k)\ln P(y_i=k\vert x_i,\omega)\right]\\ &=-\frac{1}{n}\left[\sum\limits_{i=1}^ny_i\ln P(y_i=1\vert x_i,\omega)+(1-y_i)\ln P(y_i=0\vert x_i,\omega)\right] \end{aligned} J(ω)=−n1[i=1∑nk=1∑2I(yi=k)lnP(yi=k∣xi,ω)]=−n1[i=1∑nyilnP(yi=1∣xi,ω)+(1−yi)lnP(yi=0∣xi,ω)]
正则化
J ( ω ) + λ 2 n ∥ ω ∥ 2 2 J(\omega)+\frac{\lambda}{2n}\Vert \omega\Vert_2^2 J(ω)+2nλ∥ω∥22
即逻辑斯蒂模型先有损失函数,再做正则化
SVM:将损失函数作为约束,先求出参数,再以损失函数为约束
相关文章:

【AI】机器学习——支持向量机(非线性及分析)
5. 支持向量机(线性SVM) 文章目录 5.4 非线性可分SVM5.4.1 非线性可分问题处理思路核技巧核函数特点 核函数作用于SVM 5.4.2 正定核函数由 K ( x , z ) K(x,z) K(x,z) 构造 H \mathcal{H} H 空间步骤 常用核函数 5.5 SVM参数求解算法5.6 SVM与线性模型关系 5.4 非线性可分SVM …...
2023-09-20 LeetCode每日一题(拿硬币)
2023-09-20每日一题 一、题目编号 LCP 06. 拿硬币二、题目链接 点击跳转到题目位置 三、题目描述 桌上有 n 堆力扣币,每堆的数量保存在数组 coins 中。我们每次可以选择任意一堆,拿走其中的一枚或者两枚,求拿完所有力扣币的最少次数。 示…...
Java21的新特性
Java语言特性系列 Java5的新特性Java6的新特性Java7的新特性Java8的新特性Java9的新特性Java10的新特性Java11的新特性Java12的新特性Java13的新特性Java14的新特性Java15的新特性Java16的新特性Java17的新特性Java18的新特性Java19的新特性Java20的新特性Java21的新特性Java22…...
测试-----selenuim webDriver
文章目录 1.页面导航2.元素定位3. 浏览器操作4.获取元素信息5. 鼠标的操作6. 键盘操作7. 元素等待8.下拉框9.弹出框10.滚动条11.frame处理12.验证码处理(cookie) 1.页面导航 首先是导入对应的包 :from selenium import webdriver然后实例化:driver web…...

21天学会C++:Day12----初始化列表
CSDN的uu们,大家好。这里是C入门的第十一讲。 座右铭:前路坎坷,披荆斩棘,扶摇直上。 博客主页: 姬如祎 收录专栏:C专题 目录 1. 初始化列表 1.1 引入 1.2 初始化列表 1.3 初始化列表的注意事项 1.…...
OpenAI开发系列(二):大语言模型发展史及Transformer架构详解
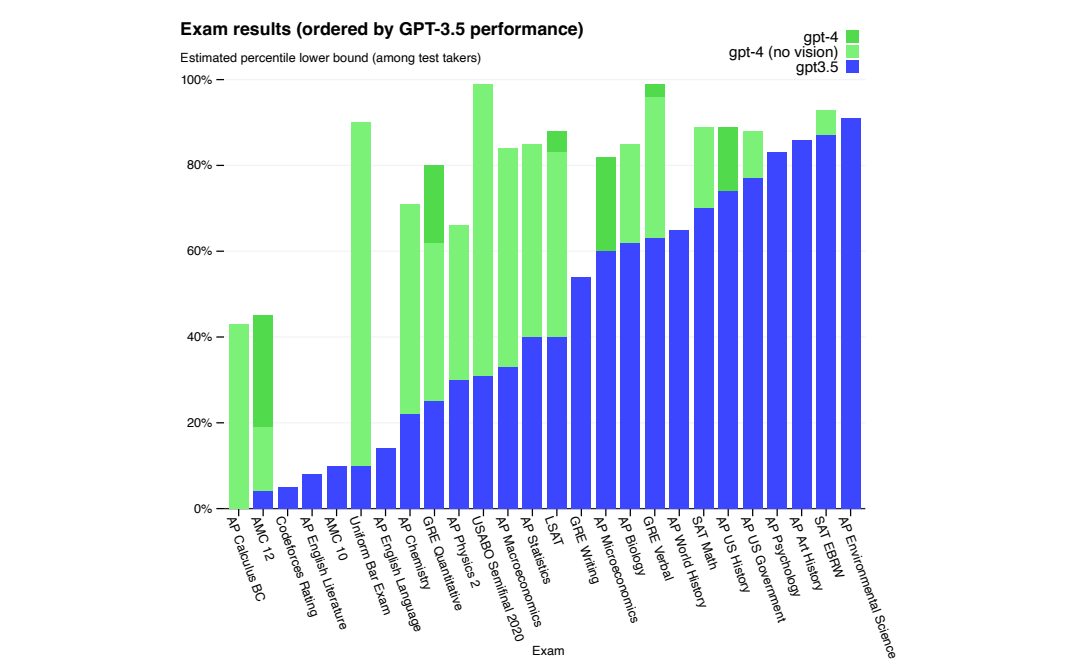
全文共1.8w余字,预计阅读时间约60分钟 | 满满干货,建议收藏! 一、介绍 在2020年秋季,GPT-3因其在社交媒体上病毒式的传播而引发了广泛关注。这款拥有超过1.75亿参数和每秒运行成本达到100万美元的大型语言模型(Large …...

Gson - 一个Java序列化/反序列化库
官网 GitHub - google/gson: A Java serialization/deserialization library to convert Java Objects into JSON and back 项目简介 一个Java序列化/反序列化库,用于将Java对象转换为JSON和返回JSON。 Gson is a Java library that can be used to convert Java…...
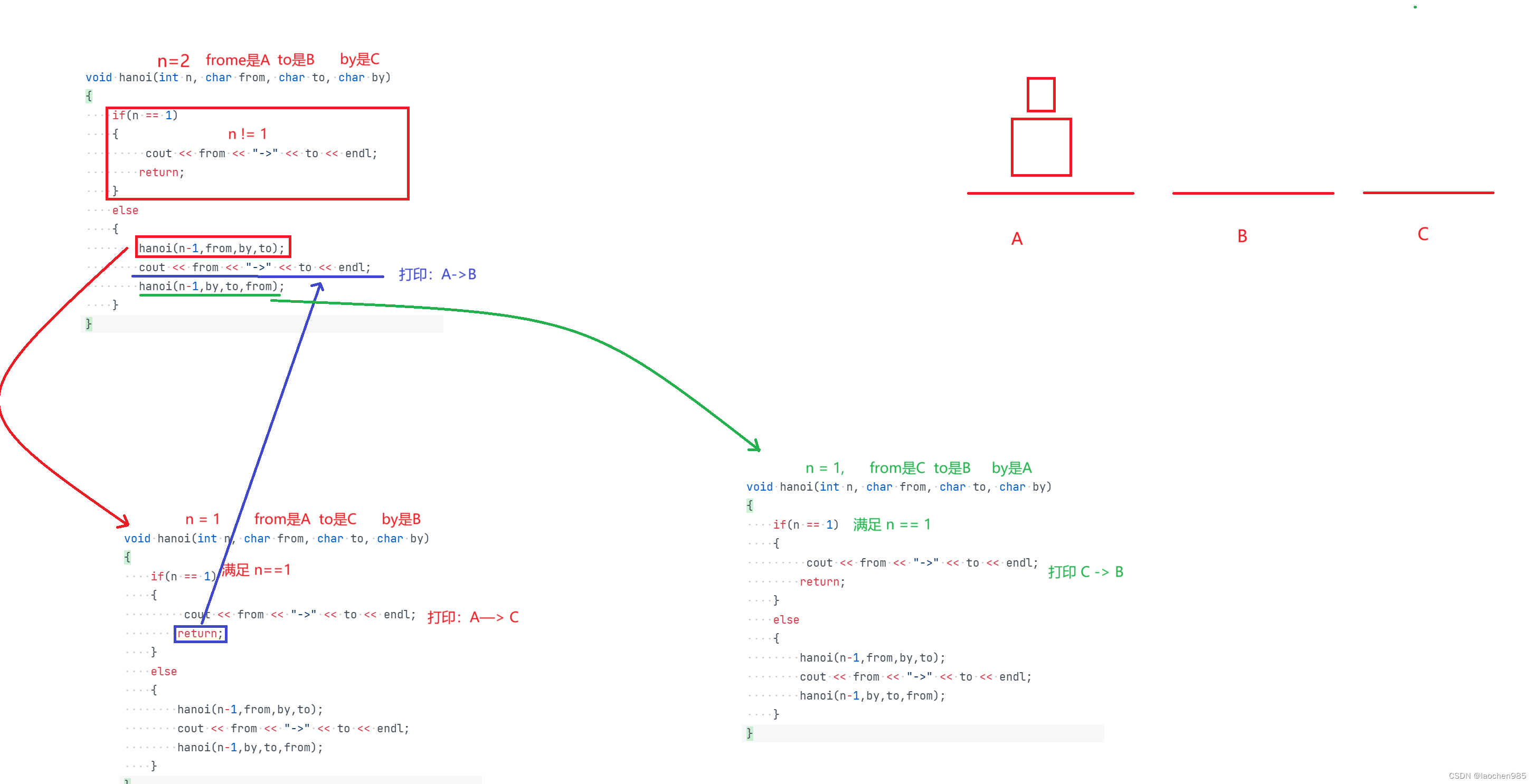
6-1 汉诺塔
汉诺(Hanoi)塔问题是一个经典的递归问题。 设有A、B、C三个塔座;开始时,在塔座A上有若干个圆盘,这些圆盘自下而上,由大到小地叠在一起。要求将塔座A上的圆盘移到塔座B上,并仍按同样顺序叠放。在…...
添加密码登录验证)
Linux之initd管理系统(海思、ZYNQ、复旦微)添加密码登录验证
设置root用户密码:passwd命令设置密码,即修改/etc/passwd文件 一、串口提示输入用户名密码方法 修改 /etc/inittab 方法一: 增加: ::askfirst:-/bin/login 注释: #::respawn:/sbin/getty -L ttyS000 115200 vt…...
怎么更改代理ip,代理ip如何切换使用?
我们要如何使用HTTP代理,对它进行切换使用呢? 如果你购买了青果网络的HTTP代理,可以在文档这边获取使用方法: 可以在这里调试: 也可以在这里选择key提取。 如果有的朋友们想利用利用python,每隔30秒使用API…...
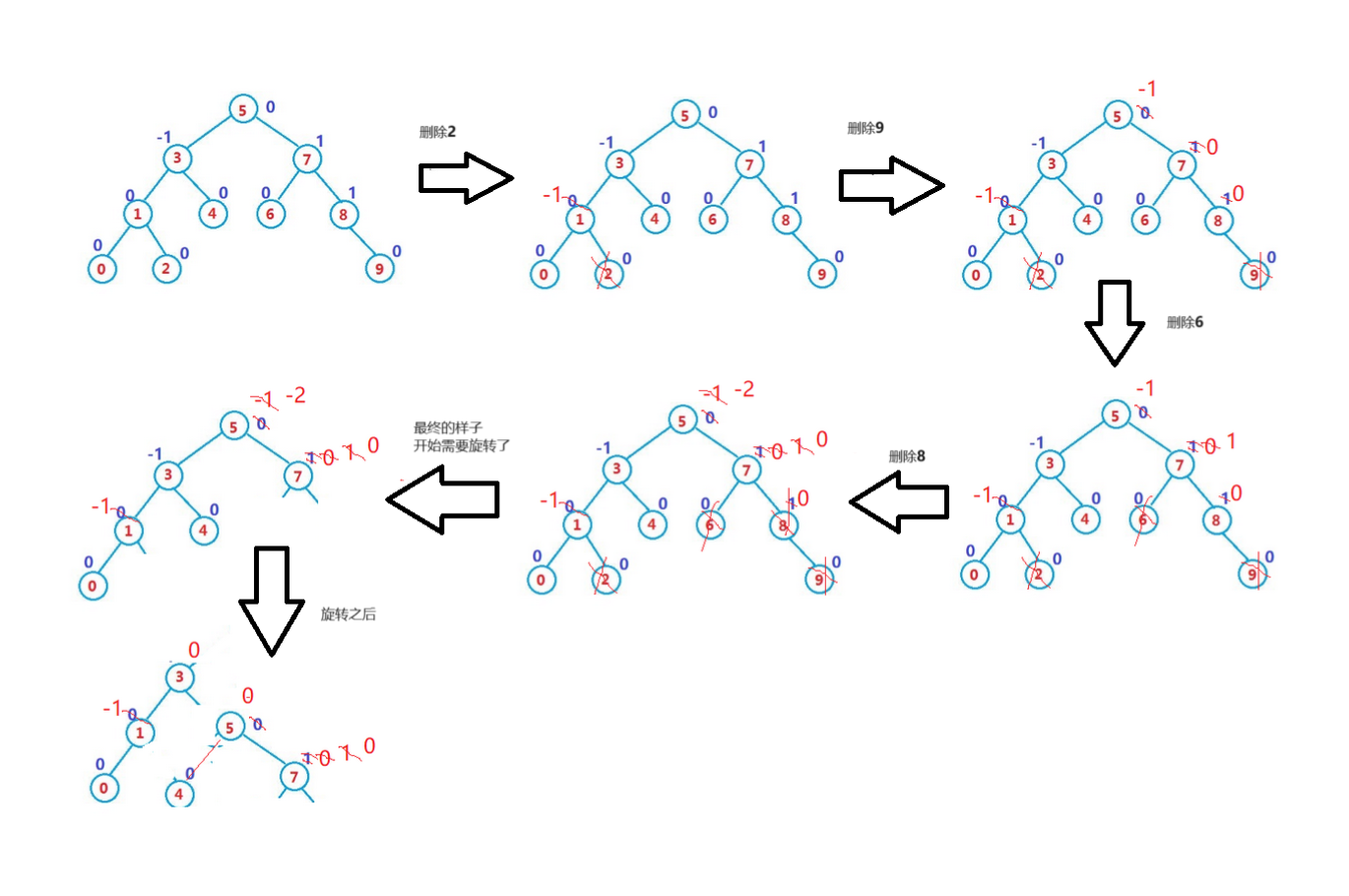
【C++从0到王者】第三十三站:AVL树
文章目录 前言一、AVL 树的概念二、AVL树的实现1. AVL树的结点定义2. AVL树的插入之插入部分3. AVL树的插入之平衡因子的改变4. AVL树的插入之左旋5. AVL树的左旋抽象图6.AVL树的右旋抽象图7. AVL树的双旋8. AVL树的右左双旋9. AVL树的右左双旋的本质10. AVL树的左右双旋11. AV…...

手机机型响应式设置2
window.screen.height:屏幕高度 window.innerHeight:视口高度(去除浏览器头尾的高度) document.body.clientHeight:内容高度 vh:网页视口高度的1/100 vw:网页视口宽度的1/100 vmaxÿ…...

uni-app 之 解决u-button始终居中问题
uView中u-button始终居中问题如何解决的简单方法? 1:给该元素margin-right: 0;可以达到向右靠齐; 2:给该元素的父元素设置float: right image.png <u-button style"width: 50px; margin-left: 0;" plain"t…...

Python日期处理库:掌握时间的艺术
💂 个人网站:【工具大全】【游戏大全】【神级源码资源网】🤟 前端学习课程:👉【28个案例趣学前端】【400个JS面试题】💅 寻找学习交流、摸鱼划水的小伙伴,请点击【摸鱼学习交流群】 日期和时间在计算机编程…...

JOSEF约瑟 智能电流继电器KWJL-20/L KWLD26 零序孔径45mm 柜内导轨式安装
KWJL-20智能电流继电器 零序互感器: KWLD80 KWLD45 KWLD26 KWJL-20 一、产品概述 KWJL-20系列智能剩余电流继电器(以下简称继电器)适用于交流电压至660V或更高的TN、TT、和IT系统,频率为50Hz。通过零序电流互感器检测出超过…...

NLP技术如何为搜索引擎赋能
目录 1. NLP关键词提取与匹配在搜索引擎中的应用1. 关键词提取例子 2. 关键词匹配例子 Python实现 2. NLP语义搜索在搜索引擎中的应用1. 语义搜索的定义例子 2. 语义搜索的重要性例子 Python/PyTorch实现 3. NLP个性化搜索建议在搜索引擎中的应用1. 个性化搜索建议的定义例子 2…...

演唱会没买到票?VR直播为你弥补遗憾
听说周杰伦开了演唱会?没买到票的人是不是有着大大的遗憾呢?很多时候大型活动、演唱会都会因为场地限制而导致很多人未能有缘得见,而且加上票价成本高,“黄牛票”事件频出,我们的钱包受不住啊!!…...

myabtis的缓存级别
文章目录 MyBatis缓存的区别是什么作用范围方面有哪些差异生命周期数据进行了存储缓存的优缺点 MyBatis缓存的区别是什么 MyBatis 提供了一级缓存和二级缓存,这两者的主要区别在于其作用范围和生命周期。 一级缓存:一级缓存是 SqlSession 级别的缓存。…...
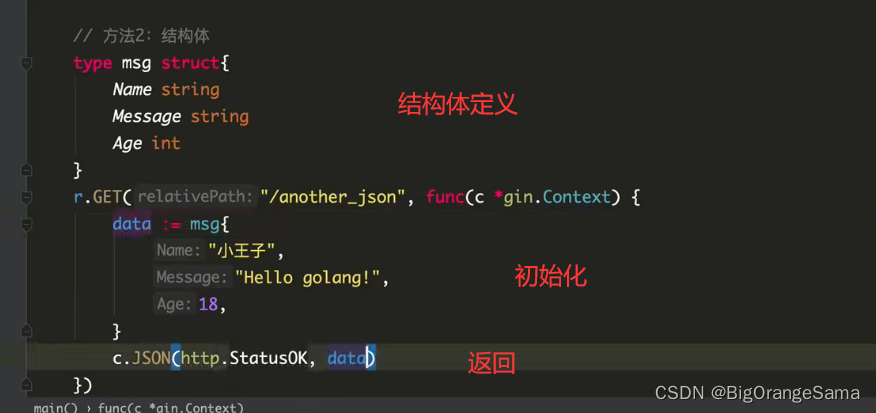
gin框架再探
Gin框架介绍及使用 | 李文周的博客 (liwenzhou.com) lesson03_gin框架初识_哔哩哔哩_bilibili 1.路由引擎 //路由引擎 rgin.Default() 2.一些http请求方法 get post put delete等等 遇到什么路径,执行什么函数 r.GET("/hello",func{做你想做的事返回…...

经典算法-----约瑟夫问题(C语言)
目录 前言 故事背景 约瑟夫问题 环形链表解决 数组解决 前言 今天我们来玩一个有意思的题目,也就是约瑟夫问题,这个问题出自于欧洲中世纪的一个故事,下面我们就去通过编程的方式来解决这个有趣的问题,一起来看看吧!…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
