LeetCode 2097. 合法重新排列数对【欧拉通路,DFS】2650
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个下标从 0 开始的二维整数数组 pairs ,其中 pairs[i] = [starti, endi] 。如果 pairs 的一个重新排列,满足对每一个下标 i ( 1 <= i < pairs.length )都有 endi-1 == starti ,那么我们就认为这个重新排列是 pairs 的一个 合法重新排列 。
请你返回 任意一个 pairs 的合法重新排列。
注意: 数据保证至少存在一个 pairs 的合法重新排列。
示例 1:
输入:pairs = [[5,1],[4,5],[11,9],[9,4]]
输出:[[11,9],[9,4],[4,5],[5,1]]
解释:
输出的是一个合法重新排列,因为每一个 endi-1 都等于 starti 。
end0 = 9 == 9 = start1
end1 = 4 == 4 = start2
end2 = 5 == 5 = start3
示例 2:
输入:pairs = [[1,3],[3,2],[2,1]]
输出:[[1,3],[3,2],[2,1]]
解释:
输出的是一个合法重新排列,因为每一个 endi-1 都等于 starti 。
end0 = 3 == 3 = start1
end1 = 2 == 2 = start2
重新排列后的数组 [[2,1],[1,3],[3,2]] 和 [[3,2],[2,1],[1,3]] 都是合法的。
示例 3:
输入:pairs = [[1,2],[1,3],[2,1]]
输出:[[1,2],[2,1],[1,3]]
解释:
输出的是一个合法重新排列,因为每一个 endi-1 都等于 starti 。
end0 = 2 == 2 = start1
end1 = 1 == 1 = start2
提示:
1 <= pairs.length <= 10^5pairs[i].length == 20 <= starti, endi <= 10^9starti != endipairs中不存在一模一样的数对。- 至少 存在 一个合法的
pairs重新排列。
解法 欧拉路径+DFS
如果我们把数组 p a i r s pairs pairs 中出现的每个数看成一个节点, ( start i , end i ) (\textit{start}_i, \textit{end}_i) (starti,endi) 看成从 start i \textit{start}_i starti 到 end i \textit{end}_i endi 的一条有向边,那么 p a i r s pairs pairs 的一个合法排列就对应着:
- 从节点 pairs [ 0 ] [ 0 ] \textit{pairs}[0][0] pairs[0][0] 开始;
- 依次经过 pairs [ 0 ] [ 1 ] , pairs [ 1 ] [ 1 ] , ⋯ , pairs [ n − 1 ] [ 1 ] \textit{pairs}[0][1], \textit{pairs}[1][1], \cdots, \textit{pairs}[n-1][1] pairs[0][1],pairs[1][1],⋯,pairs[n−1][1]
的一条路径,其中 n n n 是数组 p a i r s pairs pairs 的长度。这条路径经过了图上的每一条边恰好一次,是一条「欧拉通路」,因此我们的目标就是找出图上的任意一条欧拉通路。
对于本题而言,首先需要找到欧拉通路的起始节点:
- 如果图中所有节点的入度和出度都相等,那么从任意节点开始都存在欧拉通路;
- 如果图中存在一个节点的出度比入度恰好多 1 1 1 ,另一个节点的入度恰好比出度多 1 1 1 ,那么欧拉通路必须从前一个节点开始,到后一个节点结束。
- 除此之外的有向图都不存在欧拉通路。
本题保证了至少存在一个合法排列,因此图已经是上述的两种情况之一。当我们确定起始节点后,就可以使用DFS求解欧拉通路了。如果我们得到的欧拉通路为:
v 1 , v 2 , v 3 , ⋯ , v n , v n + 1 v_1, v_2, v_3, \cdots, v_n, v_{n+1} v1,v2,v3,⋯,vn,vn+1
那么 [ [ v 1 , v 2 ] , [ v 2 , v 3 ] , ⋯ , [ v n , v n + 1 ] ] [[v_1, v_2], [v_2, v_3], \cdots, [v_n, v_{n+1}]] [[v1,v2],[v2,v3],⋯,[vn,vn+1]] 就是一个合法排列。
class Solution {
public:vector<vector<int>> validArrangement(vector<vector<int>>& pairs) {// 存储图unordered_map<int, vector<int>> edges;// 存储入度和出度unordered_map<int, int> deg;for (const auto& p: pairs) {edges[p[0]].push_back(p[1]);++deg[p[0]], --deg[p[1]];}// 深度优先搜索(Hierholzer算法)求解欧拉通路vector<vector<int>> ans;function<void(int)> dfs = [&](int u) {while (!edges[u].empty()) {int v = edges[u].back();edges[u].pop_back(); // 删除一条边dfs(v);ans.push_back({u, v});}}; // 寻找起始节点for (const auto& [x, occ]: deg) // 如果有节点出度比入度恰好多 1,那么只有它才能是起始节点if (occ == 1) {dfs(x);break;}if (ans.empty()) dfs(pairs[0][0]);reverse(ans.begin(), ans.end());return ans;}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) ,其中 nnn 是数组 p a i r s pairs pairs 的长度。图中有不超过 n + 1 n+1 n+1 个节点和 n n n 条边,因此求解欧拉通路需要的时间为 O ( n ) O(n) O(n) 。
- 空间复杂度: O ( n ) O(n) O(n) ,即为存储图需要使用的空间。
求解欧拉通路使用DFS,可以参考「OI Wiki — 欧拉图」 ,一般使用 Hierholzer \text{Hierholzer} Hierholzer 算法求解欧拉通路,与欧拉回路或欧拉通路有关的题目:
- 「332. 重新安排行程」
- 「753. 破解保险箱」
相关文章:

LeetCode 2097. 合法重新排列数对【欧拉通路,DFS】2650
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
学习笔记-接口测试(postman、jmeter)
目录 一、什么是接口测试 二、前端和后端 三、get请求和post请求的区别 四、cookie和session 五、接口测试的依据 六、HTTP状态码 七、通用接口用例 八、postman接口测试 九、Jmeter接口测试 一、什么是接口测试 通常做的接口测试指的是系统对外的接口,比…...
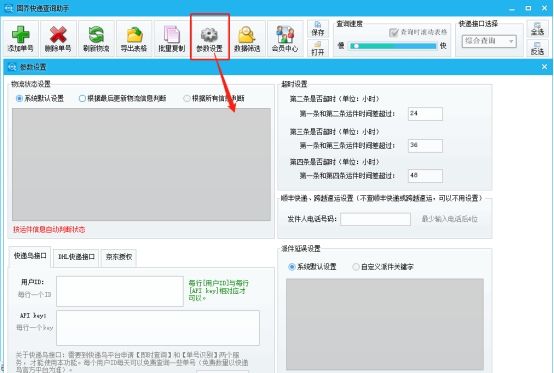
如何高效批量查询快递单号,提高工作效率?
在日常生活中,快递单号的查询是一项常规任务。过去,这项任务需要通过人工一个一个地在快递平台上查询,既耗时又费力。然而,随着科技的发展,我们有了更多的工具可以帮助我们高效地完成这项任务。本文将介绍如何使用固乔…...

12万汉语源流词典汉字记性ACCESS\EXCEL数据库
《12万汉语源流词典汉字记性ACCESS数据库》在继承前人经验的基础上,注意吸收今人的研究成果,注重形音义的密切配合,尽可能历史地、正确地反映汉字形音义的发展。在字形方面,简要说明其结构的演变。语义解释遵循古今语义的发展变化…...

深度解剖数据在队列的应用
> 作者简介:დ旧言~,目前大一,现在学习Java,c,c,Python等 > 座右铭:松树千年终是朽,槿花一日自为荣。 > 望小伙伴们点赞👍收藏✨加关注哟💕…...

IMX6ULL移植篇-Linux内核源码目录分析二
一. Linux内核源码目录 本文继续来具体说明 Linux内核源码的一些重要文件含义。 本文续上一篇文章,地址如下: IMX6ULL移植篇-Linux内核源码目录分析一_凌肖战的博客-CSDN博客 二. Linux内核源码目录分析 9. init 目录 此目录存放 Linux 内核启动的…...

汽车行业数据治理方案,助力车企研产供销数据一体化
随着数字技术的不断革新和应用,汽车行业已转向大数据、新技术寻求生产力突破,以电动化、网联化、智能化、共享化为标志的“汽车新四化”,为汽车行业带来了翻天覆地的变化。如何抓住“新四化”的机会,在汽车产业变革中赢得先机&…...
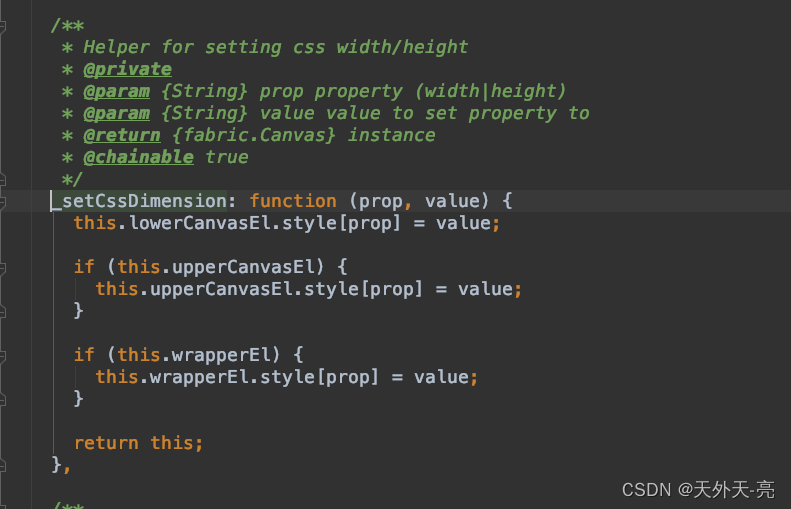
canvas-绘图库fabric.js简介
一般情况下简单的绘制,其实canvas原生方法也可以满足,比如画个线,绘制个圆形、正方形、加个文案。 let canvas document.getElementById(canvas);canvas.width 1200;canvas.height 600;canvas.style.width 1200px;canvas.style.height 6…...

代码审计——任意文件下载详解(二)
为方便您的阅读,可点击下方蓝色字体,进行跳转↓↓↓ 01 漏洞描述02 审计要点03 漏洞特征04 漏洞案例05 修复方案 01 漏洞描述 网站可能提供文件查看或下载的功能,如果对用户查看或下载的文件不做限制,就能够查看或下载任意的文件&…...

19异常的学习笔记
异常 很重要,有利于我们平时处理问题 异常就是代表程序出现了问题 常见的异常比如说 数组越界除法除0 异常的体系是什么 java.lang.Throwable Error Exception RuntimeException 其他异常 Error 代表的是系统级别的错误,也就是一旦系统出现问题&…...

Jenkins学习笔记4
配置构建流程: Jenkins任务创建: 1)创建新任务: 把这个Accept first connection改成 No Validation。问题得到解决。 构建触发器这块暂时没有需要配置的。 传输文件到nginx-server这个web服务器中。 将文件上传到/usr/share/n…...

自学 Java 需要具备哪些基本条件或技能?
新手初学者在自己学习Java时,需要注意两个方面,一个是学习方面,一个是知识点方面! 学习方面: 1、做学习计划并保持自律 在我们学习Java的过程中,尽量减少干扰,把自己的全部注意力集中在Java上…...
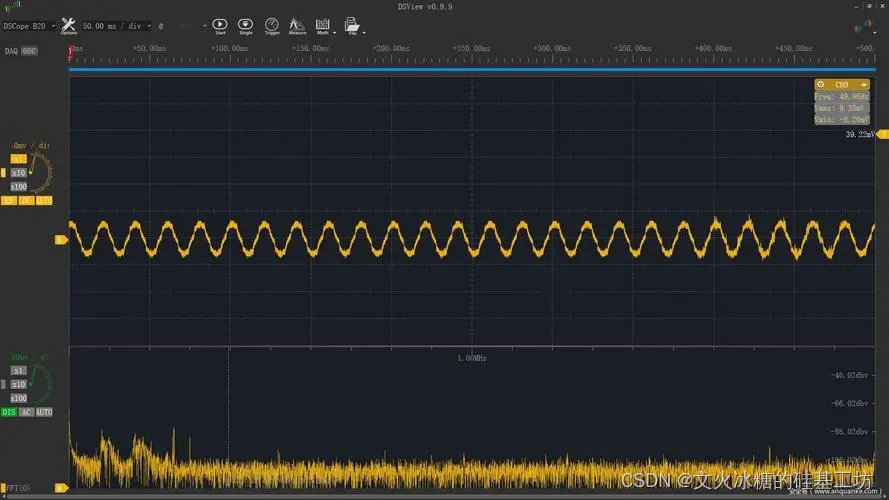
[激光原理与应用-68]:如何消除50Hz工频干扰和差分信号应对工频干扰
目录 一、什么工频干扰 1.1 什么工频干扰 1.2 工频干扰的幅度 1.3 工频干扰如何进入设备 1.4 工频干扰的负面影响 二、如何消除工频干扰 2.1 要消除工频干扰,可以考虑以下方法: 2.2 要具体消除工频干扰,可以采取以下措施 2.3 使用差…...
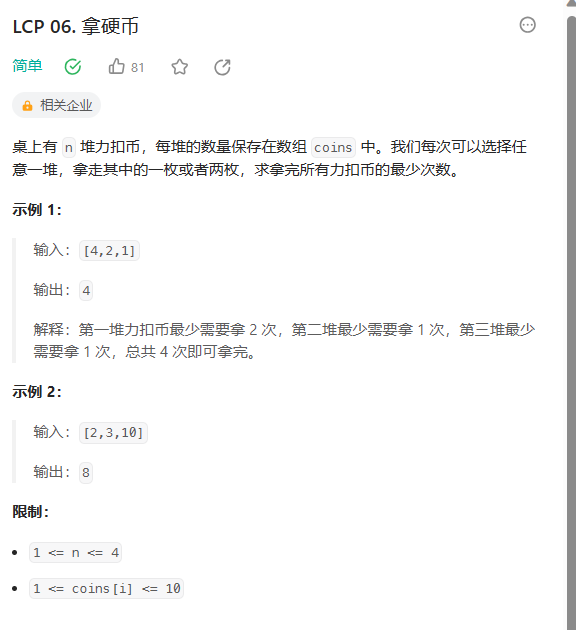
【力扣-每日一题】LCP 06. 拿硬币
class Solution { public:int minCount(vector<int>& coins) {int res0;for(auto i:coins){resi/2;res(i%2)?1:0;}return res;} };...

【JAVA-Day32】精通Java函数:定义、调用和主函数的完整指南
精通Java函数:定义、调用和主函数的完整指南 精通Java函数:定义、调用和主函数的完整指南摘要引言1. Java函数基础什么是Java函数?函数的定义和命名规则参数和返回值的概念 2. 函数的定义与语法如何声明和定义函数?函数的参数和参…...

springboot相关操作学习汇总
IDEAMAVEN apache maven 3.6.3 的安装及配置IntelliJ IDEA 安装及配置详细教程Maven下载安装及IDEA配置Maven的超详细教程 GIT 版本控制工具 - git的安装与使用gitlab上传新项目全过程 SPRINGBOOT IDEAmavenSpringboot工程创建超详细过程示例SpingBoot:整合Myb…...
如何在微信上制作自己的小程序卖东西
在当今的数字化时代,微信小程序已成为电商行业的重要平台。本文将详细解析电商微信小程序的制作流程,帮助你了解从零到上线的过程。 一、前期准备 1. 确定商城定位和目标群体:在制作电商微信小程序前,你需要明确商城的定位&#x…...
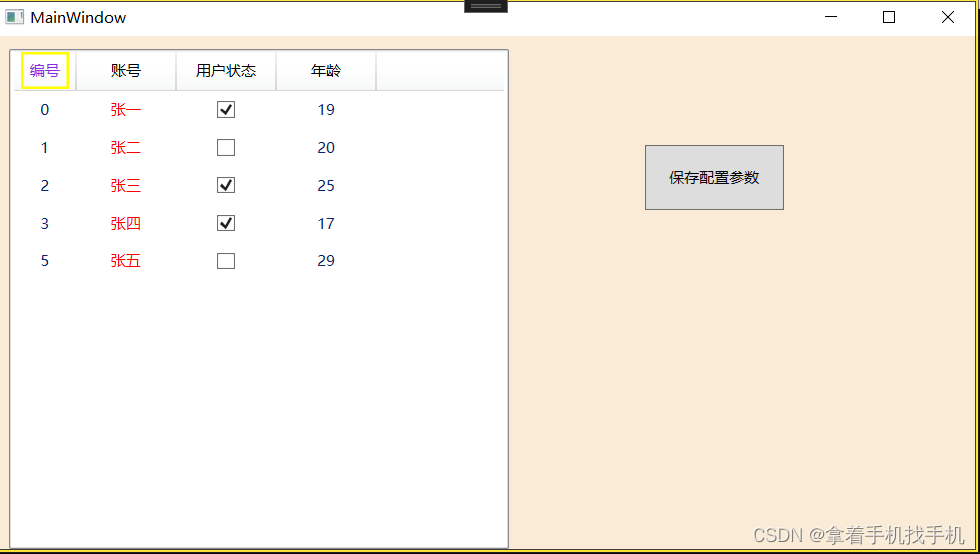
24.Xaml ListView控件-----显示数据
1.运行效果 2.运行源码 a.Xaml源码 <Window x:Class="testView.MainWindow"xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d="http://schemas.mic…...

YoloV5改进实战:使用MPDIoU改进YoloV5
文章目录 摘要论文:揭秘精准高效的MPDIoU损失函数摘要1、简介2、相关工作2.1、目标检测和实例分割2.2. 场景文本识别2.3、边界框回归的损失函数3、点距最小的并集交点4、实验结果4.1、 实验设置4.2、数据集4.3、 评估协议4.4、 目标检测的实验结果4.5、 字符级场景文本识别的实…...

从电大搜题到上海开放大学,广播电视大学引领学习新风尚
近年来,随着信息技术的飞速发展,互联网的普及和应用成为了我们生活中不可或缺的一部分。而在大学学习领域,电大搜题微信公众号应运而生,为广大学子提供了便捷的学习资源和交流平台。在这个信息高速发展的时代,上海开放…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
