卡尔曼滤波应用在数据处理方面的应用
卡尔曼滤波应用到交通领域
- 滤波器介绍
- 核心思想
- 核心公式
- 一维卡尔曼滤波器示例
- 导入所需的库
滤波器介绍
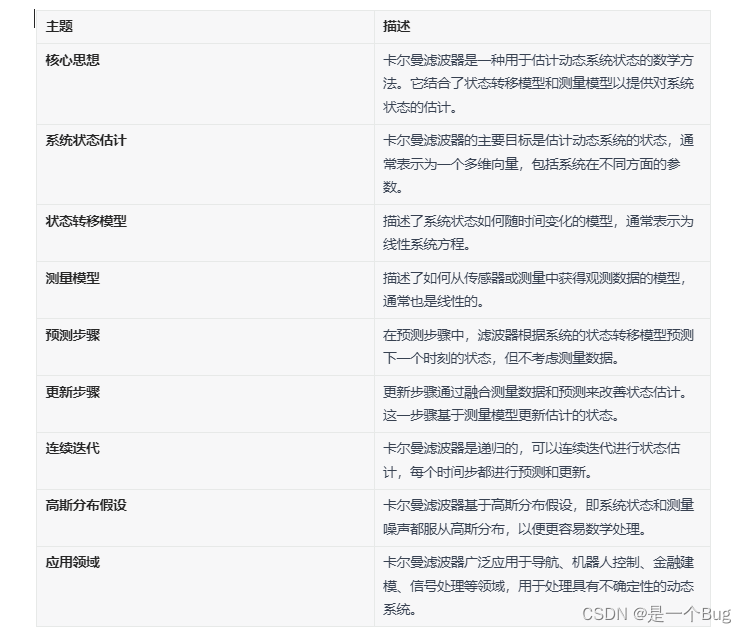
卡尔曼滤波器是一种用于估计系统状态的数学方法,它以卡尔曼核心思想为基础,广泛应用于估计动态系统的状态和滤除测量中的噪声。以下是卡尔曼滤波器的核心思想和介绍:
-
系统状态估计: 卡尔曼滤波器的主要目标是估计动态系统的状态,这个状态通常由一个多维向量表示,包含了系统在不同方面的参数。例如,可以用卡尔曼滤波器来估计飞机的位置、速度和方向,或者用来估计汽车的位置和速度等。
-
状态转移模型: 卡尔曼滤波器使用状态转移模型来描述系统状态如何随时间变化。这个模型通常表示为一个线性系统方程,它将当前时刻的状态与前一个时刻的状态以及系统的控制输入关联起来。状态转移模型描述了系统的动态行为。
-
测量模型: 卡尔曼滤波器还使用测量模型来描述如何从传感器或测量中获得观测数据。测量模型通常也是线性的,它将系统状态映射到观测数据的空间。测量模型告诉滤波器如何将系统状态与观测数据关联起来。
-
预测步骤: 卡尔曼滤波器的核心思想之一是预测步骤,它用于根据系统的状态转移模型预测下一个时刻的状态。在这一步骤中,滤波器估计系统的状态将如何变化,但尚未考虑测量数据。
-
更新步骤: 更新步骤是卡尔曼滤波器的另一个核心思想。在此步骤中,滤波器考虑到实际的测量数据,根据测量模型和当前的状态预测来更新状态估计。这个步骤通过融合测量数据和预测来改善状态估计的精确度。
-
连续迭代: 卡尔曼滤波器是一个递归滤波器,意味着它可以连续地迭代进行状态估计。在每个时间步中,滤波器都会进行预测和更新,从而不断改进对系统状态的估计。
-
高斯分布假设: 卡尔曼滤波器通常基于高斯分布假设,即系统的状态和测量噪声都服从高斯分布。这个假设使得卡尔曼滤波器在数学上更容易处理,但也限制了其适用性。
卡尔曼滤波器广泛应用于诸如导航、机器人控制、金融建模、信号处理等领域。它在处理具有不确定性和噪声的动态系统时非常有用,可以提供对系统状态的精确估计。然而,要成功应用卡尔曼滤波器,需要精确地建立状态转移模型和测量模型,并且要了解系统的特性和噪声。
核心思想
卡尔曼滤波的核心思想是通过融合两个来源的信息来估计动态系统的状态:1) 来自系统的先验信息(基于过去状态的预测),和 2) 来自传感器或测量的信息。它通过不断迭代的方式,通过预测和更新步骤来提高对系统状态的估计精度。
具体来说,卡尔曼滤波的核心思想可以概括为以下几点:
状态估计的不确定性管理: 卡尔曼滤波器维护对系统状态的估计以及估计的不确定性。状态估计通常表示为一个多维向量,而状态的不确定性则通过状态协方差矩阵来表示。
状态转移模型: 卡尔曼滤波器使用系统的状态转移模型来预测下一个时刻的状态。这个模型描述了系统状态如何随时间变化。
测量模型: 卡尔曼滤波器使用测量模型来将实际测量数据映射到状态空间。测量模型描述了如何从传感器或测量中获得观测数据。
预测步骤: 在预测步骤中,滤波器使用状态转移模型来预测下一个时刻的状态,但不考虑测量数据。这一步骤提供了先验估计和估计的不确定性。
更新步骤: 在更新步骤中,滤波器使用测量数据来校正先验估计,从而改善状态估计的精度。这一步骤考虑了测量模型和观测数据的不确定性。
连续迭代: 卡尔曼滤波器是递归的,可以连续迭代进行状态估计,每个时间步都进行预测和更新,不断提高状态估计的精度。
总之,卡尔曼滤波的核心思想是在状态估计中同时考虑先验信息和测量信息,通过动态系统模型和测量模型的融合来估计系统的状态,并随着时间的推移不断改进估计的精度。这使得卡尔曼滤波器在处理具有不确定性和噪声的动态系统时非常有效。
核心公式
状态向量 (State Vector): 表示系统的状态,通常用 x 表示。状态向量可以是多维的,包括系统在不同方面的参数。在时刻 k,状态向量表示为 x(k)。
状态协方差矩阵 (State Covariance Matrix): 表示状态估计的不确定性,通常用 P 表示。它描述了每个状态参数的方差和协方差。在时刻 k,状态协方差矩阵表示为 P(k)。
系统动态方程 (State Transition Equation): 描述状态如何随时间变化,通常表示为状态转移矩阵 A 和控制输入向量 B(如果适用)。系统动态方程可以表示为以下公式:
x(k+1) = A * x(k) + B * u(k) + w(k)
其中,x(k) 表示时刻 k 的状态向量,u(k) 表示时刻 k 的控制输入向量(如果适用),w(k) 表示过程噪声。
观测矩阵 (Observation Matrix): 描述如何从测量中获得观测数据,通常表示为 H。观测矩阵将状态向量映射到观测数据的空间。观测方程可以表示为以下公式:
z(k) = H * x(k) + v(k)
其中,z(k) 表示时刻 k 的观测数据,v(k) 表示观测噪声。
观测噪声协方差矩阵 (Observation Noise Covariance Matrix): 描述观测数据的噪声性质,通常表示为 R。它表示观测数据中的方差和协方差。
这些公式构成了卡尔曼滤波的核心数学表述。滤波器的工作包括在每个时间步进行以下两个主要步骤:
**预测步骤 (**Prediction Step): 根据系统动态方程进行状态预测,同时更新状态协方差矩阵以反映预测的不确定性。
更新步骤 (Update Step): 利用观测数据来更新状态估计,根据观测矩阵和观测噪声协方差矩阵来计算新的状态估计和状态协方差矩阵。
卡尔曼滤波的目标是通过这两个步骤连续迭代,不断提高对系统状态的估计精度。这些数学公式和步骤构成了卡尔曼滤波算法的核心,用于处理具有不确定性和噪声的动态系统。
一维卡尔曼滤波器示例
本示例演示了一维卡尔曼滤波器的基本实现步骤。
导入所需的库
import numpy as np
import matplotlib.pyplot as plt
在此示例中,我们导入了NumPy用于数值计算和Matplotlib用于绘图。
定义卡尔曼滤波器参数
A = 1 # 状态转移矩阵
H = 1 # 观测矩阵
Q = 0.01 # 状态噪声的协方差
R = 0.1 # 观测噪声的协方差
x_hat = 0 # 初始状态估计
P = 1 # 初始估计误差的协方差
这些参数用于定义卡尔曼滤波器的模型。A是状态转移矩阵,H是观测矩阵,Q和R是状态噪声和观测噪声的协方差,x_hat是初始状态估计,P是初始估计误差的协方差。
生成模拟数据
true_values = np.linspace(0, 10, 100)
measurements = true_values + np.random.normal(0, np.sqrt(R), 100)
在此示例中,我们生成了一个包含100个数据点的"真实值"和带有观测噪声的测量值。
初始化滤波器
filtered_values = []
我们初始化一个空列表来存储卡尔曼滤波器估计的状态值。
迭代处理测量值
for z in measurements:
我们遍历测量值列表。
预测步骤
x_hat_minus = A * x_hat
P_minus = A * P * A + Q
在每个时间步骤中,我们执行预测步骤。首先,我们使用状态转移矩阵A估计下一个状态(x_hat_minus),然后更新估计误差的协方差(P_minus)。
更新步骤
K = P_minus * H / (H * P_minus * H + R)
x_hat = x_hat_minus + K * (z - H * x_hat_minus)
P = (1 - K * H) * P_minus
在更新步骤中,我们计算卡尔曼增益K,然后使用测量值来更新状态估计(x_hat)和估计误差的协方差(P)。
存储估计值
filtered_values.append(x_hat)
我们将每个时间步骤的估计状态值存储在filtered_values列表中。
绘制结果
plt.figure(figsize=(12, 6))
plt.plot(true_values, label='True Values', color='b')
plt.plot(measurements, label='Measurements', color='g', alpha=0.5)
plt.plot(filtered_values, label='Filtered Values', color='r')
plt.legend()
plt.title('Kalman Filter Demo')
plt.xlabel('Time Steps')
plt.ylabel('Value')
plt.show()
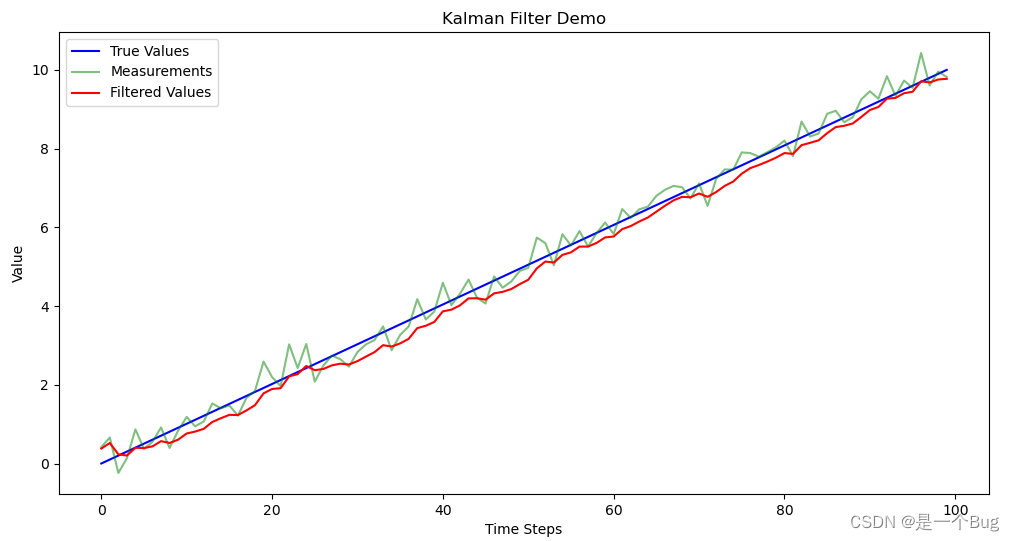
最后,我们使用Matplotlib绘制了"真实值"、测量值和卡尔曼滤波器估计的值的图表,以可视化卡尔曼滤波的效果。
这就是一维卡尔曼滤波器的基本实现步骤。卡尔曼滤波器的关键在于预测和更新步骤,其中卡尔曼增益(K)用于融合测量值和状态估计,从而提供更准确的状态估计。在实际应用中,卡尔曼滤波器可以用于传感器数据融合、目标跟踪等各种应用中。
相关文章:

卡尔曼滤波应用在数据处理方面的应用
卡尔曼滤波应用到交通领域 滤波器介绍核心思想核心公式一维卡尔曼滤波器示例导入所需的库 滤波器介绍 卡尔曼滤波器是一种用于估计系统状态的数学方法,它以卡尔曼核心思想为基础,广泛应用于估计动态系统的状态和滤除测量中的噪声。以下是卡尔曼滤波器的核…...

PROFIBUS主站转ETHERCAT协议网关
产品介绍 JM-DPM-ECT是自主研发的一款PROFIBUS-DP主站功能的通讯网关。该产品主要功能是将各种PROFIBUS-DP从站接入到ETHERCAT网络中。 本网关连接到PROFIBUS总线中作为主站使用,连接到ETHERCAT总线中作为从站使用。 产品参数 技术参数 ◆ PROFIBUS-DP/V0 协议符…...

Vue路由的使用及node.js下载安装和环境搭建
目录 一、Vue路由 1.1 简介 ( 1 ) 特点 ( 2 ) 作用 1.2 实例 ( 1 ) 引入 ( 2 ) 组件 ( 3 ) 关系 ( 4 ) 路由 ( 5 ) 事件 ( 6 ) 锚点 二、nodeJS 2.1 下载 2.2 安装 2.3 环境搭建 新增 添加 测试 配置 运行 一、Vue路由 1.1 简介 Vue路由是Vue.…...
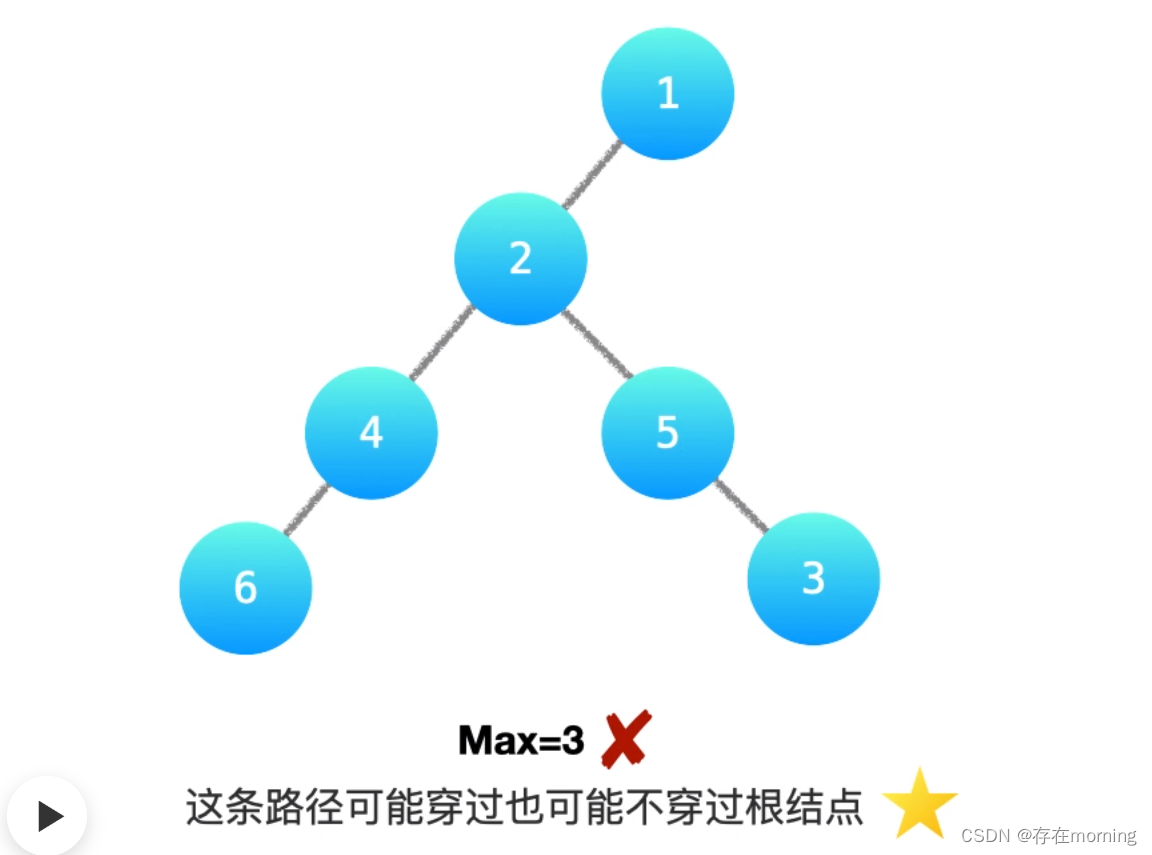
【算法训练-二叉树 三】【最大深度与直径】求二叉树的最大深度、求二叉树的直径
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【求二叉树的直径】,使用【二叉树】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件…...

查看linux是centos还是Ubuntu
查看linux是centos还是Ubuntu 命令:cat /etc/os-release...

win10怎么关闭自动更新,这个方法你知道吗?
Windows 10 操作系统自动更新是确保系统安全性和性能的关键功能。然而,有时用户可能希望手动控制更新,因此关闭自动更新可能是一个有用的选项。在本文中,我们将介绍win10怎么关闭自动更新的两种方法,以满足用户不同的需求。 方法1…...

「语音芯片」常见的OTP芯片故障分析
OTP语音芯片是指一次性可编程语音芯片,语音只能烧写一次,适合应用在不需要修改语音、语音长度短的场合,从放音的长度上可以分为20秒、40秒、80秒、170秒、340秒。语音芯片的特点是单芯片方案、价格便宜,适合批量生产,即便是小数量…...

孩子写作业买什么样台灯合适?适合孩子读写台灯推荐
现在孩子的普遍都存在视力问题,而导致孩子近视的原因可能跟光线太强或太弱、不用的用眼习惯、长时间的过度用眼等因素有关,根据数据表明目前中国近视患者人数达到6亿多,其中儿童青少年的视力不良率甚至高达八成,所以在孩子的学习道…...

DBAPI插件开发指南
DBAPI插件开发指南 插件市场 您可以去插件市场下载插件 插件的作用 DBAPI的插件分4类,分别是数据转换插件、缓存插件、告警插件、全局数据转化插件 缓存插件 对执行器结果进行缓存,比如SQL执行器,对查询类SQL,sql查询结果进…...

线程池使用之自定义线程池
目录 一:Java内置线程池原理剖析 二:ThreadPoolExecutor参数详解 三:线程池工作流程总结示意图 四:自定义线程池-参数设计分析 1:核心线程数(corePoolSize) 2:任务队列长度(workQueue) 3:最大线程数(maximumPoolSize) 4:最…...
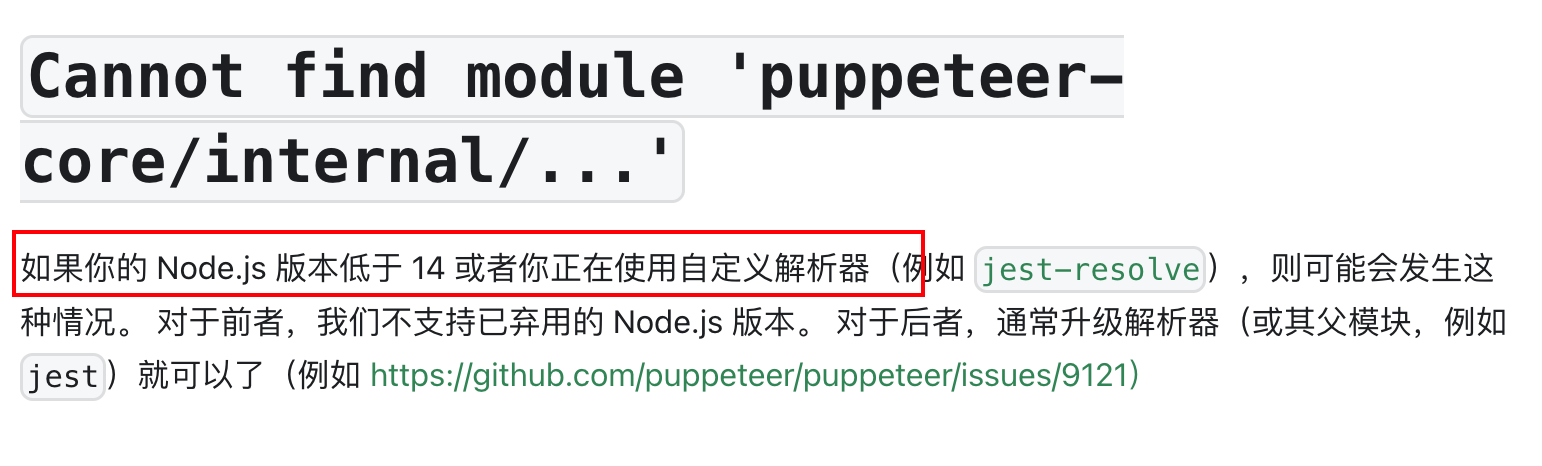
Puppeteer无头浏览器:开启自动化之门,掌握浏览器世界的无限可能
大概还是入门期,我曾用Puppeteer做爬虫工具以此来绕过某网站的防爬机制。近期有需求要做任意链接网页截图,像这种场景非常适合用Puppeteer完成。无头浏览器我已知的还有Selenium。 完成截图需求踩的最大的坑不是具体的逻辑代码,而是Docker部…...

Ubuntu 23.10/24.04 LTS 放弃默认使用 snap 版 CUPS 打印堆栈
导读Canonical 的开发者、OpenPrinting 的项目负责人 Till Kamppeter 今年 5 月表示,计划在 Ubuntu 23.10(Mantic Minotaur)上默认使用 Snap 版本的 CUPS 打印堆栈。 不过经过数月的测试,官方放弃了这项决定。Ubuntu 23.10&#x…...

Linux CentOS7 history命令
linux查看历史命令可以使用history命令,该命令可以列出所有已键入的命令。 这个命令的作用可以让用户或其他有权限人员,进行审计,查看已录入的命令。 用户所键入的命令作为应保存的信息将记录在文件中,这个文件就是家目录中的一…...
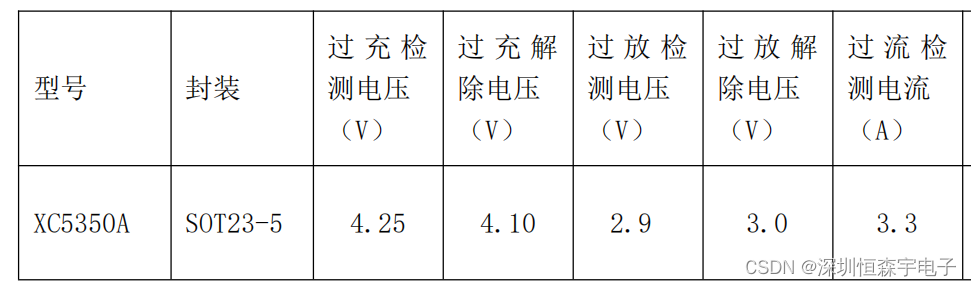
XC5350A 单节锂电池保护芯片 过放2.9V/2.8V/2.4V保护IC
XC5350A产品是一个高集成度的鲤离子/聚合物电池保护解决方案。XC5350A包含先进的功率MOSFET,高精度电压检测电路和延迟电路XC5350A放入一个超小型SOT23-5封装,只有一个外部元件使其成为在电池组有限的空间的理想解决方案。 XC5350A具有包括过充ÿ…...

单片机论文参考:1、基于单片机的电子琴
摘要 随着社会的发展进步,音乐逐渐成为我们生活中很重要的一部分,有人曾说喜欢音乐的人不会向恶。我们都会抽空欣赏世界名曲,作为对精神的洗礼。本论文设计一个基于单片机的简易电子琴。电子琴是现代电子科技与音乐结合的产物,是一…...
算法)
Opencv源码解析(2)算法
目录 一,直方图均衡 1,直方图统计 2,灰度变换 3,直方图均衡 二,可分离滤波器 1,可分离滤波器的工厂 2,ocvSepFilter、sepFilter2D 3,Sobel 三,相位相关法 phase…...
让Mac菜单栏变得更加美观整洁——Bartender 5
Bartender 5是一款Mac电脑上的菜单栏图标管理软件,能够帮助您把菜单栏上的图标整理得更加美观、整洁和易于使用。如果您的菜单栏上充斥着许多图标,导致视觉上很不舒适和疲劳,那么Bartender 5就是解决这一问题的最佳选择! Bartend…...

服务器迁移:无缝过渡指南
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

安卓开发中ViewBinding的使用
在安卓开发中,ViewBing 的作用就是简化 findViewById() 代码的写法。 看看下面的替换: etbinding.text //etfindViewById(R.id.text) 下面就看看怎么用的, 首先,打开app模块的build.gradle,然后添加如下代码&…...
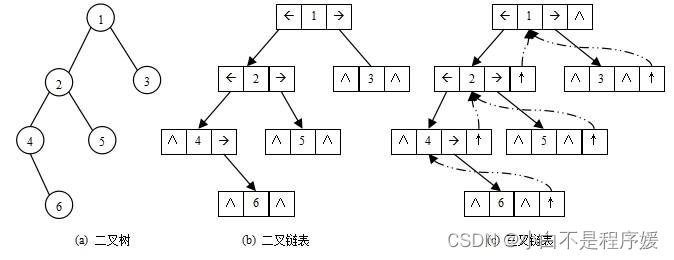
【初阶数据结构】树(tree)的基本概念——C语言
目录 一、树(tree) 1.1树的概念及结构 1.2树的相关概念 1.3树的表示 1.4树在实际中的运用(表示文件系统的目录树结构) 二、二叉树的概念及结构 2.1二叉树的概念 2.2现实中真正的二叉树 2.3特殊的二叉树 2.4二叉树的性质…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
