数据结构:树和二叉树之-堆排列 (万字详解)
目录
树概念及结构
1.1树的概念
1.2树的表示
编辑2.二叉树概念及结构
2.1概念
2.2数据结构中的二叉树:编辑
2.3特殊的二叉树:
编辑
2.4 二叉树的存储结构
2.4.1 顺序存储:
2.4.2 链式存储:
二叉树的实现及大小堆排列
1功能展示
2 定义基本结构
3 初始化
4打印
5销毁
6插入
7向上调整
8交换两数组元素之间的值
9删除
10向下调整
11取堆顶的元素
12 判断二叉树是否为空
13计算该二叉树元素个数
3,堆排列
1建堆
建堆方式1 时间复杂度:O(N*log(N))
建堆方式2 时间复杂度:O(N)
2排列数组 O(N * log(N))
成品展示
Head.h
Head.c
Test.c
树概念及结构
1.1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它
叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
有一个特殊的结点,称为根结点,根节点没有前驱结点
除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集
合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以
有0个或多个后继
因此,树是递归定义的。

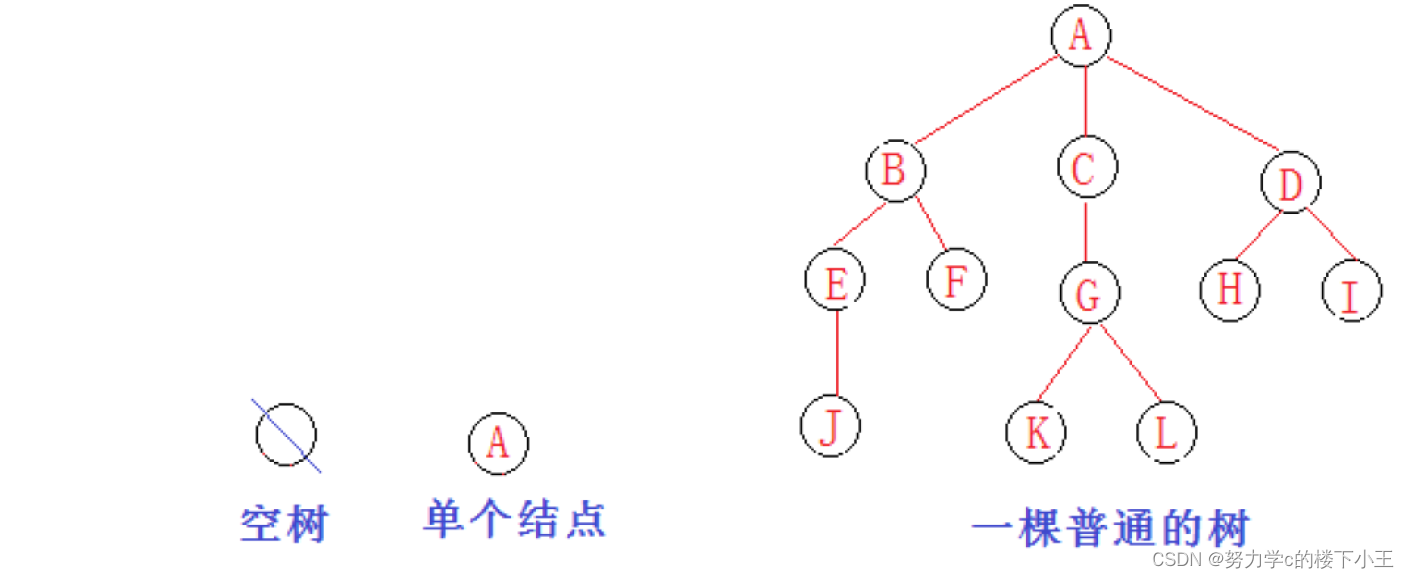

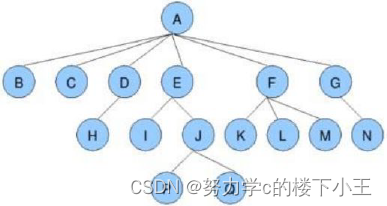
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
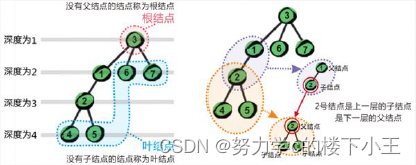
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的多颗树的集合称为森林;(数据结构中的学习并查集本质就是一个森林)
1.2树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,
如:双亲表示法,孩子表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子
兄弟表示法。
typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _pNextBrother; // 指向其下一个兄弟结点
DataType _data; // 结点中的数据域
};
 2.二叉树概念及结构
2.二叉树概念及结构
2.1概念
一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子
树和右子树的二叉树组成。
二叉树的特点:
- 每个结点最多有两棵子树,即二叉树不存在度大于2的结点。
- 二叉树的子树有左右之分,其子树的次序不能颠倒。
2.2数据结构中的二叉树:
2.3特殊的二叉树:
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉
树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。 - 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对
于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号
从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉
树
2.4 二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
二叉树的性质
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h- 1.
- 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0=n2
+1 - 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=LogN
2.4.1 顺序存储:
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树
会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲
解。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
2.4.2 链式存储:
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面课程学到高阶数据结构如红黑树等会用到三叉链。
二叉树的实现及大小堆排列
本文将以写代码思路进行讲述,故中间会出现代码的优化以便梳理思路,渐入佳境
本文分成三个文件:
Head.h//函数的声明
Head.c//函数的创建
Test.c //用于测试文件
1功能展示
//用数组的方式来表示二叉树基本结构typedef int HPDataType;typedef struct Heap{HPDataType* a;int size;int capacity;}HP;//初始化void HeapInit(HP* php);//交换两数组元素之间的值void Swap(HPDataType* p1,HPDataType* p2);//打印void HeapPrint(HP* php);//销毁void HeapDestroy(HP* php);//插入void HeapPush(HP* php,HPDataType x);//向下调整void AdjustDown(HPDataType* a, int size, int paarent);//向下调整void AdjustUp(HPDataType x, int child);//删除void HeapPop(HP* php);//取堆顶的元素HPDataType HeapTop(HP* php);//判断是否为空bool HeapEmpty(HP* php);//计算该二叉树元素个数int HeapSize(HP* php);
2 定义基本结构
使用数组实现二叉树相较于链表有以下优势:
1. 内存连续性:数组在内存中是连续存储的,而链表中的节点可以分布在内存的任意位置。在某些场景下,数组的内存连续性可以提高访问效率,尤其对于计算机的缓存机制来说,连续的数组元素可以更好地利用缓存行,减少缓存缺失。
2. 索引访问:数组可以通过索引直接访问元素,而链表需要从头节点开始顺序遍历才能找到指定位置的节点。通过索引可以快速访问数组中的元素,这在一些特定的操作中是非常有优势的,例如查找某个特定位置的节点、根据节点索引快速更新或删除元素等。
3. 空间效率:相比链表,数组实现二叉树可以更加节省空间。链表除了存储节点本身的数据之外,还需要额外的指针来连接节点,而数组只需要存储节点数据,不需要额外的指针。
需要注意的是,链表在插入和删除节点的操作上通常比数组更加高效,因为插入和删除只需要改变相邻节点之间的指针指向,而数组需要移动元素。因此,在对二叉树进行频繁的插入和删除操作时,链表可能更适合。而数组适合于对二叉树进行频繁的随机访问和操作的场景。
//用数组的方式来表示二叉树基本结构
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;
3 初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}
4打印
void HeapPrint(HP* php)
{assert(php);for (int i = 0;i < php->size;i++){printf("%d ", php->a[i]);}printf("\n");
}
5销毁
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a=NULL;php->size = php->capacity = 0;
}6插入
void HeapPush(HP* php, HPDataType x)
{assert(php);//扩容if (php->size == php->capacity){//判断capacity是否为0,并进行赋值int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = realloc(php->a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){printf("realloc fail\n");exit(-1);}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;// 当前数组 插入数值的位置AdjustUp(php->a, php->size-1);
}
7向上调整
在插入元素之时,直接进行向上排序
将插入的元素与父辈元素进行比较,并进行互换
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;//孩子被调到顶是结束(即数组首元素)while (child>0){//if (a[child]<a[parent]) 小堆if (a[child] > a[parent])//大堆{//孩子 小于/小于 父亲Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{//孩子 大于/小于 父亲break;}}
}8交换两数组元素之间的值
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
9删除
将头部元素与尾部元素呼唤,以防直接删除头元素,倒是数据混乱
将其换到尾部进行删除,在将换到同部的尾元素进行向下比较,
进行替换,寻找新的(最大/最小)头部元素
void HeapPop(HP* php)
{assert(php);assert(php->size>0);Swap(&(php->a[0]), &(php->a[php->size - 1]));php->size--;//向下调整AdjustDown(php->a, php->size, 0);
}
10向下调整
void AdjustDown(HPDataType* a, int size, int parent)
{int child = parent * 2 + 1;while (child<size){//选出左右孩子中 小/大 的那个//if (child+1<size && a[child + 1] < a[child])if (child + 1 < size && a[child + 1] > a[child]){++child;}//跟孩子父亲比较//if (a[child]<a[parent])if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{//左右孩子都大于/小于父亲,结束交换break;}}
}
11取堆顶的元素
//取堆顶的元素
HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}
12 判断二叉树是否为空
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}
13计算该二叉树元素个数
int HeapSize(HP* php)
{assert(php);return php->size ;
}
3,堆排列
此时二叉树已近成型,但进行排列时会设计到复杂度的问题,之前的代码中存在问题,效率低下
此时的问题:
1,你得先写一个Hp数据结构,反而复杂
2,有o(N)空间复杂度
每次使用建堆选数据
整体时间复杂度O(N^2)
效率太低,没有使用到堆的优势
每次使用堆排列时都要重新创建一个数据结构,并依次插入进行排序无疑是增加了时间复杂度
应该直接利用本身的数组进行堆排列
1建堆
建堆方式1 时间复杂度:O(N*log(N))
一共N个数,每个数向上调整log(N)次(层数,依次对父辈进行交换)
故为 O(Nlog(N))
for (int i = 1; i < n; i++){//每插入一个,进行一次向上调整AdjustUp(a, i);}
这段代码使用了一个循环,其中执行了n-1次迭代(从i=1到i<n)。每次循环内部都会调用
AdjustUp(a, i)进行向上调整的操作。
在循环内部,执行向上调整的操作的时间复杂度是O(log(i)),其中i是当前循环的迭代次数。因为每次执行向上调整时,需要比较和交换的次数与当前节点所在二叉树的高度有关,而二叉树的高度是随着节点的插入逐渐增加的,即高度与插入的节点数量有关。
根据每次迭代的时间复杂度为O(log(i)),加上n-1次的循环,总的时间复杂度为: O(log(1) + log(2) + … + log(n-1))
对于这个求和过程,并没有一个简单的封闭解析解。但根据级数求和的性质,可以得到这个求和结果的上界为O(n * log(n))。因此,可以将上述代码的时间复杂度近似地表示为O(n * log(n))。
需要注意,这个时间复杂度是在假设AdjustUp的时间复杂度为O(log(i))的情况下得到的。如果AdjustUp的时间复杂度比O(log(i))更高,那么整个代码块的时间复杂度将会增加。
建堆方式2 时间复杂度:O(N)
从最后一个非叶节点进行插入
for (int i = (n - 1) / 2; i >= 0; i--){//最后一个非叶节点:(n - 1) / 2//向下调整前提是字树必须是大/小堆AdjustDown(a, n, i);}
这段代码使用了一个循环,其中执行了(n-1)/2+1次迭代,从i=(n-1)/2到i=0。
每次循环内部都会调用AdjustDown(a, n, i)进行向下调整的操作。
在循环内部,执行向下调整的操作的时间复杂度是O(log(n)),其中n是当前二叉树的节点数量。因为每次执行向下调整时,需要比较和交换的次数与当前节点所在的子树的节点数量有关,而每个节点至多有两个子节点,所以向下调整的时间复杂度是与当前节点所在的子树高度相关,即O(log(n))。
根据每次迭代的时间复杂度为O(log(n)),加上(n-1)/2+1次的循环,总的时间复杂度为: O(log(n) + log(n) + … + log(n))
展开求和后,得到 (n-1)/2+1 次 log(n) 相加。根据级数求和的性质,这个求和结果为 O(n)。因此,可以将上述代码的时间复杂度近似地表示为 O(n)。
2排列数组 O(N * log(N))
此时二叉树已经排列完成,在二叉树图像中元素已经按照 大堆/小堆 排好
但在数组中依旧是混乱排列,要做到像堆排列,就需要将数组进行排列
升序打印数组:大堆
降序打印数组:小堆
这里似乎与之前相反
之前:
升序/降序 打印是要将首元素置换到末元素,并进行打印删除,被置换的元素向下调整
故为升序打印为小堆,降序为大堆
而此处我们要将数组按照大小堆的形式排列:
while (end>0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;//--end缩小范围保证是按照数组 大/小 堆排序}


若原本二叉树排列为大堆,该代码就将数组排列成大堆
故 升序建大堆,降序建小堆
成品展示
Head.h
#pragma once
#include <stdlib.h>
#include <stdio.h>
#include <assert.h>
#include <stdbool.h>//用数组的方式来表示二叉树基本结构
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;//初始化
void HeapInit(HP* php);//交换两数组元素之间的值
void Swap(HPDataType* p1, HPDataType* p2);//打印
void HeapPrint(HP* php);//销毁
void HeapDestroy(HP* php);//插入
void HeapPush(HP* php, HPDataType x);//向上调整
void AdjustUp(HPDataType x, int child);//向下调整
void AdjustDown(HPDataType* a, int size, int paarent);//删除
void HeapPop(HP* php);//取堆顶的元素
HPDataType HeapTop(HP* php);//判断是否为空
bool HeapEmpty(HP* php);//计算该二叉树元素个数
int HeapSize(HP* php);
Head.c
#include "Head.h"//初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}//打印
void HeapPrint(HP* php)
{assert(php);for (int i = 0;i < php->size;i++){printf("%d ", php->a[i]);}printf("\n");
}//销毁
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}//交换两数组元素之间的值
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}//向上调整
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;//孩子被调到顶是结束(即数组首元素)while (child > 0){if (a[child]<a[parent]) //小堆{//孩子 小于/小于 父亲Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{//孩子 大于/小于 父亲break;}}
}//插入
void HeapPush(HP* php, HPDataType x)
{assert(php);//扩容if (php->size == php->capacity){//判断capacity是否为0,并进行赋值int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = realloc(php->a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){printf("realloc fail\n");exit(-1);}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;// 当前数组 插入数值的位置AdjustUp(php->a, php->size - 1);}//向下调整
void AdjustDown(HPDataType* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){//选出左右孩子中 小/大 的那个if (child+1<size && a[child + 1] < a[child]){++child;}//跟孩子父亲比较if (a[child]<a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{//左右孩子都大于/小于父亲,结束交换break;}}
}//删除
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&(php->a[0]), &(php->a[php->size - 1]));php->size--;//向下调整AdjustDown(php->a, php->size, 0);
}//取堆顶的元素
HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}//判断是否为空
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}//计算该二叉树元素个数
int HeapSize(HP* php)
{assert(php);return php->size;
}
Test.c
Test.c只是用于测试代码,菜单的写法本文将不进行讲解。
但Test.c中含有对查找and销毁and存储链元素个数的使用方法进行了示例可以当参考。
#include "Head.h"void test1()
{//升序打印--小堆//降序打印--大堆HP hp;HeapInit(&hp);int a[] = { 27,15,19,18,28,34,65,49,25,37 };int sz = sizeof(a) / sizeof(a[0]);//将数组插入新的堆for (int i = 0;i < sz;i++){HeapPush(&hp, a[i]);}while (!HeapEmpty(&hp)){printf("%d ", HeapTop(&hp));HeapPop(&hp);}
}void test2()
{HP hp;HeapInit(&hp);int a[] = { 27,15,19,18,28,34,65,49,25,37 };int sz = sizeof(a) / sizeof(a[0]);//将数组插入新的堆for (int i = 0;i < sz;i++){HeapPush(&hp, a[i]);}int i = 0;while (!HeapEmpty(&hp)){a[i++] = HeapTop(&hp);HeapPop(&hp);}HeapDestroy(&hp);
}void test3()
{HP hp;HeapInit(&hp);int a[] = { 27,15,19,18,28,34,65,49,25,37 };int sz = sizeof(a) / sizeof(a[0]);//将数组插入新的堆for (int i = 0;i < sz;i++){HeapPush(&hp, a[i]);}HeapPrint(&hp);
}
//此时的问题:
//1,你得先写一个Hp数据结构,反而复杂
//2,有o(N)空间复杂度
/*每次使用建堆选数据整体时间复杂度O(N^2)效率太低,没有使用到堆的优势
*/
void test4(int*a ,int n)
{//本生就是一个数组,直接利用自身建堆//建堆// 建堆方式1 时间复杂度:O(N*log(N))//for (int i = 1; i < n; i++)//{// //每插入一个,进行一次向上调整// AdjustUp(a, i);//}// 建堆方式2 时间复杂度:O(N)for (int i = (n - 1) / 2; i >= 0; i--){//最后一个非叶节点:(n - 1) / 2//向下调整前提是字树必须是大/小堆AdjustDown(a, n, i);}}/*1.将 最大的数/最小的数 换到 最小的数/最大的数,并删除被换的数(最后的数)2.然后对 头部进行降序(将 最小的数/最大的数 下移,重新找到 最大/最小 的数换到头部) 将效率提升至O(N*log(N))
*/
//升序 --建大堆
//降序 --建小堆
void test5(int* a, int n)
{//时间复杂度:O(N)for (int i = (n - 1) / 2; i >= 0; i--){//最后一个非叶节点:(n - 1) / 2//向下调整前提是字树必须是大/小堆AdjustDown(a, n, i);}int end = n - 1;//O(N * log(N))->O(N)+O(N * log(N))=O(N * log(N))while (end>0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}int main()
{int a[] = { 5, 3, 2, 9, 7, 4, 1, 10, 8, 6};int sz = sizeof(a) / sizeof(a[0]);test5(a,sz);return 0;
}
本文到这就结束啦,本文为万字解读,创作不易,若喜欢请留下免费的赞吧!
感谢阅读😊😊😊

相关文章:

数据结构:树和二叉树之-堆排列 (万字详解)
目录 树概念及结构 1.1树的概念 1.2树的表示 编辑2.二叉树概念及结构 2.1概念 2.2数据结构中的二叉树:编辑 2.3特殊的二叉树: 编辑 2.4 二叉树的存储结构 2.4.1 顺序存储: 2.4.2 链式存储: 二叉树的实现及大小堆…...

爬虫入门基础:深入解析HTTP协议的工作过程
目录 一、HTTP协议简介 二、HTTP协议的工作过程 三、请求方法与常见用途 四、请求头与常见字段 五、状态码与常见含义 六、进阶话题和注意事项 总结 在如今这个数字化时代,互联网已经成为我们获取信息、交流和娱乐的主要渠道。而在互联网中,HTTP协…...
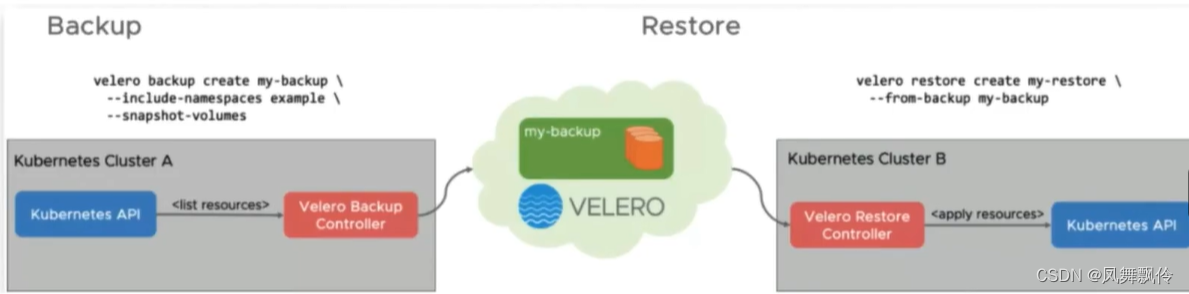
k8备份与恢复-Velero
简介 Velero 是一款可以安全的备份、恢复和迁移 Kubernetes 集群资源和持久卷等资源的备份恢复软件。 Velero 实现的 kubernetes 资源备份能力,可以轻松实现 Kubernetes 集群的数据备份和恢复、复制 kubernetes 集群资源到其他kubernetes 集群或者快速复制生产环境…...

基于Python开发的火车票分析助手(源码+可执行程序+程序配置说明书+程序使用说明书)
一、项目简介 本项目是一套基于Python开发的火车票分析助手,主要针对计算机相关专业的正在做毕设的学生与需要项目实战练习的Python学习者。 包含:项目源码、项目文档等,该项目附带全部源码可作为毕设使用。 项目都经过严格调试,…...

旺店通·企业奇门与金蝶云星空对接集成订单查询连通销售订单新增(旺店通销售-金蝶销售订单-小红书)
旺店通企业奇门与金蝶云星空对接集成订单查询连通销售订单新增(旺店通销售-金蝶销售订单-小红书) 接通系统:旺店通企业奇门 慧策最先以旺店通ERP切入商家核心管理痛点——订单管理,之后围绕电商经营管理中的核心管理诉求,先后布局流量获取、会…...
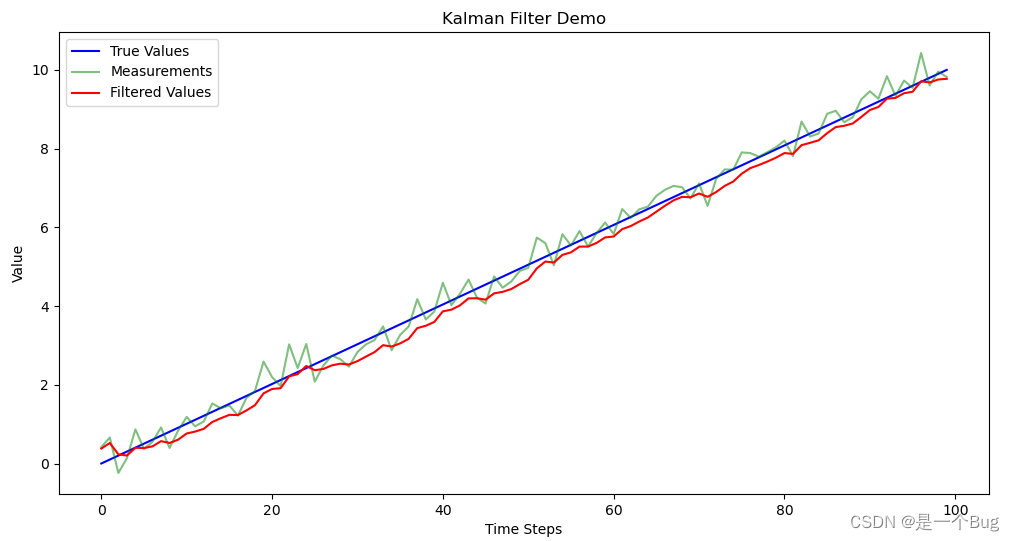
卡尔曼滤波应用在数据处理方面的应用
卡尔曼滤波应用到交通领域 滤波器介绍核心思想核心公式一维卡尔曼滤波器示例导入所需的库 滤波器介绍 卡尔曼滤波器是一种用于估计系统状态的数学方法,它以卡尔曼核心思想为基础,广泛应用于估计动态系统的状态和滤除测量中的噪声。以下是卡尔曼滤波器的核…...

PROFIBUS主站转ETHERCAT协议网关
产品介绍 JM-DPM-ECT是自主研发的一款PROFIBUS-DP主站功能的通讯网关。该产品主要功能是将各种PROFIBUS-DP从站接入到ETHERCAT网络中。 本网关连接到PROFIBUS总线中作为主站使用,连接到ETHERCAT总线中作为从站使用。 产品参数 技术参数 ◆ PROFIBUS-DP/V0 协议符…...

Vue路由的使用及node.js下载安装和环境搭建
目录 一、Vue路由 1.1 简介 ( 1 ) 特点 ( 2 ) 作用 1.2 实例 ( 1 ) 引入 ( 2 ) 组件 ( 3 ) 关系 ( 4 ) 路由 ( 5 ) 事件 ( 6 ) 锚点 二、nodeJS 2.1 下载 2.2 安装 2.3 环境搭建 新增 添加 测试 配置 运行 一、Vue路由 1.1 简介 Vue路由是Vue.…...
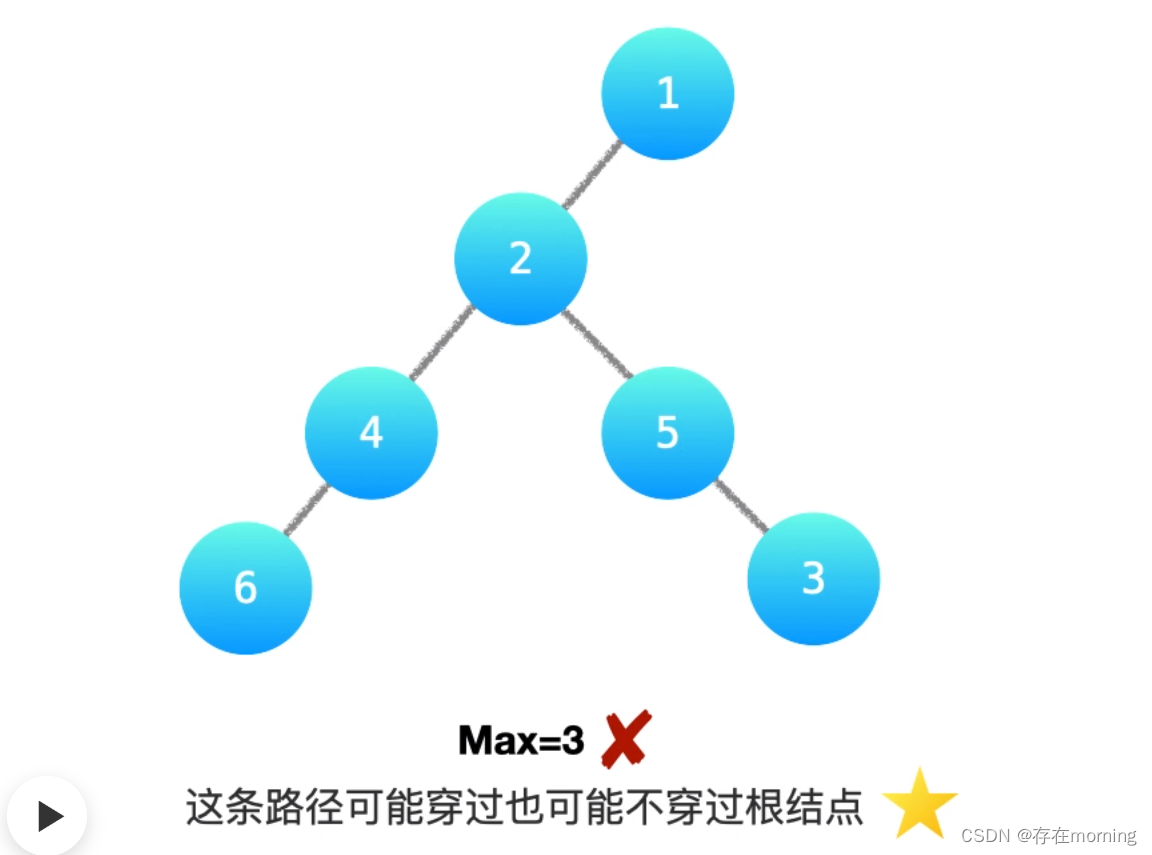
【算法训练-二叉树 三】【最大深度与直径】求二叉树的最大深度、求二叉树的直径
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【求二叉树的直径】,使用【二叉树】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件…...

查看linux是centos还是Ubuntu
查看linux是centos还是Ubuntu 命令:cat /etc/os-release...

win10怎么关闭自动更新,这个方法你知道吗?
Windows 10 操作系统自动更新是确保系统安全性和性能的关键功能。然而,有时用户可能希望手动控制更新,因此关闭自动更新可能是一个有用的选项。在本文中,我们将介绍win10怎么关闭自动更新的两种方法,以满足用户不同的需求。 方法1…...

「语音芯片」常见的OTP芯片故障分析
OTP语音芯片是指一次性可编程语音芯片,语音只能烧写一次,适合应用在不需要修改语音、语音长度短的场合,从放音的长度上可以分为20秒、40秒、80秒、170秒、340秒。语音芯片的特点是单芯片方案、价格便宜,适合批量生产,即便是小数量…...

孩子写作业买什么样台灯合适?适合孩子读写台灯推荐
现在孩子的普遍都存在视力问题,而导致孩子近视的原因可能跟光线太强或太弱、不用的用眼习惯、长时间的过度用眼等因素有关,根据数据表明目前中国近视患者人数达到6亿多,其中儿童青少年的视力不良率甚至高达八成,所以在孩子的学习道…...

DBAPI插件开发指南
DBAPI插件开发指南 插件市场 您可以去插件市场下载插件 插件的作用 DBAPI的插件分4类,分别是数据转换插件、缓存插件、告警插件、全局数据转化插件 缓存插件 对执行器结果进行缓存,比如SQL执行器,对查询类SQL,sql查询结果进…...

线程池使用之自定义线程池
目录 一:Java内置线程池原理剖析 二:ThreadPoolExecutor参数详解 三:线程池工作流程总结示意图 四:自定义线程池-参数设计分析 1:核心线程数(corePoolSize) 2:任务队列长度(workQueue) 3:最大线程数(maximumPoolSize) 4:最…...
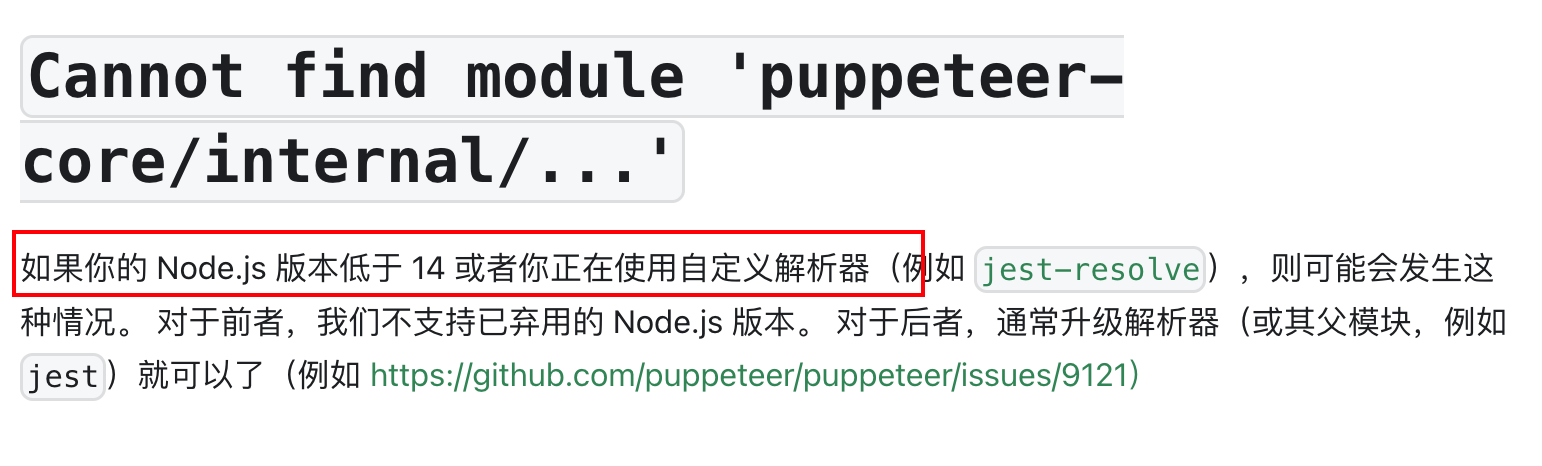
Puppeteer无头浏览器:开启自动化之门,掌握浏览器世界的无限可能
大概还是入门期,我曾用Puppeteer做爬虫工具以此来绕过某网站的防爬机制。近期有需求要做任意链接网页截图,像这种场景非常适合用Puppeteer完成。无头浏览器我已知的还有Selenium。 完成截图需求踩的最大的坑不是具体的逻辑代码,而是Docker部…...

Ubuntu 23.10/24.04 LTS 放弃默认使用 snap 版 CUPS 打印堆栈
导读Canonical 的开发者、OpenPrinting 的项目负责人 Till Kamppeter 今年 5 月表示,计划在 Ubuntu 23.10(Mantic Minotaur)上默认使用 Snap 版本的 CUPS 打印堆栈。 不过经过数月的测试,官方放弃了这项决定。Ubuntu 23.10&#x…...

Linux CentOS7 history命令
linux查看历史命令可以使用history命令,该命令可以列出所有已键入的命令。 这个命令的作用可以让用户或其他有权限人员,进行审计,查看已录入的命令。 用户所键入的命令作为应保存的信息将记录在文件中,这个文件就是家目录中的一…...
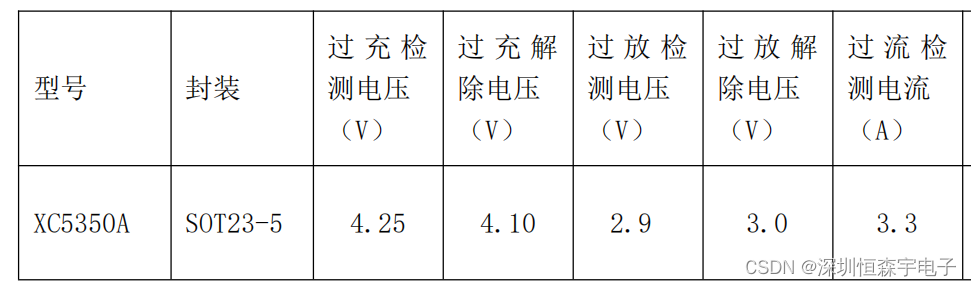
XC5350A 单节锂电池保护芯片 过放2.9V/2.8V/2.4V保护IC
XC5350A产品是一个高集成度的鲤离子/聚合物电池保护解决方案。XC5350A包含先进的功率MOSFET,高精度电压检测电路和延迟电路XC5350A放入一个超小型SOT23-5封装,只有一个外部元件使其成为在电池组有限的空间的理想解决方案。 XC5350A具有包括过充ÿ…...

单片机论文参考:1、基于单片机的电子琴
摘要 随着社会的发展进步,音乐逐渐成为我们生活中很重要的一部分,有人曾说喜欢音乐的人不会向恶。我们都会抽空欣赏世界名曲,作为对精神的洗礼。本论文设计一个基于单片机的简易电子琴。电子琴是现代电子科技与音乐结合的产物,是一…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

