二、链表(linked-list)
文章目录
- 一、定义
- 二、经典例题
- (一)[21.合并两个有序链表](https://leetcode.cn/problems/merge-two-sorted-lists/description/)
- 1.思路
- 2.复杂度分析
- 3.注意
- 4.代码
- (二)[86.分割链表](https://leetcode.cn/problems/partition-list/description/)
- 1.思路
- 2.复杂度分析
- 3.代码
- (三)[23.合并 K 个升序链表](https://leetcode.cn/problems/merge-k-sorted-lists/description/)
- 1.思路
- 2.复杂度分析
- 3.代码
- (四)[19.删除链表中的倒数第N个节点](https://leetcode.cn/problems/remove-nth-node-from-end-of-list/)
- 1.思路
- 2.复杂度分析
- 3.代码
一、定义
链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。 相比于线性表顺序结构,操作复杂。由于不必须按顺序存储,链表在插入的时候可以达到O(1)的复杂度,比另一种线性表顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要O(n)的时间,而线性表和顺序表相应的时间复杂度分别是O(logn)和O(1)。
二、经典例题
(一)21.合并两个有序链表
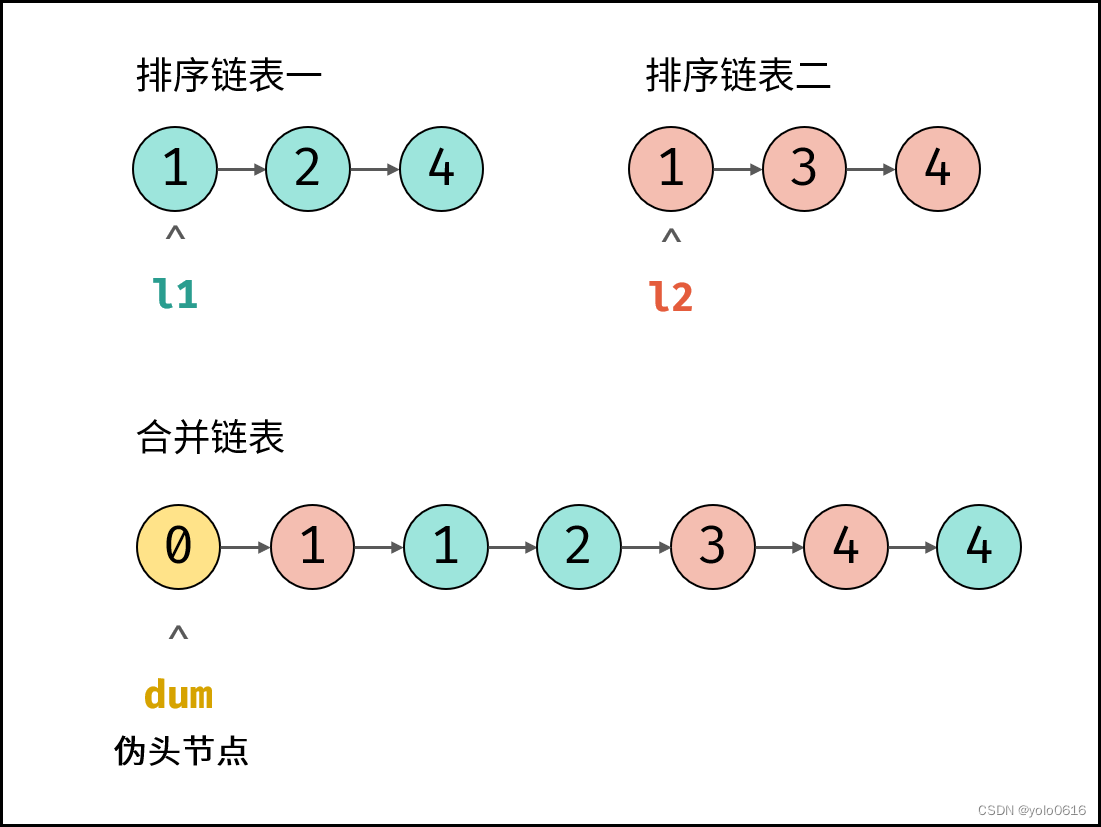
1.思路
根据题目描述,链表l1, l2是递增的,因此容易想到使用双指针cur1和cur2遍历两链表,根据cur1.val和cur2.val的大小关系确定节点添加顺序,两节点指针交替前进,直至遍历完毕。
同时因为两个链表都是有序的,所以,当我们遍历完一个链表,剩下的那个链表如果没到结尾,可以直接跟上。
2.复杂度分析
时间复杂度 O(M+N) : M,N别为两个链表的长度,合并操作需遍历两链表。
空间复杂度 O(1): 节点引用 dum , cur使用常数大小的额外空间。
3.注意
Dummy节点的作用是作为一个虚拟的头前节点。在不知道要返回的新链表的头结点是哪一个,它可能是原链表的第一个节点,可能在原链表的中间,也可能在最后,甚至不存在(nil)。引入Dummy节点可以涵盖所有情况,并且可以使用dummy.next返回最终需要的头结点。
4.代码
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {ListNode* cur1 = list1;ListNode* cur2 = list2;ListNode* dummy = new ListNode(-1); // 虚拟头结点ListNode* cur = dummy;while (cur1 && cur2) {// 比较 p1 和 p2 两个指针// 将值较小的的节点接到 p 指针if (cur1 -> val > cur2 -> val) {cur -> next = cur2;cur2 = cur2 -> next;}else {cur -> next = cur1;cur1 = cur1 -> next;}cur = cur -> next; // p 指针不断前进}if (cur1) cur -> next = cur1;if (cur2) cur -> next = cur2;return dummy -> next;}
};
(二)86.分割链表
1.思路
具体来说,我们可以把原链表分成两个小链表,一个链表中的元素大小都小于 x,另一个链表中的元素都大于等于 x,最后再把这两条链表接到一起,就得到了题目想要的结果。
2.复杂度分析
时间复杂度 O(N): 其中 N为链表长度;遍历链表使用线性时间。
空间复杂度 O(1) : 假头节点使用常数大小的额外空间。
3.代码
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* partition(ListNode* head, int x) {ListNode* dummy1 = new ListNode(-1);ListNode* dummy2 = new ListNode(-1);ListNode* small = dummy1;ListNode* big = dummy2;// 新建两个链表 small,big,分别用于添加所有节点值<x、节点值>=的节点ListNode* cur = head;while (cur) {if (cur -> val >= x) {big -> next = cur;big = big -> next;}else {small -> next = cur;small = small -> next;}cur = cur -> next;}small -> next = dummy2 -> next; // 拼接 small 和 bigbig -> next = nullptr;return dummy1 -> next;}
};
(三)23.合并 K 个升序链表
1.思路
如何快速得到 k 个节点中的最小节点,接到结果链表上?
- 这里我们就要用到 优先级队列(二叉堆) 这种数据结构,把链表节点放入一个最小堆,就可以每次获得 k 个节点中的最小节点:
优先队列 pq 中的元素个数最多是 k,所以一次 poll 或者 add 方法的时间复杂度是 O(logk);所有的链表节点都会被加入和弹出 pq,所以算法整体的时间复杂度是 O(Nlogk),其中 k 是链表的条数,N 是这些链表的节点总数。
2.复杂度分析
时间复杂度:考虑优先队列中的元素不超过 k 个,那么插入和删除的时间代价为 O(logk),这里最多有 kn 个点,对于每个点都被插入删除各一次,故总的时间代价即渐进时间复杂度为 O(kn×logk)。
空间复杂度:这里用了优先队列,优先队列中的元素不超过 k个,故渐进空间复杂度为 O(k)。
3.代码
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:
// 时间复杂度 : O(n ∗ log(k))ListNode* mergeKLists(vector<ListNode*>& lists) {if (lists.size() == 0) return nullptr;ListNode* dummy = new ListNode(-1);ListNode* p = dummy;priority_queue<ListNode*, vector<ListNode*>, function<bool(ListNode*, ListNode*)>> pq([] (ListNode* a, ListNode* b) { return a->val > b->val; });for (auto head : lists) {if (head != nullptr) pq.push(head);}while (!pq.empty()) {ListNode* node = pq.top();pq.pop();p -> next = node;if (node -> next != nullptr)pq.push(node->next);p = p -> next;}return dummy -> next;}
};
(四)19.删除链表中的倒数第N个节点
1.思路
假设链表有 n 个节点,倒数第 k 个节点就是正数第 n - k + 1 个节点。
是的,但是算法题一般只给你一个 ListNode 头结点代表一条单链表,你不能直接得出这条链表的长度 n,而需要先遍历一遍链表算出 n 的值,然后再遍历链表计算第 n - k + 1 个节点。
也就是说,这个解法需要遍历两次链表才能得到出倒数第 k 个节点。
2.复杂度分析
3.代码
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* removeNthFromEnd(ListNode* head, int n) {if (head == nullptr || n == 0) return nullptr;ListNode* dummy = new ListNode(-1);dummy -> next = head;ListNode* x = findFromEnd(dummy, n + 1);x -> next = x -> next -> next;return dummy -> next;}ListNode* findFromEnd(ListNode* head, int k) {// 代码见上文ListNode* slow = head;ListNode* fast = head;while (k -- && fast) {fast = fast -> next;}while (fast) {slow = slow -> next;fast = fast -> next;}return slow;}
};
相关文章:

二、链表(linked-list)
文章目录 一、定义二、经典例题(一)[21.合并两个有序链表](https://leetcode.cn/problems/merge-two-sorted-lists/description/)1.思路2.复杂度分析3.注意4.代码 (二)[86.分割链表](https://leetcode.cn/problems/partition-list…...
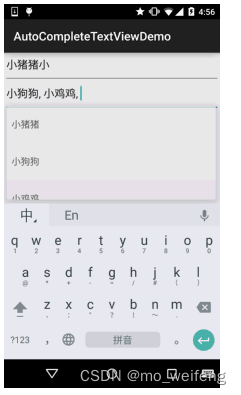
Android EditText筛选+选择功能开发
在日常开发中经常会遇到这种需求,EditText既需要可以筛选,又可以点击选择。这里筛选功能用的是AutoCompleteTextView,选择功能使用的是第三方库https://github.com/kongzue/DialogX。 Android AutoCompleteTextView(自动完成文本框)的基本使用…...

Linux 信号 alarm函数 setitimer函数
/*#include <unistd.h>unsigned int alarm(unsigned int seconds);功能:设置定时器。函数调用,开始倒计时,0的时候给当前的进程发送SIGALARM信号参数:倒计时的时长。。单位:秒 如果参数为0,无效返回…...

自主设计,模拟实现 RabbitMQ - 实现发送方消息确认机制
目录 一、实现发送方消息确认 1.1、需求分析 什么是发送方的消息确认? 如何实现?...

【数据结构】二叉树的·深度优先遍历(前中后序遍历)and·广度优先(层序遍历)
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...
优彩云采集器下载-免费优彩云采集器下载地址
免费优彩云采集器。您是否曾为了数据采集而感到头疼不已?是否一直在寻找一种能够轻松、高效地获取所需数据的方法?别着急,让我们一起来了解如何通过优彩云采集器解决这些问题,从而让您产生购买的欲望。 免费全自动采集发布批量管理…...

【Python】OJ 常用函数
这里写目录标题 一. math1. 求阶乘 - factorial()2. 绝对值 - fabs() 二. 容器的方法1. reverse() 三. Python 内置函数1. sort() 一. math 需要引入 math 包:import math 1. 求阶乘 - factorial() import math print(math.factorial(5))--------运行结果-------…...

【Vue】上万个字把事件处理讲解的淋漓尽致
hello,我是小索奇,精心制作的Vue系列教程持续更新哈,想要学习&巩固&避坑就一起学习吧~ 事件处理 事件的基本用法 重点内容 使用v-on:xxx缩写xxx绑定事件,其中 xxx 是事件名(回顾:v-bind缩写为冒号…...

Remmina中VNC、SSH和RDP的区别
Remmina 可以在 Linux 系统上对远程进行连接。它支持多种远程连接协议,包括 VNC(Virtual Network Computing)、SSH(Secure Shell)和 RDP(Remote Desktop Protocol)。这些协议用于实现不同类型的…...
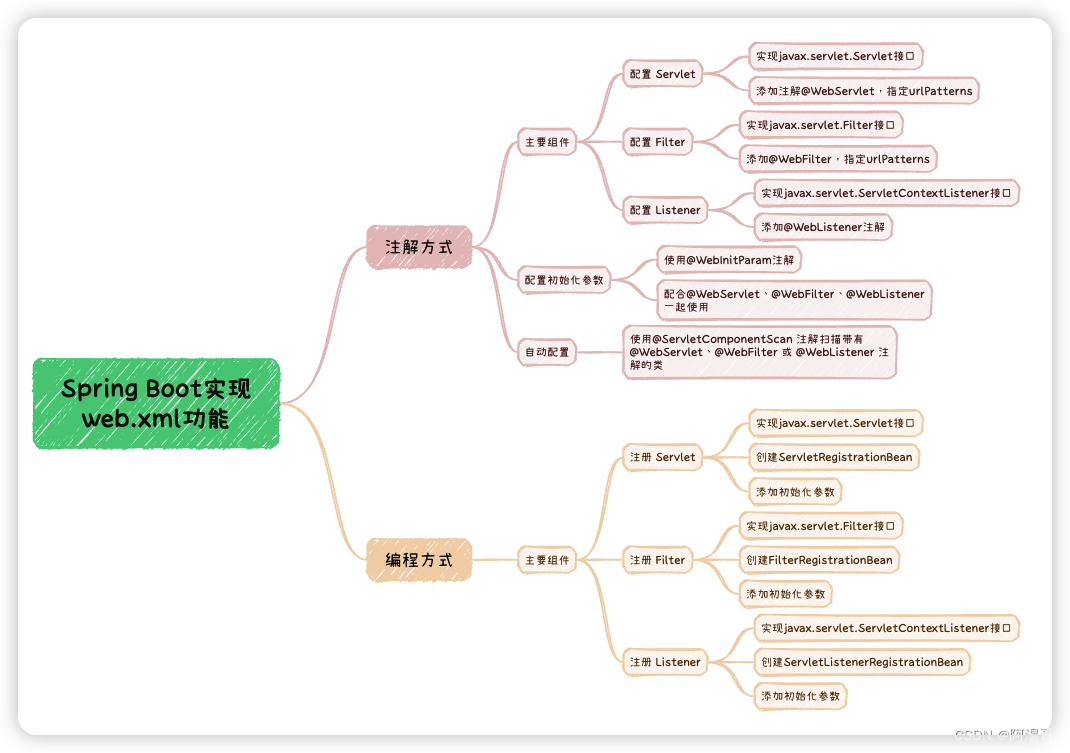
Spring Boot实现web.xml功能
Spring Boot实现web.xml功能 1. 基于注解实现1.1 组件注册1.2 WebInitParam注解 2. 基于编码实现2.1 Servlet & Filter2.2 Listener 3. 总结 在Spring Boot中,不再需要使用传统的 web.xml 文件来配置web应用的功能,Spring Boot支持通过注解和基于代码…...
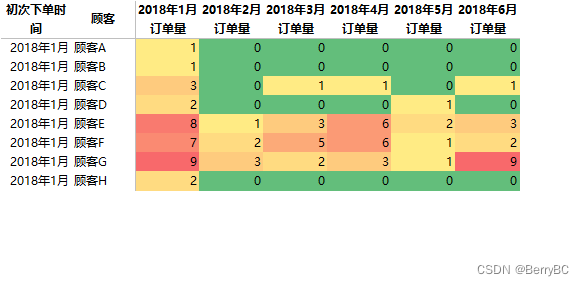
陆拾捌- 如何通过数据影响决策(三)
一、如何正确的引导别人? 引导与误导的区别是什么? 看下面这广告图 单看上面大字的结果,感觉好像真的使用过的人均觉得有好处 可如果我们看下面的细字 对111位连续14天食用(本产品)的燕麦片非重度使用者所做调研… 从…...

VMware 三种网络连接模式
VMware虚拟机的三种网络连接模式:桥接,NAT,仅主机。 网卡vmnet0,vmnet1,vmnet8区别。 在VMware中,虚拟机的网络连接主要是由VMware创建的虚拟交换机负责实现的,VMware可以根据需要创建多个虚拟网络。 VMware的虚拟网…...

Scikit-Learn快速生成分类数据集
假如你学习了新的分类算法并想进一步探索研究、尝试不同的超参数评估模型性能,但问题是你找不到好的数据集用于实验。幸运的是Scikit-Learn 提供的 make_classification() 方法可以创建不同类型的数据集,它可以生成不同类型的数据集:二分类、…...

西门子 S7 协议解析
目录 1 建立连接 2 读数据 3 写数据 1 建立连接 03 00 00 16 11 E0 00 00 00 01 00 C1 02 10 00 C2 02 03 01 C0 01 0A (第一次握手报文) 03 00 报文头 00 16 数据总长度:22 11 E0 00 00 00 01 00 C1 02 10 00 C2 02 03 01 C0 01 0A 报文结束…...

一、python解题——求序列最长递增
解题代码: import os import sys# 请在此输入您的代码 n int(input()) a list(map(int, input().split())) # 创建一个初始元素全为1的列表,用来存放每个递增序列的长度 b [1 for x in range(0, n)] # 设置num,用来控制b列表的下标 num …...

【Java 基础篇】Java线程:volatile关键字与原子操作详解
在多线程编程中,确保线程之间的可见性和数据一致性是非常重要的。Java中提供了volatile关键字和原子操作机制,用于解决这些问题。本文将深入讨论volatile关键字和原子操作的用法,以及它们在多线程编程中的重要性和注意事项。 volatile关键字…...

992. K 个不同整数的子数组
992. K 个不同整数的子数组 给定一个正整数数组 nums和一个整数 k,返回 nums 中 「好子数组」 的数目。 如果 nums 的某个子数组中不同整数的个数恰好为 k,则称 nums 的这个连续、不一定不同的子数组为 「好子数组 」。 例如,[1,2,3,1,2] 中…...

Vue 使用vue-cli构建SPA项目(超详细)
目录 一、什么是vue-cli 二,构建SPA项目 三、 运行SPA项目 前言: 在我们搭建SPA项目时候,我们必须去检查我们是否搭建好NodeJS环境 cmd窗口输入以下指令:去检查 node -v npm -v 一、什么是vue-cli Vue CLI(Vu…...

SpringBoot工程模板
spring脚手架:https://start.spring.io/ <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocati…...
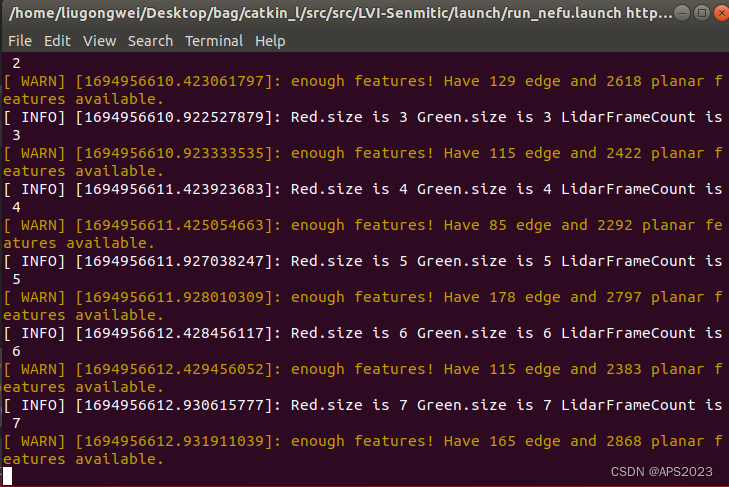
学习SLAM:SLAM进阶(十)暴力更改ROS中的PCL库
话不多说,上活 1.1 为什么要这么做 项目中有依赖。。。。 1.2 安装VTK7.1.1 PCL1.8.0 略 1.3 移植到ROS 删除ROS依赖的vtk6.2和PCL1.8.0的动态链接库: liugongweiubuntu:~$ sudo mv /usr/lib/x86_64-linux-gnu/libvtk* Desktop/lib/ [sudo] password fo…...
)
Hunyuan-MT Pro快速上手:Streamlit缓存机制加速重复翻译响应(Cache层详解)
Hunyuan-MT Pro快速上手:Streamlit缓存机制加速重复翻译响应(Cache层详解) 1. 项目概述:现代化翻译终端 Hunyuan-MT Pro是一个基于腾讯混元开源模型构建的现代化翻译Web终端。它将Streamlit的便捷交互界面与混元模型强大的多语言…...
)
DrissionPage实战:绕过滑块验证的精准定位与模拟操作(非深度学习方案)
1. 为什么选择非深度学习的滑块验证绕过方案 最近在做一个自动化项目时,遇到了滑块验证码这个拦路虎。刚开始我也考虑过用深度学习方案,但实测下来发现几个痛点:首先需要大量标注数据训练模型,其次识别准确率不稳定,最…...

2026年常用CMS系统大全:主流建站内容平台分类与选型指南
“CMS”是内容管理系统(Content Management System)的缩写。常用的CMS通常根据主要应用领域(如网站搭建、企业门户、电子商务、文档管理)来划分。 以下是目前最主流、最常用的几类CMS(按技术生态和用途分类)…...

GTE-Pro企业知识库迁移指南:从关键词检索平滑升级至语义检索架构
GTE-Pro企业知识库迁移指南:从关键词检索平滑升级至语义检索架构 1. 迁移背景与价值 传统的关键词检索系统在企业知识库中已经服务多年,它们基于简单的文字匹配原理工作:你输入什么词,系统就找包含这些词的文档。这种方法虽然简…...
)
Dify Token监控必须绕开的7个K8s原生监控坑(含cAdvisor指标失真、HorizontalPodAutoscaler误判、etcd lease泄漏详解)
第一章:Dify Token监控必须绕开的7个K8s原生监控坑(含cAdvisor指标失真、HorizontalPodAutoscaler误判、etcd lease泄漏详解)在 Dify 这类高并发、长生命周期 Token 管理场景中,直接复用 Kubernetes 原生监控组件极易导致 Token 耗…...

中小企业影像修复方案:cv_unet_image-colorization低成本部署教程
中小企业影像修复方案:cv_unet_image-colorization低成本部署教程 1. 项目简介与核心价值 在数字化时代,许多中小企业都面临着历史影像资料修复的需求。老照片、档案图片、历史文档等黑白影像的彩色化,不仅能提升视觉体验,更能为…...

保姆级SAM 3入门指南:上传图片输入英文,轻松实现物体识别分割
保姆级SAM 3入门指南:上传图片输入英文,轻松实现物体识别分割 你是不是经常遇到这样的场景?看到一张精美的图片,想单独提取出里面的某个物体,比如一只可爱的猫、一本书,或者一个特别的Logo。手动抠图&…...

从选题到成稿零焦虑:Paperzz 毕业论文初稿写作,让学术创作告别 “卡壳式内耗”
Paperzz-AI官网免费论文查重复率AIGC检测/开题报告/文献综述/论文初稿paperzz - 毕业论文-AIGC论文检测-AI智能降重-ai智能写作https://www.paperzz.cc/dissertation 在毕业论文的漫长写作路上,你是否也陷入过这样的循环:对着空白文档发呆半天写不出开头…...

Qwen2.5-1.5B GPU算力优化教程:torch_dtype=auto与device_map智能分配详解
Qwen2.5-1.5B GPU算力优化教程:torch_dtypeauto与device_map智能分配详解 1. 为什么需要GPU算力优化 当你第一次在本地运行Qwen2.5-1.5B这样的语言模型时,可能会遇到显存不足或者计算速度慢的问题。特别是在使用消费级显卡或者低配GPU环境时࿰…...

Ollama本地化部署DeepSeek指南:从零到高效运行
1. 为什么要在本地跑大模型?从Ollama和DeepSeek说起 最近两年,AI大模型火得一塌糊涂,但说实话,每次用那些在线服务,我心里总有点不踏实。一个是网络问题,关键时刻掉链子急死人;另一个是隐私&…...
