LC1713. 得到子序列的最少操作次数(java - 动态规划)
LC1713. 得到子序列的最少操作次数
- 题目描述
- LIS 动态规划 + 二分法
- 代码演示
题目描述
难度 - 困难
LC1713.得到子序列的最少操作次数
给你一个数组 target ,包含若干 互不相同 的整数,以及另一个整数数组 arr ,arr 可能 包含重复元素。
每一次操作中,你可以在 arr 的任意位置插入任一整数。比方说,如果 arr = [1,4,1,2] ,那么你可以在中间添加 3 得到 [1,4,3,1,2] 。你可以在数组最开始或最后面添加整数。
请你返回 最少 操作次数,使得 target 成为 arr 的一个子序列。
一个数组的 子序列 指的是删除原数组的某些元素(可能一个元素都不删除),同时不改变其余元素的相对顺序得到的数组。比方说,[2,7,4] 是 [4,2,3,7,2,1,4] 的子序列(加粗元素),但 [2,4,2] 不是子序列。
示例 1:
输入:target = [5,1,3], arr = [9,4,2,3,4]
输出:2
解释:你可以添加 5 和 1 ,使得 arr 变为 [5,9,4,1,2,3,4] ,target 为 arr 的子序列。
示例 2:
输入:target = [6,4,8,1,3,2], arr = [4,7,6,2,3,8,6,1]
输出:3
提示:
1 <= target.length, arr.length <= 10^5
1 <= target[i], arr[i] <= 10^9
target 不包含任何重复元素。
LIS 动态规划 + 二分法
为了方便,我们令 target 长度为 n,arr 长度为 m,target 和 arr 的最长公共子序列长度为 max,不难发现最终答案为 n−max。
因此从题面来说,这是一道最长公共子序列问题(LCS)。
但朴素求解 LCS 问题复杂度为 O(n∗m),使用状态定义「f[i][j] 为考虑 a 数组的前 i 个元素和 b 数组的前 j 个元素的最长公共子序列长度为多少」进行求解。
而本题的数据范围为 10^5,使用朴素求解 LCS 的做法必然超时。
一个很显眼的切入点是 target 数组元素各不相同,当 LCS 问题增加某些条件限制之后,会存在一些很有趣的性质。
其中一个经典的性质就是:当其中一个数组元素各不相同时,最长公共子序列问题(LCS)可以转换为最长上升子序列问题(LIS)进行求解。同时最长上升子序列问题(LIS)存在使用「维护单调序列 + 二分」的贪心解法,复杂度为 O(nlogn)。
因此本题可以通过「抽象成 LCS 问题」->「利用 target数组元素各不相同,转换为 LIS 问题」->「使用 LIS 的贪心解法」,做到 O(nlogn) 的复杂度。
朴素的 LIS 问题求解,我们需要定义一个 f[i] 数组代表以 nums[i] 为结尾的最长上升子序列的长度为多少。
对于某个 f[i] 而言,我们需要往回检查 [0,i−1] 区间内,所有可以将 nums[i] 接到后面的位置 jjj,在所有的 f[j]+1中取最大值更新 f[i]。因此朴素的 LIS 问题复杂度是 O(n^2) 的。
LIS 的贪心解法则是维护一个额外 ggg 数组,g[len]=x 代表上升子序列长度为 lenlenlen 的上升子序列的「最小结尾元素」为 x。
整理一下,我们总共有两个数组:
- f 动规数组:与朴素 LIS 解法的动规数组含义一致。f[i]f[i]f[i] 代表以 nums[i] 为结尾的上升子序列的最大长度;
- g 贪心数组:g[len]=x代表上升子序列长度为 len 的上升子序列的「最小结尾元素」为 x。
由于我们计算 f[i] 时,需要找到满足 nums[j]<nums[i],同时取得最大 f[j] 的位置 j。
我们期望通过 g 数组代替线性遍历。
显然,如果 g 数组具有「单调递增」特性的话,我们可以通过「二分」找到符合 g[idx]<nums[i] 分割点 idxi(下标最大),即利用 O(logn) 复杂度找到最佳转移位置。
代码演示
class Solution {public int minOperations(int[] target , int[] arr) {Map<Integer, Integer> map = new HashMap();int Tlen = target.length, Alen = arr.length;//1:target的元素和对应下标 装入mapfor(int i = 0; i < Tlen; i++) map.put(target[i], i);//2:在arr中寻找相等的值的下标装入下标数组int[] index = new int[Alen];int p = 0;for(int i = 0; i < Alen; i++){if(map.containsKey(arr[i])) index[p++] = map.get(arr[i]);}//3:直接调用处理最长递增公共子串代码(之前做过,这里赋值过来,偷懒)int uplen = lengthOfLIS(index,p);return Tlen - uplen;}public int lengthOfLIS(int[] nums,int n){if(n == 0) return 0;int res = 1;int[] dp = new int[n];dp[0] = nums[0];for(int num:nums){int i = 0,j = res;while(i < j){int mid = (i + j)>>1;if(dp[mid] >= num) j = mid;else i = mid + 1;}dp[i] = num;if(j == res) res++;}return res;}}
相关文章:

LC1713. 得到子序列的最少操作次数(java - 动态规划)
LC1713. 得到子序列的最少操作次数 题目描述LIS 动态规划 二分法代码演示 题目描述 难度 - 困难 LC1713.得到子序列的最少操作次数 给你一个数组 target ,包含若干 互不相同 的整数,以及另一个整数数组 arr ,arr 可能 包含重复元素。 每一次…...
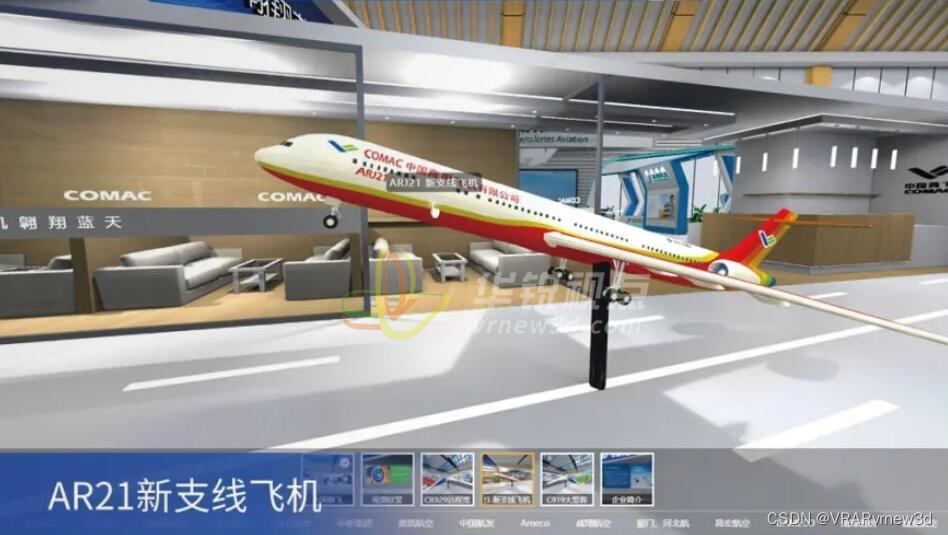
vr飞机驾驶舱模拟流程3D仿真演示加大航飞安全法码
众所周知,航空航天飞行是一项耗资大、变量参数很多、非常复杂的系统工程,因此可利用虚拟仿真技术经济、安全及可重复性等特点,进行飞行任务或操作的模拟,以代替某些费时、费力、费钱的真实试验或者真实试验无法开展的场合…...
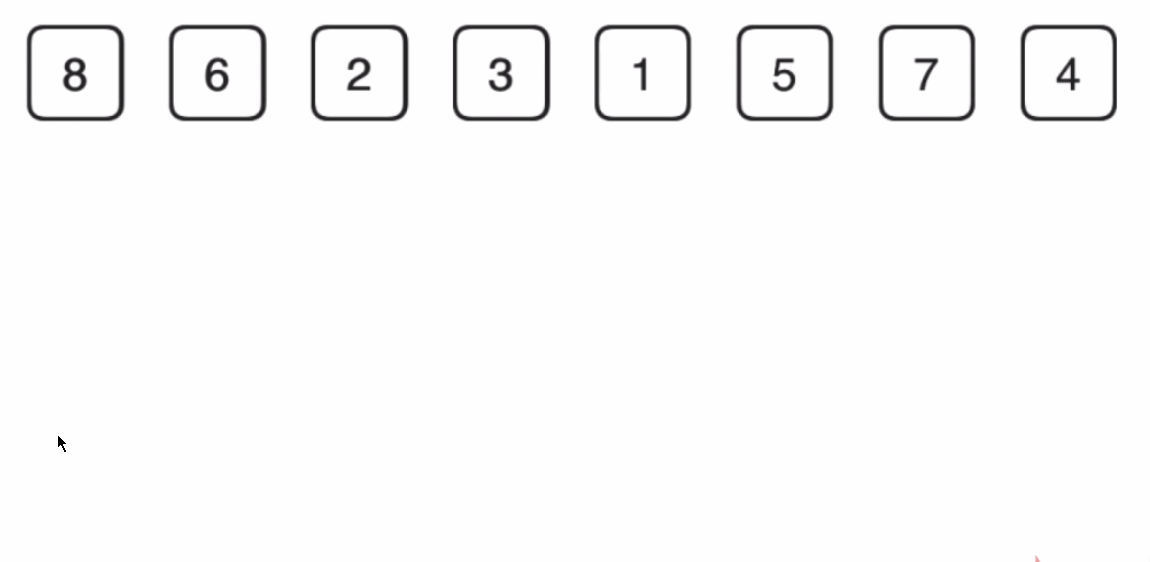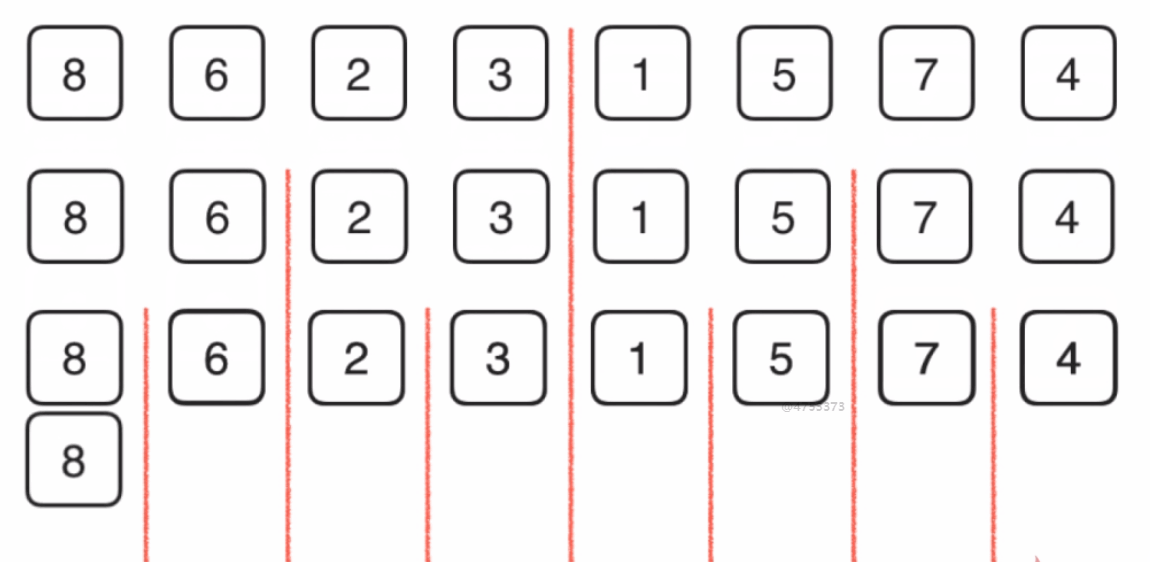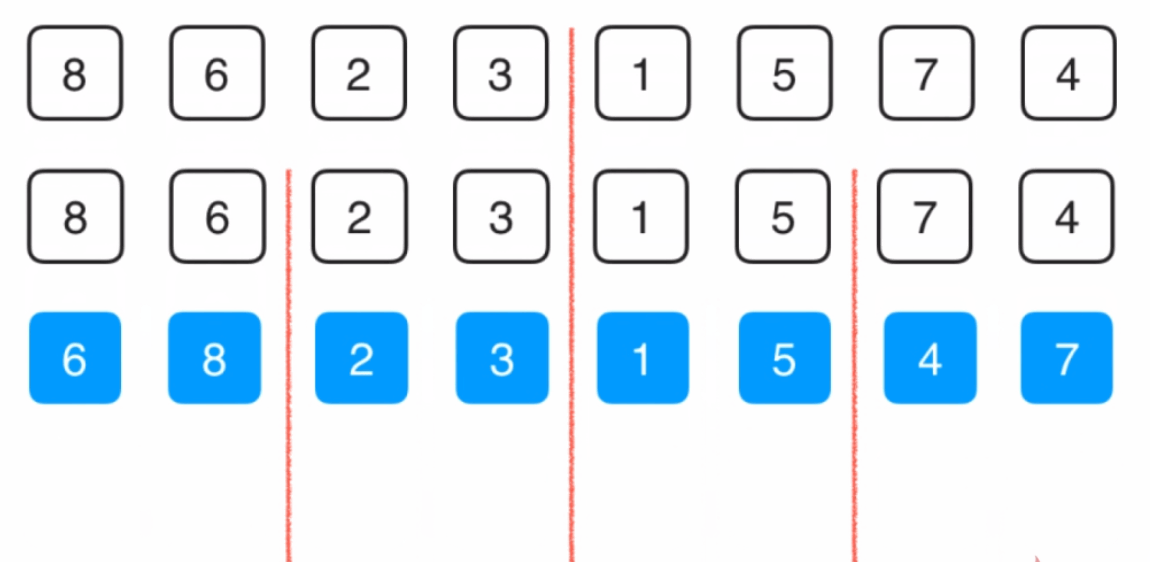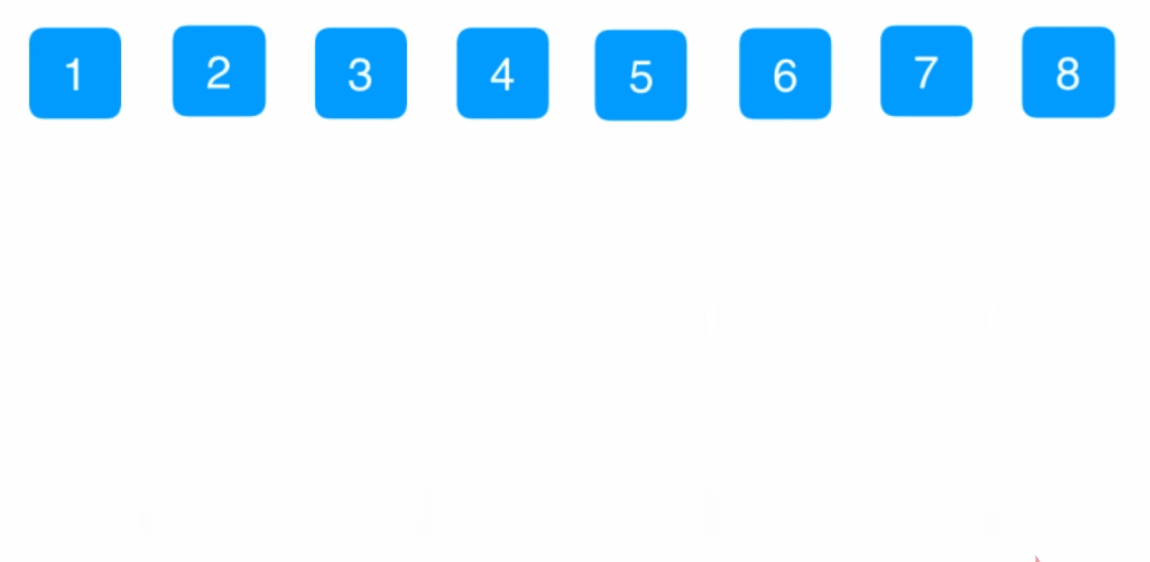
一、八大排序(sort)
文章目录 一、时间复杂度(一)定义:常数操作 二、空间复杂度(一)定义: 三、排序(一)选择排序1.定义2.代码3.特性 (二)冒泡排序1.定义2.代码3.特性 (…...
【AWS】AI 代码生成器—Amazon CodeWhisperer初体验 | 开启开挂编程之旅
使用 AI 编码配套应用程序更快、更安全地构建应用程序 文章目录 1.1 Amazon CodeWhisperper简介1.2 Amazon CodeWhisperer 定价2.1 打开VS Code2.2 安装AWS ToolKit插件 一、前言 1.1 Amazon CodeWhisperper简介 1️⃣更快地完成更多工作 CodeWhisperer 经过数十亿行代码的训…...

【Mysql主从配置方法---单主从】
Mysql主从 主服务器 创建用户 create user “for_rep”“从服务器IP地址” IDENTIFIED by “123456” 授权 grant replication slave on . to “for_rep”“从服务器IP地址” IDENTIFIED by “123456” 查看用户权限 SHOW GRANTS FOR “for_rep”“从服务器IP地址”; 修改M…...

⼀⽂读懂加密资产交易赛道的新锐⼒量Bitdu
交易所,仍然是加密资产赛道的皇冠级赛道。围绕这个领域展开的商业竞争,最能引起⼴⼤⽤⼾的关注。 经历了数轮资产价格涨跌的⽜熊之后,⼀批批创业者也在不断地思考这⼀议题 — 如何在去中⼼化的世界中,最⾼效率地集结流量、资本和…...
万里牛与金蝶云星空对接集成查询调拨单连通调拨单新增(万里牛调拨单-金蝶【直接调拨单】)
万里牛与金蝶云星空对接集成查询调拨单连通调拨单新增(万里牛调拨单-金蝶【直接调拨单】) 源系统:万里牛 万里牛是杭州湖畔网络技术有限公司旗下SaaS软件品牌,主要针对电商、外贸、实体门店等业务群体,帮助企业快速布局新零售,提升订单处理效…...
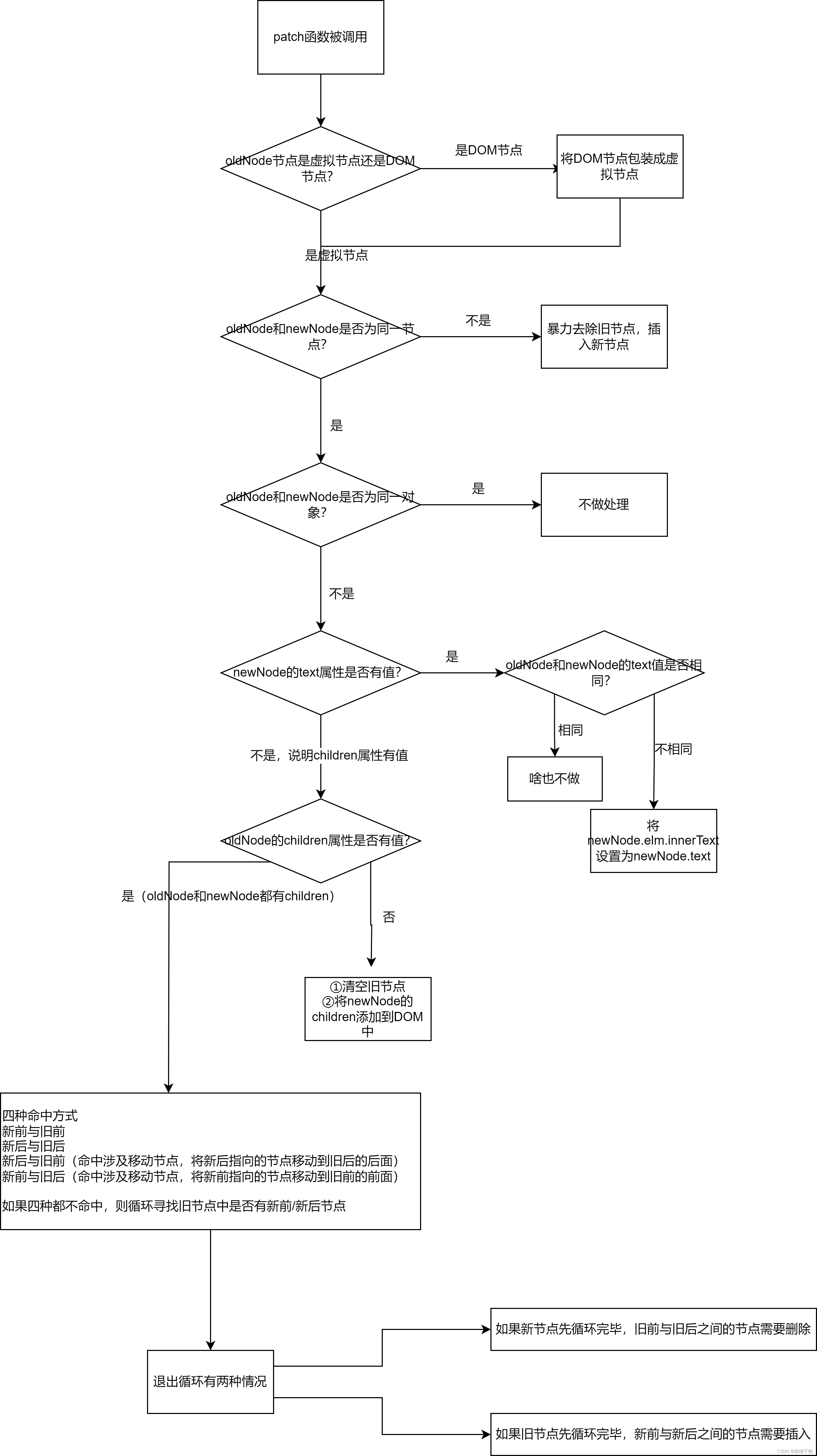
虚拟DOM与diff算法
虚拟DOM与diff算法 snabbdom虚拟DOMdiff算法 snabbdom 是什么:snabbdom是著名的虚拟DOM库,是diff算法的鼻祖,Vue源码借鉴了snabbdom 虚拟DOM 是什么:本质上是存在内存里的 JavaScript 对象 作用:用来描述真实DOM的层…...

K8S:pod资源限制及探针
文章目录 一.pod资源限制1.pod资源限制方式2.pod资源限制指定时指定的参数(1)request 资源(2) limit 资源(3)两种资源匹配方式 3.资源限制的示例(1)官网示例(2࿰…...

CSS中的定位
position 的属性与含义 CSS 中的 position 属性用于控制元素在页面中的定位方式,有四个主要的取值,每个取值都会影响元素的布局方式,它们是: static(默认值): 这是所有元素的初始定位方式。在静…...
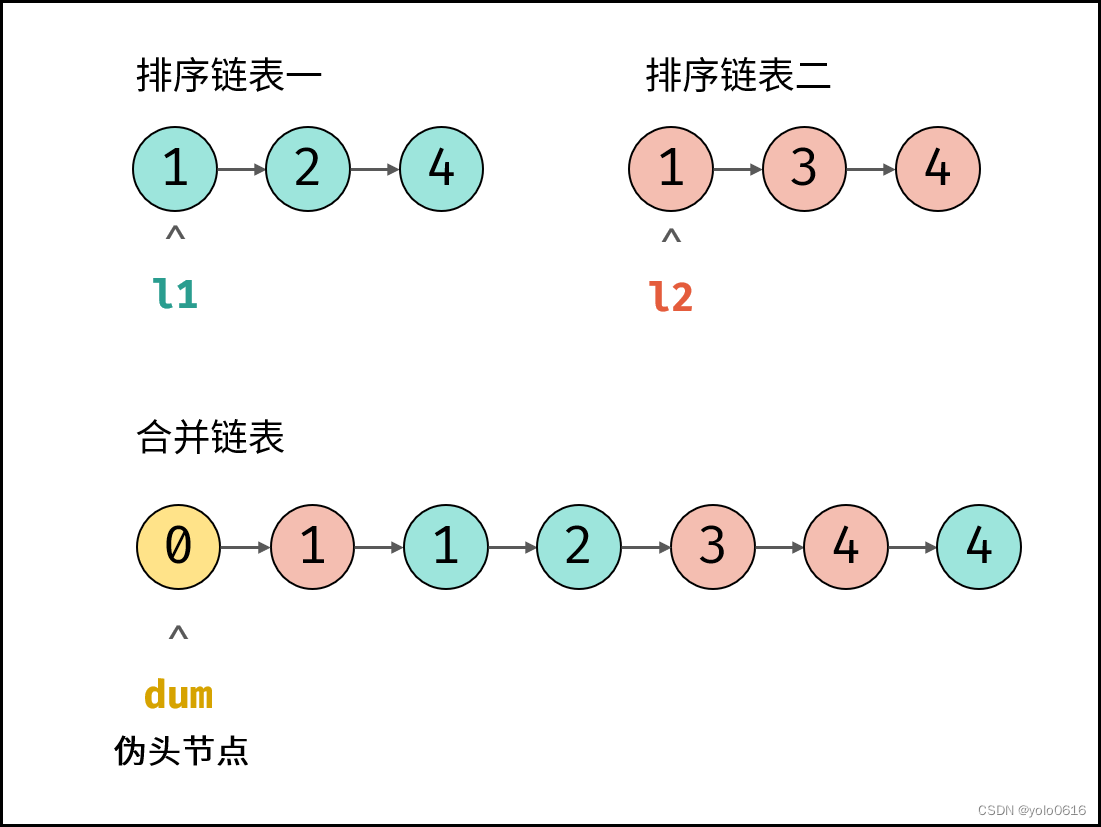
二、链表(linked-list)
文章目录 一、定义二、经典例题(一)[21.合并两个有序链表](https://leetcode.cn/problems/merge-two-sorted-lists/description/)1.思路2.复杂度分析3.注意4.代码 (二)[86.分割链表](https://leetcode.cn/problems/partition-list…...
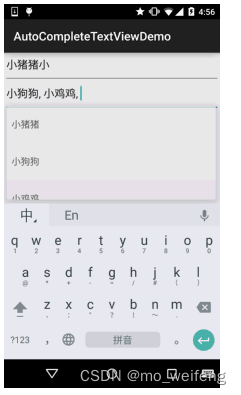
Android EditText筛选+选择功能开发
在日常开发中经常会遇到这种需求,EditText既需要可以筛选,又可以点击选择。这里筛选功能用的是AutoCompleteTextView,选择功能使用的是第三方库https://github.com/kongzue/DialogX。 Android AutoCompleteTextView(自动完成文本框)的基本使用…...

Linux 信号 alarm函数 setitimer函数
/*#include <unistd.h>unsigned int alarm(unsigned int seconds);功能:设置定时器。函数调用,开始倒计时,0的时候给当前的进程发送SIGALARM信号参数:倒计时的时长。。单位:秒 如果参数为0,无效返回…...

自主设计,模拟实现 RabbitMQ - 实现发送方消息确认机制
目录 一、实现发送方消息确认 1.1、需求分析 什么是发送方的消息确认? 如何实现?...

【数据结构】二叉树的·深度优先遍历(前中后序遍历)and·广度优先(层序遍历)
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...
优彩云采集器下载-免费优彩云采集器下载地址
免费优彩云采集器。您是否曾为了数据采集而感到头疼不已?是否一直在寻找一种能够轻松、高效地获取所需数据的方法?别着急,让我们一起来了解如何通过优彩云采集器解决这些问题,从而让您产生购买的欲望。 免费全自动采集发布批量管理…...

【Python】OJ 常用函数
这里写目录标题 一. math1. 求阶乘 - factorial()2. 绝对值 - fabs() 二. 容器的方法1. reverse() 三. Python 内置函数1. sort() 一. math 需要引入 math 包:import math 1. 求阶乘 - factorial() import math print(math.factorial(5))--------运行结果-------…...

【Vue】上万个字把事件处理讲解的淋漓尽致
hello,我是小索奇,精心制作的Vue系列教程持续更新哈,想要学习&巩固&避坑就一起学习吧~ 事件处理 事件的基本用法 重点内容 使用v-on:xxx缩写xxx绑定事件,其中 xxx 是事件名(回顾:v-bind缩写为冒号…...

Remmina中VNC、SSH和RDP的区别
Remmina 可以在 Linux 系统上对远程进行连接。它支持多种远程连接协议,包括 VNC(Virtual Network Computing)、SSH(Secure Shell)和 RDP(Remote Desktop Protocol)。这些协议用于实现不同类型的…...
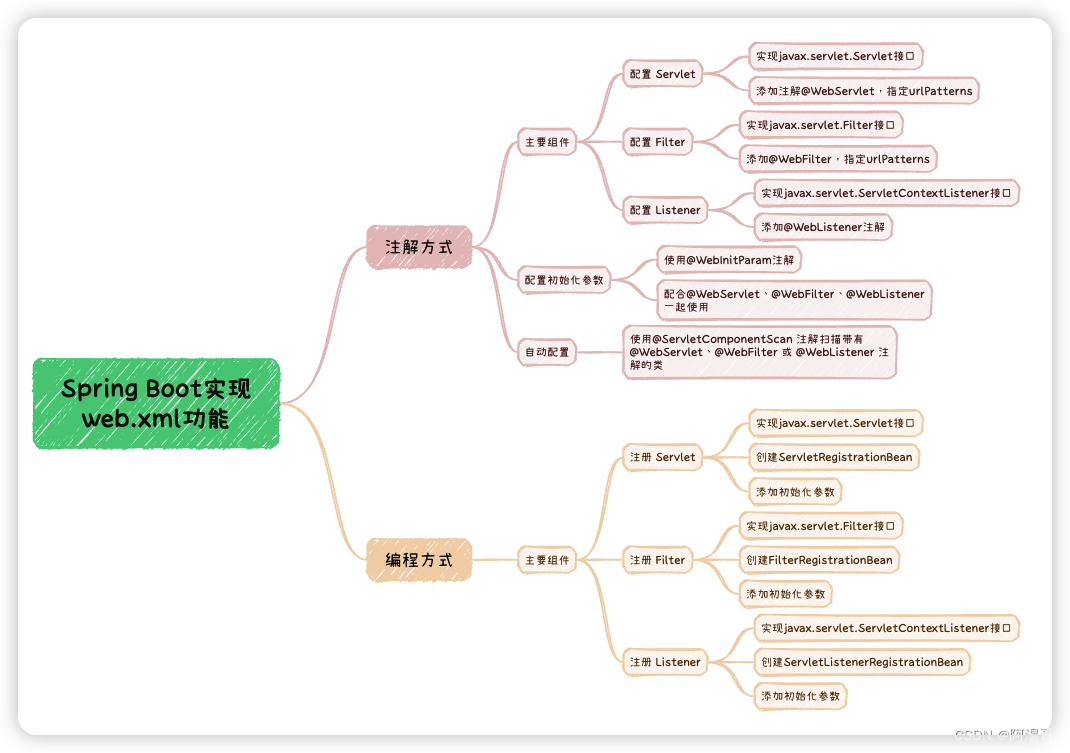
Spring Boot实现web.xml功能
Spring Boot实现web.xml功能 1. 基于注解实现1.1 组件注册1.2 WebInitParam注解 2. 基于编码实现2.1 Servlet & Filter2.2 Listener 3. 总结 在Spring Boot中,不再需要使用传统的 web.xml 文件来配置web应用的功能,Spring Boot支持通过注解和基于代码…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
