怒刷LeetCode的第11天(Java版)
目录
第一题
题目来源
题目内容
解决方法
方法一:迭代
方法二:递归
方法三:指针转向
第二题
题目来源
题目内容
解决方法
方法一:快慢指针
方法二:Arrays类的sort方法
方法三:计数器
方法四:额外的数组
第三题
题目来源
题目内容
解决方法
方法一:双指针
方法二:List
方法三:交换元素
方法四:递归
第一题
题目来源
25. K 个一组翻转链表 - 力扣(LeetCode)
题目内容
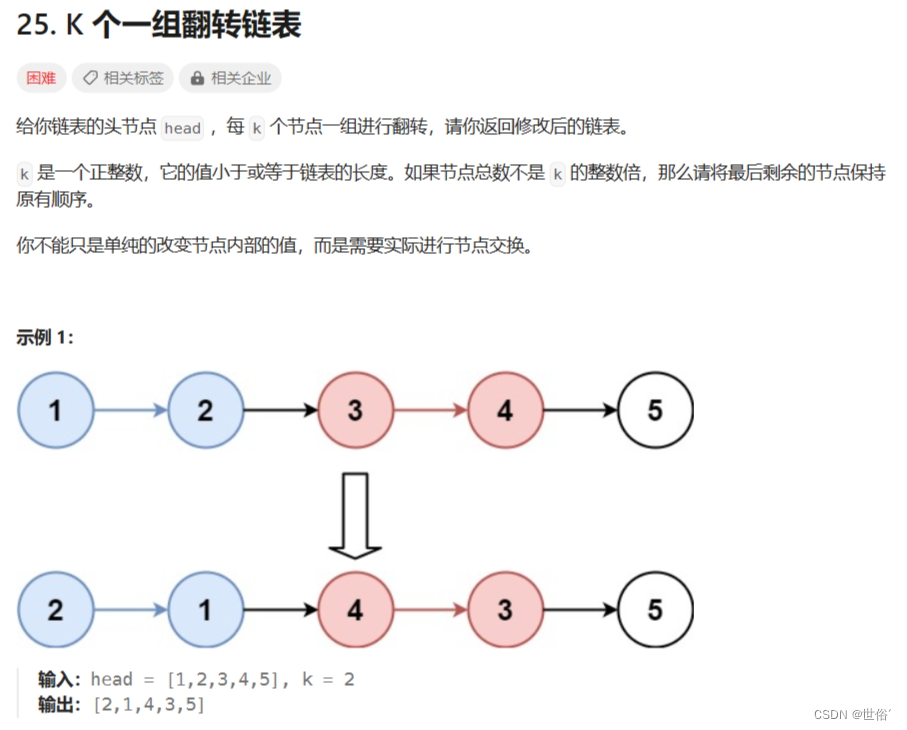
解决方法
方法一:迭代
题目描述中要求将链表每 k 个节点作为一组进行翻转。这是一个比较经典的链表问题,可以使用迭代的方法来解决。具体思路如下:
- 首先定义两个指针 prev 和 curr,分别指向当前组的前一个节点和当前节点。
- 使用一个计数器 count 来记录当前组中已经遍历的节点数目。
- 遍历链表,对于每个节点 curr:
- 将 curr 的下一个节点保存到 next。
- 如果 count 等于 k,则说明当前组内的节点已经遍历完毕,需要进行翻转。具体操作如下:
- 调用 reverse 函数对 prev 和 curr 之间的节点进行翻转,返回翻转后的头节点,并将它赋值给新的 prev。
- 将翻转后的最后一个节点的 next 指向 next,即连接下一组的头节点。
- 更新 curr 和 prev,将它们都指向 next。
- 将 count 重置为 0,表示下一组的遍历开始。
- 如果 count 不等于 k,则说明当前组内的节点还未满 k 个,继续遍历下一个节点。
- 将 curr 更新为 next,继续遍历下一个节点。
- 将 count 增加 1。
- 返回翻转后的链表头节点。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {ListNode dummy = new ListNode(0);dummy.next = head;ListNode prev = dummy;ListNode curr = head;int count = 0;while (curr != null) {count++;ListNode next = curr.next;if (count == k) {prev = reverse(prev, next);count = 0;}curr = next;}return dummy.next;
}private ListNode reverse(ListNode start, ListNode end) {ListNode prev = start;ListNode curr = start.next;ListNode first = curr;while (curr != end) {ListNode next = curr.next;curr.next = prev;prev = curr;curr = next;}start.next = prev;first.next = curr;return first;
}}复杂度分析:
时间复杂度分析:
- 遍历链表需要 O(n) 的时间,其中 n 是链表的长度。
- 在每个节点组内进行翻转操作时,需要遍历 k 个节点,即 O(k) 的时间复杂度。
- 总共有 n/k 个节点组,所以翻转操作的总时间复杂度是 O((n/k) * k) = O(n)。
因此,总的时间复杂度是 O(n)。
空间复杂度分析:
- 我们只使用了常数级别的额外空间,例如指针变量和辅助节点。
- 因此,空间复杂度是 O(1)。
综上所述,该解法的时间复杂度为 O(n),空间复杂度为 O(1)。
LeetCode运行结果:
方法二:递归
除了迭代的解法,还可以使用递归的思路来实现链表的翻转。
具体的递归思路如下:
- 定义一个函数
reverseKGroupRecursive,其功能是将以head为头节点的链表每 k 个节点进行翻转,并返回翻转后的链表的头节点。 - 首先遍历链表,找到第 k+1 个节点
next。- 如果
next!=null,说明当前组内有至少 k 个节点,可以进行翻转操作。- 调用
reverse函数对以head为头节点、以next为尾节点的子链表进行翻转,并将翻转后的尾节点返回,将其赋值给newHead。 - 将
head的 next 指针指向下一组的头节点,即调用reverseKGroupRecursive(next, k)。 - 返回
newHead,作为翻转后的链表的头节点。
- 调用
- 如果
next==null,说明剩余的节点数少于 k 个,无需翻转,直接返回head。
- 如果
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {ListNode curr = head;int count = 0;while (curr != null && count < k) {curr = curr.next;count++;}if (count == k) {ListNode newHead = reverseKGroupRecursive(head, curr, k);head.next = reverseKGroup(curr, k);return newHead;}return head;
}private ListNode reverseKGroupRecursive(ListNode head, ListNode tail, int k) {ListNode prev = tail;ListNode curr = head;while (curr != tail) {ListNode next = curr.next;curr.next = prev;prev = curr;curr = next;}return prev;
}}复杂度分析:
时间复杂度分析:
- 遍历链表需要 O(n) 的时间,其中 n 是链表的长度。
- 递归调用了 n/k 次,每次都需要翻转 k 个节点,因此每次递归操作的时间复杂度是 O(k)。
- 整个算法的时间复杂度是 O((n/k) * k) = O(n)。
因此,总的时间复杂度是 O(n)。
空间复杂度分析:
- 递归的深度是 n/k,因此递归调用栈的最大深度是 O(n/k)。
- 每次递归操作需要常数级别的额外空间,例如指针变量和辅助节点。
- 因此,空间复杂度是 O(n/k),在最坏情况下为 O(n)。需要注意的是,在实际使用中链表长度较大时,递归方法可能会导致递归调用栈溢出。
综上所述,递归解法的时间复杂度为 O(n),空间复杂度为 O(n/k)(在最坏情况下为 O(n))。
需要注意的是,递归方法对于链表长度较大时可能会导致递归调用栈溢出,因此在实际使用中需要注意链表长度是否适合使用递归解法。
LeetCode运行结果:
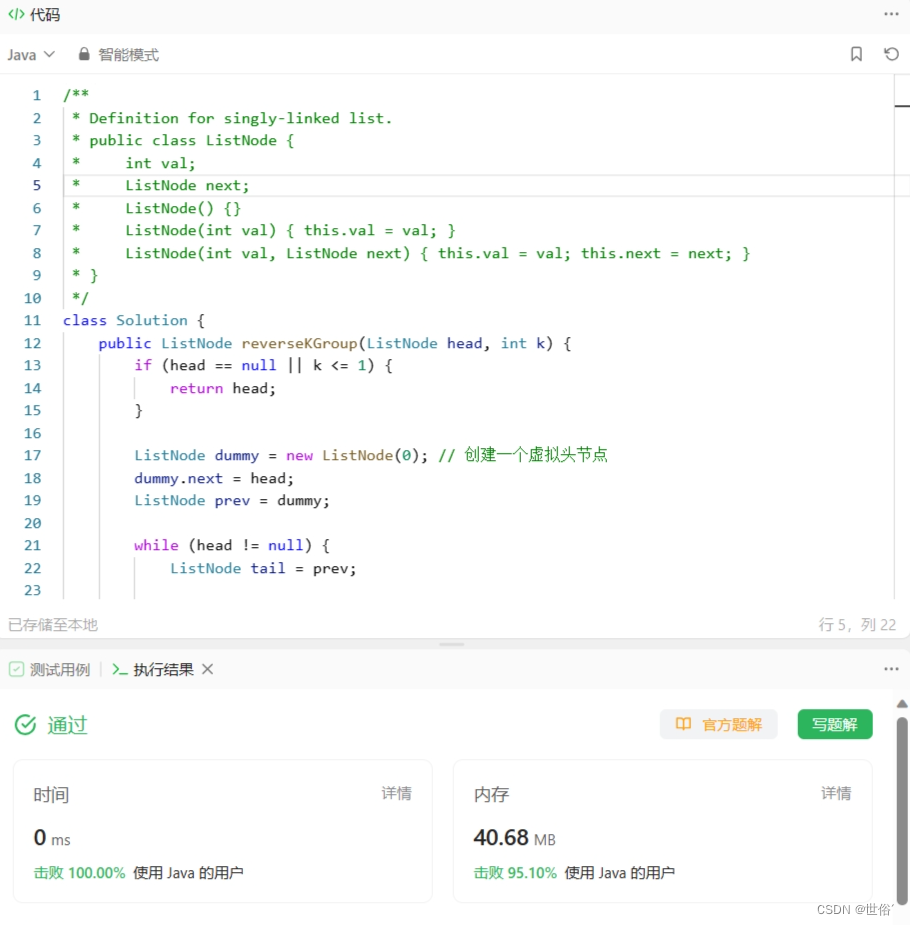
方法三:指针转向
除了迭代、递归的方法,还可以使用指针转向的思路来实现链表的翻转。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode reverseKGroup(ListNode head, int k) {if (head == null || k <= 1) {return head;}ListNode dummy = new ListNode(0); // 创建一个虚拟头节点dummy.next = head;ListNode prev = dummy;while (head != null) {ListNode tail = prev;// 判断剩余节点数是否大于等于 kfor (int i = 0; i < k; i++) {tail = tail.next;if (tail == null) {// 剩余的节点数不满 k 个,直接返回结果return dummy.next;}}ListNode nextGroupHead = tail.next; // 下一组节点的头节点// 翻转当前组内的节点ListNode[] reversed = reverse(head, tail);head = reversed[0];tail = reversed[1];// 将翻转后的组连接到结果链表中prev.next = head;tail.next = nextGroupHead;// 更新 prev 和 head,准备处理下一组prev = tail;head = nextGroupHead;}return dummy.next;}private ListNode[] reverse(ListNode head, ListNode tail) {ListNode prev = tail.next;ListNode curr = head;while (prev != tail) {ListNode next = curr.next;curr.next = prev;prev = curr;curr = next;}return new ListNode[] {tail, head};}
}
该方法通过指针转向的方式,每次翻转一组的节点。其中,reverse 方法用于翻转当前组内的节点。
复杂度分析:
时间复杂度分析:
- 翻转一组的时间复杂度为 O(k),其中 k 是每组节点的数量。
- 对于包含 n 个节点的链表,一共有 n/k 组需要翻转。
- 因此,总的时间复杂度为 O((n/k) * k) = O(n)。
空间复杂度分析:
- 空间复杂度取决于额外使用的变量和递归调用栈的空间。
- 额外使用的变量有 dummy、prev、tail 和 nextGroupHead,它们占用的空间是常数级别的,因此不会随着输入规模 n 的增加而增加。
- 在递归实现中,递归调用栈的深度最多为 n/k,因为总共有 n/k 组需要翻转。
- 因此,递归调用栈的空间复杂度为 O(n/k)。
- 综上所述,总的空间复杂度为 O(1)。
综合来说,该方法的时间复杂度为 O(n),空间复杂度为 O(1)。需要注意的是,在处理不满 k 个节点的情况时,需要额外判断并返回结果。
LeetCode运行结果:
第二题
题目来源
26. 删除有序数组中的重复项 - 力扣(LeetCode)
题目内容


解决方法
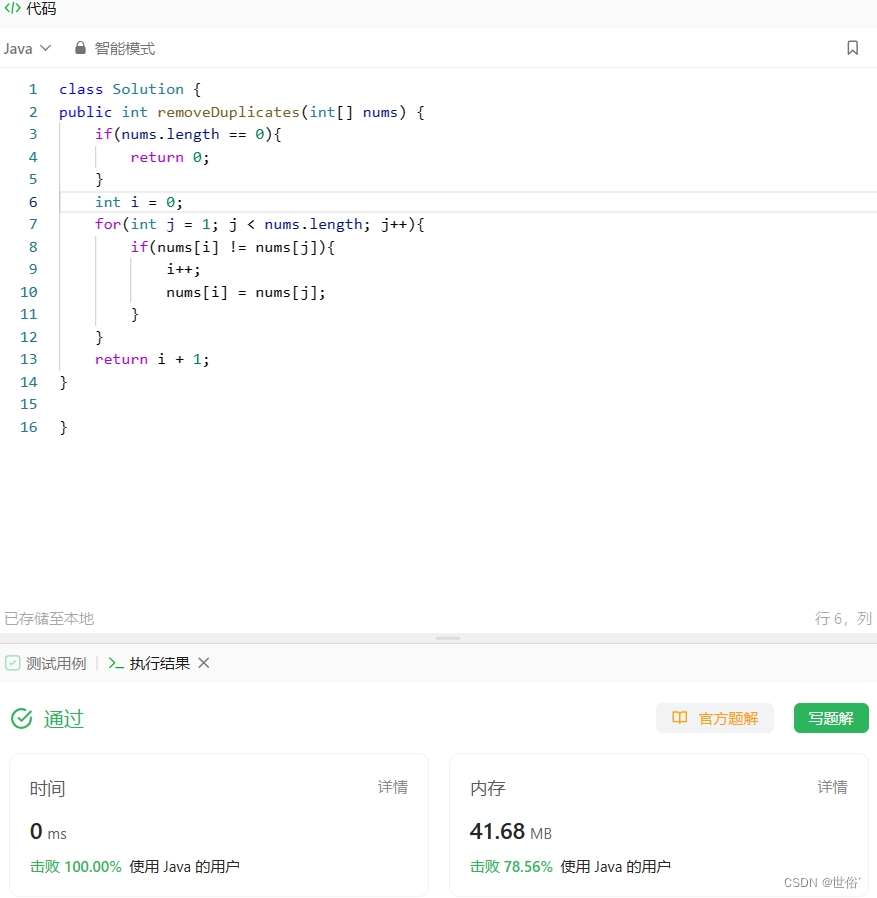
方法一:快慢指针
由于数组已经按非严格递增排列,可以利用快慢指针来遍历数组。慢指针指向当前不重复的元素,快指针用于遍历整个数组。如果快指针指向的元素与慢指针指向的元素不同,说明找到了一个新的不重复元素,将其存放在慢指针的下一个位置,并将慢指针后移一位。最后返回慢指针加1即可。
class Solution {
public int removeDuplicates(int[] nums) {if(nums.length == 0){return 0;}int i = 0;for(int j = 1; j < nums.length; j++){if(nums[i] != nums[j]){i++;nums[i] = nums[j];}}return i + 1;
}}复杂度分析:
-
时间复杂度:O(n),其中n为数组的长度。该算法通过使用快慢指针,只需一次遍历数组即可完成操作。
-
空间复杂度:O(1)。该算法只使用了常数级的额外空间,不随输入规模的增加而增加。
LeetCode运行结果:
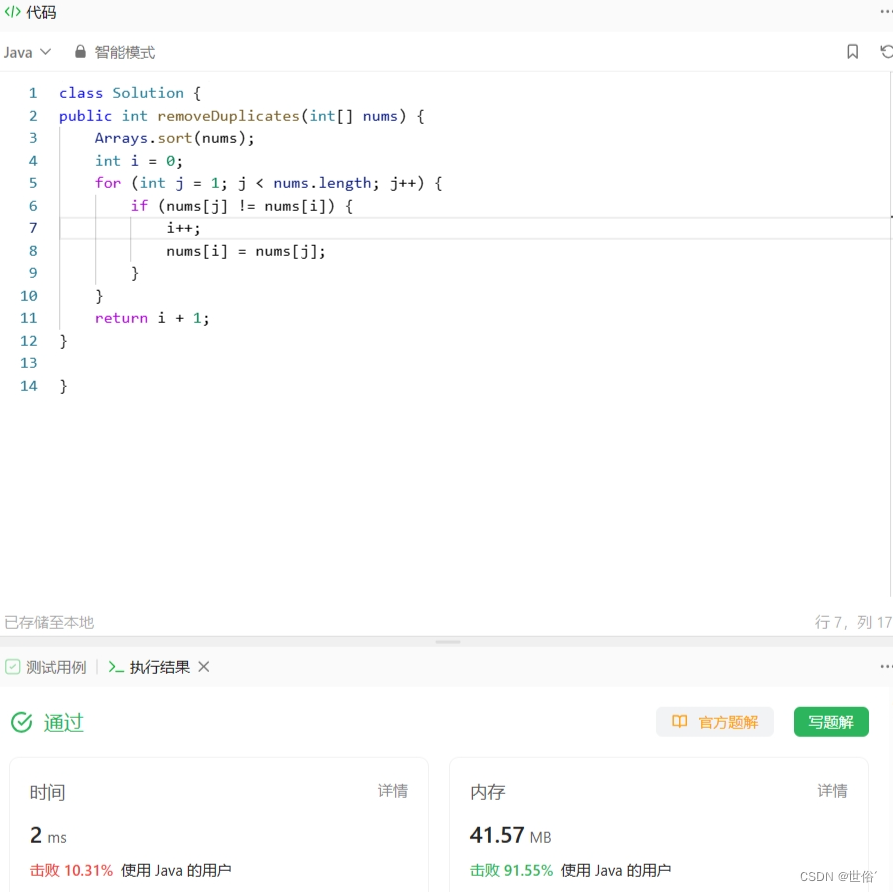
方法二:Arrays类的sort方法
除了使用快慢指针的解法外,在Java中还可以使用Arrays类的sort方法来解决该问题。
该方法首先对数组进行排序,使得重复元素相邻。然后使用快慢指针的方法遍历数组,将不重复的元素放到慢指针所指向的位置,并移动慢指针。最后返回慢指针加1作为新数组的长度。
class Solution {
public int removeDuplicates(int[] nums) {Arrays.sort(nums);int i = 0;for (int j = 1; j < nums.length; j++) {if (nums[j] != nums[i]) {i++;nums[i] = nums[j];}}return i + 1;
}}复杂度分析:
- 时间复杂度:O(n log n),其中n为数组的长度。排序需要O(n log n)的时间复杂度,遍历数组需要O(n)的时间复杂度。
- 空间复杂度:O(1),原地修改数组,不需要额外的空间。
LeetCode运行结果:
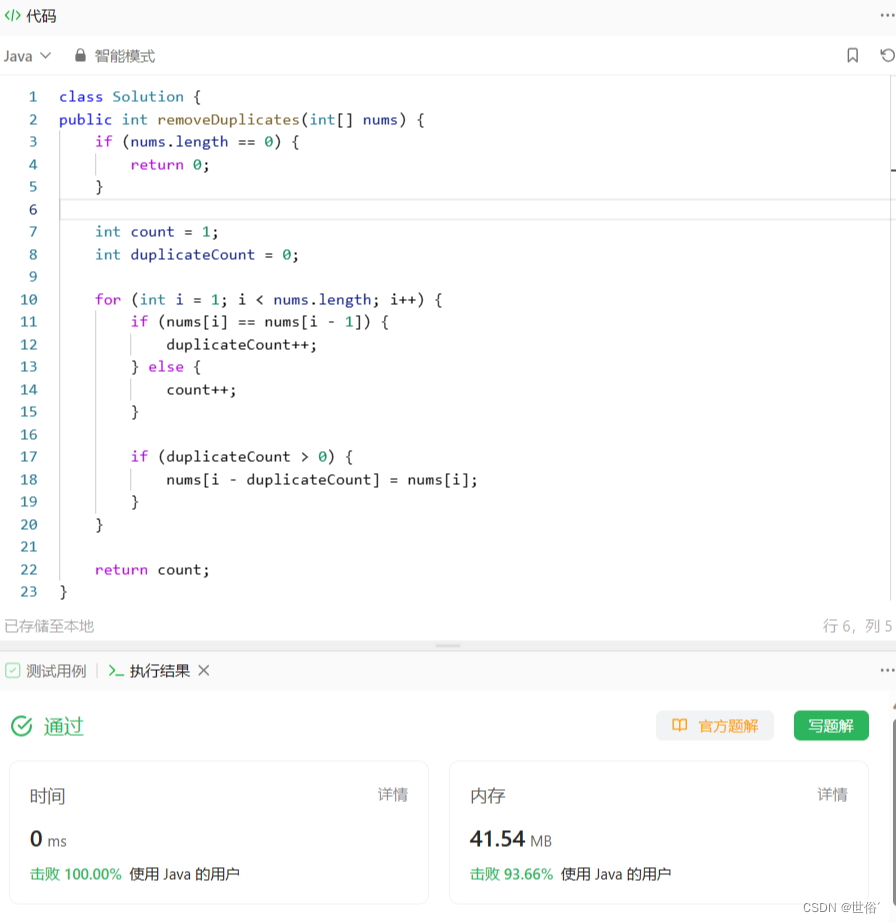
方法三:计数器
除了前面提到的思路和方法,还可以使用一个计数器来记录重复元素的个数,并根据计数器的值进行相应的操作。
- 该方法使用count变量来记录数组中不重复元素的个数,duplicateCount变量来记录重复元素的个数。
- 遍历数组时,如果当前元素与前一个元素相同,则将duplicateCount加1;否则将count加1。
- 同时,如果duplicateCount大于0,则将当前元素向前移动duplicateCount个位置,相当于删除了重复元素。
- 最后返回count作为新数组的长度。
class Solution {
public int removeDuplicates(int[] nums) {if (nums.length == 0) {return 0;}int count = 1;int duplicateCount = 0;for (int i = 1; i < nums.length; i++) {if (nums[i] == nums[i - 1]) {duplicateCount++;} else {count++;}if (duplicateCount > 0) {nums[i - duplicateCount] = nums[i];}}return count;
}}复杂度分析:
- 时间复杂度:O(n),其中n为数组的长度。需要遍历整个数组一次。
- 空间复杂度:O(1),原地修改数组,不需要额外的空间。
在遍历数组时,只有在出现重复元素时才会对数组进行修改。对数组的修改是通过将重复元素向前移动来实现的,而不是删除重复元素。因此,不需要额外的空间来存储删除后的新数组。这种方法的空间复杂度是常数级别的。
综上所述,使用计数器的解法是一种高效的解决方案,具有线性的时间复杂度和常数级别的空间复杂度。
LeetCode运行结果:
方法四:额外的数组
除了之前提到的思路和方法,还可以使用额外的数组来存储不重复的元素。
该方法创建一个新的数组uniqueNums,用于存储不重复的元素。遍历原始数组时,如果当前元素与前一个元素不相同,则将当前元素添加到uniqueNums数组中,并将计数器count加1。最后,将uniqueNums数组中的元素赋值回原数组nums,并返回count作为新数组的长度。
class Solution {
public int removeDuplicates(int[] nums) {if (nums.length == 0) {return 0;}int[] uniqueNums = new int[nums.length];uniqueNums[0] = nums[0];int count = 1;for (int i = 1; i < nums.length; i++) {if (nums[i] != nums[i - 1]) {uniqueNums[count] = nums[i];count++;}}// 将uniqueNums数组中的元素赋值回原数组for (int i = 0; i < count; i++) {nums[i] = uniqueNums[i];}return count;
}}复杂度分析:
- 时间复杂度:O(n),其中n为数组的长度。需要遍历整个数组一次,并进行一次数组元素的复制操作。
- 空间复杂度:O(n),因为需要使用额外的数组来存储不重复的元素。
在遍历原始数组时,只有在出现与前一个元素不相同的元素时才将其添加到新数组中。因此,新数组的长度最多为原数组的长度,即使用了额外的O(n)空间。
综上所述,使用额外数组的解法是一种线性时间复杂度的解决方案,但需要额外的空间来存储新的数组。这种方法适用于不要求原地修改数组的情况。
LeetCode运行结果:
第三题
题目来源
27. 移除元素 - 力扣(LeetCode)
题目内容


解决方法
方法一:双指针
这道题可以使用双指针的方法来解决。定义两个指针:慢指针slow和快指针fast。
算法的思路如下:
- 初始化慢指针slow为0。
- 遍历数组,如果当前元素nums[fast]等于给定值val,则快指针fast向前移动一步,跳过该元素。
- 如果当前元素nums[fast]不等于给定值val,则将nums[fast]赋值给nums[slow],同时慢指针slow向前移动一步。
- 重复步骤2和步骤3,直到快指针fast遍历完整个数组。
- 返回慢指针slow的值。
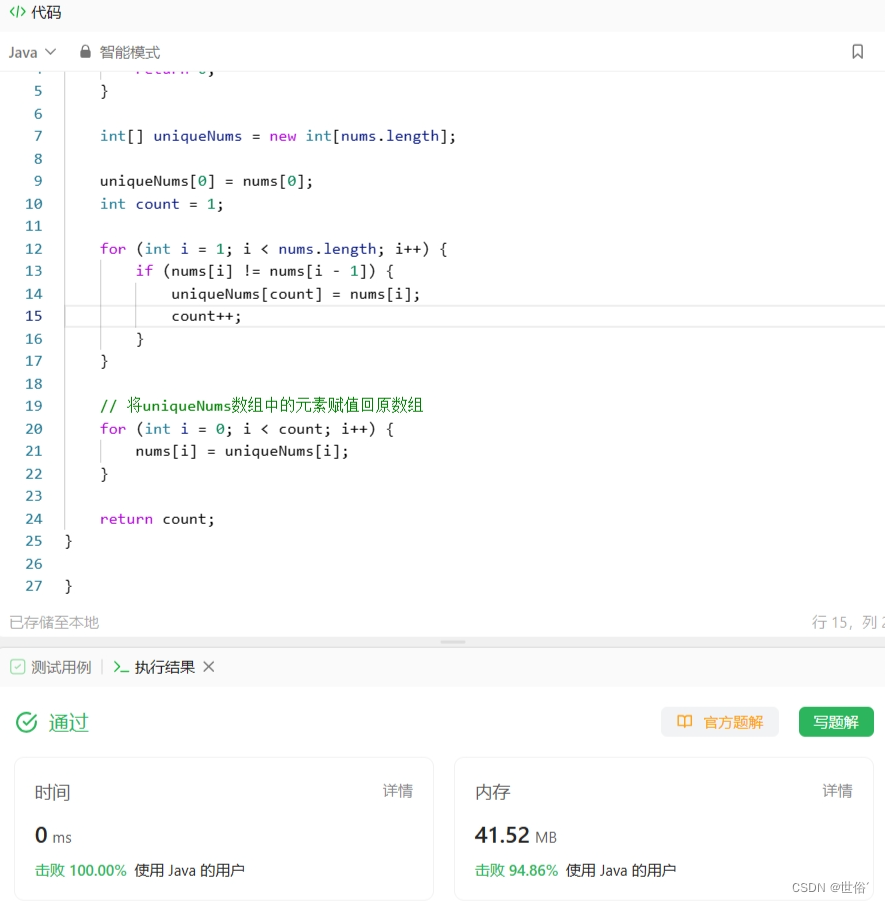
class Solution {
public int removeElement(int[] nums, int val) {int slow = 0;for (int fast = 0; fast < nums.length; fast++) {if (nums[fast] != val) {nums[slow] = nums[fast];slow++;}}return slow;
}}复杂度分析:
- 时间复杂度: 遍历数组所需的时间为 O(n),其中 n 是数组的长度。在每次遍历时,只有快指针需要移动,而慢指针最多移动了 n 次。因此,整个算法的时间复杂度为 O(n)。
- 空间复杂度: 该算法使用了常数个额外变量,不随输入规模 n 变化,因此空间复杂度为 O(1)。无论输入数组的长度如何,算法都只需要固定的额外空间。
综上所述,该算法的时间复杂度为 O(n),空间复杂度为 O(1)。
LeetCode运行结果:
方法二:List
除了双指针的方法,还可以使用 Java 中的 List 来解决这个问题。具体的做法如下:
- 创建一个 List 集合(例如 ArrayList)来存储不等于给定值val的元素。
- 遍历数组,如果当前元素nums[i]不等于给定值val,则将其添加到 List 中。
- 将 List 转换为数组并返回。
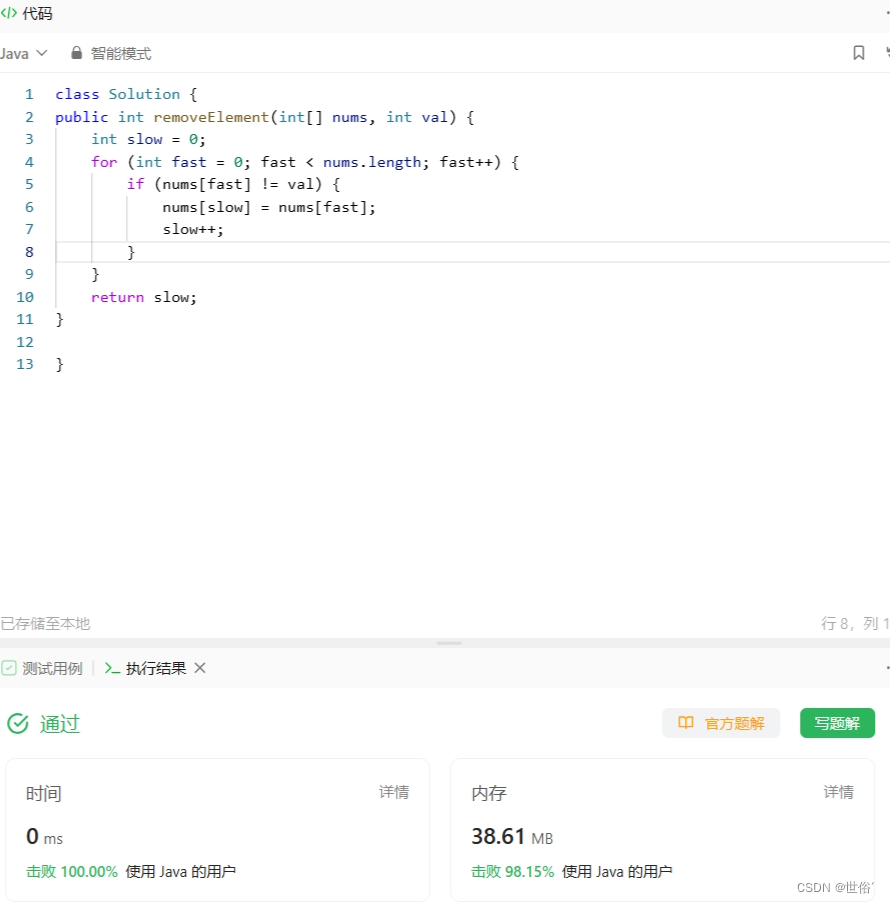
class Solution {
public int removeElement(int[] nums, int val) {List<Integer> list = new ArrayList<>();for (int num : nums) {if (num != val) {list.add(num);}}Integer[] arr = list.toArray(new Integer[list.size()]);for (int i = 0; i < arr.length; i++) {nums[i] = arr[i];}return list.size();
}}这种方法的本质是通过使用 List 集合来存储不等于给定值val的元素,然后将 List 转换为数组并重新赋值给原数组。最后返回 List 的大小即为移除元素后的新长度。
复杂度分析:
时间复杂度:
- 遍历数组并将不等于给定值val的元素添加到 List,时间复杂度为 O(n),其中 n 是数组的长度。
- 将 List 转换为数组,需要遍历 List 中的元素,时间复杂度同样为 O(n)。
综上所述,整个算法的时间复杂度为 O(n)。
空间复杂度:
- 创建了一个大小为 n 的 List 来存储不等于给定值val的元素,占用了额外的 O(n) 空间。
- 将 List 转换为数组时,需要创建一个新的数组,大小为 List 的大小,同样占用了额外的 O(n) 空间。
综上所述,整个算法的空间复杂度为 O(n)。
相比之下,双指针和的方法在空间复杂度上是优于使用 List 的方法的,因为它只需要常数个额外变量,即空间复杂度为 O(1)。因此,建议使用双指针的方法来解决这个问题,以获得更好的空间效率。
LeetCode运行结果:
方法三:交换元素
除了双指针、List,还可以使用交换元素的思路来解决这个问题。具体的做法如下:
- 初始化两个指针i和j,初始值分别为0和数组长度-1。
- 循环移动指针i,直到找到第一个等于给定值val的元素。
- 循环移动指针j,直到找到第一个不等于给定值val的元素。
- 如果i小于j,则将元素nums[j]赋值给nums[i],并将指针i和j分别加1和减1。
- 重复步骤2到步骤4,直到i大于等于j。
- 返回指针i,即为移除元素后的新长度。
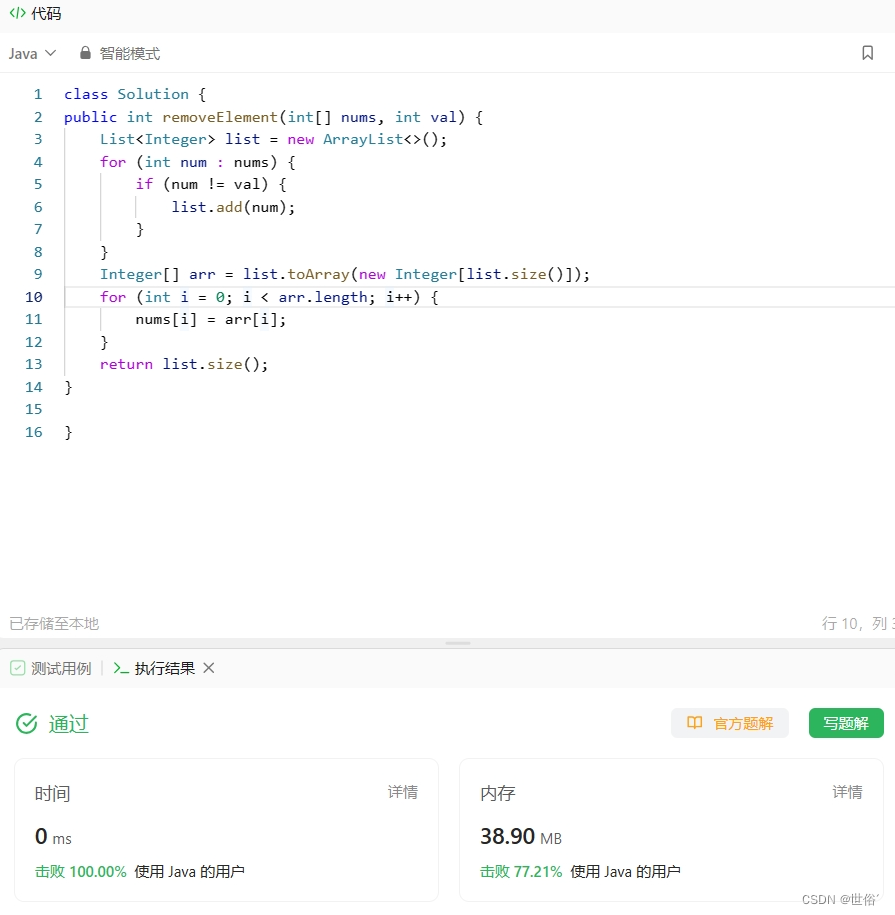
class Solution {
public int removeElement(int[] nums, int val) {int i = 0;int j = nums.length - 1;while (i <= j) {while (i <= j && nums[i] != val) {i++;}while (i <= j && nums[j] == val) {j--;}if (i < j) {nums[i] = nums[j];i++;j--;}}return i;
}}这种交换元素的方法通过使用两个指针分别从头尾向中间移动,并通过交换元素的方式来实现移除元素的目的。
复杂度分析:
- 时间复杂度:使用两个指针分别从头尾向中间移动,最坏情况下需要遍历整个数组,时间复杂度为 O(n),其中 n 是数组的长度。
- 空间复杂度:这种方法只使用常数个额外变量,即空间复杂度为 O(1)。
综上所述,使用交换元素的方法的时间复杂度为 O(n),空间复杂度为 O(1)。与双指针的方法相比,交换元素的方法具有相同的时间复杂度,但空间复杂度更低,因为不需要额外的数据结构(如 List)来存储元素。从空间效率的角度来看,交换元素的方法是较优的选择。
LeetCode运行结果:
方法四:递归
除了双指针、交换元素和使用 List 的方法,还可以利用递归来解决这个问题。具体的做法如下:
- 编写一个递归函数,传入当前遍历到的索引位置和计数器 count。
- 在递归函数中,判断当前遍历到的元素是否等于给定值 val:
- 如果相等,则将计数器 count 加1,并调用递归函数继续处理下一个元素。
- 如果不相等,则将当前元素覆盖掉索引位置 count,并调用递归函数处理下一个元素。
- 递归函数的终止条件是遍历完整个数组,返回计数器 count 的值。
- 在主函数中,调用递归函数,传入初始索引0和计数器初始值0。
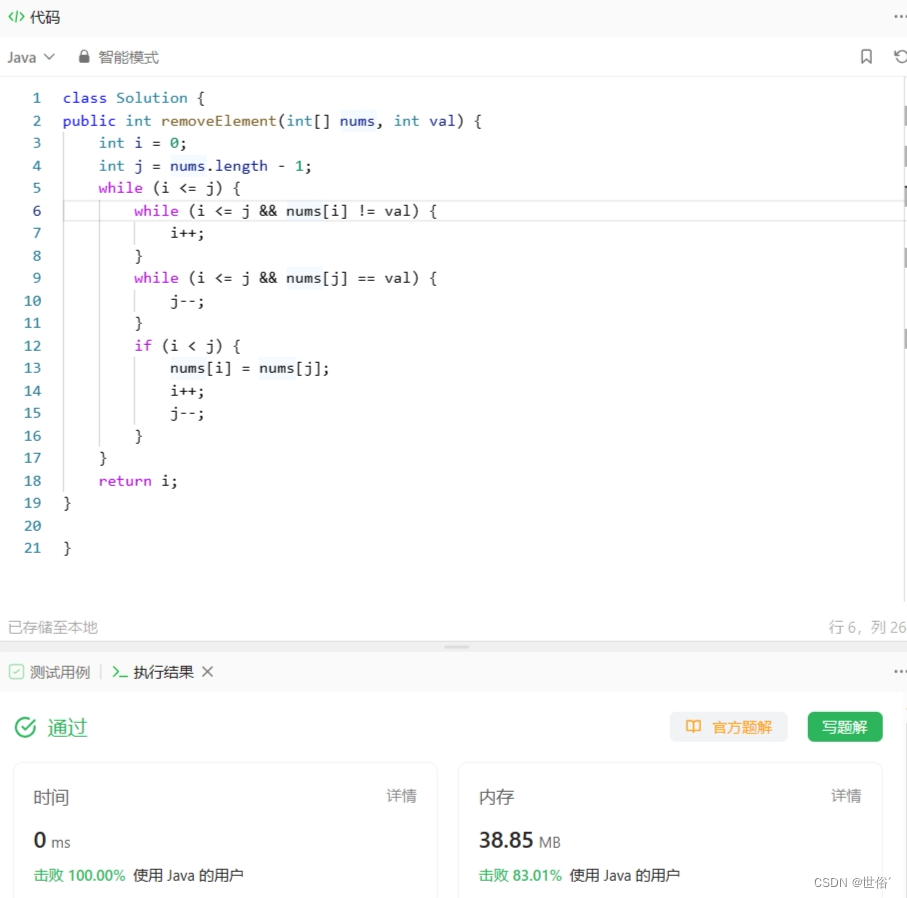
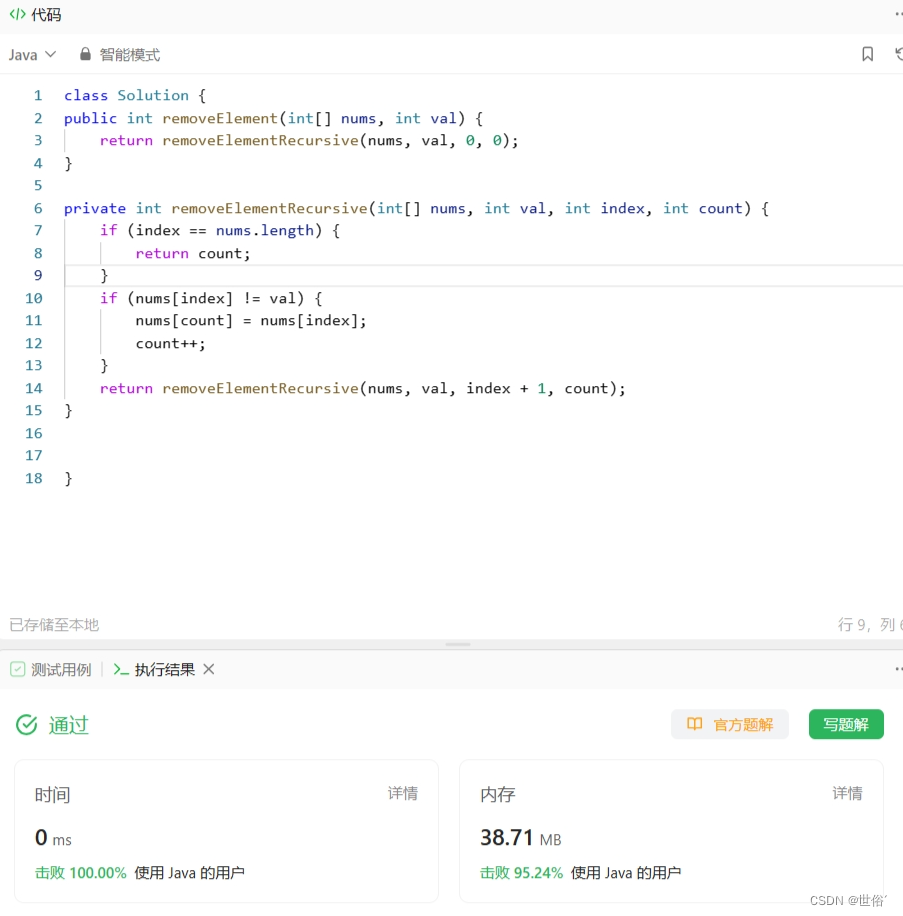
class Solution {
public int removeElement(int[] nums, int val) {return removeElementRecursive(nums, val, 0, 0);
}private int removeElementRecursive(int[] nums, int val, int index, int count) {if (index == nums.length) {return count;}if (nums[index] != val) {nums[count] = nums[index];count++;}return removeElementRecursive(nums, val, index + 1, count);
}}这种递归的方法通过逐个处理数组元素,将不等于给定值 val 的元素覆盖到数组的前部分,从而实现移除元素的目的。
复杂度分析:
- 时间复杂度:递归函数需要遍历整个数组,因此时间复杂度取决于数组的长度,为 O(n),其中 n 是数组的大小。
- 空间复杂度:递归调用会占用一定的栈空间,最坏情况下递归深度为 n,因此空间复杂度为 O(n)。
综上所述,使用递归的方法的时间复杂度为 O(n),空间复杂度为 O(n)。
需要注意的是,递归方法的空间复杂度相对较高,因为每次递归调用都需要在栈上保存一些信息。在处理大规模数组时,可能会导致栈溢出。因此,如果要处理大规模数组,建议使用其他方法,如双指针或交换元素的方法,以保证较低的空间开销。
LeetCode运行结果:
相关文章:

怒刷LeetCode的第11天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:迭代 方法二:递归 方法三:指针转向 第二题 题目来源 题目内容 解决方法 方法一:快慢指针 方法二:Arrays类的sort方法 方法三:计数器 方法四…...

CentOS LVM缩容与扩容步骤
为VM打快照;备份home数据;# yum install xfsdump -y [root@testCentos7 home]# xfsdump -f /dev/home.dump /home xfsdump: using file dump (drive_simple) strategy xfsdump: version 3.1.7 (dump format 3.0) - type ^C for status and control ===================…...

开发者福利!李彦宏将在百度世界大会手把手教你做AI原生应用
目录 一、写在前面 二、大模型社区 2.1 加入频道 2.2 创建应用 一、写在前面 1. “把最先进的技术用到极致,把最先进的应用做到极致。” 2. “每个产品都在热火朝天地重构,不断加深对AI原生应用的理解。” 3. “这就是真正的AI原生应用,这…...
堆的OJ题
🔥🔥 欢迎来到小林的博客!! 🛰️博客主页:✈️林 子 🛰️博客专栏:✈️ 小林的算法笔记 🛰️社区 :✈️ 进步学堂 &am…...

物联网网关:连接设备与云端的桥梁
物联网网关作为连接设备与云端的桥梁,承担着采集数据、设备远程控制、协议转换、数据传输等重要任务。物联网网关是一种网络设备,它可以连接多个物联网设备,实现设备之间的数据传输和通信。物联网网关通常具有较高的网络带宽和处理能力&#…...

ChatGPT企业版来了,速度翻倍,无使用限制
美国时间8月28日,OpenAI宣布了自ChatGPT推出以来最重大的新闻:将推出ChatGPT企业版,企业版ChatGPT将直接对接GPT-4,提供无限制访问、高级数据分析功能、定制服务等服务,并支持处理更长文本输入的长上下文窗口。 OpenAI…...

opencv图像像素类型转换与归一化
文章目录 opencv图像像素类型转换与归一化1、为什么对图像像素类型转换与归一化2、在OpenCV中,convertTo() 和 normalize() 是两个常用的图像处理函数,用于图像像素类型转换和归一化;(1)convertTo() 函数用于将一个 cv…...
【自学开发之旅】Flask-前后端联调-异常标准化返回(六)
注册联调: 前端修改: 1.修改请求向后端的url地址 文件:env.development修改成VITE_API_TARGET_URL http://127.0.0.1:9000/v1 登录:token验证 校验forms/user.py from werkzeug.security import check_password_hash# 登录校验…...
springcloud3 分布式事务解决方案seata之XA模式4
一 seata的模式 1.1 seata的几种模式比较 Seata基于上述架构提供了四种不同的分布式事务解决方案: XA模式:强一致性分阶段事务模式,牺牲了一定的可用性,无业务侵入 TCC模式:最终一致的分阶段事务模式,有…...
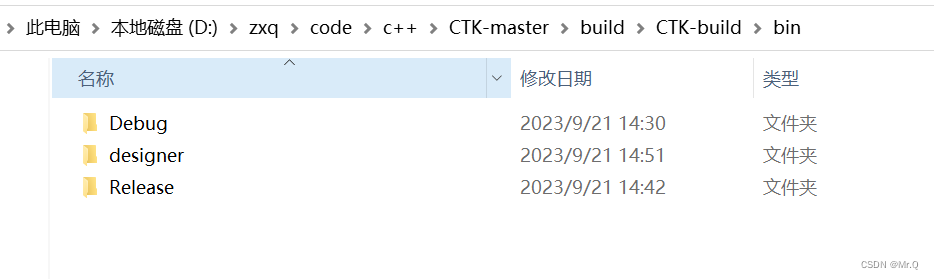
编译ctk源码
目录 前景介绍 下载The Common Toolkit (CTK) cmake-gui编译 vs2019生成 debug版本 release版本 前景介绍 CTK(Common Toolkit)是一个用于医学图像处理和可视化应用程序开发的工具集,具有以下特点: 基于开源和跨平台的Qt框…...
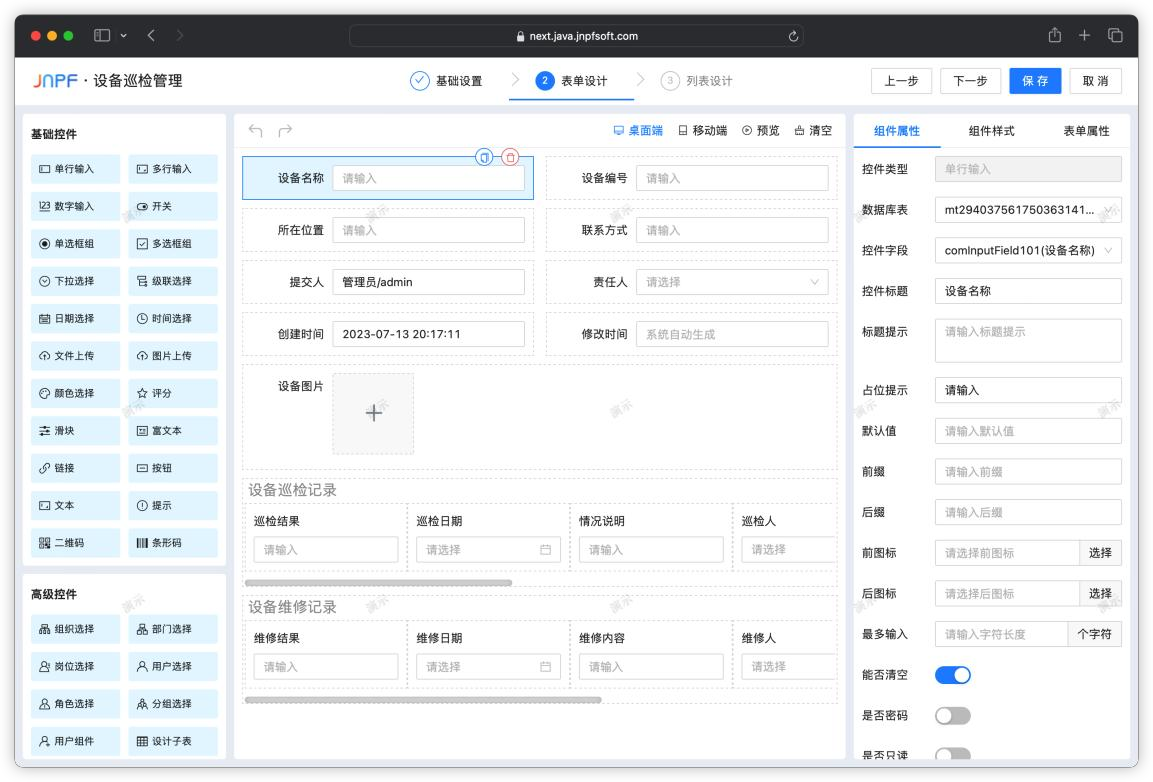
前后端分离的低代码快速开发框架
低代码开发正逐渐成为企业创新的关键工具。通过提高开发效率、降低成本、增强灵活性以及满足不同用户需求,低代码开发使企业能够快速响应市场需求,提供创新解决方案。选择合适的低代码平台,小成本组建一个专属于你的应用。 项目简介 这是一个…...

【Java 基础篇】Java同步代码块解决数据安全
多线程编程是现代应用程序开发中的常见需求,它可以提高程序的性能和响应能力。然而,多线程编程也带来了一个严重的问题:数据安全。在多线程环境下,多个线程同时访问和修改共享的数据可能导致数据不一致或损坏。为了解决这个问题&a…...

亿纬锦能项目总结
项目名称:亿纬锦能 项目链接:https://www.evebattery.com 项目概况: 此项目用到了 wow.js/slick.js/swiper-bundle.min.js/animate.js/appear.js/fullpage.js以及 slick.css/animate.css/fullpage.css/swiper-bundle.min.css/viewer.css 本项目是一种…...
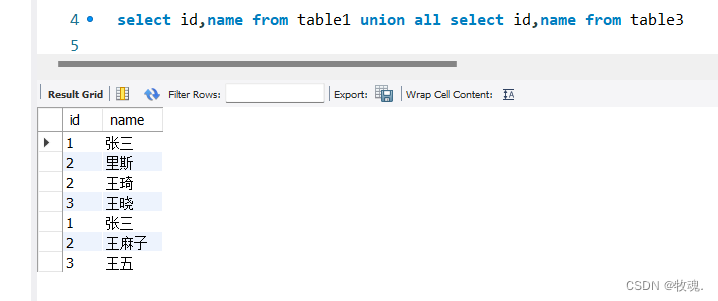
简明 SQL 组合查询指南:掌握 UNION 实现数据筛选
在SQL中,组合查询是一种将多个SELECT查询结果合并的操作,通常使用UNION和UNION ALL两种方式。 UNION 用于合并多个查询结果集,同时去除重复的行,即只保留一份相同的数据。UNION ALL 也用于合并多个查询结果集,但不去除…...

【springMvc】自定义注解的使用方式
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《Spring与Mybatis集成整合》 ⛺️ 生活的理想,为了不断更新自己 ! 1.前言 1.1.什么是注解 Annontation是Java5开始引入的新特征,中文名称叫注解。 它提供了一种安全…...
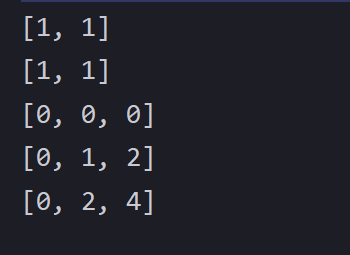
求二维子数组的和(剖析)
文章目录 🐒个人主页🏅JavaSE系列专栏📖前言:本篇剖析一下二维子数组求和规则: 🐒个人主页 🏅JavaSE系列专栏 📖前言:本篇剖析一下二维子数组求和 规则: 这…...
代码开发思路介绍)
无(低)代码开发思路介绍
无代码或者低代码开发的思路,是通过非编程代码,而是基于页面拖拉拽的方式来实现创建web应用的功能。 作为程序员我们知道私有云公有云已经实现了基础设施的web方式管理。DEVOPS把代码发布,管理也实现了web方式管理。那么我们很容易能够想到,只要把拖拉拽出来的项目自动化部…...

代码随想录刷题 Day14
144.二叉树的前序遍历(opens new window) 要注意下创建函数参数传递不是很理解 class Solution { public:void tranversal(TreeNode* s, vector<int> &b) {if (s NULL) {return;}b.push_back(s->val);tranversal(s->left, b);tranversal(s->right, b);}v…...

二分类问题的解决利器:逻辑回归算法详解(一)
文章目录 🍋引言🍋逻辑回归的原理🍋逻辑回归的应用场景🍋逻辑回归的实现 🍋引言 逻辑回归是机器学习领域中一种重要的分类算法,它常用于解决二分类问题。无论是垃圾邮件过滤、疾病诊断还是客户流失预测&…...

docker alpine镜像中遇到 not found
1.问题: docker alpine镜像中遇到 sh: xxx: not found 例如 # monerod //注:此可执行文件已放到/usr/local/bin/ sh: monerod: not found2.原因 由于alpine镜像使用的是musl libc而不是gnu libc,/lib64/ 是不存在的。但他们是兼容的&…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...

视觉slam--框架
视觉里程计的框架 传感器 VO--front end VO的缺点 后端--back end 后端对什么数据进行优化 利用什么数据进行优化的 后端是怎么进行优化的 回环检测 建图 建图是指构建地图的过程。 构建的地图是点云地图还是什么信息的地图? 建图并没有一个固定的形式和算法…...
