【数据结构】图的应用:最小生成树;最短路径;有向无环图描述表达式;拓扑排序;逆拓扑排序;关键路径
目录
1、最小生成树
1.1 概念
1.2 普利姆算法(Prim)
1.3 克鲁斯卡尔算法(Kruskal)
2、最短路径
2.1 迪杰斯特拉算法(Dijkstra)
2.2 弗洛伊德算法(Floyd)
2.3 BFS算法,Dijkstra算法,Floyd算法的对比
3、有向无环图描述表达式
3.1 有向无环图定义及特点
3.2 描述表达式
4、拓扑排序
4.1 AOV网
4.2 步骤
4.3 DFS实现拓扑排序
5、逆拓扑排序
5.1 步骤
5.2 DFS实现逆拓扑排序
6、关键路径
6.1 AOE网
6.2 求解方法
6.3 特性
1、最小生成树
1.1 概念
最小生成树是一种基于图的算法,用于在一个连通加权无向图中找到一棵生成树,使得树上所有边的权重之和最小。最小生成树指一张无向图的生成树中边权最小的那棵树。生成树是指一张无向图的一棵极小连通子图,它包含了原图的所有顶点,但只有足以构成一棵树的 n-1 条边。最小生成树可以用来解决最小通信代价、最小电缆费用、最小公路建设等问题。常见的求解最小生成树的算法有Prim算法和Kruskal算法。

1.2 普利姆算法(Prim)
Prim算法的基本思想是从一个任意顶点开始,每次添加一个距离该顶点最近的未访问过的顶点和与之相连的边,直到所有顶点都被访问过。
其基本步骤如下:
-
初始化:定义一个空的集合S表示已经确定为最小生成树的结点集合,和一个数组dist表示当前结点到S集合中最短距离,初始时S集合为空,数组dist中所有元素为正无穷,将任意一个结点u加到S集合中。
-
找到到S集合距离最近的结点v,并将v加入到S集合中。
-
更新数组dist,更新S集合中的结点到其它结点的距离。对于所有不在S集合中的结点w,如果从v到w的距离小于dist[w],则更新dist[w]的值为从v到w的距离。
-
重复以上步骤2和步骤3,直到所有的结点都加入到S集合中,即构成了最小生成树。
该算法的时间复杂度为O(n^2),其中n为图的顶点数。
以下是用C语言实现Prim算法的代码,假设图的节点从0到n-1编号。
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>#define MAX_N 1000 // 最大顶点数
#define INF INT_MAX // 正无穷
#define false 0
#define true 1// 无向图的邻接矩阵表示法
int graph[MAX_N][MAX_N]; // 图的邻接矩阵
int visited[MAX_N]; // 标记结点是否已加入最小生成树
int dist[MAX_N]; // 记录结点到最小生成树的距离
int parent[MAX_N]; // 记录结点的父节点(即最小生成树的边)int prim(int n)
{// 初始化for (int i = 0; i < n; i++) {visited[i] = false;dist[i] = INF;parent[i] = -1;}dist[0] = 0; // 从结点0开始构建最小生成树for (int i = 0; i < n - 1; i++) { // n - 1次循环int min_dist = INF;int min_index = -1;// 找出距离最小生成树最近的结点for (int j = 0; j < n; j++) {if (!visited[j] && dist[j] < min_dist) {min_dist = dist[j];min_index = j;}}if (min_index == -1) {break; // 找不到未访问的结点,算法结束}visited[min_index] = true;// 更新未加入最小生成树的结点到最小生成树的距离和父节点for (int j = 0; j < n; j++) {if (!visited[j] && graph[min_index][j] < dist[j]) {dist[j] = graph[min_index][j];parent[j] = min_index;}}}// 输出最小生成树int cost = 0;for (int i = 1; i < n; i++) {printf("%d -> %d : %d\n", parent[i], i, graph[i][parent[i]]);cost += graph[i][parent[i]];}return cost;
}int main()
{int n; // 结点数量int m; // 边数量scanf("%d%d", &n, &m);// 初始化邻接矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {graph[i][j] = INF;}}// 读入边for (int i = 0; i < m; i++) {int u, v, w;scanf("%d%d%d", &u, &v, &w);graph[u][v] = w;graph[v][u] = w; // 无向图,所以要加上反向边}int cost = prim(n);printf("cost = %d\n", cost);return 0;
}dist数组记录的是结点到最小生成树的距离,parent数组记录的是结点的父节点,visited数组记录结点是否已加入最小生成树。在每次循环中,找出距离最小生成树最近的结点,并将其标记为已访问,再更新未加入最小生成树的结点到最小生成树的距离和父节点。最后输出最小生成树的边,以及最小生成树的总权值(即边的权值之和)。
1.3 克鲁斯卡尔算法(Kruskal)
Kruskal算法的基本思想是先将图中所有边按边权从小到大排序,然后逐个加入到生成树中,但是要保证加入后生成树仍然是无环的。如果加入某一条边形成了环,则不加入该边,继续考虑下一条边。
步骤如下:
- 将所有边按照边权从小到大排序;
- 初始化一个空的树;
- 从排序后的边列表中选择权重最小的边,并判断这条边的两个端点是否在同一棵树中;
- 如果这条边的两个端点不在同一棵树中,则将这条边加入最小生成树中,并将这两个端点所在的树合并成一棵树;
- 重复步骤3和步骤4,直到所有的边都被考虑过。
以下是用C语言实现Kruskal算法的代码,假设图的节点从0到n-1编号。
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>#define MAX_N 1000 // 最大顶点数
#define INF INT_MAX // 正无穷
#define false 0
#define true 1// 边的结构体
typedef struct Edge {int u;int v;int w;
} Edge;Edge edges[MAX_N * MAX_N]; // 边集合
int parent[MAX_N]; // 记录结点的父节点
int rank[MAX_N]; // 记录结点所在集合的秩int cmp(const void* a, const void* b)
{Edge* edge1 = (Edge*)a;Edge* edge2 = (Edge*)b;return edge1->w - edge2->w;
}int find(int x)
{// 路径压缩if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];
}void unite(int x, int y)
{// 按秩合并int root_x = find(x);int root_y = find(y);if (rank[root_x] < rank[root_y]) {parent[root_x] = root_y;} else {parent[root_y] = root_x;if (rank[root_x] == rank[root_y]) {rank[root_x]++;}}
}int kruskal(int n, int m)
{// 初始化for (int i = 0; i < n; i++) {parent[i] = i;rank[i] = 0;}// 按边权从小到大排序qsort(edges, m, sizeof(Edge), cmp);// 构建最小生成树int cost = 0;int count = 0;for (int i = 0; i < m; i++) {int u = edges[i].u;int v = edges[i].v;int w = edges[i].w;if (find(u) != find(v)) { // 判断是否在同一个集合中unite(u, v);cost += w;count++;if (count == n - 1) { // 边数等于n-1,生成树构建完成break;}}}// 输出最小生成树边for (int i = 0; i < n; i++) {if (parent[i] == i) { // 找到根节点for (int j = 0; j < m; j++) {if ((edges[j].u == i && parent[edges[j].v] == i)|| (edges[j].v == i && parent[edges[j].u] == i)) {printf("%d -> %d : %d\n", edges[j].u, edges[j].v, edges[j].w);}}}}return cost;
}int main()
{int n; // 结点数量int m; // 边数量scanf("%d%d", &n, &m);// 读入边并构建边集合for (int i = 0; i < m; i++) {int u, v, w;scanf("%d%d%d", &u, &v, &w);edges[i].u = u;edges[i].v = v;edges[i].w = w;}int cost = kruskal(n, m);printf("cost = %d\n", cost);return 0;
}其中,边的结构体包括起点、终点和边权。在Kruskal算法中,先对边按照权值从小到大进行排序,每次取出最小的边,如果它不连通任何已经选出的边,则加入最小生成树中。为了判断两个结点是否在同一个集合中,可以使用并查集的数据结构,其中parent数组记录结点的父节点,rank数组记录结点所在集合的秩。并查集的find和unite函数实现路径压缩和按秩合并。最后输出最小生成树的边,以及最小生成树的总权值(即边的权值之和)。
2、最短路径
2.1 迪杰斯特拉算法(Dijkstra)
Dijkstra算法是一种解决单源最短路径问题的贪心算法,它的基本思路是从起点开始,每次选择当前最短路径中的一个顶点,然后更新它的邻居的最短路径。
以下是Dijkstra算法的详细步骤:
-
初始化数据结构:创建一个距离数组dist,用来记录起点到每个顶点的最短距离,初始化为正无穷;创建一个visited数组,记录每个顶点是否被访问过;创建一个前驱数组path,记录每个顶点的前驱顶点。
-
将起点的dist设为0,将visited设为false,将path设为null。
-
对于起点的所有邻居,更新它们的dist为起点到邻居的距离,并将它们的path设为起点。
-
重复以下步骤,直到所有顶点都被访问过: a. 从未被访问过的顶点中,选择dist最小的顶点作为当前顶点。 b. 将当前顶点设为已访问。 c. 对当前顶点的所有邻居,如果当前顶点到邻居的距离比邻居的dist值小,就更新邻居的dist值和path值。
-
通过prev数组可找到从起点到任意顶点的最短路径。
下面是一个使用C语言实现Dijkstra算法的示例:
#include <stdio.h>
#include <limits.h>#define V 6 // 顶点数// 寻找dist数组中最小值对应的下标
int minDistance(int dist[], bool visited[])
{int min = INT_MAX, min_index;for (int v = 0; v < V; v++)if (visited[v] == false && dist[v] <= min)min = dist[v], min_index = v;return min_index;
}// 打印最短路径
void printPath(int path[], int dest)
{if (path[dest] == -1)return;printPath(path, path[dest]);printf("%d ", dest);
}// 打印最短路径和距离
void printSolution(int dist[], int path[], int src)
{printf("Vertex\tDistance\tPath");for (int i = 0; i < V; i++){printf("\n%d -> %d\t%d\t\t%d ", src, i, dist[i], src);printPath(path, i);}
}// Dijkstra算法
void dijkstra(int graph[V][V], int src)
{int dist[V]; // 存储src到各个顶点的最短距离bool visited[V]; // 标记顶点是否已访问过int path[V]; // 存储最短路径// 初始化for (int i = 0; i < V; i++)dist[i] = INT_MAX, visited[i] = false, path[i] = -1;dist[src] = 0;// 计算最短路径for (int count = 0; count < V - 1; count++){int u = minDistance(dist, visited);visited[u] = true;for (int v = 0; v < V; v++)if (!visited[v] && graph[u][v] && dist[u] != INT_MAX && dist[u] + graph[u][v] < dist[v])dist[v] = dist[u] + graph[u][v], path[v] = u;}// 打印结果printSolution(dist, path, src);
}int main()
{// 构建邻接矩阵int graph[V][V] = {{0, 4, 0, 0, 0, 0},{4, 0, 8, 0, 0, 0},{0, 8, 0, 7, 0, 4},{0, 0, 7, 0, 9, 14},{0, 0, 0, 9, 0, 10},{0, 0, 4, 14, 10, 0}};dijkstra(graph, 0); // 计算从0开始的最短路径return 0;
}在上述代码中,我们使用邻接矩阵来表示图,使用dist数组来记录起点到各个顶点的最短距离,使用visited数组来记录顶点是否已访问过,使用path数组来记录最短路径。
2.2 弗洛伊德算法(Floyd)
Floyd算法是一种动态规划算法,用于解决有向图中任意两点之间的最短路径问题。 时间复杂度为O(n^3),其中n为节点数。其步骤如下:
1. 创建一个n × n的矩阵D来表示任意两点之间的最短距离,其中n为图的顶点数。
2. 初始化矩阵D,对于每个顶点i,设其到自身的距离为0,对于所有i和j之间存在边的情况,设其距离为对应的边权值,如果不存在边,则将对应的D[i][j]设为无穷大。
3. 对于任意的k∈[1,n],依次考虑顶点1~n,并计算经过顶点k的最短路径,即计算D[i][j] = min(D[i][j], D[i][k] + D[k][j]),其中i,j∈[1,n]。
4. 经过第3步的计算后,矩阵D中存储的即为任意两点之间的最短距离。
5. 如果矩阵D中存在负环,说明存在一些顶点之间的距离可以无限缩小,此时无法得到正确的最短路径。
6. 如果需要求出最短路径,则需要借助于一个前驱矩阵P,其中P[i][j]表示从i到j的最短路径上,j的前驱顶点是哪个。可以通过在计算D[i][j]时,将P[i][j]设置为经过的顶点k,来得到前驱矩阵P。
下面是C语言实现Floyd算法的示例代码:
#include <stdio.h>
#include <limits.h>#define INF INT_MAX
#define MAXN 100int dist[MAXN][MAXN];
int path[MAXN][MAXN];void floyd(int n) {/* 初始化距离矩阵和路径矩阵 */for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (i == j) {dist[i][j] = 0;path[i][j] = -1; /* 表示 i 到 j 没有中间节点 */} else {dist[i][j] = INF;path[i][j] = -1;}}}/* 根据边权值更新距离矩阵和路径矩阵 */int u, v, w;while (scanf("%d %d %d", &u, &v, &w) == 3) {dist[u][v] = w;path[u][v] = u; /* i 到 j 的路径经过 u */}/* 计算任意两点之间的最短路径 */for (int k = 0; k < n; k++) {for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (dist[i][k] < INF && dist[k][j] < INF && dist[i][j] > dist[i][k] + dist[k][j]) {dist[i][j] = dist[i][k] + dist[k][j];path[i][j] = path[k][j]; /* i 到 j 的路径经过 u 的话,i 到 k 的路径就经过 u 了,于是将 i 到 k 的路径经过的节点挂到 i 到 j 的路径上 */}}}}
}void print_path(int u, int v) {if (path[u][v] == -1) { /* i 到 j 没有中间节点 */printf("%d", v);} else { /* i 到 j 的路径经过 u */print_path(u, path[u][v]); /* 递归打印 i 到 u 的路径 */printf("->%d", v);}
}int main() {int n;scanf("%d", &n);floyd(n);int s, t;scanf("%d %d", &s, &t);printf("%d\n", dist[s][t]);print_path(s, t);return 0;
}该代码首先读入图的规模 n,然后读入每条边的起点、终点和边权值,根据这些信息构建邻接矩阵。然后,它使用Floyd算法计算任意两点之间的最短路径和路径矩阵。最后,给定起点 s 和终点 t,输出它们之间的最短路程和路径。
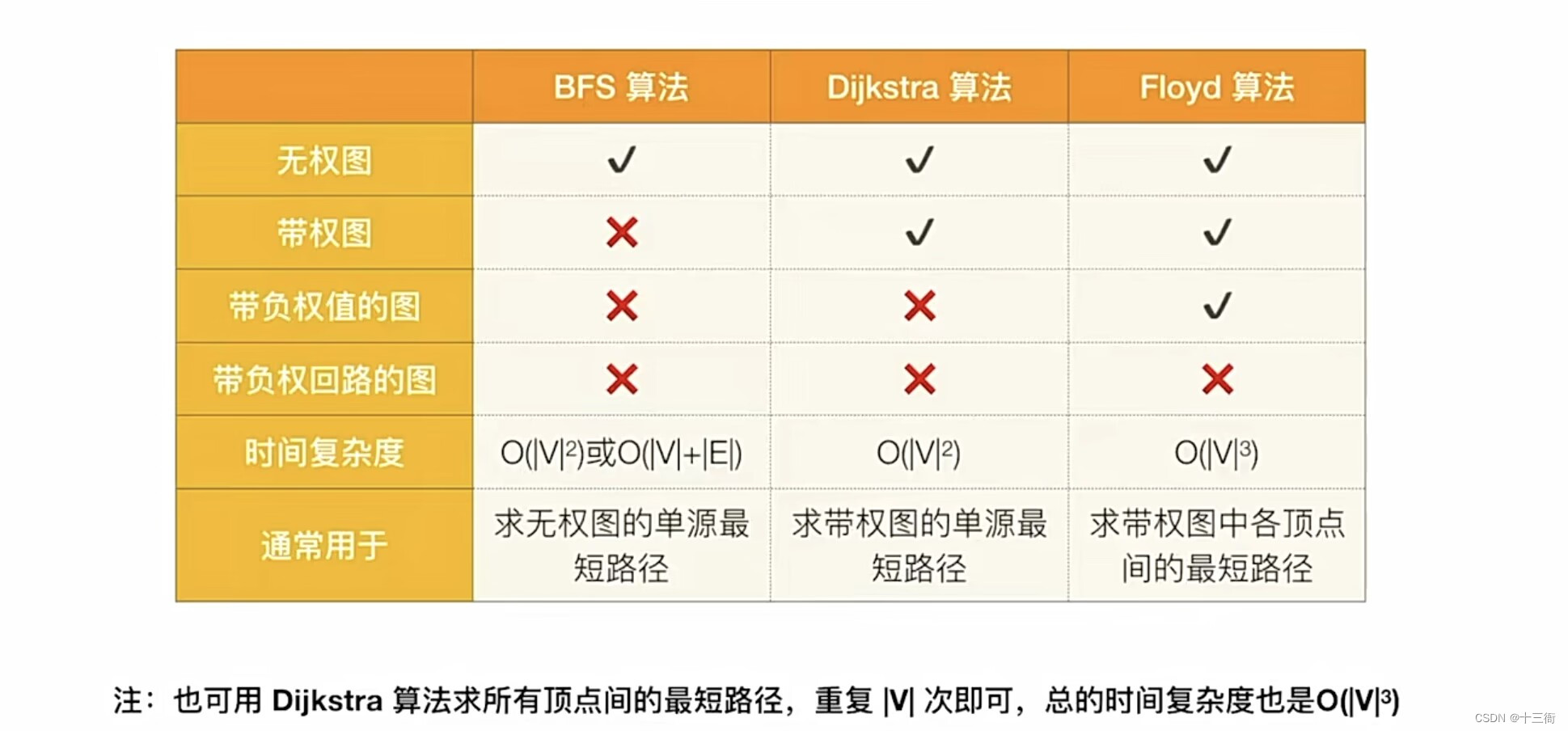
2.3 BFS算法,Dijkstra算法,Floyd算法的对比
3、有向无环图描述表达式
3.1 有向无环图定义及特点
有向无环图(Directed Acyclic Graph,简称DAG)是一种有向图,其中不存在环路,即从任意一个顶点出发不可能经过若干条边回到此顶点。通常用来表示任务调度、依赖关系等场景,具有以下特点:
1. 有向性:DAG中所有边均有方向,即起点指向终点。
2. 无环性:DAG中不存在环路,即不能从一个顶点出发沿其周游返回此顶点。
3. 顶点与边的关系:DAG中的顶点表示任务、事件、状态等,边表示依赖关系、控制关系等。
4. 拓扑排序:DAG可以进行拓扑排序,即将DAG中所有顶点排序,使得对于任意一条边(u,v),顶点u都排在v的前面。
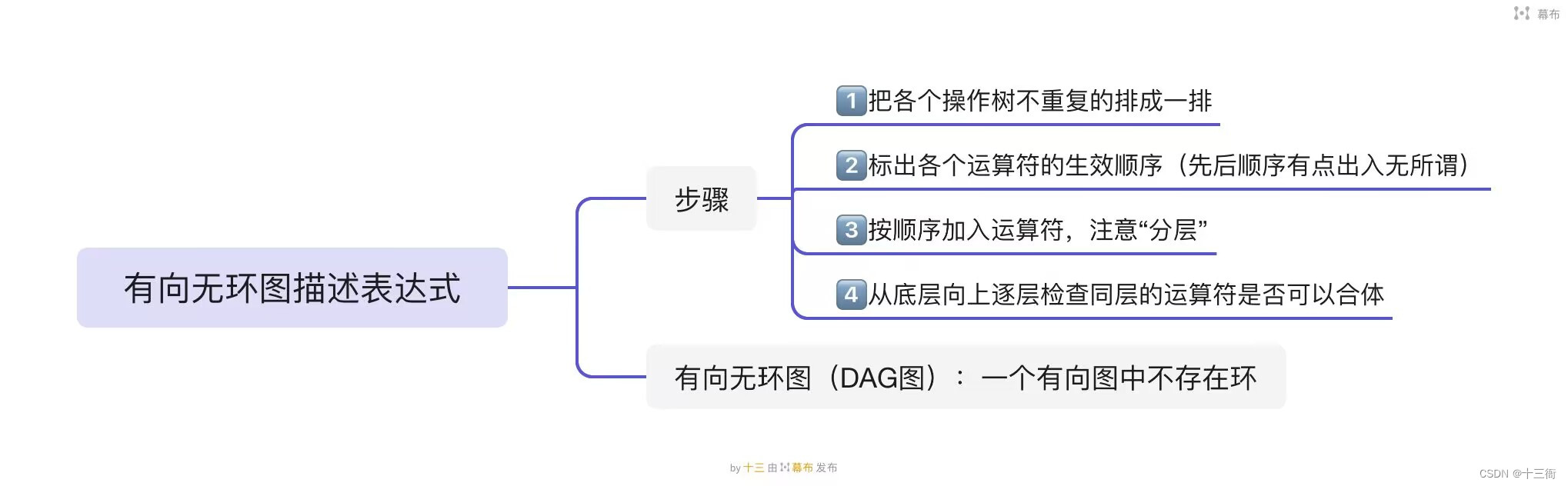
3.2 描述表达式
有向无环图可以用于描述表达式的计算顺序,其中每个节点表示一个操作符或操作数,每个有向边表示操作数或操作符之间的依赖关系和计算顺序。
例如,对于表达式 "5*(2+3)":
首先,将 "+" 表示为一个节点,并有两个入边和一条出边; 然后,将 "2" 和 "3" 也表示为节点,并分别与 "+" 节点相连; 接着,再将 "*" 表示为节点,并与 "5" 和 "+" 节点相连; 最后,整个有向无环图如图所示:
+ // "+" 节点/ \/ \2 3 // "2" 和 "3" 节点\ /\ /* // "*" 节点|5 // "5" 节点
按照拓扑排序的顺序遍历这个有向无环图,就可以得到表达式的计算顺序:2 -> 3 -> + -> 5 -> *,即先计算 2 和 3 的和,再将结果与 5 相乘,最后得到结果 25。
4、拓扑排序
4.1 AOV网

4.2 步骤
拓扑排序是对有向图进行排序的一种算法,步骤如下:
1. 初始化:首先,将所有入度为0的顶点加入到一个队列中。
2. 遍历:从队列中取出一个顶点,输出该顶点并删除该顶点的所有出边(即将它所指向的顶点的入度减1)。如果该顶点删除后所指向的结点入度为0,则将其加入队列中。
3. 重复遍历:重复以上操作,直到队列为空为止。
4. 判断:如果输出的顶点数等于图中的顶点数,则拓扑排序成功,并输出结果;否则,图中存在环,拓扑排序失败。

4.3 DFS实现拓扑排序
DFS实现拓扑排序的基本思路是:从任意一个没有后继节点的节点出发,沿着它的各个链路不断深入,并记录经过的节点,直到到达一个没有出边的节点为止。在返回的过程中,将经过的节点依次加入结果数组中,直到所有的节点都加入到结果数组中。
DFS实现拓扑排序的C语言代码示例:
#include <stdio.h>
#include <stdlib.h>
#define MAXN 1000int n, m;
int G[MAXN][MAXN]; //邻接矩阵存图
int vis[MAXN], res[MAXN], idx = 0; //vis数组用于记录是否访问过,res数组用于存储结果void dfs(int u){vis[u] = 1; //标记为已访问for(int v = 0; v < n; v++){if(G[u][v] && !vis[v]){ //如果v是u的后继节点且未被访问过dfs(v); //继续深入}}res[idx++] = u; //将该节点存入结果数组中
}void topSort(){for(int i = 0; i < n; i++){if(!vis[i]){ //从未被访问过的节点出发dfs(i);}}for(int i = n - 1; i >= 0; i--){ //倒序输出结果数组printf("%d ", res[i]);}
}int main(){scanf("%d%d", &n, &m);for(int i = 0; i < m; i++){int u, v;scanf("%d%d", &u, &v);G[u][v] = 1; //有向边}topSort();return 0;
}其中,G数组为邻接矩阵存储图,vis数组用于记录是否访问过,res数组用于存储结果,idx为结果数组的下标。topSort函数是主要的拓扑排序算法,遍历所有节点并调用dfs函数,dfs函数通过递归的方式实现深度优先遍历。最后,倒序输出结果数组,即可得到拓扑排序的结果。
5、逆拓扑排序
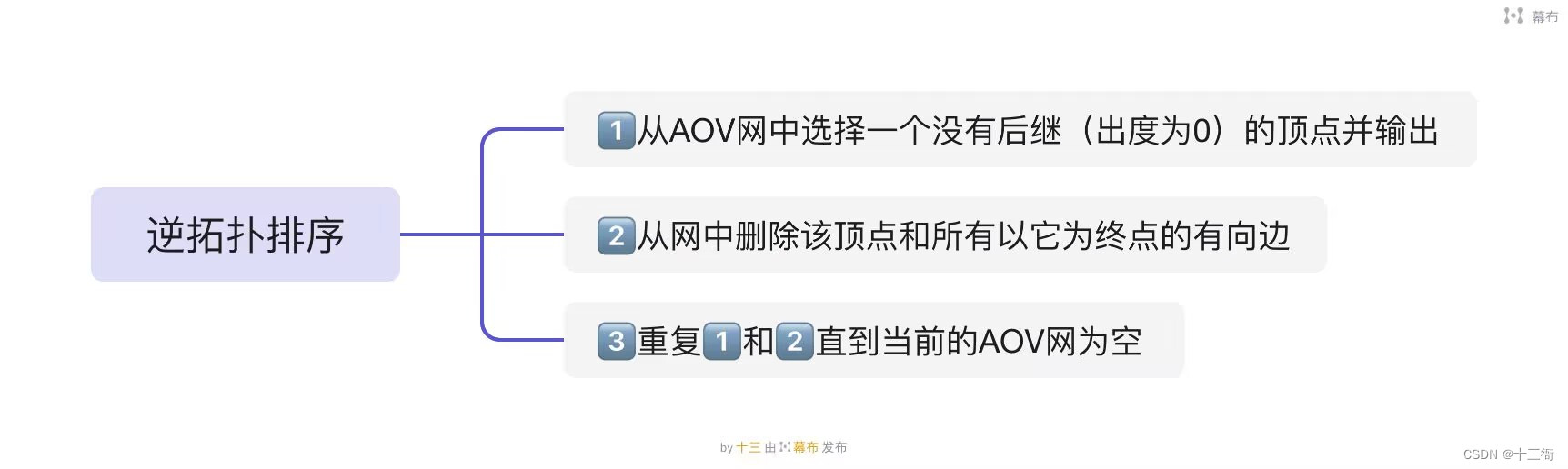
5.1 步骤
逆拓扑排序是指在一个有向无环图中,对于每个节点v,输出所有能够到达v的节点。逆拓扑排序的步骤如下:
1. 初始化一个空的结果列表和一个空的队列。
2. 对于每个节点v,计算能够到达v的节点数目,记为out_degree[v]。
3. 将所有out_degree[v]为0(出度为0)的节点加入队列。
4. 当队列非空时,取出队首节点u,并将其加入结果列表。
5. 对于u的每个邻居节点v,将out_degree[v]减1。
6. 若out_degree[v]等于0,则将v加入队列。
7. 重复步骤4-6直到队列为空。
8. 返回结果列表。
5.2 DFS实现逆拓扑排序
逆拓扑排序指的是在一个有向无环图(DAG)中,对所有节点进行排序,使得对于任意一条有向边(u, v),都有排在前面的节点先于排在后面的节点。逆拓扑排序可以通过深度优先搜索(DFS)实现。具体实现步骤如下:
-
定义一个数组visited,用于记录每个节点是否已经被访问过,初始值为0。
-
定义一个栈stack,用于存储已经访问过的节点。
-
对于每个节点u,进行DFS搜索,具体步骤如下:
a. 标记节点u已经被访问过,visited[u]=1。
b. 对于节点u的每个邻接节点v,如果该节点还没有被访问过,则进行DFS搜索。
c. 将节点u入栈。
-
当所有节点都搜索完毕后,从栈顶开始按顺序取出节点,生成逆拓扑排序结果。
下面是C语言实现代码:
#include <stdio.h>
#define MAX_VERTEX_NUM 100int visited[MAX_VERTEX_NUM], topo[MAX_VERTEX_NUM], top = -1;
int vex_num, arc_num;
int Graph[MAX_VERTEX_NUM][MAX_VERTEX_NUM];void DFS(int u) {visited[u] = 1;int v;for (v = 0; v < vex_num; v++) {if (Graph[u][v] == 1 && visited[v] == 0) {DFS(v);}}topo[++top] = u;
}void TopoSort() {int i, j;for (i = 0; i < vex_num; i++) {visited[i] = 0;}top = -1;for (i = 0; i < vex_num; i++) {if (visited[i] == 0) {DFS(i);}}printf("逆拓扑排序结果:");for (i = vex_num - 1; i >= 0; i--) {printf("%d ", topo[i]);}
}int main() {int i, j, u, v;scanf("%d%d", &vex_num, &arc_num);for (i = 0; i < vex_num; i++) {for (j = 0; j < vex_num; j++) {Graph[i][j] = 0;}}for (i = 0; i < arc_num; i++) {scanf("%d%d", &u, &v);Graph[u][v] = 1;}TopoSort();return 0;
}
示例输入:
7 10
0 1
0 2
1 3
1 5
1 4
2 5
3 6
4 6
5 4
5 6
示例输出:
逆拓扑排序结果:0 2 1 5 4 3 6
6、关键路径
6.1 AOE网

6.2 求解方法
关键路径是某个项目中的最长路径,它决定了整个项目的总时长,需要正确地计算和管理。以下是关键路径的求解方法:
1. 确定项目的活动和它们的先后关系。
2. 绘制网络图,包括活动的节点和它们之间的连接线,确定每个活动的预计持续时间和最早开始时间。
3. 根据网络图计算每个活动的最早开始时间和最迟开始时间。
4. 计算每个活动的最早完成时间和最迟完成时间。
5. 通过计算每个活动的浮动时间,确定哪些活动是关键路径上的活动。
6. 将关键路径上的活动按照其完成时间的顺序排列,找出整个项目的最长时间和关键路径。
7. 对于非关键路径上的活动,可以进行资源优化,以缩短项目的总时长。
总之,关键路径的求解需要清晰的项目规划和正确的计算方法,能够帮助项目管理人员更好地控制项目进度和资源,确保项目按时完成。

6.3 特性

博主正在学习中,如果博文中有解释错误的内容,请大家指出
🤞❤️🤞❤️🤞❤️图的应用的知识点总结就到这里啦,如果对博文还满意的话,劳烦各位大佬儿动动“发财的小手”留下您对博文的赞和对博主的关注吧🤞❤️🤞❤️🤞❤️

相关文章:

【数据结构】图的应用:最小生成树;最短路径;有向无环图描述表达式;拓扑排序;逆拓扑排序;关键路径
目录 1、最小生成树 1.1 概念 1.2 普利姆算法(Prim) 1.3 克鲁斯卡尔算法(Kruskal) 2、最短路径 2.1 迪杰斯特拉算法(Dijkstra) 2.2 弗洛伊德算法(Floyd) 2.3 BFS算法&…...

大数据驱动业务增长:数据分析和洞察力的新纪元
文章目录 大数据的崛起大数据的特点大数据技术 大数据驱动业务增长1. 洞察力和决策支持2. 个性化营销3. 风险管理4. 产品创新 大数据分析的新纪元1. 云计算和大数据示例代码:使用AWS的Elastic MapReduce(EMR)进行大数据分析。 2. 人工智能和机…...

科技云报道:分布式存储红海中,看天翼云HBlock如何突围?
科技云报道原创。 过去十年,随着技术的颠覆性创新和新应用场景的大量涌现,企业IT架构出现了稳态和敏态的混合化趋势。 在持续产生海量数据的同时,这些新应用、新场景在基础设施层也普遍基于敏态的分布式架构构建,从而对存储技术…...
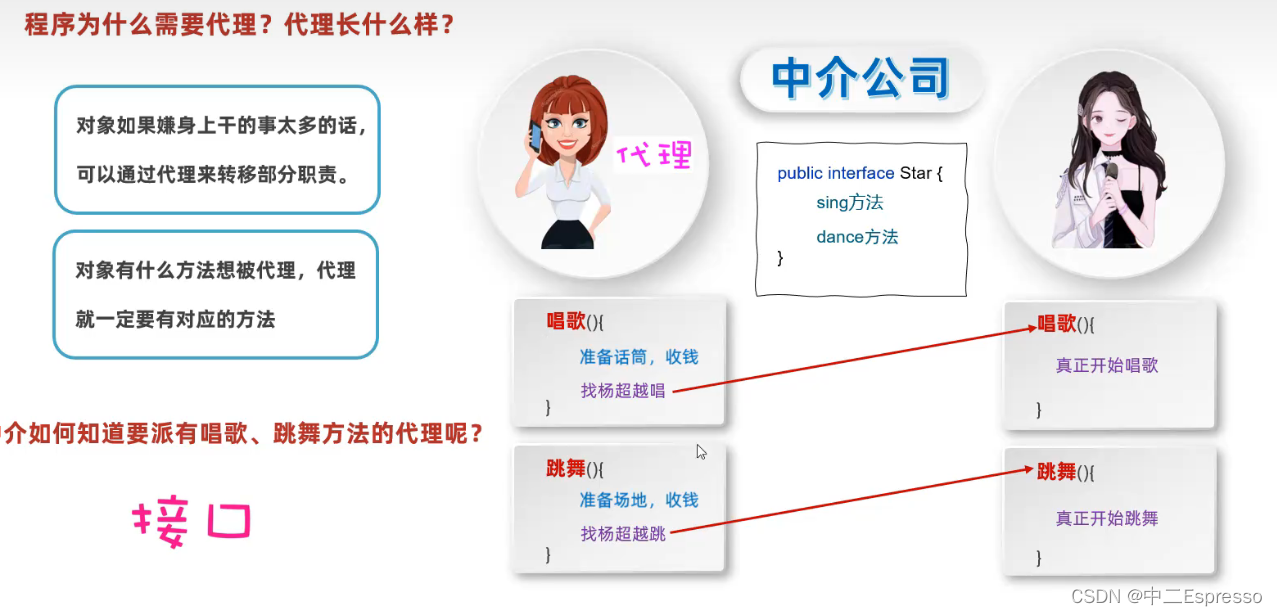
Java高级-动态代理
动态代理 1.介绍2.案例 1.介绍 public interface Star {String sing(String name);void dance(); }public class BigStar implements Star{private String name;public BigStar(String name) {this.name name;}public String sing(String name) {System.out.println(this.name…...

时序预测 | MATLAB实现POA-CNN-LSTM鹈鹕算法优化卷积长短期记忆神经网络时间序列预测
时序预测 | MATLAB实现POA-CNN-LSTM鹈鹕算法优化卷积长短期记忆神经网络时间序列预测 目录 时序预测 | MATLAB实现POA-CNN-LSTM鹈鹕算法优化卷积长短期记忆神经网络时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现POA-CNN-LSTM鹈鹕算法优化卷积长短…...

n个不同元素进栈,求出栈元素的【不同排列】以及【排列的数量】?
我在网上看的博客大部分是告诉你这是卡特兰数,然后只给出了如何求解有多少种排列,没有给出具体排列是怎么样的。如果你还不知道卡特兰数,请查看:https://leetcode.cn/circle/discuss/lWYCzv/ 这里记录一下如何生成每种具体的排列…...

Python中TensorFlow的长短期记忆神经网络(LSTM)、指数移动平均法预测股票市场和可视化...
原文链接:http://tecdat.cn/?p23689 本文探索Python中的长短期记忆(LSTM)网络,以及如何使用它们来进行股市预测(点击文末“阅读原文”获取完整代码数据)。 相关视频 在本文中,你将看到如何使用…...

多线程的学习第二篇
多线程 线程是为了解决并发编程引入的机制. 线程相比于进程来说,更轻量 ~~ 更轻量的体现: 创建线程比创建进程,开销更小销毁线程比销毁进程,开销更小调度线程比调度进程,开销更小 进程是包含线程的. 同一个进程里的若干线程之间,共享着内存资源和文件描述符表 每个线程被独…...
git之撤销工作区的修改和版本回溯
有时候在工作区做了一些修改和代码调试不想要了,可如下做 (1)步骤1:删除目录代码,确保.git目录不能修改 (2)git log 得到相关的commit sha值 可配合git reflog 得到相要的sha值 (3)执行git reset --hard sha值,可以得到时间轴任意版本的代码 git reset --hard sha值干净的代…...

sed awk使用简介
简介 本文主要介绍 Linux 系统的两个神级工具:sed 和 awk ,他们是Linux高手们必备的技能,很值得我们去研究的东西。 这里是我在网上书上收集的相关资料,因为这两个工具很有名也很重要,所以这些资料会帮助我更好的了解…...
竞赛选题 基于深度学习的人脸识别系统
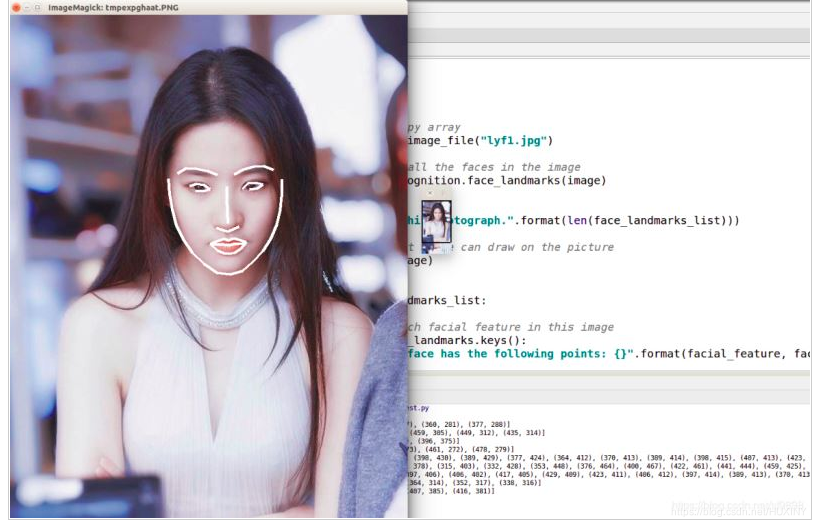
前言 🔥 优质竞赛项目系列,今天要分享的是 基于深度学习的人脸识别系统 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🧿 更多资料, 项目分享: https://gitee.com/dancheng-senior/…...

idea Terminal 回退历史版本 Git指令 git reset
——————强制回滚历史版本—————— 一、idea Terminal 第一步:复制版本号 (右击项目–> Git --> Show History -->选中要回退的版本–>Copy Revision Number,直接复制;) 第二步:ide…...
华为云云耀云服务器L实例评测|华为云上安装监控服务Prometheus三件套安装
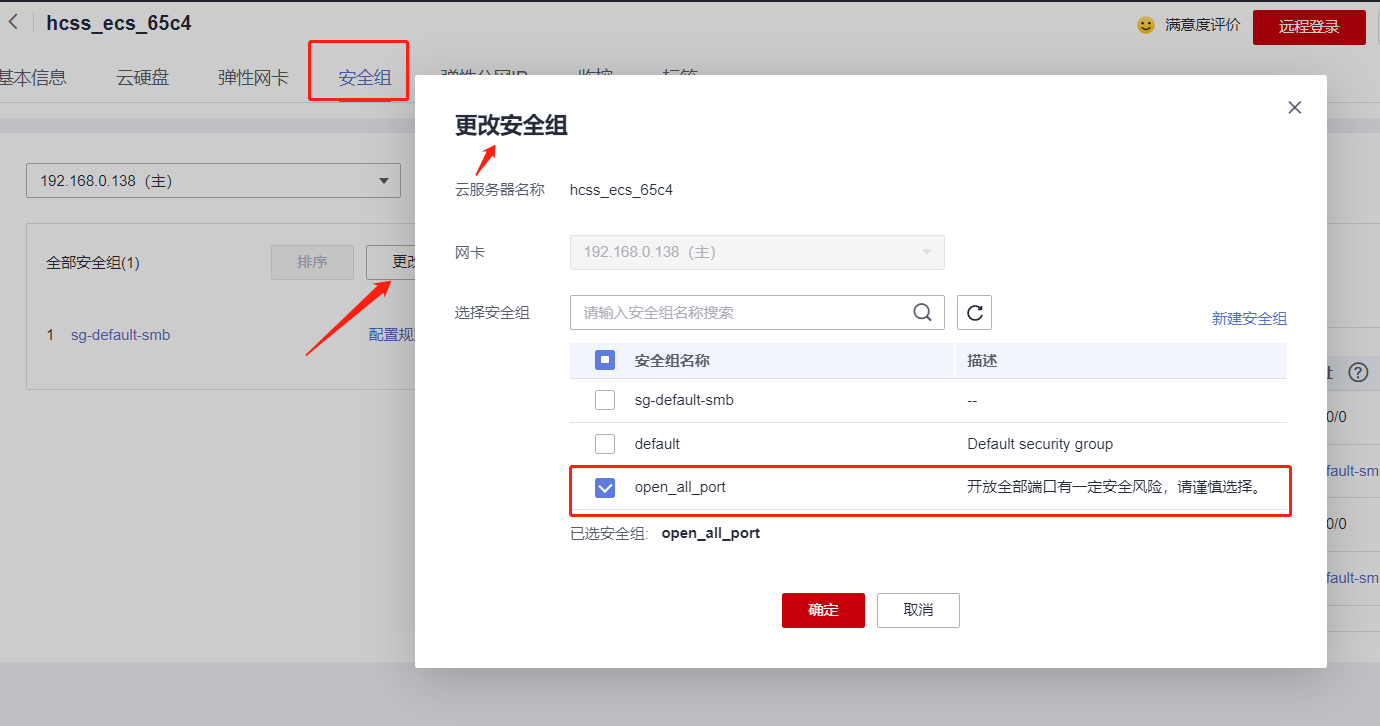
文章目录 华为云云耀云服务器L实例评测|华为云上试用监控服务Prometheus一、监控服务Prometheus三件套介绍二、华为云主机准备三、Prometheus安装四、Grafana安装五、alertmanager安装六、三个服务的启停管理1. Prometheus、Alertmanager 和 Grafana 启动顺序2. 使用…...

C语言基础知识点(八)联合体和大小端模式
以下程序的输出是() union myun {struct { int x, y, z;} u;int k; } a; int main() {a.u.x 4;a.u.y 5;a.u.z 6;a.k 0;printf("%d\n", a.u.x); } 小端模式 数据的低位放在低地址空间,数据的高位放在高地址空间 简记ÿ…...

一个线程运行时发生异常会怎样?
如果一个线程在运行时发生异常而没有被捕获(即未被适当的异常处理代码处理),则会导致以下几种情况之一: 线程终止:线程会立即终止其执行,并将异常信息打印到标准错误输出(System.err)。这通常包括异常的类型、堆栈跟踪信息以及异常消息。 ThreadDeath 异常:在某些情况…...

CSS中去掉li前面的圆点方法
1. 引言 在网页开发中,我们经常会使用无序列表(<ul>)来展示一系列的项目。默认情况下,每个列表项(<li>)前面都会有一个圆点作为标记。然而,在某些情况下,我们可能希望去…...

Python:获取当前目录下所有文件夹名称及文件夹下所有文件名称
获取当前目录下所有文件夹名称 def get_group_list(folder_path):group_list []for root, dirs, files in os.walk(folder_path):for dir in dirs:group_list.append(dir)return group_list获取文件夹下所有文件名称 def get_file_list(folder_path, group_name):file_list …...
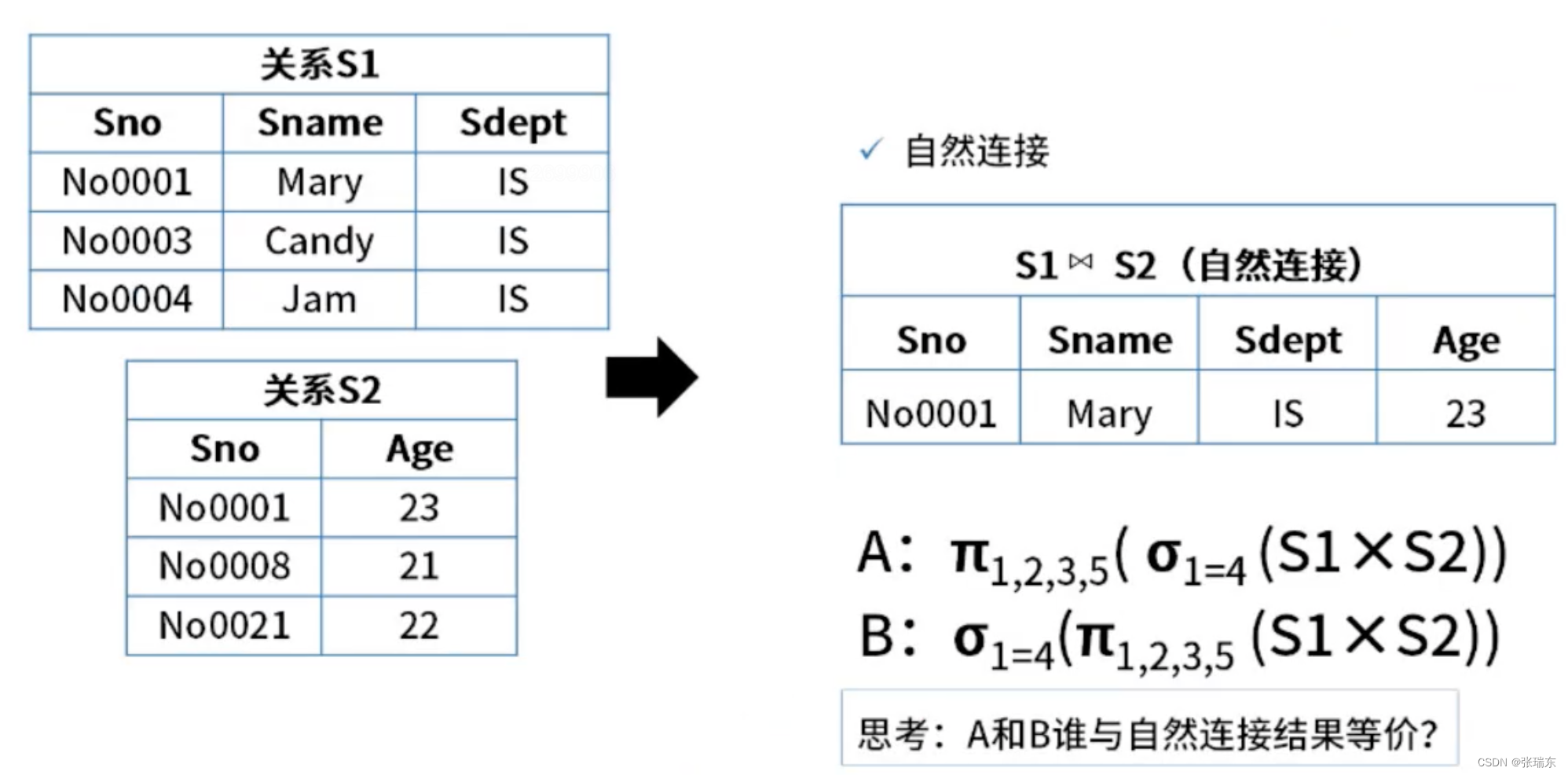
系统架构设计师-数据库系统(1)
目录 一、数据库模式 1、集中式数据库 2、分布式数据库 二、数据库设计过程 1、E-R模型 2、概念结构设计 3、逻辑结构设计 三、关系代数 1、并交差 2、投影和选择 3、笛卡尔积 4、自然连接 一、数据库模式 1、集中式数据库 三级模式: (1)外…...

Docker的相关知识介绍以及mac环境的安装
一、什么是Docker 大型项目组件较多,运行环境也较为复杂,部署时会碰到一些问题: 依赖关系复杂,容易出现兼容性问题开发、测试、生产环境有差异 Docker就是来解决这些问题的。Docker是一个快速交付应用、运行应用的技术&#x…...
Android设计支持库
本文所有的代码均存于 https://github.com/MADMAX110/BitsandPizzas 设计支持库(Design Support Library)是 Google 在 2015 年的 I/O 大会上发布的全新 Material Design 支持库,在这个 support 库里面主要包含了 8 个新的 Material Design …...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...
