2023华为杯研究生数学建模C题分析
完整的分析查看文末名片获取!
问题一 在每个评审阶段,作品通常都是随机分发的,每份作品需要多位评委独立评审。为了增加不同评审专家所给成绩之间的可比性,不同专家评审的作品集合之间应有一些交集。但有的交集大了,则必然有交集小了,则可比性变弱。请针对3000支参赛队和125位评审专家,每份作品由5位专家评审的情况,建立数学模型确定最优的“交叉分发”方案,并讨论该方案的有关指标(自己定义)和实施细节。
问题一主要是需要为3000支参赛队和125位评审专家建立一个最优的“交叉分发”方案。这里的关键是要保证每份作品由5位专家评审,并且不同专家评审的作品集合之间有一定的交集。这个问题可以看作是一个组合优化问题,我们可以使用图论模型,将其建模为图的顶点着色问题,并求解得到最优的“交叉分发”方案。
我们的变量为,定义二进制变量xij,当第i位专家评审第j份作品时为1,否则为0。
我们的目标函数是要最大化所有专家之间作品交集的大小,即最大化
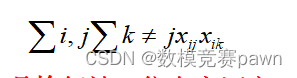
我们给定约束条件,每份作品恰好被5位专家评审;每位专家评审的作品数量应均匀分布,防止某位专家评审任务过重或过轻。
这是一个NP-hard问题,我们可以应用遗传算法、模拟退火算法等启发式算法进行求解。这些算法适用于搜索大规模组合优化问题的解空间,能够在合理时间内找到满意解。
问题二 在评审中采用标准分(附件1)为基础的排序方法,其假设是不同评审专家评审的作品集合的学术水平分布相同。但在大规模创新类竞赛评审中,通常任意两位专家评审的作品只有小部分是共同的,绝大多数作品是不同的(见问题一),而且每位专家只看到作品集合的很小部分,因此标准分评审方案的假设可能不成立,需要探索新的评审方案。请选择两种或两种以上现有或自己设计的评审方案和题目附件数据,分析每位专家、每份作品原始成绩、调整之后(如取标准分)成绩的分布特点,按不同方案进行排序,并设法比较这些方案的优劣。进而针对大规模创新类竞赛的评审,设计新的标准分(公式)计算模型。另外,一般认为经多位专家协商一致的获奖论文具有最大的可信度,附件2提供的数据1,其第二评审阶段评选出的一等奖作品排序是经专家协商取得一致的,请利用这批数据,改进你们的标准分计算模型。
问题二涉及到对不同的评审方案进行比较和分析,以及基于给定的数据设计新的标准分计算模型。我们可以对现有的几种评审方案进行分析,利用描述性统计学和假设检验等方法来比较这些方案的优劣。,如均值、中位数、标准差等,来分析每位专家、每份作品原始成绩和调整后成绩的分布特点。对不同方案下的成绩分布我们做一些可视化的展示,来更直观地了解不同方案之间的差异。
为了判断不同方案之间的差异是否显著,我们可以使用假设检验方法。通过ANOVA(方差分析)来比较多个方案下成绩的均值是否存在显著差异。使用卡方检验或Fisher精确检验来比较不同方案下成绩的分布差异。
然后基于这些分析结果,设计新的标准分计算模型,这个问题可以考虑使用回归分析,除了使用回归分析,我们还可以构建一个优化模型来求解最优的标准分计算方法。这个模型的目标函数可以是最小化所有作品标准分的方差,以减少不同方案之间的差异。约束条件可以包括保持评分的公平性、保持一定的差异性。
问题三 “创新类”大赛的特点是“创新性”,即没有标准答案。由于这类竞赛的问题难度较大,一般需要通过创新才能在竞赛期间部分解决。而作品的创新到了什么程度,后续研究的前景如何,很难有一致看法,即使专家面对面的交流,都可能由于各持己见而无法统一。加上研究生的论文表达不到位,评审专家的视角不同,同一份作品的几位专家给出的成绩会有较大的差异(极差)。极差大是大规模创新类竞赛的特点,极差比较大的作品一般处于高分段或低分段。低分段属于淘汰范围,低分段极差大的原因是有专家对违规作品或有重大失误的作品给了很低的分数,或评审专家都认同该作品质量不高,只是其中某位(些)专家更不认同该作品。故这里极差虽大,但属于不获奖范畴,一般不需要调整极差。而高分段作品还要参加权威性较高的第二阶段评审(附件数据表格同一行代表同一个作品在两个阶段的成绩,没有第二阶段评审成绩的作品只参加了第一阶段的评审)。第二阶段评审仍然存在部分极差大的作品,因为是终审,误差可能影响获奖等级,因此对部分极差大的作品,需要复议调整极差(附件的数据中有记录,复议分就是该专家最后给的标准分,用来替换原来的标准分)。第二阶段(注意两个阶段每份作品评审专家人数不同)专家调整“大极差”的规律可以作为建立极差模型的借鉴。
请根据题目所给的模拟数据2.1和2.2,讨论两阶段的成绩整体的变化和两阶段极差整体的变化,分析两阶段评审方案相比不分阶段评审方案的优劣。注意到极差大和创新性强两大特点之间会有一定的关系,为了发掘创新论文,请建立“极差”模型(含分析、分类、调整等),并针对所给数据,尝试给出第一评审阶段程序化(不需要人工干预)处理非高且非低分段作品的 “大极差”的办法。
问题三我们要聚焦于两阶段评审方案与不分阶段评审方案的比较,以及“极差”模型的建立。需要去分析两阶段的成绩变化、极差变化,并探讨如何处理“大极差”。
比较两阶段评审方案和不分阶段评审方案,可以通过方差分析(ANOVA)来比较两阶段评审方案和不分阶段评审方案的成绩差异,检验不同方案下成绩的均值是否有显著差异,以及这些差异是否可以归因于使用的评审方案
然后去计算它们的均值、标准差、四分位数差等描述性统计量,可以更详细地了解两种方案在成绩分布上的差异。以及通过可视化工具如箱线图、直方图等可以去展现这些差异。
建立极差模型的话,用分类和聚类都可以,先是分类模型,我们来来预测作品的极差大小。通过输入作品的各种特征(如各位专家的初步评分、作品类型等),分类模型可以预测该作品的极差是否会超过某个阈值。算法的话,可以用决策树、随机森林、支持向量机等。最后通过交叉验证来选择最佳的模型和参数。
聚类分析的话,我们可以将具有相似极差特性的作品分为同一类。可以让我们了解哪些作品更容易产生大的极差,聚类算法可以用K-means聚类或者层次聚类。
问题四 对“创新类”竞赛,给出一个完整的评审模型(提示:例如优化模型),并针对所给的数据研究如何求解?也可对现行的评审方案给出改进的具体建议(包括未来还要收集哪些数据)。
更多的思路代码↓↓
相关文章:
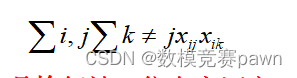
2023华为杯研究生数学建模C题分析
完整的分析查看文末名片获取! 问题一 在每个评审阶段,作品通常都是随机分发的,每份作品需要多位评委独立评审。为了增加不同评审专家所给成绩之间的可比性,不同专家评审的作品集合之间应有一些交集。但有的交集大了,则…...
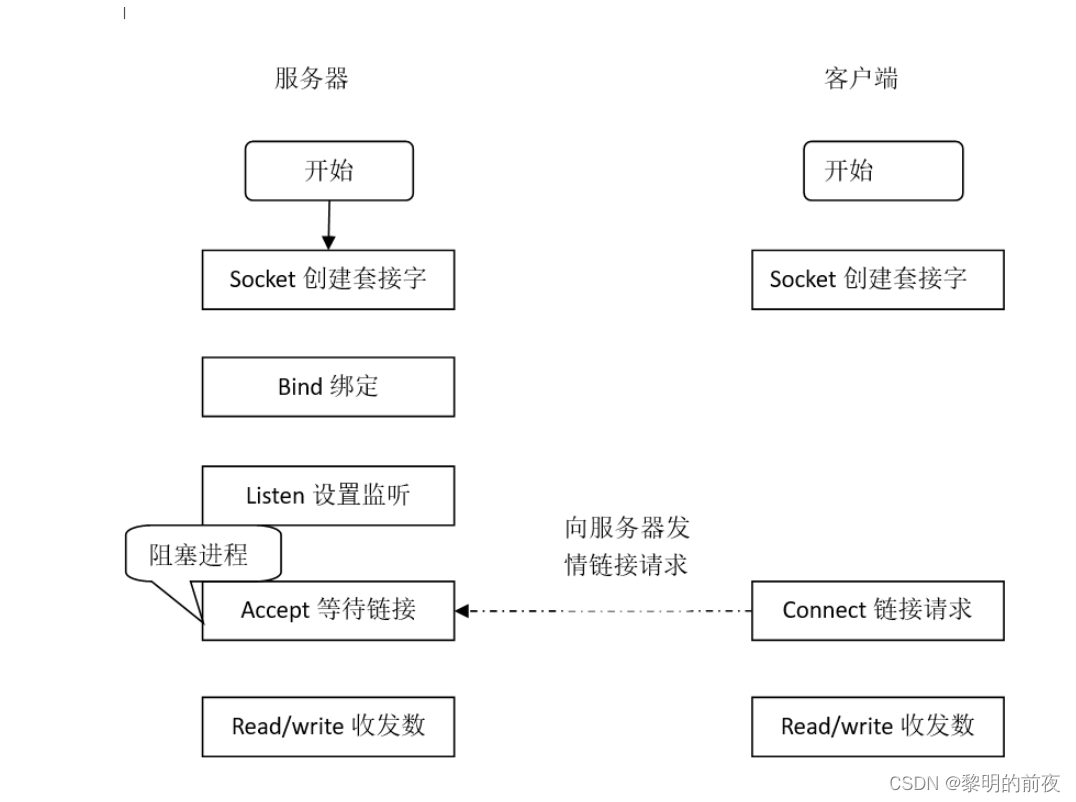
第三天:实现网络编程基于tcp/udp协议在Ubuntu与gec6818开发板之间双向通信
互联网地址 每一台设备接入互联网后,都会举报一个唯一的地址编号 IP地址 INTERNET地址 internet地址 :它是协议上的一个逻辑地址 目前来说,我们主要的IP地址有两类 IPV4 IPV6 IPV4 其实就是使用一个32bit整数作为IP IPV6 其实就是使用一…...
Transport)
【MediaSoup---源码篇】(三)Transport
概述 RTC::Transport是mediasoup中的一个重要概念,它用于在mediasoup与客户端之间传输实时音视频数据。 Transport继承着众多的类,主要用于Transport的整体感知 class Transport : public RTC::Producer::Listener,public RTC::Consumer::Listener,publ…...

爱分析《商业智能最佳实践案例》
近日,国内知名数字化市场研究咨询机构爱分析发布《2023爱分析商业智能最佳实践案例》,此评选活动面向落地商业智能的各行企业和商业智能厂商,以第三方专业视角深入调研,评选出具有参考价值的创新案例。永达汽车集团与数聚股份合作…...

golang:context
context作用 goroutine的退出机制 多个goroutine都是平行的被调度的,多个goroutine如何协调工作涉及通信、同步、通知和退出 通信:goroutine之间的通信同步chan通道 同步:不带缓冲的chan提供了一个天然的同步等待机制。通过WaitGroup也可以…...

探讨代理IP与Socks5代理在跨界电商中的网络安全应用
在数字化时代,跨界电商已经成为了商业世界中的一大趋势。然而,跨越国界的电商活动也伴随着网络安全挑战。本文将讨论如何利用代理IP和Socks5代理技术来提高跨界电商中的网络安全,同时也探讨了与游戏相关的爬虫应用。 1. 代理IP和Socks5代理的…...
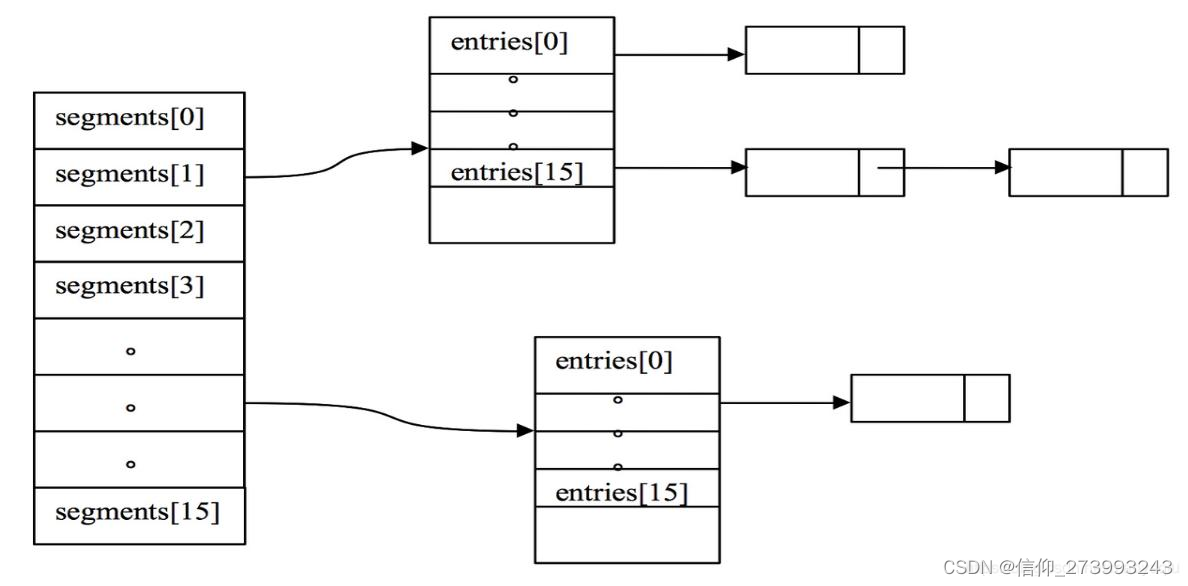
Guava Cache介绍-面试用
一、Guava Cache简介 1、简介 Guava Cache是本地缓存,数据读写都在一个进程内,相对于分布式缓存redis,不需要网络传输的过程,访问速度很快,同时也受到 JVM 内存的制约,无法在数据量较多的场景下使用。 基…...

ARM 汇编指令作业(求公约数、for循环实现1-100之间和、从SVC模式切换到user模式简单写法)
1、求两个数最大公约数 .text .globl _start_start:mov r0, #9mov r1, #15 Loop: 循环cmp r0,r1 比较r0和r1的大小beq stop 当r0和r1相等时,跳到stop标签subhi r0,r0,r1 r0-r1>0 时,证明r0>r1,将r0-r1的值赋给r0&…...

Go - 【字符串,数组,哈希表】常用操作
一. 字符串 字符串长度: s : "hello" l : len(s) fmt.Println(l) // 输出 5遍历字符串: s : "hello" for i, c : range s {fmt.Printf("%d:%c ", i, c) } // 输出:0:h 1:e 2:l 3:l 4:ofor i : 0; i < le…...

vue 普通组件的 局部注册
vue 普通组件的 注册 11 Vue2_3入门到实战-配套资料\01-随堂代码素材\day03\素材\00-准备代码\小兔鲜首页静态页\src...
医疗虚拟仿真和虚拟现实有什么区别?哪个更好?
随着我们在仿真教育中越来越多地使用新技术,区分虚拟模式的类型很重要。虚拟仿真是一个统称,用来概括术语来描述各种基于仿真的体验,从基于屏幕的平台到沉浸式虚拟现实。然而,各虚拟平台在保真度、沉浸感和临场感的水平上有很大差…...

【.net core】yisha框架使用nginx代理swagger接口无法访问问题
后端代码配置 #在StartUp.cs文件中Configure方法中增加以下代码 app.UseSwagger(c >{//代理路径访问c.PreSerializeFilters.Add((doc, item) >{//根据代理服务器提供的协议、地址和路由,生成api文档服务地址doc.Servers new List<OpenApiServer>{ new…...

uniapp录音功能和音频播放功能制作
录音功能 在 UniApp 中,你可以使用 uni.getRecorderManager() 方法来创建一个录音管理器实例,从而实现录音功能。 以下是一个示例,演示了如何在 UniApp 中使用 uni.getRecorderManager() 实现录音功能: // 在需要录音的页面或组…...

服务器数据恢复-LINUX操作系统下各文件系统误删除/格式化数据的恢复方案
服务器数据恢复环境: 基于EXT2/EXT3/EXT4/Reiserfs/Xfs文件系统的Linux操作系统。 服务器故障: LINUX操作系统下误删除/格式化数据。 服务器数据恢复过程: 1、首先会检测服务器是否存在硬件故障,如果检测出硬件故障,交…...
 、upper_bound,bisect_left,bisect_right))
python/C++二分查找库函数(lower_bound() 、upper_bound,bisect_left,bisect_right)
二分查找是一种经典的搜索算法,广泛应用于有序数据集中。它允许在大型数据集中高效地查找目标元素,减少了搜索的时间复杂度。本文将介绍在 C 和 Python 中内置的二分查找函数,让二分查找变得更加容易。 c lower_bound() 、upper_bound 定义…...

爬虫 — App 爬虫(二)
目录 一、Appium介绍二、node.js 安装三、Java 的 SDK 安装以及配置1、安装步骤2、配置环境变量 四、安卓环境的配置1、配置环境变量 五、Appium 安装1、安装2、打开 APP3、使用 六、Appium 使用1、定位数据(方法一,不常用)2、定位数据&#…...
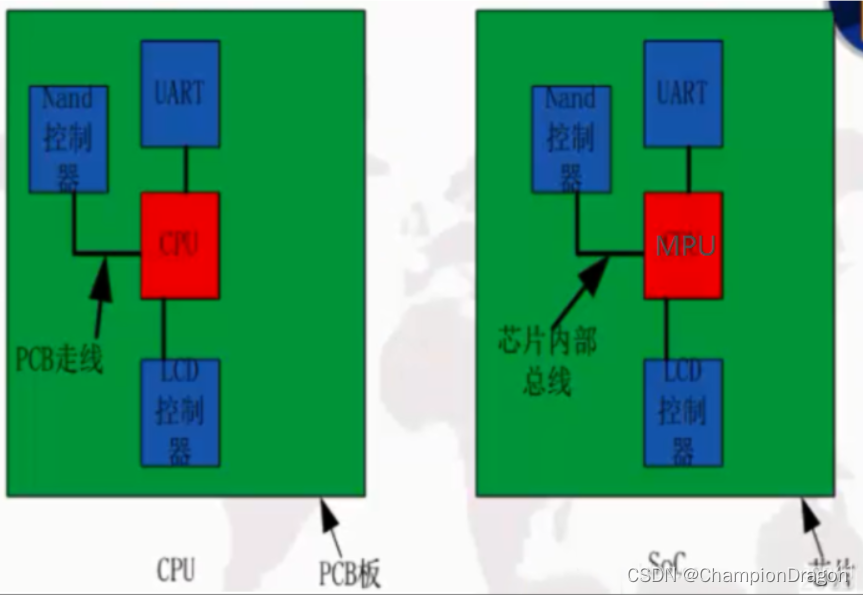
汽车电子相关术语
SOA SOA(Service-Oriented Architecture,面向服务的架构)是一种在计算机环境中设计、开发、部署和管理离散模型的方法。是由Garnter1996年提出的概念,将应用程序的不同功能单元(称为服务)进行拆分…...
Python 找出最大数
"""在输入的三个数中找出最大知识点:1、条件嵌套语句if/else2.字符串分割函数split()3、列表元素索引4、数据类型转换举一反三:1、如何控制只能输入三个数,否则重新输入2、如何避免输入无效字母"""# 定义一个变…...

Spring Security 用了那么久,你对它有整体把控吗?
文章目录 1.Servlet Filter:守门人的角色2.DelegatingFilterProxy:桥接 Servlet 和 Spring 的神器3.FilterChainProxy:Spring Security 过滤器链的管家3.SecurityFilterChain:Security 过滤器的串绳4.Spring Security 中的过滤器机…...

vue+minio实现文件上传操作
vueminio实现文件上传操作 minio文件上传vueminio实现文件上传操作 minio文件上传 minio文件上传有两种方法: 第一种是通过ak,sk,调用minio的sdk putObject进行文件上传;该方法支持go,java,js等各种语言&…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
