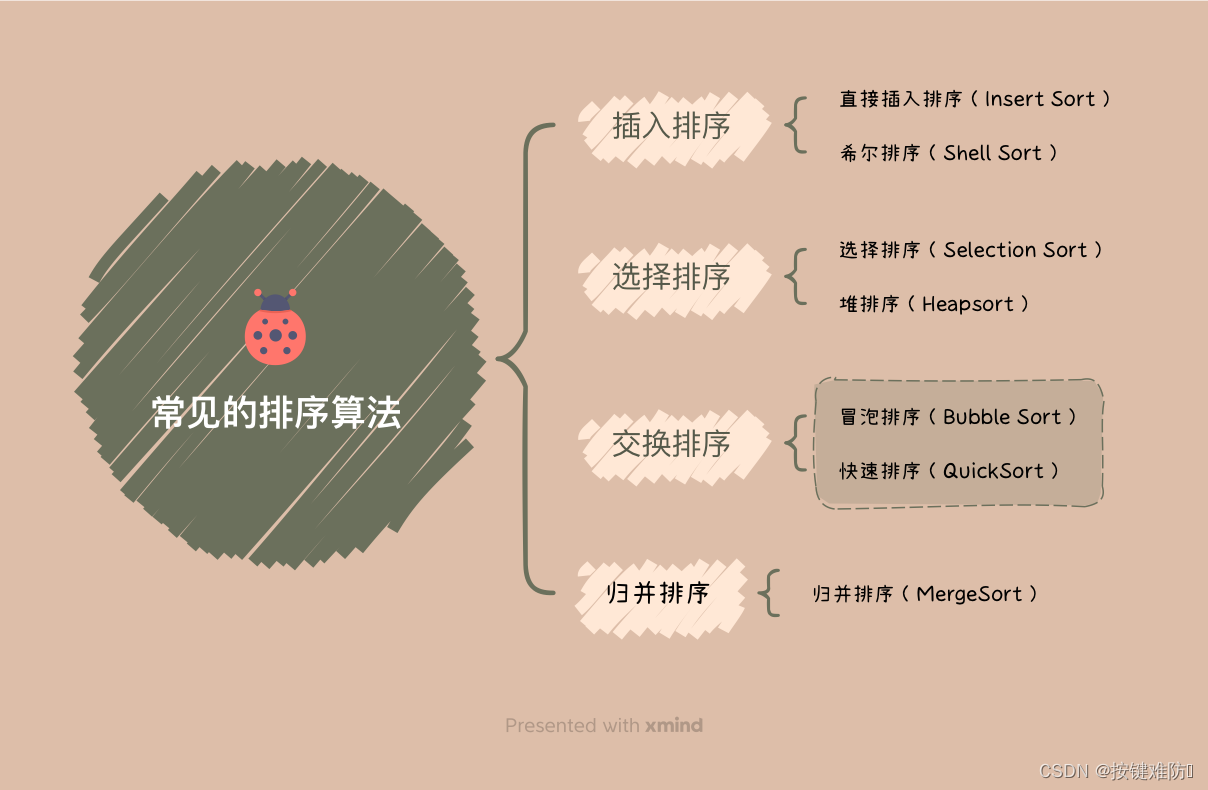
常见的排序算法 | 直接插入排序 | 希尔排序 | 选择排序 | 堆排序 | 冒泡排序 | 快速排序 | 归并排序 |(详解,附动图,代码)


思维导图:
一.插入排序
1.直接插入排序(InsertSort)
①手机通讯录时时刻刻都是有序的,新增一个电话号码时,就是使用插入排序的方法将其插入原有的有序序列。
②打扑克

步骤:
- ①如果一个序列只有一个数,那么该序列自然是有序的。插入排序首先将第一个数视为有序序列,然后把后面的元素视为要依次插入的序列。
- ②我们通过外层循环控制要插入的数(下标表示),从下标为1处的元素开始插入,直到最后一个元素,然后用insertVal保存要插入的值。
- ③内层循环负责交换,升序降序根据需求设计。
- ④内层循环结束,继续进行外层循环,插入下一个元素,进行排序,直到整个序列有序。
动图演示:
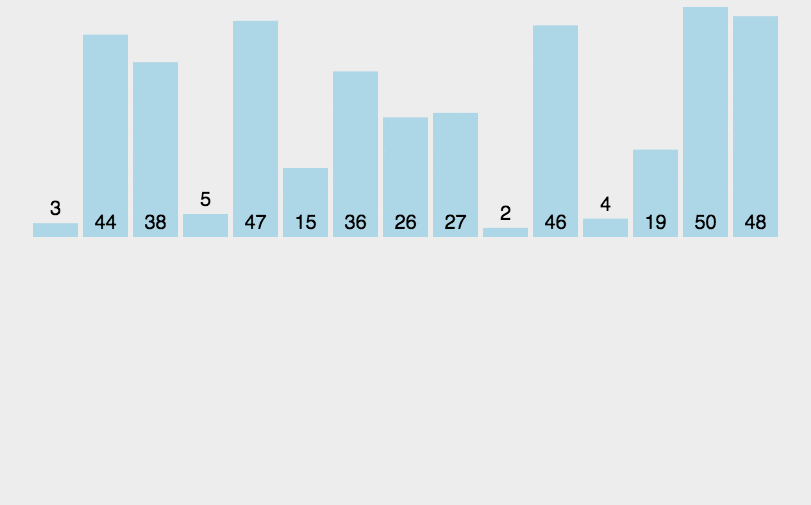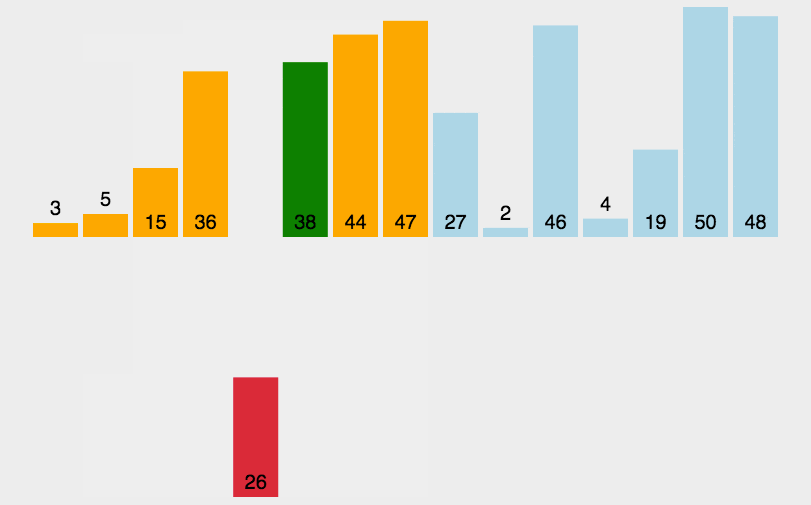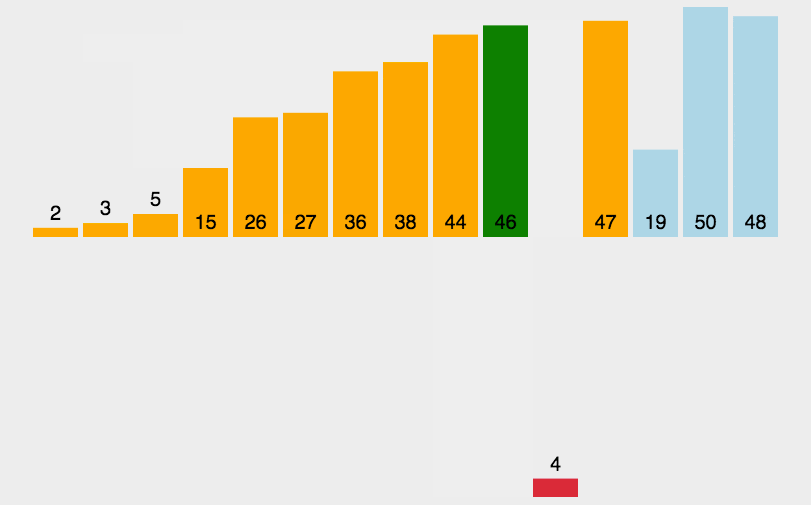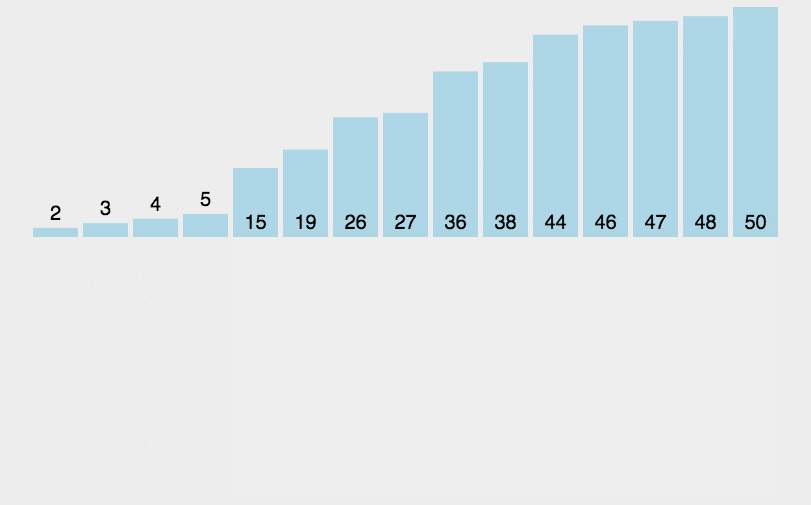

//插入排序
void InsertSort(int* arr, int n)
{int i, j, insertVal;for (i = 1; i < n; i++) //控制要插入的数{insertVal = arr[i];//先保存要插入的值//内层控制比较,j 要大于等于 0,同时 arr[j]大于 insertval 时,arr[j]位置元素往后覆盖for (j=i-1; j >= 0 && arr[j] > insertVal; j--){arr[j + 1] = arr[j];}arr[j + 1] = insertVal;//将insertVal插入两个极端情况//1.前面的数字小于insertVal,不进入内层循环,直接原地不动//2.前面的数字都大于insertVal,x放在下标为0处}
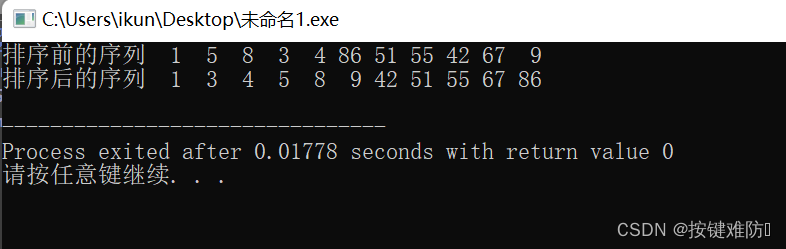
}效果:
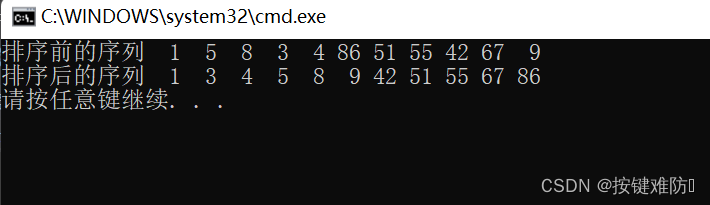
结论:
- 1. 元素集合越接近有序,直接插入排序算法的时间效率越高
- 2. 时间复杂度:O(N^2)
- 3. 空间复杂度:O(1),它是一种稳定的排序算法
- 4. 稳定性:稳定
2.希尔排序(Shellsort)
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。
步骤:
- 1.对待排序的序列进行预排,让序列接近有序。
- 预排也是借助直接插入排序实现,具体实现方法,规定一个增量(gap),间隔为gap的元素为一组,然后分组排序,直到间隔gap的所有分组排序完成,增量(gap)减少,继续间隔为gap的元素进行分组排序 ,当增量减至1时,预排完成。
- gap越大,大的数可以越快的到后面,小的数可以越快的到前面。
gap越大,预排完越不接近有序。
gap越小,越接近有序。- 2.gap=1,直接进行直接插入排序。
动图: 

//希尔排序
void ShellSort(int* arr, int n)
{int gap=n;int i ,insertVal;while (gap> 1){//每次对gap折半操作gap = gap / 2;//间隔为gap的所有组进行插入排序for (i = 0; i < n-gap; i++){//组员i+gap(下标)最大到n-1,再多就越界访问了,所以i<=n-1-gap,上面是开区间表示insertVal = arr[i+gap];for (i; i >= 0 && arr[i] > insertVal; i-=gap){arr[i+gap] = arr[i];}arr[i+gap] = insertVal;}
}
}
希尔排序的特性总结:
- 1. 希尔排序是对直接插入排序的优化。
- 2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的 了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的 对比。
- 3. 希尔排序的时间复杂度不好计算,需要进行推导,推导出来平均时间复杂度: O(N^1.3— N^2)
- 4. 稳定性:不稳定
二.选择排序
3.选择排序(SelectSort)
步骤:
遍历一遍,从待排序列中选出一个最小值,然后放在序列的起始位置,再找次小的,直到整个序列排完。
动图演示:
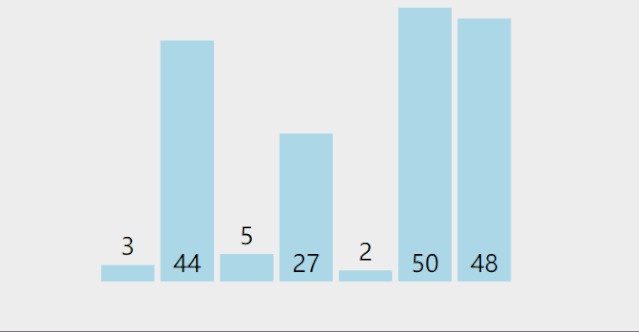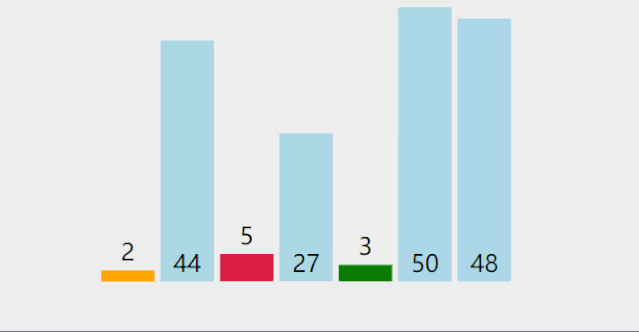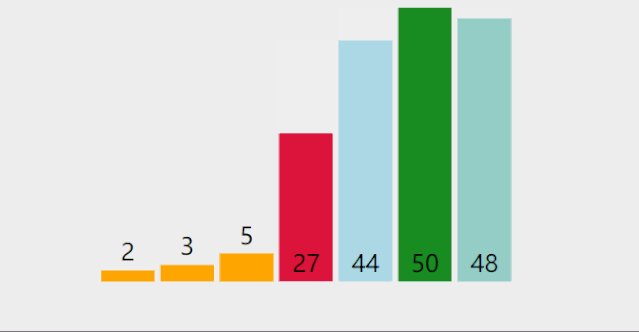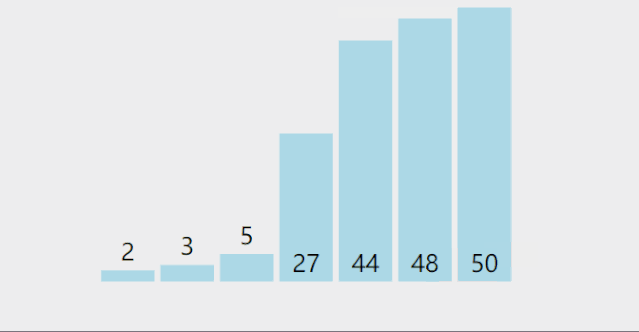
但这种太慢了,实际上,我们可以一趟选出两个值,一个最大值一个最小值,然后将其放在序列开头和末尾,这样可以使选择排序的效率快一倍。

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//选择排序
void SelectSort(int* arr, int n)
{int begin = 0, end = n - 1;while (begin < end){int mini = begin, maxi = begin;//初始化,让最大值和最小值起初都是自己,作为一个基准for (int i = begin; i <= end; i++){if (arr[i] < arr[mini]){mini = i;//不断更新在此次遍历过程中遇到的最小值}if (arr[i] > arr[maxi]){maxi = i;//不断更新在此次遍历过程中遇到的最大值}}Swap(&arr[begin], &arr[mini]);//此次遍历最小的放到begin处//注意:最小值已经放到了begin处,但如果begin原先存的是此次遍历最大的数//那么你一交换,把最大的数给交换到了,mini处,所以我们要修正if (begin == maxi){// 如果begin跟maxi重叠,需要修正一下maxi的位置maxi = mini;}Swap(&arr[maxi], &arr[end]);//此次遍历最大的放到end处begin++;end--;}
}效果:
直接选择排序的特性总结:
- 1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 2. 时间复杂度:O(N^2)
- 3. 空间复杂度:O(1)
- 4. 稳定性:不稳定
4.堆排序(HeapSort)
堆排序即利用堆的思想来进行排序
堆的性质:
• 堆中某个节点的值总是不大于或不小于其父节点的值
• 堆总是一棵完全二叉树
步骤:
- 升序:建大堆,若父结点的值恒大于等于子结点的值,则该堆称为最大堆(max heap)
- 降序:建小堆,若父结点的值恒小于等于子结点的值,则该堆称为最小堆(min heap);
①建堆:
堆的逻辑结构是一个完全二叉树,存储结构是数组,所以数组也可以看成一个堆,但还不满足堆的性质,而我们要做的就是调整数组,使之建堆成最大堆或最小堆
调整方法使用向下排序算法。
向下调整算法的核心思想:选出左右孩子中小的哪一个,跟父亲交换,如果要建大堆则相反
向下调整算法的前提:建小堆,左右子树都必须是小堆,才能够进行调整,大堆相反。
但数组满足不了这个前提,我们就换一种思想,从倒数第一个非叶子结点(最后一个结点的父亲)开始调整。
②排序
假设我们建的是大堆,父结点的值恒大于等于子结点的值,然后按照堆删的思想将堆顶和堆底的数据交换,但不同的是这里不删除最后一个元素。这样最大元素就在最后一个位置,然后从堆顶向下调整到倒数第二个元素,这样次大的元素就在堆顶,重复上述步骤直到只剩堆顶时停止。
数组确定父子关系:
lchild(左孩子)=parent(父亲)*2+1
rchild(右孩子)=parent(父亲)*2+2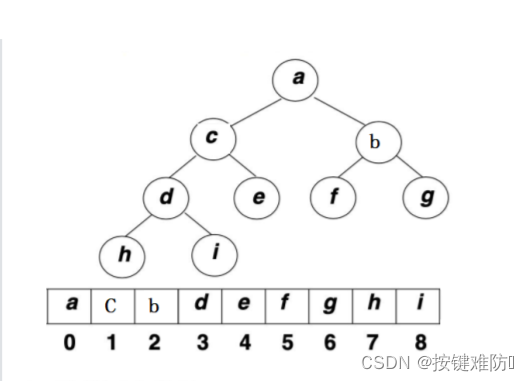
动图演示:


//建堆
void AdjustDown(int* arr, int n, int root)//向下调整
{int parent = root;int child = parent * 2 + 1;while (child < n){if (child + 1 < n && arr[child + 1] > arr[child]){child++;}if (arr[child] > arr[parent]){Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
//堆排序
void HeapSort(int* arr, int n)
{//建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, n, i);}//交换for (int i = n - 1; i > 0; i--){Swap(&arr[i], &arr[0]);AdjustDown(arr, i, 0);}
}堆排序的特性总结:
- 1. 堆排序使用堆来选数,效率就高了很多。
- 2. 时间复杂度:
- 3. 空间复杂度:O(1)
- 4. 稳定性:不稳定
三.交换排序
5.冒泡排序(BubbleSort)
两两相邻元素进行比较,并且可能需要交换,一趟下来该趟的最大(小)值在最右边。
动图演示:
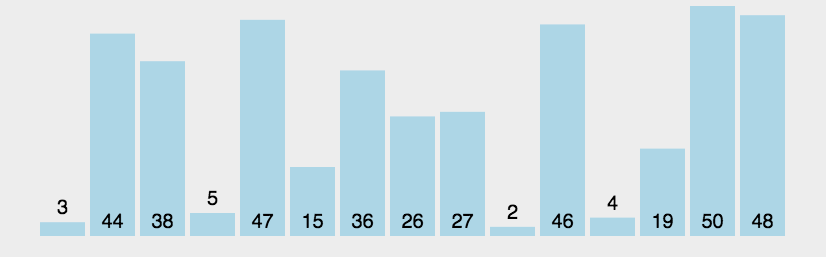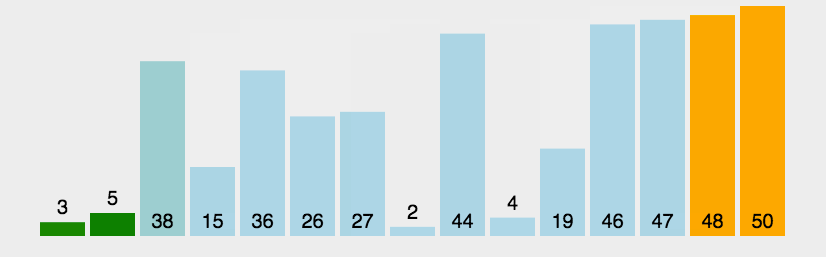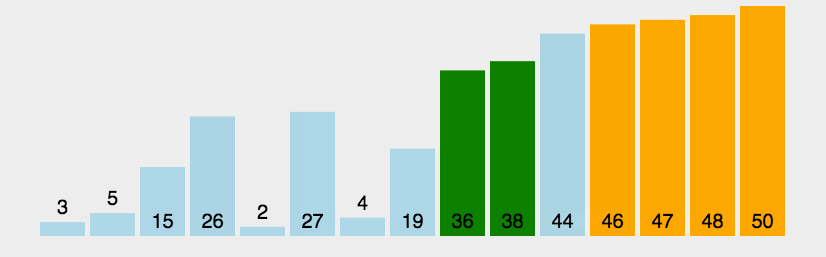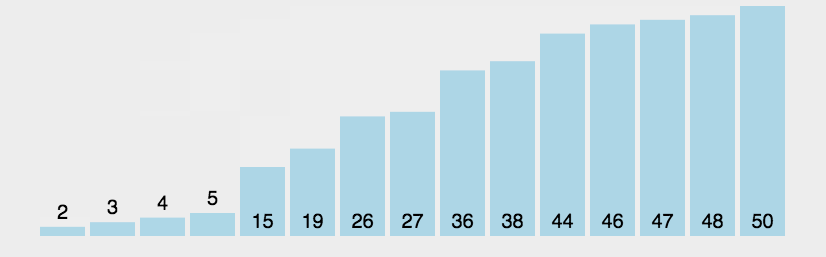

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//冒泡排序
void BubbleSort(int* arr, int n)
{for (int i = 0; i < n; i++)//控制趟数{int exchange = 0;//记录交换次数for (int j = 0; j < n - 1 - i; j++){//第一趟比较n-1次,然后每走完i趟,就有i个右边的位被占,所以比较次数减iif (arr[j] > arr[j + 1]){Swap(&arr[j], &arr[j + 1]);exchange = 1;}}if (exchange == 0){//交换次数为0,排序直接结束break;}}
}
冒泡排序的特性总结:
- 1. 冒泡排序是一种非常容易理解的排序
- 2. 时间复杂度:O(N^2)
- 3. 空间复杂度:O(1)
- 4. 稳定性:稳定
6.快速排序(QuickSort)
【递归实现】:
快速排序的核心是分治思想:
假设我们的目标依然是按从小到大的顺序排列,我们找到数组中的一个分割值,把比分割值小的数都放在数组的左边,把比分割值大的数都放在数组的右边,这样分割值的位置就被确定。借助分割值的位置把数组一分为二,前一半数组和后一半数组继续找分割值的位置, 不断地进行递归,最终分割得只剩一个时,整个序列自然就是有序的。
重点在于怎么确定分割值的位置,下面有挖坑法,左右指针法,和前后指针法三种方法。
6.1挖坑法
挖坑法确定分割值的位置
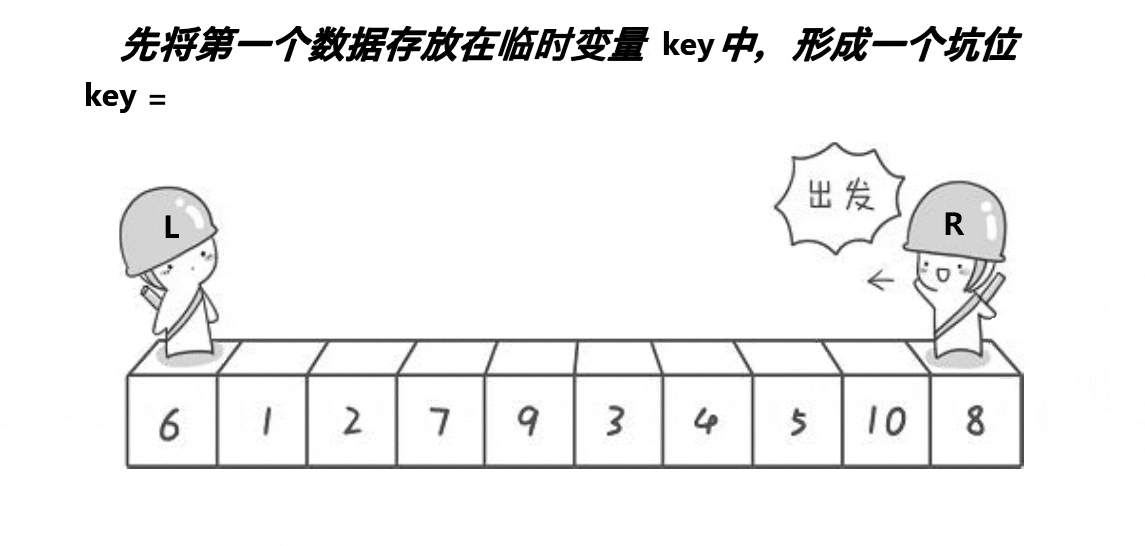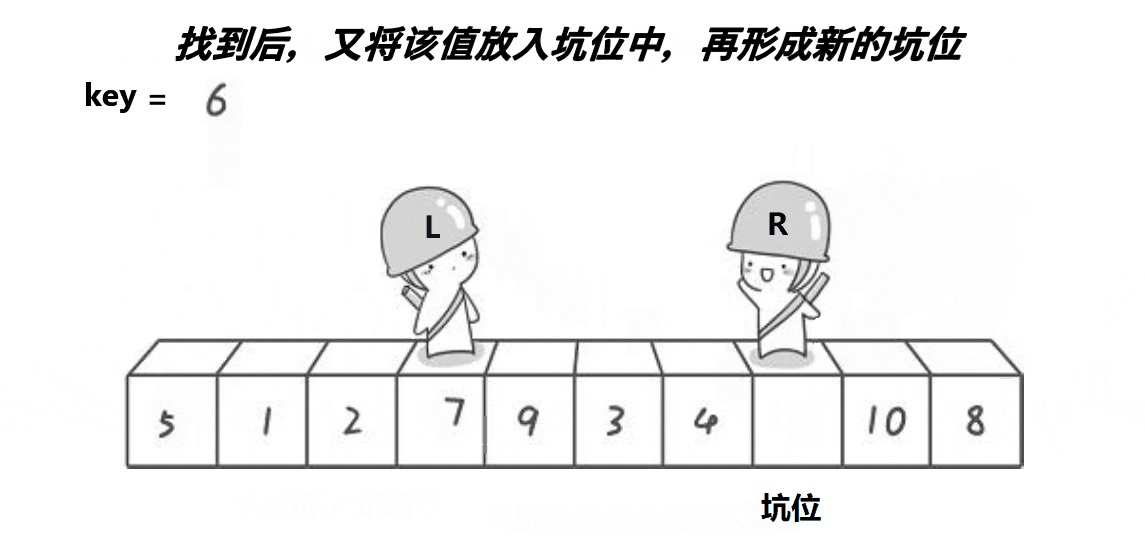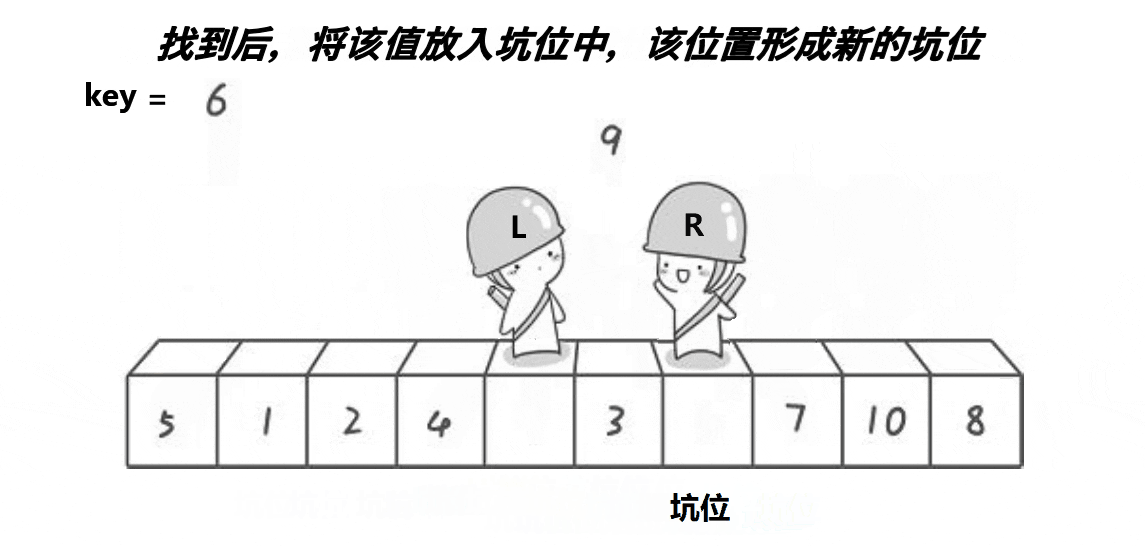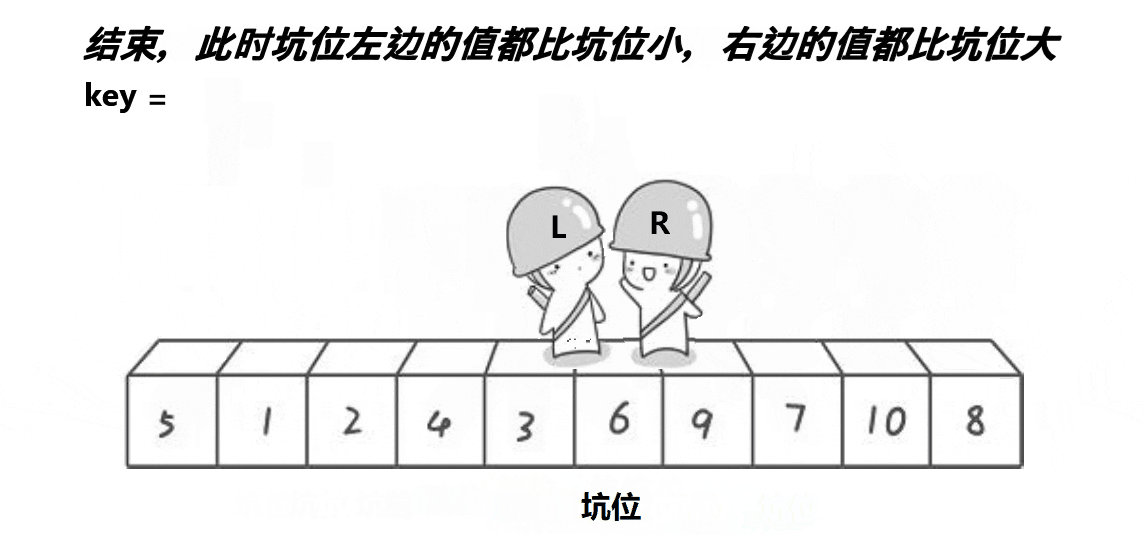
步骤:
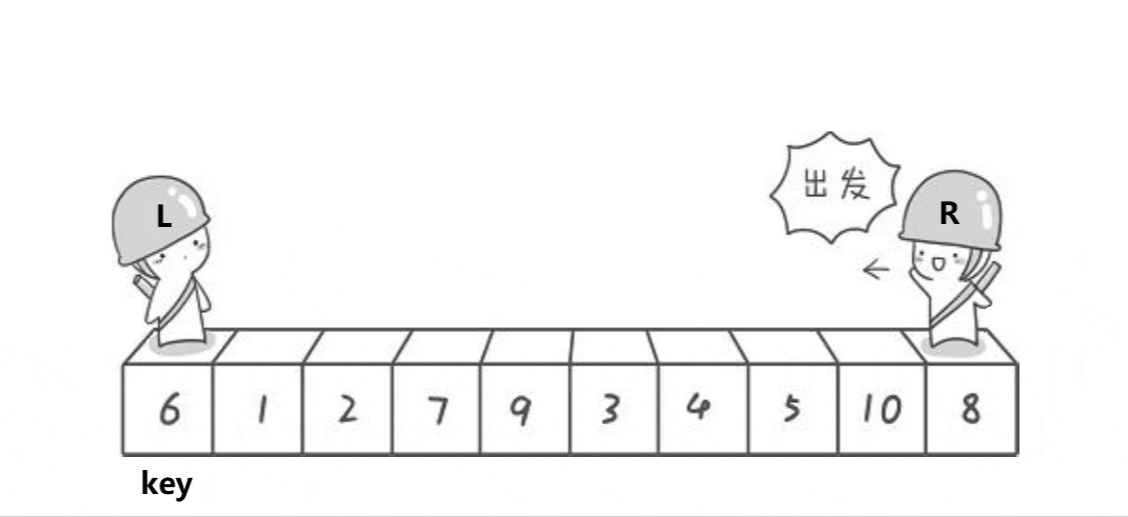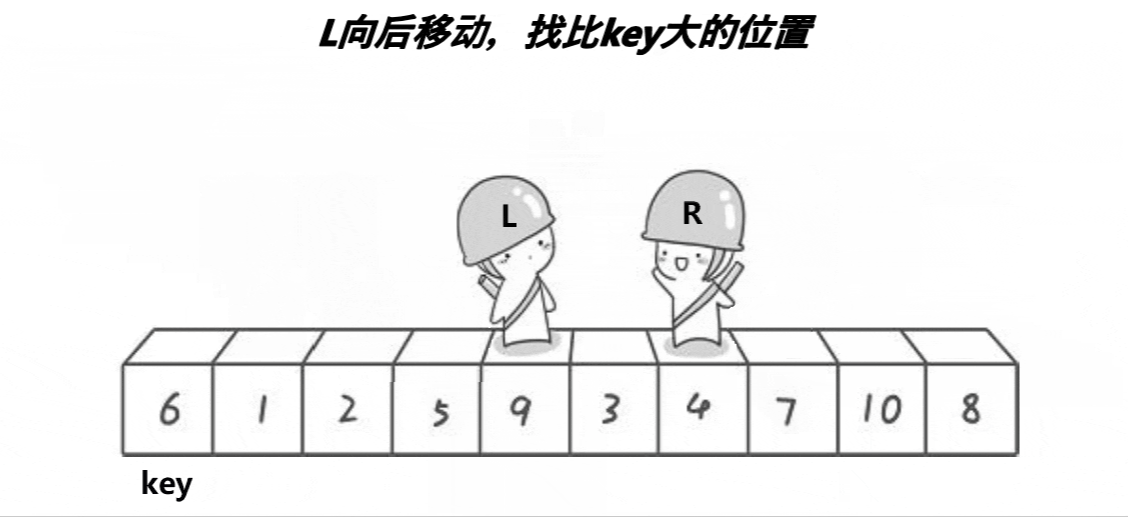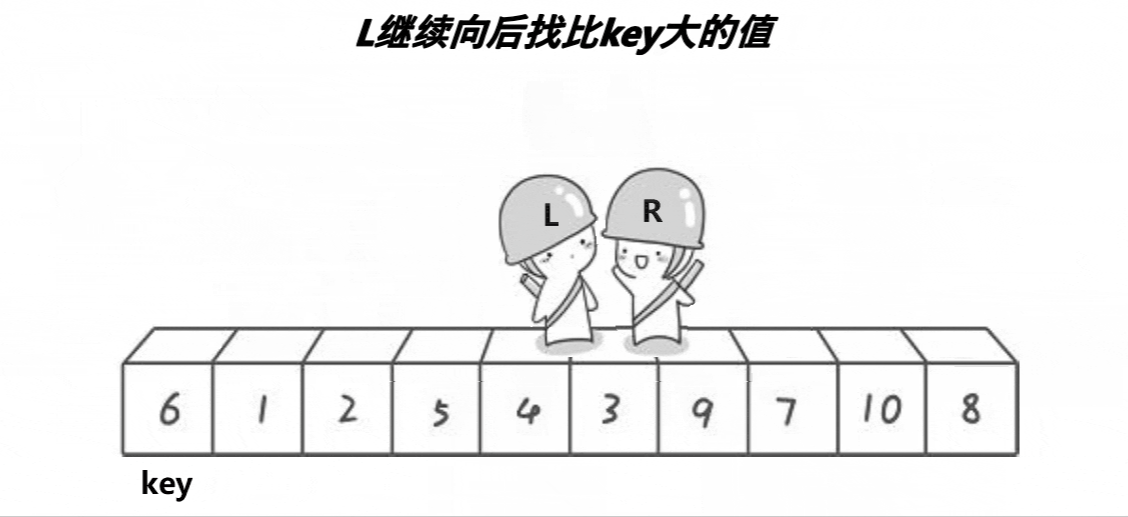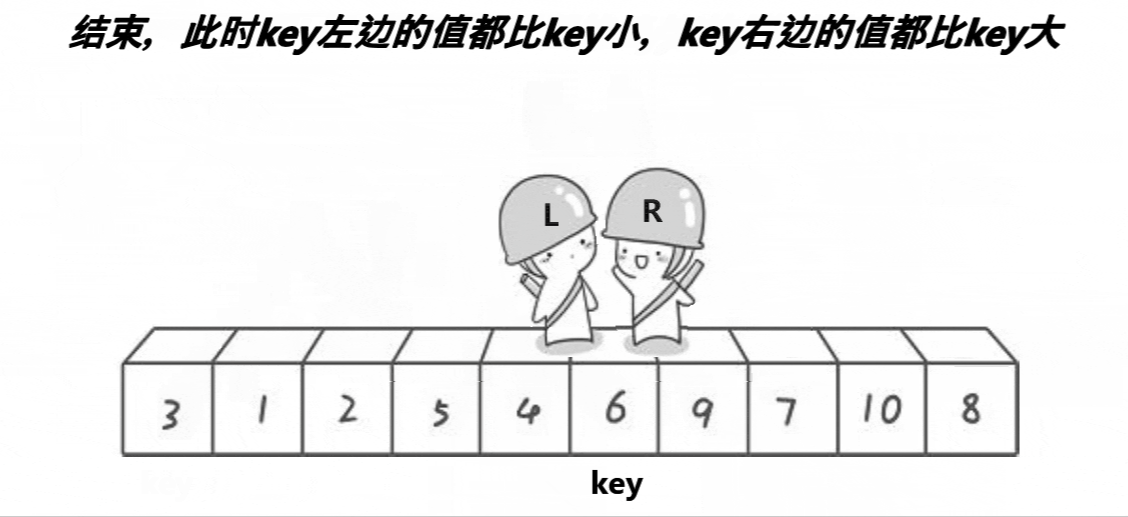
- ①定义一个分割值key,一般是将待排序序列的最左边或最右边的数据取出赋给key,(下面以最左面为例)那么最最左边数据就可以被覆盖,就是所谓的坑。
- ②left代表待排序序列最左端,right代表待排序序列最右端
- ③首先坑在最左边,所以我们让right先走,去找比key小的值,放到最左边的坑,然后此时的right变成了坑,所以left在走,找比key大的值,放到此时的right,然后right再走,找比key小的值,放到此时的left,如此进行下去,直到left和right最终相遇,将key放到相遇点这个坑,这时相遇点就是分割值的位置。
- ④借助分割值的位置把数组一分为二,前一半数组和后一半数组继续采用这种思想, 不断地进行递归,最终分割得只剩一个时,整个序列自然就是有序的。
动图演示:

//挖坑法确定分割值的位置
int PartSort1(int* arr, int left, int right)
{int key = arr[left];//取出分割值int hole = left;//保存坑的位置while (left < right){// 右边找小,放到左边while (left < right && arr[right] >= key){right--;}// 不满足上边的循环,就说明右边的right有小的要放到左边的left坑里 arr[hole] = arr[right];hole = right;//更新坑的位置// 左边找大while (left < right && arr[left] <= key){left++;}// 不满足上边的循环,就说明左边begin有大的放到右边end的坑里arr[hole] = arr[left];hole = left;}arr[hole] = key;return hole;//本次排序完成,返回分割值key的下标
}
//快速排序
void QuickSort(int* arr, int left, int right)
{if (left >= right){//递归停止的条件return;}int keyi = PartSort1(arr, left, right);//每一趟排序完成都会返回一个分割值key的下标//借助分割值的位置将序列分为左子区间[left,keyi-1]和右子区间[keyi+1,right]//再用分治递归使左子区间和右子区间有序QuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);
}效果:

6.2左右指针法
左右指针法确定分割值的位置
步骤:
- ①选定一个分割值key,一般是待排序序列的最左边或最右边。
- ②left代表待排序序列最左端,right代表待排序序列最右端
- ③假设key在最左边,那么right先走遇到比key小的值就停下,不发生交换,然后left开始走,直到left遇到一个大于key的数时,将left和right的内容交换,right再次开始走,如此进行下去,直到left和right最终相遇,此时将相遇点的内容与key的内容交换即可,这时相遇点就是分割值的位置。
- ④借助分割值的位置把数组一分为二,前一半数组和后一半数组继续采用这种思想, 不断地进行递归,最终分割得只剩一个时,整个序列自然就是有序的。
动图演示:

//左右指针法确定key的位置
int PartSort2(int* arr, int left, int right)
{int key =left;//选定分割值while (left < right){// 找小while (left < right && arr[right] >=arr[key]){right--;}// 找大while (left < right && arr[left] <=arr[key]){left++;}Swap(&arr[left], &arr[right]);} Swap(&arr[left], &arr[key]);return left;//本次排序完成,返回分割值key的下标
}
//快速排序
void QuickSort(int* arr, int left, int right)
{if (left >= right){//递归停止的条件return;}int keyi = PartSort2(arr, left, right);//每一趟排序完成都会返回一个分割值key的下标//借助分割值的位置将序列分为左子区间[left,keyi-1]和右子区间[keyi+1,right]//再用分治递归使左子区间和右子区间有序QuickSort(arr, left, keyi- 1);QuickSort(arr, keyi+ 1, right);
}6.3前后指针法
前后指针版本确定分割值的位置
步骤:
- ①规定一个分割值key,一般是最左边或是最右边的。
- ②起始时,prev指针指向序列开头,cur指针指向prev+1。
- ③cur从左至右遍历,若cur指向的内容小于key,则prev先向后移动一位,然后交换prev和cur指针指向的内容,然后cur指针++;若cur指向的内容大于key,则cur指针直接++。如此进行下去,直到cur到达end位置,此时将key和prev++指针指向的内容交换即可。
- 4.这样做本质上就是cur指针遍历一遍待排序序列,把所有小于key的数据都放到下标[1,prev]这个区间,然后把key和prev的内容交换。
- 5.key将待排序序列该分成了两半,左边比他小,右边比他大,然后再让左右序列进行上述操作,直至左右序列分割得只剩一个元素时,整个序列自然就是有序的。

//前后指针版本确定分割值的位置
int PartSort3(int* arr, int left, int right)
{int key =left;//选定分割值int cur=left+1;int prev=left;while(cur<=right){while(arr[cur]<arr[key]&&++prev!=cur){//只要a[cur]<a[key]语句为真,prev必须要进行++,但不一定要发生交换,因为prev++=cur,自己和自己交换没意义。Swap(&arr[cur],&arr[prev]);} cur++; } Swap(&arr[key], &arr[prev]);return prev;//本次排序完成,返回分割值key的下标
}
//快速排序
void QuickSort(int* arr, int left, int right)
{if (left >= right){//递归停止的条件return;}int keyi = PartSort3(arr, left, right);//每一趟排序完成都会返回一个分割值key的下标//借助分割值的位置将序列分为左子区间[left,keyi-1]和右子区间[keyi+1,right]//再用分治递归使左子区间和右子区间有序QuickSort(arr, left, keyi- 1);QuickSort(arr, keyi+ 1, right);
}
6.4快速排序的优化
1.我们在分割值的选择上可以进行优化,假如我要实现升序,原待排序序列接近降序,这就会造成效率太低,递归次数过多,导致栈溢出。所以我们可以选出一个中间值和最左(右)边交换。
方法:三数取中
//三数取中
int MidIndex(int* a, int left, int right)
{int mid = (left + right) / 2;//防止mid越界//int mid = left+(right - left) / 2;if (a[left] < a[right]){if (a[mid] < a[left]){return left;}else if (a[mid] > a[right]){return right;}else{return mid;}}else{if (a[mid] > a[left]){return left;}else if (a[mid] < a[right]){return right;}else{return mid;}}
}2.减少递归次数,方法:小区间优化
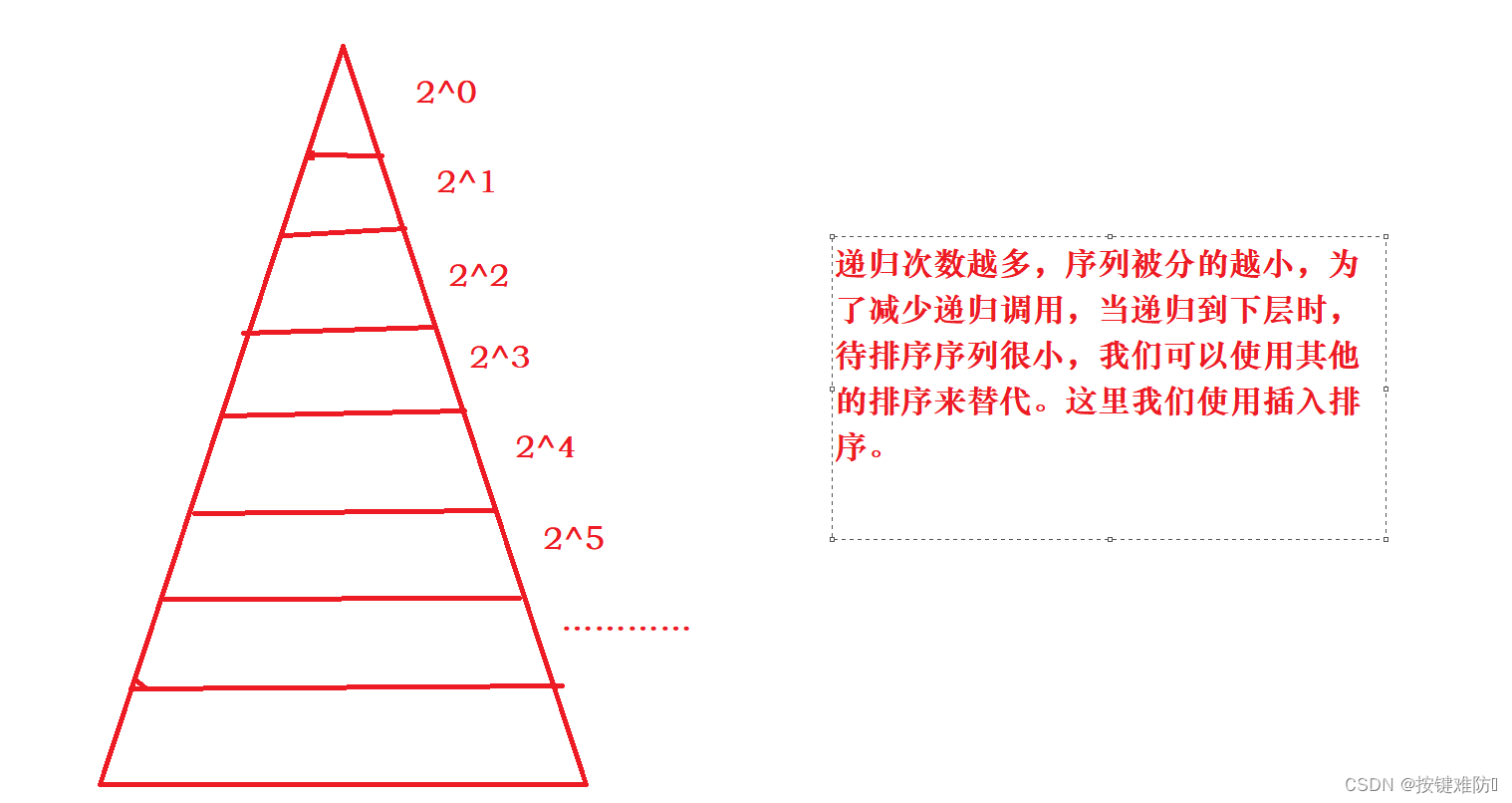
以左右指针法举例
// 三数取中
int GetMidIndex(int* a, int left, int right)
{int mid = (left + right)/2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}else // a[left] > a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]){return left;}else{return right;}}
}
//左右指针法确定key的位置
int PartSort2(int* arr, int left, int right)
{int mid = GetMidIndex(arr, left, right);//将分割值调整至最左边Swap(&arr[mid], &arr[left]);int key =left;//选定分割值while (left < right){// 找小while (left < right && arr[right] >=arr[key]){right--;}// 找大while (left < right && arr[left] <=arr[key]){left++;}Swap(&arr[left], &arr[right]);} Swap(&arr[left], &arr[key]);return left;//本次排序完成,返回分割值key的下标
}
//快速排序
void QuickSort(int* arr, int left, int right)
{if (left >= right){return;}//小区间优化,,减少递归次数if (right - left + 1 < 10){InsertSort(arr + left, right -left + 1);}else{int keyi = PartSort2(arr, left, right);//每一趟排序完成都会返回一个分割值key的下标//借助分割值的位置将序列分为左子区间[left,keyi-1]和右子区间[keyi+1,right]//再用分治递归使左子区间和右子区间有序QuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);}
}【非递归版本】
我们可以借助栈的思想,递归是一直递到限制条件,然后开始回归,最后一次调用先完,然后倒数第二次……,和栈的先进后出思想很像所以我们可以借助栈来实现。
6.5栈实现
typedef int STDataType;
typedef struct Stack
{STDataType* a;int top;int capacity;
}ST;
void StackInit(ST* ps)
{assert(ps);ps->a = (STDataType*)malloc(sizeof(STDataType)* 4);if (ps->a == NULL){printf("malloc fail\n");exit(-1);}ps->capacity = 4;ps->top = 0;
}void StackDestory(ST* ps)
{assert(ps);free(ps->a);ps->a = NULL;ps->top = ps->capacity = 0;
}
// 入栈
void StackPush(ST* ps, STDataType x)
{assert(ps);// 满了-》增容if (ps->top == ps->capacity){STDataType* tmp = (STDataType*)realloc(ps->a, ps->capacity * 2 * sizeof(STDataType));if (tmp == NULL){printf("realloc fail\n");exit(-1);}else{ps->a = tmp;ps->capacity *= 2;}}ps->a[ps->top] = x;ps->top++;
}// 出栈
void StackPop(ST* ps)
{assert(ps);// 栈空了,调用Pop,直接中止程序报错assert(ps->top > 0);//ps->a[ps->top - 1] = 0;ps->top--;
}STDataType StackTop(ST* ps)
{assert(ps);// 栈空了,调用Top,直接中止程序报错assert(ps->top > 0);return ps->a[ps->top - 1];
}int StackSize(ST* ps)
{assert(ps);return ps->top;
}bool StackEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}
//前后指针版本确定分割值的位置
int PartSort1(int* arr, int left, int right)
{int key = arr[left];//取出分割值int hole = left;//保存坑的位置while (left < right){// 右边找小,放到左边while (left < right && arr[right] >= key){right--;}// 不满足上边的循环,就说明右边的right有小的要放到左边的left坑里 arr[hole] = arr[right];hole = right;//更新坑的位置// 左边找大while (left < right && arr[left] <= key){left++;}// 不满足上边的循环,就说明左边begin有大的放到右边end的坑里arr[hole] = arr[left];hole = left;}arr[hole] = key;return hole;//本次排序完成,返回分割值key的下标
}
// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)
{//创建栈Stack st;StackInit(&st);//原始数组区间入栈StackPush(&st, right);StackPush(&st, left);//将栈中区间排序while (!StackEmpty(&st)){//注意:如果right先入栈,栈顶为leftleft = StackTop(&st);StackPop(&st);right = StackTop(&st);StackPop(&st);//得到分割值的下标int keyi = PartSort1(a, left, right);// 以分割值下标分割点,形成左右两部分//分别入栈if (right > keyi + 1){StackPush(&st, right);StackPush(&st, keyi + 1);}if (left < keyi - 1){StackPush(&st, keyi - 1);StackPush(&st, left);}}StackDestory(&st);
}快速排序的特性总结:
- 1. 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 2. 时间复杂度:
- 3. 空间复杂度:
- 4. 稳定性:不稳定
四.归并排序
7.归并排序(MergeSort)
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。 将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
步骤:
使用归并的前提是所有子序列都有序,所以我们对待排序序列进行分割,一分二,二分四…………直至子序列只有一个数字,一个数字总该认为他有序吧。 将已有序的子序列合并,得到完全有序的序列;注意:(两个子序列合并成一个子序列,序列要进行排序,确保该子序列有序,以便后续合并),若将两个有序表合并成一个有序表,称为二路归并。
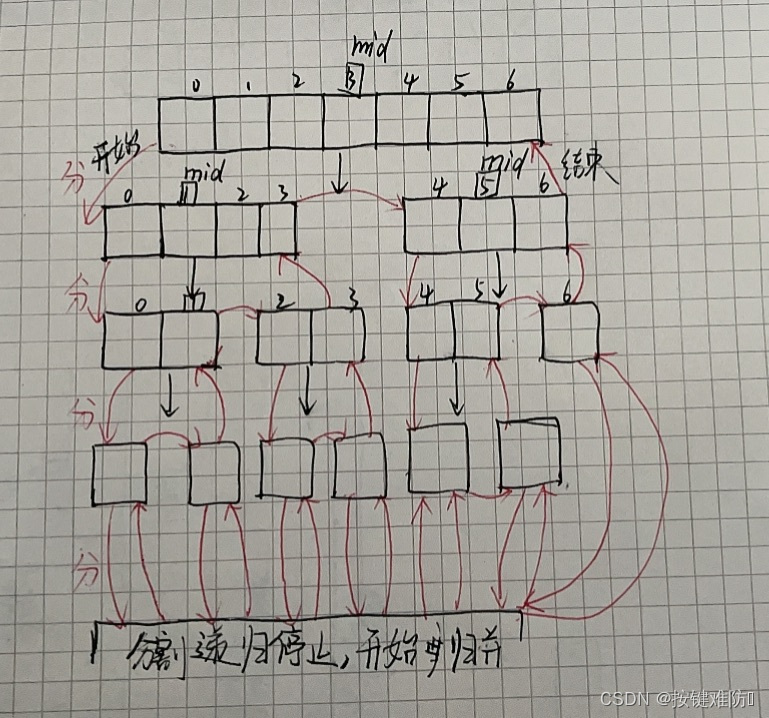
动图演示:
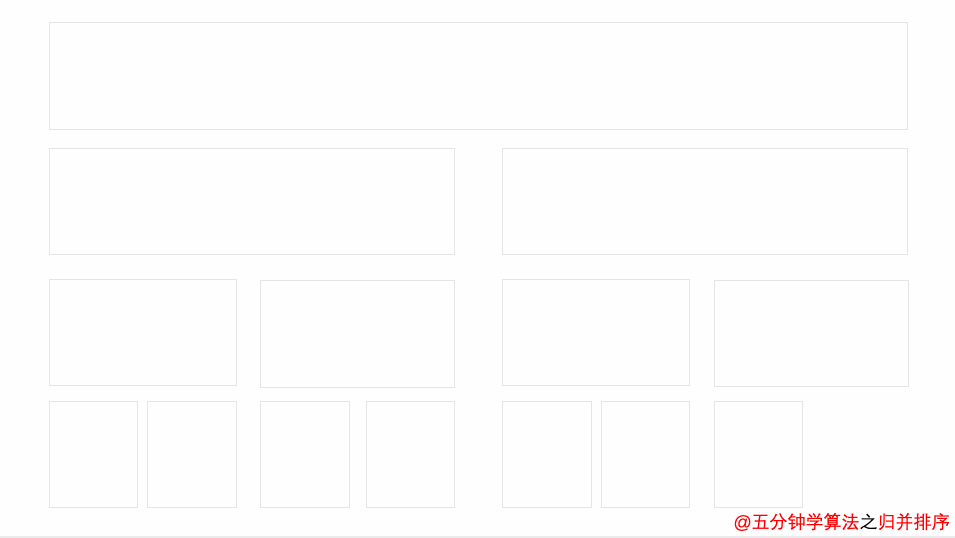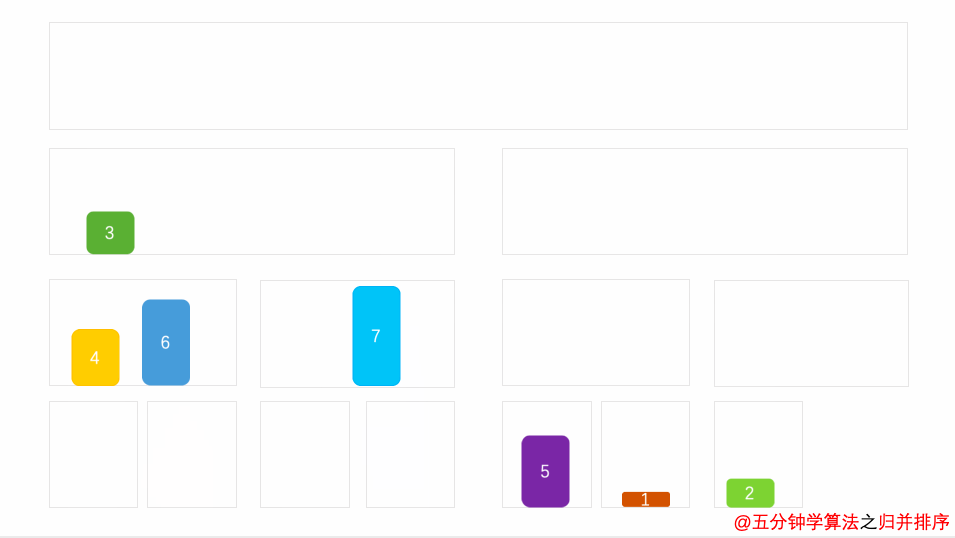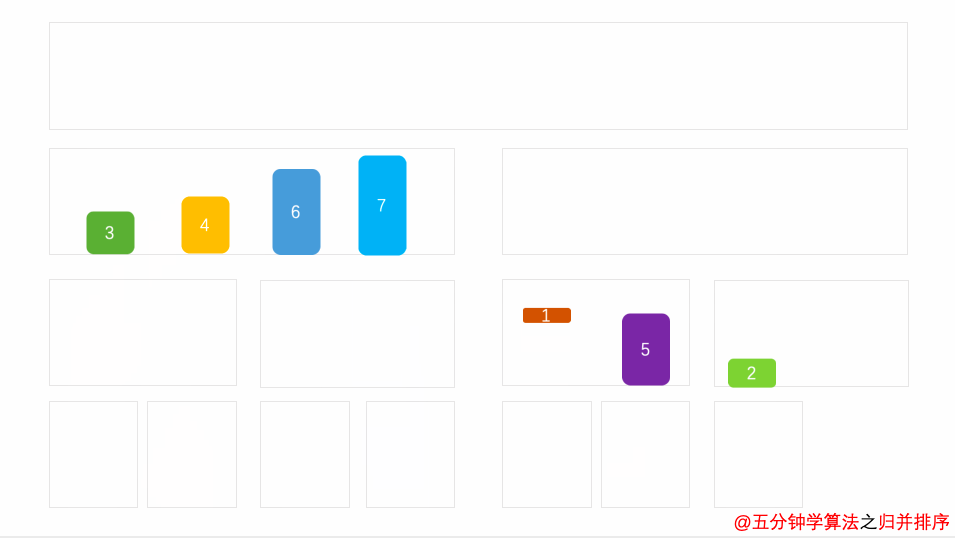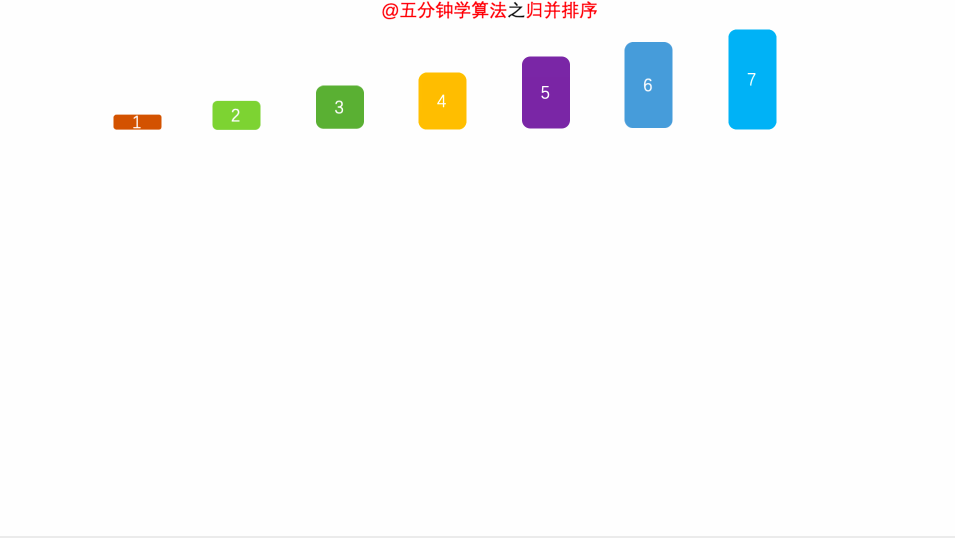

void _MergeSort(int* arr, int left, int right, int* tmp)
{if (left >= right){//子序列分割只剩一个元素,停止,跳到上一级归并return;}int mid = (left + right) >> 1;//分割,一分二……_MergeSort(arr, left, mid, tmp);//划分左区间[left, mid]_MergeSort(arr, mid+1, right, tmp);//划分右区间[mid+1, right]//分割完成开始归并int begin1 = left, end1 = mid;//左区间int begin2 = mid + 1, end2 = right;//右区间int index = left;while (begin1 <= end1 && begin2 <= end2){//注意结束条件为一个序列为空时就停止//合并的序列可能不一样长if (arr[begin1] < arr[begin2]){//为了实现合并后的子序列有序,我们要对要合并的两个序列的元素进行一一比较,比较结果放到 //临时数组,然后再把临时数组赋给原序列。tmp[index++] = arr[begin1++];//一定是后置++,复制完确保指向下一个元素}else{tmp[index++] = arr[begin2++];}}//两序列不可能同时为空,可能有瘸腿的情况,将剩余元素合并while (begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}//将合并后的序列拷贝到原数组中//在这里拷贝的原因是保证返回到上一层递归后两个子序列中的元素是有序的for (int i = left; i <= right; ++i){arr[i] = tmp[i];}
}
//归并排序
void MergeSort(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int)*n);//临时数组,左右区间归并时排序要借助临时数组//防止覆盖待排序序列,造成错误if (tmp == NULL){perror("malloc");exit(-1);} _MergeSort(arr, 0, n - 1, tmp);//分割归并free(tmp);tmp=NULL;
}归并排序的特性总结:
- 1. 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问 题。
- 2. 时间复杂度:
- 3. 空间复杂度:O(N)
- 4. 稳定性:稳定
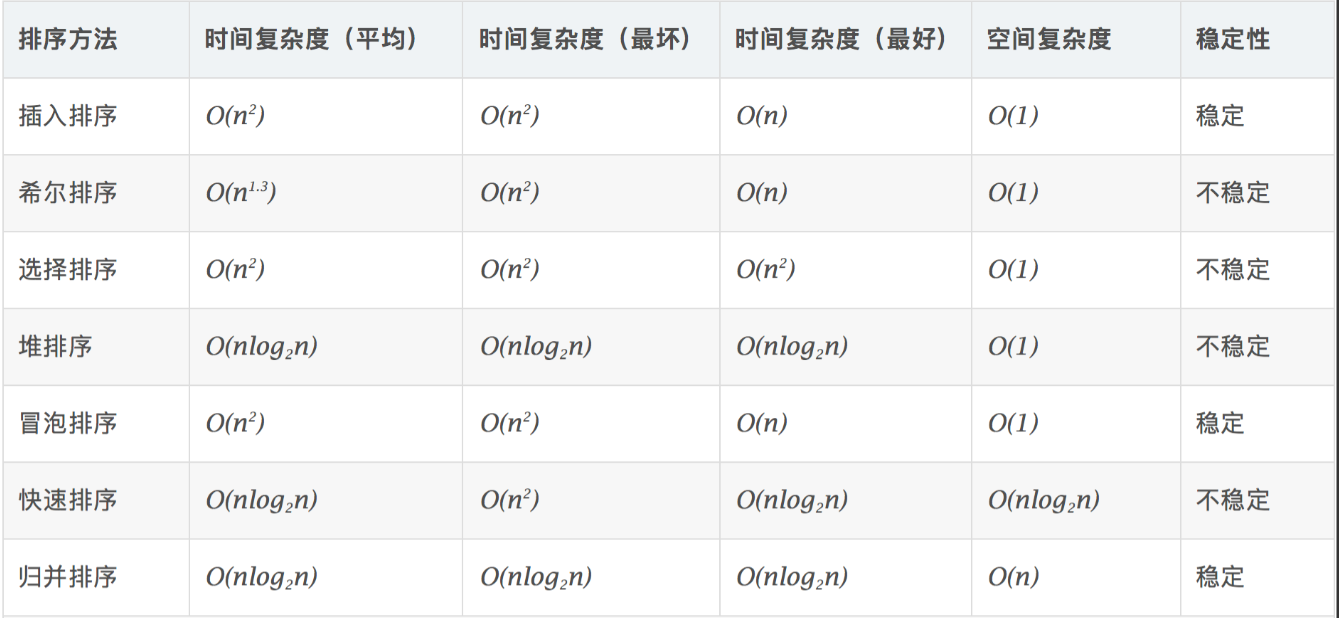
排序算法复杂度及稳定性分析:
博主水平有限,如有错误还请多多包涵。

相关文章:

常见的排序算法 | 直接插入排序 | 希尔排序 | 选择排序 | 堆排序 | 冒泡排序 | 快速排序 | 归并排序 |(详解,附动图,代码)
思维导图: 一.插入排序 1.直接插入排序(InsertSort) ①手机通讯录时时刻刻都是有序的,新增一个电话号码时,就是使用插入排序的方法将其插入原有的有序序列。 ②打扑克 步骤: ①如果一个序列只有一个数&am…...
深入浅出 MySQL 索引(一)
MySQL 索引(基础篇) 你好,我是悟空。 本文目录如下: 一、前言 最近在梳理 MySQL 核心知识,刚好梳理到了 MySQL 索引相关的知识,我的文章风格很多都是原理 实战的方式带你去了解知识点,所以…...

FinClip 的 2022 与 2023
相比往年,今年复盘去年与展望新年的文章来的稍慢一点。不过也希望能够借这篇文章,和关注 FinClip 的用户朋友们一起聊聊,我们在去年和今年的想法与计划。 2022 在过去的一年中,我们的身边发生了很多事情,这些事情在不…...
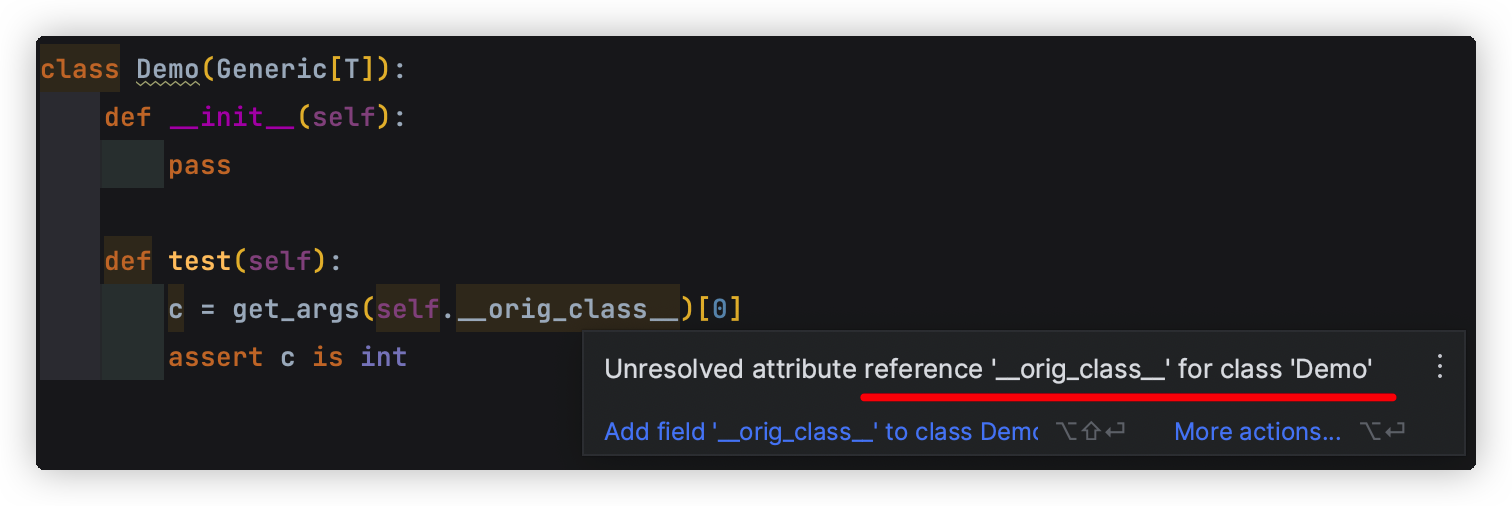
Python 泛型 - 如何在实例方法中获取泛型参数T的类型?
先上解决方法:https://stackoverflow.com/questions/57706180/generict-base-class-how-to-get-type-of-t-from-within-instance 再来简单分析下源码。 talk is cheap, show me the code. from typing import Dict Dict[str, int]Dict只是一个类型,并不…...

Shell语法基础总结
Shell 变量使用变量只读变量删除变量变量类型Shell 字符串单引号与双引号字符串获取字符串长度提取子字符串拼接字符串Shell 数组定义数组读取数组获取数组的长度Shell 传递参数Shell 基本运算符算术运算符关系运算符布尔运算符逻辑运算符字符串运算符Shell 信息输出命令Shell …...
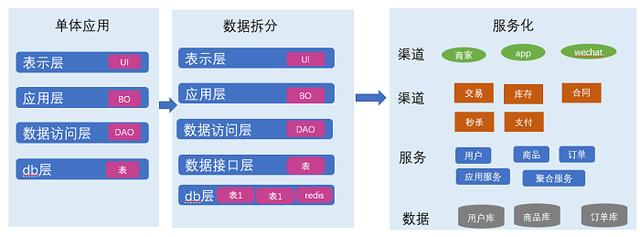
架构基本概念和架构本质
什么是架构和架构本质 在软件行业,对于什么是架构,都有很多的争论,每个人都有自己的理解。此君说的架构和彼君理解的架构未必是一回事。因此我们在讨论架构之前,我们先讨论架构的概念定义,概念是人认识这个世界的基础&…...

taobao.trade.ordersku.update( 更新交易的销售属性 )
¥开放平台免费API必须用户授权 只能更新发货前子订单的销售属性 只能更新价格相同的销售属性。对于拍下减库存的交易会同步更新销售属性的库存量。对于旺店的交易,要使用商品扩展信息中的SKU价格来比较。 必须使用sku_id或sku_props中的一个参数来更新&a…...
(附python代码实现))
算法实战应用案例精讲-【图像处理】使用scikit-image做图像处理(最终篇)(附python代码实现)
目录 高级滤波 autolevel bottomhat 与 tophat enhance_contrast entropy equalize gradient 其它滤波器...

数据结构与算法(四):树结构
前面讲到的顺序表、栈和队列都是一对一的线性结构,这节讲一对多的线性结构——树。「一对多」就是指一个元素只能有一个前驱,但可以有多个后继。 一、基本概念 树(tree)是n(n>0)个结点的有穷集。n0时称…...
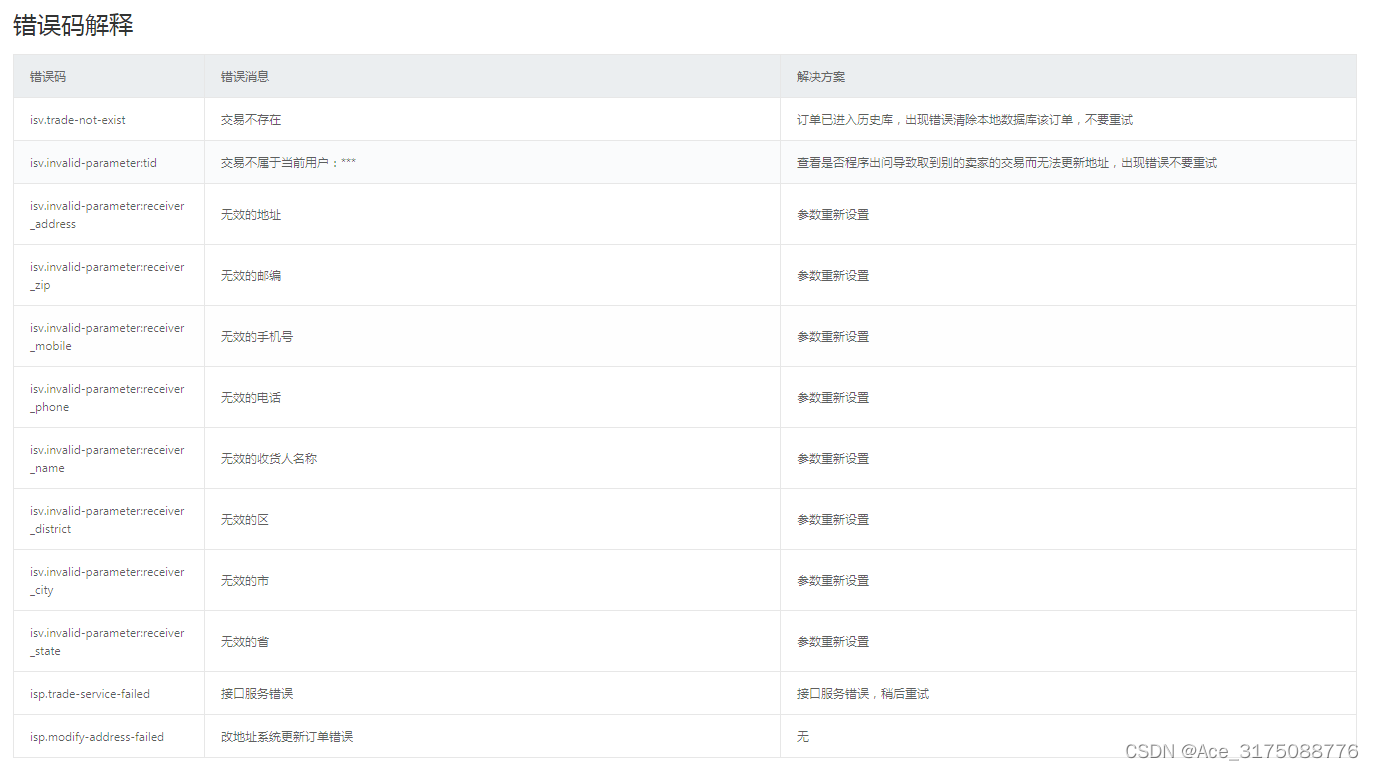
taobao.trade.shippingaddress.update( 更改交易的收货地址 )
¥开放平台免费API必须用户授权 只能更新一笔交易里面的买家收货地址 只能更新发货前(即买家已付款,等待卖家发货状态)的交易的买家收货地址 更新后的发货地址可以通过taobao.trade.fullinfo.get查到 参数中所说的字节为GBK编码的&…...
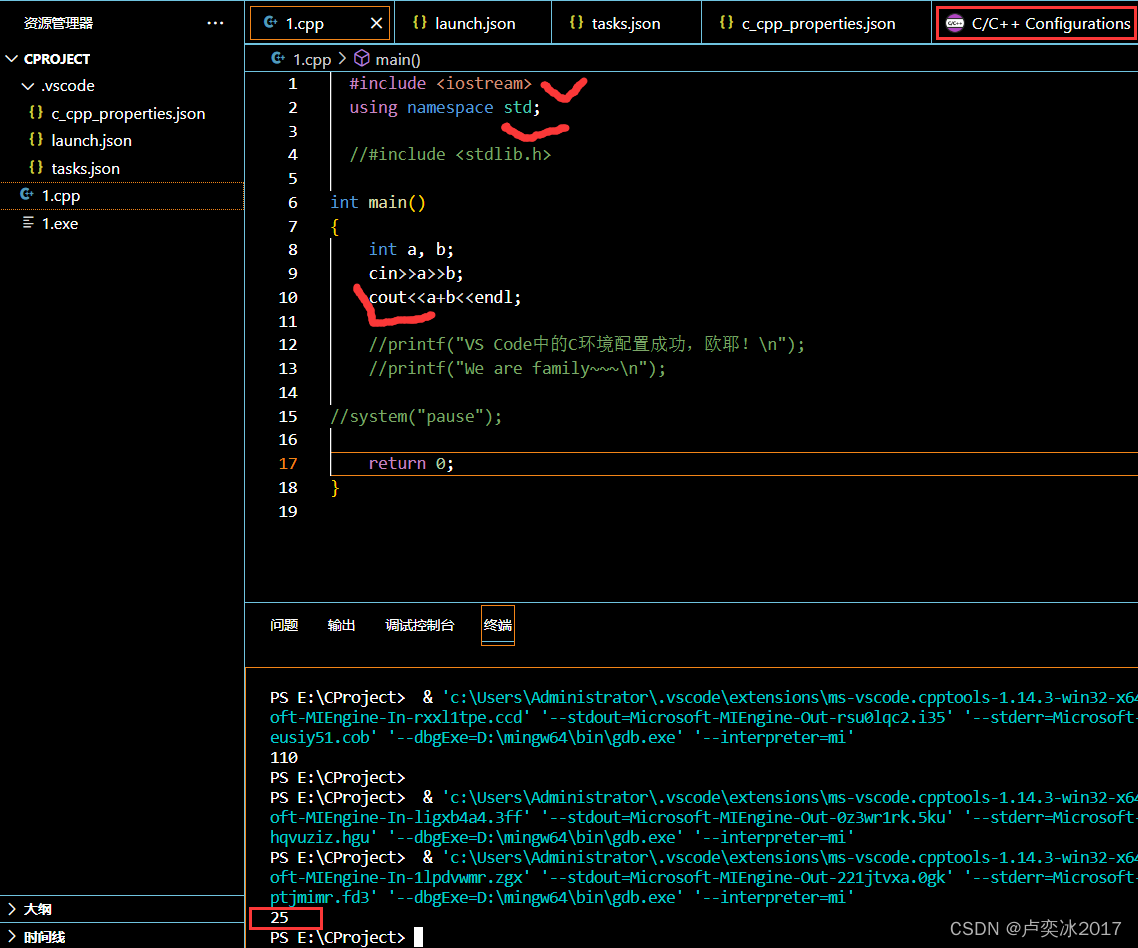
VS Code安装及(C/C++)环境配置(Windows系统)
参考资料2份: 从零开始的vscode安装及环境配置教程(C/C)(Windows系统)_光中影zone的博客-CSDN博客_vscode运行配置https://blog.csdn.net/qq_45807140/article/details/112862592 VSCode配置C/C环境 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/87864677 五…...
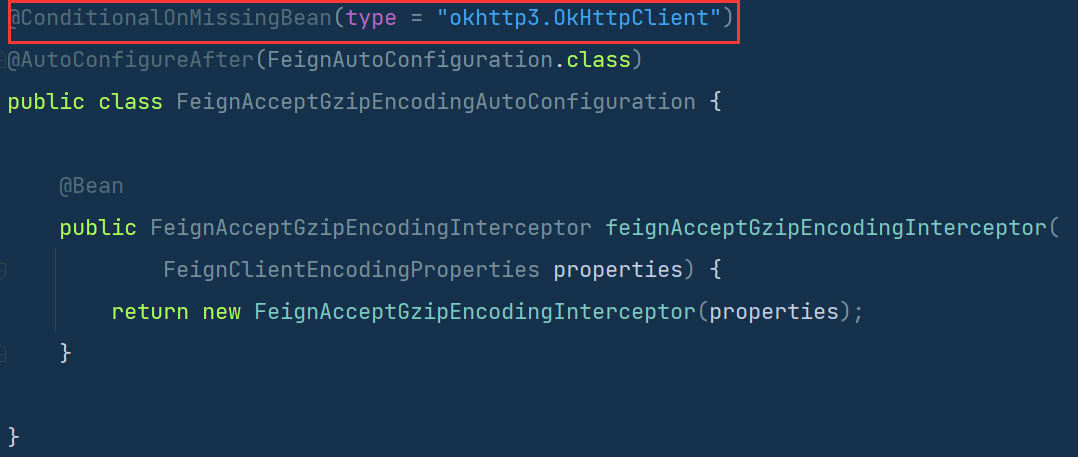
【Spring Cloud Alibaba】006-OpenFeign
【Spring Cloud Alibaba】006-OpenFeign 文章目录【Spring Cloud Alibaba】006-OpenFeign一、概述1、Java 项目实现接口调用的方法HttpclientOkhttpHttpURLConnectionRestTemplate WebClient2、Feign 概述二、Spring Cloud Alibaba 快速整合 OpenFeign1、添加依赖2、启动类加注…...

挚文集团短期内不适合投资,长期内看好
来源:猛兽财经 作者:猛兽财经 挚文集团(MOMO)在新闻稿中称自己是“中国在线社交和娱乐领域的领军企业”。 该公司旗下的陌陌是中国“陌生人社交网络”移动应用类别的领导者,并在2022年9月拥有超过1亿的月活跃用户。探…...

clion开发的常用快捷键以及gitcrlf的问题
前段报错:git config core.autocrlf false 然后删除app目录下的文件,除了.git文件夹然后 git bash ,执行 git reset --hardclion常用快捷键:Double shift 搜索文件F9调试F9运行到断点Ctrl F8 打断点F7单步步入Shift F8 单步跳出F8执行下一行代…...

LeetCode 格雷编码问题
格雷编码格雷编码的定义格雷编码的码表LeetCode 89. 格雷编码实例思路与代码思路一:找规律代码一代码二思路二:与自然数之间的关系(你必须知道,这个规律要去百度才知道)代码一LeetCode 1238. 循环码排列实例思路与代码…...

java生成html文件输出到指定位置
String fileName "filename.html";StringBuilder sb new StringBuilder();// 使用StringBuilder 构建HTML文件sb.append("<html>\n");sb.append("<head>\n");sb.append("<title>HTML File</title>\n");sb.a…...

华为OD机试用Python实现 -【微服务的集成测试】(2023-Q1 新题)
华为OD机试300题大纲 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 华为OD详细说明:https://dream.blog.csdn.net/article/details/128980730 微服务的集成测试…...
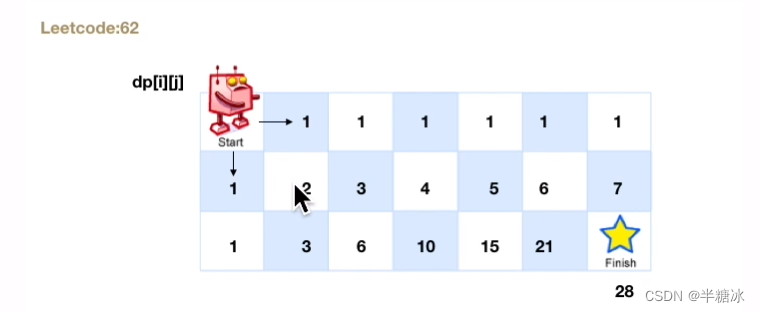
js版 力扣 62. 不同路径
一、题目描述 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。问总共有多少条不同的路径࿱…...

Qt音视频开发16-通用悬浮按钮工具栏的设计
一、前言 通用悬浮按钮工具栏这个功能经过了好几个版本的迭代,一开始设计的时候是写在视频控件widget窗体中,当时功能简单就放一排按钮在顶部悬浮widget中就好,随着用户需求的变化,用户需要自定义悬浮条的要求越发强烈࿰…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...