为什么曲面函数的偏导数可以表示其曲面的法向量?
为什么曲面函数的偏导数可以表示其曲面的法向量?
引用资料:
1.知乎@shinbade:曲面的三个偏导数为什么能表示法向量?
2.Geogebra@羅驥韡 (Pegasus Roe):偏導數、切平面、梯度
曲面 F ( x , y , z ) = 0 F(x,y,z)=0 F(x,y,z)=0,曲面上一点A ( x , y , z ) (x,y,z) (x,y,z),在该点附近取另一点B ( x + Δ x , y + Δ y , z + Δ z ) (x+\Delta x,y+\Delta y,z+\Delta z) (x+Δx,y+Δy,z+Δz),由于点B也在曲面上,故 F ( x + Δ x , y + Δ y , z + Δ z ) = 0 F(x+\Delta x,y+\Delta y,z+\Delta z)=0 F(x+Δx,y+Δy,z+Δz)=0,
将上式进行一阶泰勒展开:(一阶展开目的是用切平面上的点近似曲面上的点)
F ( x + Δ x , y + Δ y , z + Δ z ) = F ( x , y , z ) + F x ′ Δ x + F y ′ Δ y + F z ′ Δ z = 0 ∵ F ( x , y , z ) = 0 ∴ F x ′ Δ x + F y ′ Δ y + F z ′ Δ z = 0 ( F x ′ , F y ′ , F z ′ ) ⋅ ( Δ x , Δ y , Δ z ) = 0 F(x+\Delta x,y+\Delta y,z+\Delta z)=F(x,y,z)+F'_x\Delta x+F'_y\Delta y+F'_z\Delta z=0\\ ~\\ \because F(x,y,z)=0\\ ~\\ \therefore F'_x\Delta x+F'_y\Delta y+F'_z\Delta z=0\\ ~\\ (F'_x,F'_y,F'_z)\cdot(\Delta x,\Delta y,\Delta z)=0 F(x+Δx,y+Δy,z+Δz)=F(x,y,z)+Fx′Δx+Fy′Δy+Fz′Δz=0 ∵F(x,y,z)=0 ∴Fx′Δx+Fy′Δy+Fz′Δz=0 (Fx′,Fy′,Fz′)⋅(Δx,Δy,Δz)=0
向量 ( Δ x , Δ y , Δ z ) (\Delta x,\Delta y,\Delta z) (Δx,Δy,Δz)与向量 ( F x ′ , F y ′ , F z ′ ) (F'_x,F'_y,F'_z) (Fx′,Fy′,Fz′)内积为0,说明两向量垂直,又由于向量 ( Δ x , Δ y , Δ z ) (\Delta x,\Delta y,\Delta z) (Δx,Δy,Δz)在切平面上(严格来说是割平面,因为还没有取极限),故向量 ( F x ′ , F y ′ , F z ′ ) (F'_x,F'_y,F'_z) (Fx′,Fy′,Fz′)垂直于切平面,也就可以用其来表示曲面的法向量。
备注:切平面上点代替曲面上点(以直代曲),这个方面的理解详见本人博客:如何理解二元函数的可导与可微?
由于在极限过程中,切平面上点无限接近曲面上的点,所以近似将向量 ( Δ x , Δ y , Δ z ) (\Delta x,\Delta y,\Delta z) (Δx,Δy,Δz)看作在切片面上。




相关文章:

为什么曲面函数的偏导数可以表示其曲面的法向量?
为什么曲面函数的偏导数可以表示其曲面的法向量? 引用资料: 1.知乎shinbade:曲面的三个偏导数为什么能表示法向量? 2.Geogebra羅驥韡 (Pegasus Roe):偏導數、切平面、梯度 曲面 F ( x , y , z ) 0 F(x,y,z)0 F(x,y,…...

❤Uniapp报npx update-browserslist-db@latest
❤ Uniapp报npx update-browserslist-dblatest 按照提示先更新一下 npx update-browserslist-dblatest然后打开一下端口...
【C++】静态成员函数 ( 静态成员函数概念 | 静态成员函数声明 | 静态成员函数访问 | 静态成员函数只能访问静态成员 )
文章目录 一、静态成员函数简介1、静态成员函数概念2、静态成员函数声明3、静态成员函数访问4、静态成员函数只能访问静态成员 二、代码示例 - 静态成员函数 一、静态成员函数简介 1、静态成员函数概念 静态成员函数归属 : 在 C 类中 , 静态成员函数 是一种 特殊的函数 , 该函数…...
)
基于若依ruoyi-nbcio增加flowable流程待办消息的提醒,并提供右上角的红字数字提醒(三)
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 1、上一节说到RedisReceiver ,这里有调用了NbcioRedisListener自定义业务监听,如下…...

用友第五届开发者大赛初赛晋级公示,复赛火热进行中!
用友第五届开发者大赛初赛晋级公示,复赛火热进行中! 自7月13日鸣锣揭幕,9月6日各赛道作品初评工作完成,历时近两月,用友第五届企业云服务开发者大赛初赛阶段顺利落下帷幕。作为备受各界开发者关注的赛事,本…...

SSL证书如何做到保障网站安全?
当网站显示不安全时,用户会在头脑中产生该网站是否合法的疑问,如果是购物网站或者购物商城,那意味着可能会损失大部分的用户。而SSL证书能有效保障网站的安全性,轻松解决网站不被用户信任的问题。那么,SSL证书究竟是如…...
C# Onnx Yolov8 Detect Poker 扑克牌识别
效果 项目 代码 using Microsoft.ML.OnnxRuntime; using Microsoft.ML.OnnxRuntime.Tensors; using OpenCvSharp; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System…...

想要精通算法和SQL的成长之路 - 最长等差数列
想要精通算法和SQL的成长之路 - 最长等差数列 前言一. 最长等差数列 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 最长等差数列 原题链接 思路: 我们假设dp[i][j] 为:以num[i]为结尾,以j为公差的最长等差子序列的长度。由此可知&a…...

【简单的自动曝光】python实现-附ChatGPT解析
1.题目 一个图像有 n 个像素点,存储在一个长度为 n 的数组 img 里, 每个像素点的取值范围[0,255] 的正整数。 请你给图像每个像素点值,加上一个整数 k (可以是负数),得到新图 newImg , 使得新图newImg 的所有像素平均值最接近中位值 128。 请输出这个整数 k。 输入描述 n …...

网工内推 | 运维工程师,CCNP认证优先,周末双休,多次调薪机会
01 驻场运维 职责描述: 1、驻场某大型汽车整车厂,配合客户完成网络相关(路由交换)的项目。 2、按照客户要求,与项目组配合共同完成项目前期调研,设计,规划,项目中期调试测试&#…...

LeetCode 1337. The K Weakest Rows in a Matrix【数组,二分,堆,快速选择,排序】1224
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

如何使用Spring提供的Retry
0、本例中使用的是 springboot-2.0.4.RELEASE,jdk1.8 1、导包。需要注意版本。2.0.0需要spring6和jdk17 <dependency><groupId>org.springframework.retry</groupId><artifactId>spring-retry</artifactId><version>1.3.4<…...
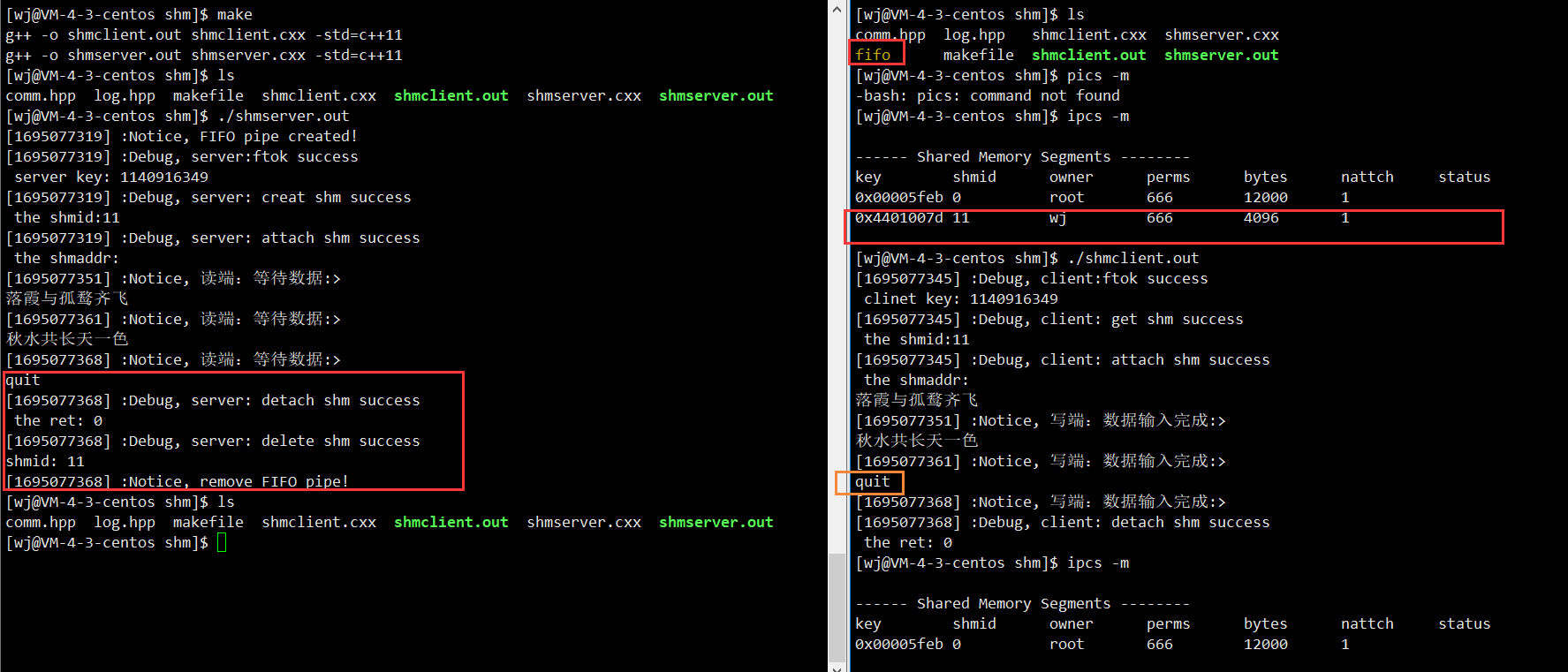
【ONE·Linux || 进程间通信】
总言 进程间通信:简述进程间通信,介绍一些通信方式,管道通信(匿名、名命)、共享内存等。 文章目录 总言1、进程间通信简述2、管道2.1、简介2.2、匿名管道2.2.1、匿名管道的原理2.2.2、编码理解:用fork来共…...
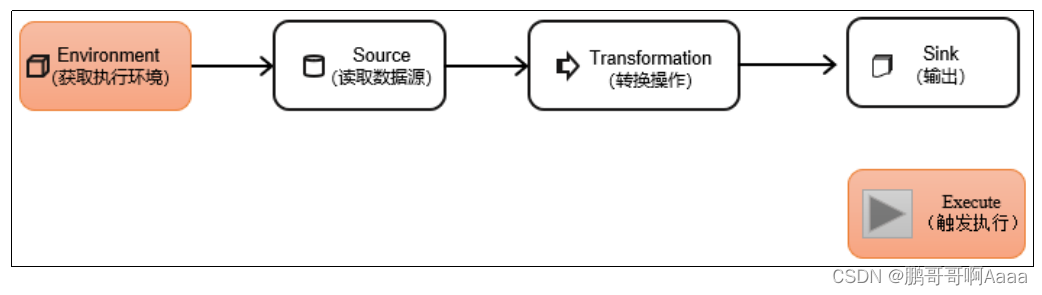
207.Flink(二):架构及核心概念,flink从各种数据源读取数据,各种算子转化数据,将数据推送到各数据源
一、Flink架构及核心概念 1.系统架构 JobMaster是JobManager中最核心的组件,负责处理单独的作业(Job)。一个job对应一个jobManager 2.并行度 (1)并行度(Parallelism)概念 一个特定算子的子任务(subtask)的个数被称之为其并行度(parallelism)。这样,包含并行子任…...
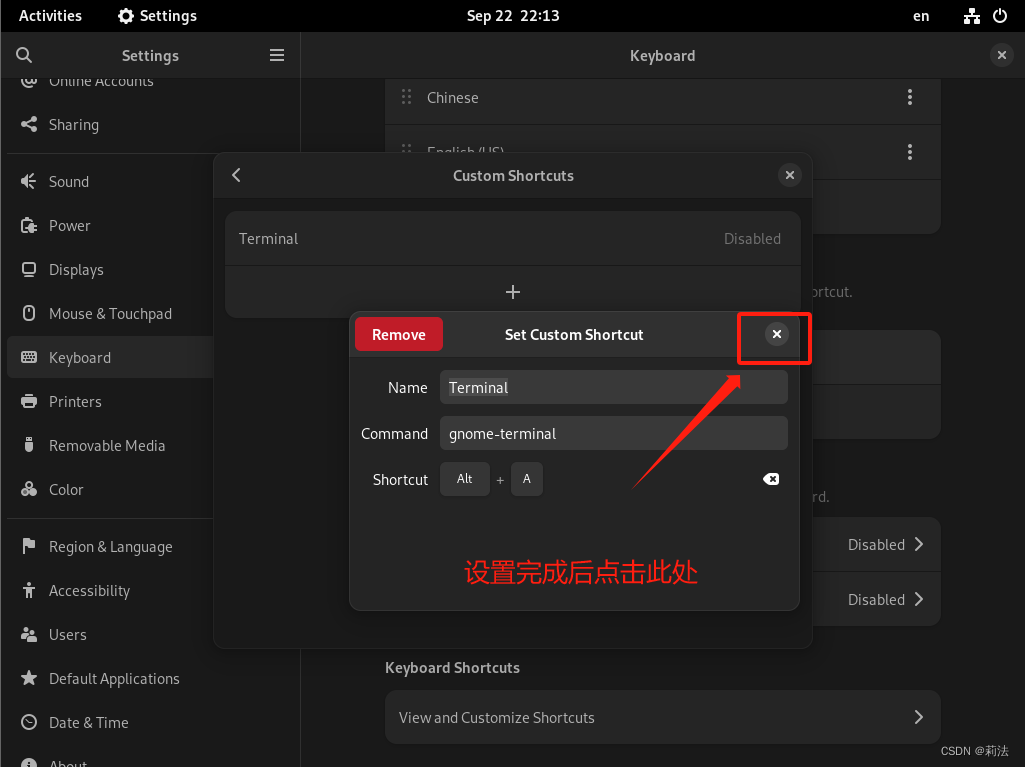
debian终端快捷键设置
为了方便使用图形化debian,快捷调出shell终端是提升工作学习效率的最重要的一步。 1.首先点击右上角,选择设置 2.点击键盘,选择快捷键,并创建自定义快捷键 3.点击添加快捷键 4.根据图中提示创建快捷键 Name: Terminal Command…...

原生ajax
什么是Ajax Asynchronous JavaScript and xml 异步的 js 和 xml(数据承载方式) ,本质:使用js提供的异步对象XMLHttpRequest 异步的向服务器提交请求,并且接受服务器响应回来的数据。 使用ajax 1.创建异步对象 var xhrnew XMLHttp…...
:并发编程)
面试题库(五):并发编程
多线程类的使用 java线程同步有哪些方法、各自的优缺点synchronized 和ReentrantLock区别,可重入锁是什么?threadlocal有什么用Java中创建线程有几种方式?分别是? 当主线程执行结束后,子线程还会继续执行下去吗?JUC中有哪些常用的集合?(项目中用到的)CopyOnWriteArray…...

Android FileProvider笔记
一、FileProvider是什么 通过FileProvider.getUriForFile(NonNull Context context, NonNull String authority, NonNull File file)方法获得一个有临时权限的Uri给客户端用来访问本APP文件。 当然看FileProvider类的注释更加详细 二、代码示例 <providerandroid:name&q…...
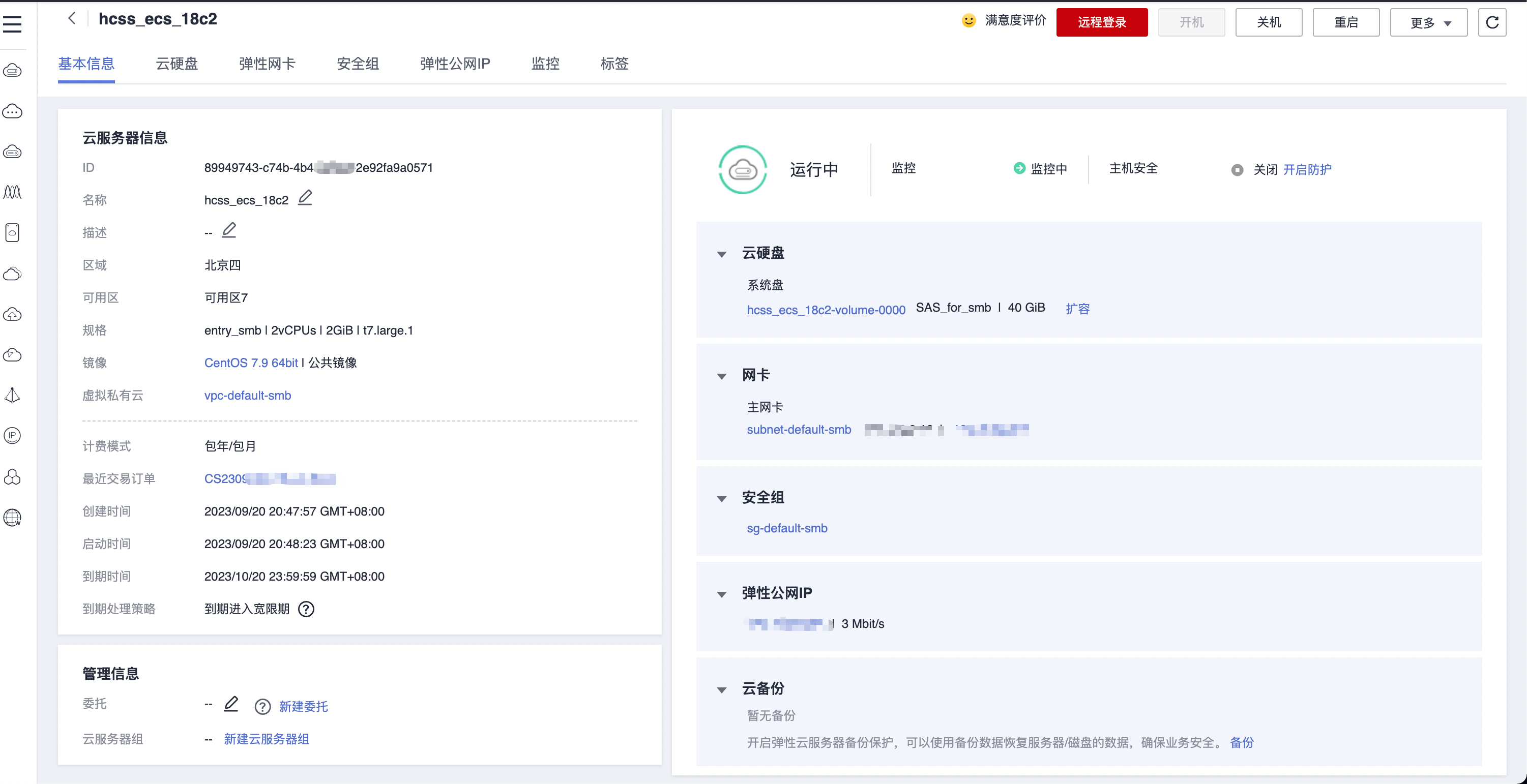
华为云云耀云服务器L实例评测 |云服务器选购
华为云耀云服务器 L 实例是一款轻量级云服务器,开通选择实例即可立刻使用,不需要用户再对服务器进行基础配置。新用户还有专享优惠,2 核心 2G 内存 3M 带宽的服务器只要 89 元/年,可以点击华为云云耀云服务器 L 实例购买地址去购买…...

2023-09-22 LeetCode每日一题(将钱分给最多的儿童)
2023-09-22每日一题 一、题目编号 2591. 将钱分给最多的儿童二、题目链接 点击跳转到题目位置 三、题目描述 给你一个整数 money ,表示你总共有的钱数(单位为美元)和另一个整数 children ,表示你要将钱分配给多少个儿童。 你…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...
