【二叉树魔法:链式结构与递归的纠缠】
本章重点
- 二叉树的链式存储
- 二叉树链式结构的实现
- 二叉树的遍历
- 二叉树的节点个数以及高度
- 二叉树的创建和销毁
- 二叉树的优先遍历和广度优先遍历
- 二叉树基础oj练习
1.二叉树的链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所 在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面学到高阶数据结构如红黑树等会用到三叉链。

typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* left; // 指向当前节点左孩子struct BinTreeNode* right; // 指向当前节点右孩子BTDataType data; // 当前节点值域
};// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* parent; // 指向当前节点的双亲struct BinTreeNode* left; // 指向当前节点左孩子struct BinTreeNode* right; // 指向当前节点右孩子BTDataType data; // 当前节点值域
};2.二叉树链式结构的实现
这里我们就不讲解二叉树链式结构的增删查改,因为二叉树链式结构的增删查改没有意义,其链式二叉树形式复杂,数据增删查改消耗较大。
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在对二叉树结构掌握还不够深入,为了降低学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
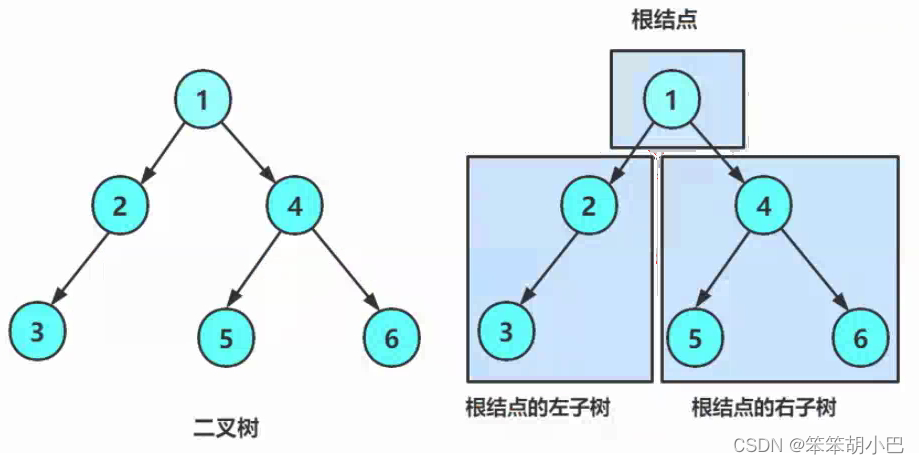
下面我们根据上图手动去构建一个二叉树链式的结构。
#include <stdio.h>
#include <stdlib.h>typedef int BTDataType;
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;BTDataType data;
}BTNode;BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");exit(-1);}node->data = x;node->left = node->right = NULL;return node;
}int main()
{//手动构建二叉树BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return 0;
}3.二叉树的遍历
3.1前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉 树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。

按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前(依次访问:跟 左子树 右子树)。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)(依次访问:左子树 跟 右子树)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后(依次访问:左子树 右子树 跟)。
根据上面的图得出:
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
再看二叉树基本操作前,再回顾下二叉树的概念,二叉树是:
- 空树
- 非空:根节点,根节点的左子树、根节点的右子树组成的。

前序遍历结果:1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL
中序遍历结果: NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL
后序遍历结果: NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1
从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
// 二叉树前序遍历
void PreOrder(BTNode* root);
// 二叉树中序遍历
void InOrder(BTNode* root);
// 二叉树后序遍历
void PostOrder(BTNode* root);
3.1.1、二叉树前序遍历:void PreOrder(BTNode * root);
// 二叉树前序遍历
void PreOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}运行结果:

递归图:

3.1.2、二叉树中序遍历:void InOrder(BTNode* root);
// 二叉树中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}运行结果:
3.1.3、二叉树后序遍历:void PostOrder(BTNode* root);
// 二叉树后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}运行结果:

3.2层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层 上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。

我们该如何层序遍历一颗树呢?这里我们还能用递归嘛?不行,层序遍历没有先访问左子树和右子树的关系,层序遍历是一层一层访问的,递归的思想不符合层序遍历,这里我们可以使用队列,先把根节点入队列,然后当根节点出队列的时候,再把根节点的左右孩子入队列,特点是上一层带下一层,由于队列是先进先出的特点,刚好符合层序遍历。
这里需要注意一个问题,我们存储队列的数据是链式树中的data嘛,这样并不行,我们如果存放值进去,就找不到左右孩子的值了,所以我们需要存储结构体,但是二叉树结构体所占空间大,因此我们传入二叉树结构体的地址进去。
//Queue.h中需要修改QDataType
typedef struct BinaryTreeNode* QDataType;#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>typedef int BTDataType;
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;BTDataType data;
}BTNode;#include "Queue.h"// 层序遍历
void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if(root != NULL)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);printf("%d ", front->data);if(front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);QueuePop(&q);}QueueDestroy(&q);
}
BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");exit(-1);}node->data = x;node->left = node->right = NULL;return node;
}
int main()
{//手动构建二叉树BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;LevelOrder(node1);return 0;
}运行结果:

4.二叉树的节点个数以及高度
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);4.1二叉树节点个数:int BinaryTreeSize(BTNode* root);
求二叉树节点的个数我们最容易想到的就是遍历二叉树,然后遇到一个不为NULL的节点就加,但是我们本章主要是使用递归的思想,所有都采用递归的思想去解题。
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{int size = 0;if (root == NULL)return 0;elsesize++;BinaryTreeSize(root->left);BinaryTreeSize(root->right);
}我们首先看看上面的写法有什么错误,很明显,上面犯了一个很严重的错误,返回局部变量的值,我们知道,函数内创建的局部变量在函数释放时候,其空间会被销毁,那么上面的size就会得到一个随机值。
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{static int size = 0;//静态变量,生命周期边长if (root == NULL)return 0;elsesize++;BinaryTreeSize(root->left);BinaryTreeSize(root->right);return size;
}再看看上面的代码,我们将size用static修饰,那么此时size就会存放在静态区,此时size生命周期就会变长,但是在函数内部我们有一个给size初始化为0的语句,这样会不会在每次函数调用的时候都会初始化为0呢?不会,局部的静态变量初始化只会被执行一次。我们调试发现,当再次进入函数时,给size初始化为0的语句直接被跳过了。

运行结果:

我们可以看到结果求出来了,也确实是正确的,但是我们可以发现,静态变量的size生命周期是和程序的生命周期相同的,如果我们后面再次调用函数,size会从上一次的基础上加上去,比如我们再调用一次函数,结果是:
所以我们上面的函数是一次性的,只能使用一次,不方便,不过也有方法解决,我们此时就不用静态变量了,我们将size设置为全局变量,然后在每次调用的时候,手动将size的值赋值为0,但是这样不够优雅,下面我们来介绍一下递归方法。
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}递归图
这样结果就出来啦!!!
4.2二叉树叶子节点个数:int BinaryTreeLeafSize(BTNode* root)
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}递归图:

4.3二叉树第k层节点个数:int BinaryTreeLevelKSize(BTNode* root, int k)
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k > 0);if (root == NULL)return 0; if (k == 1)return 1;return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}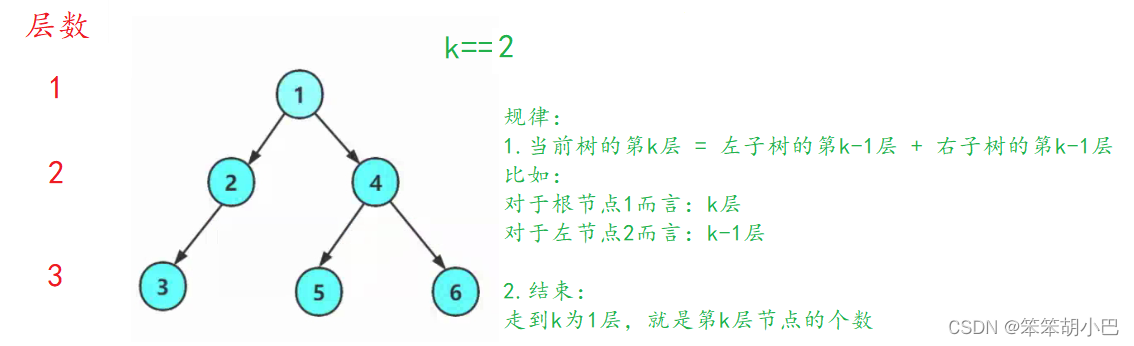
递归图

4.4二叉树查找值为x的节点:BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
我们首先拿到这个题目,就可以确定我们是从根节点开始查找,然后再左子树,右子树查找,很明显的前序遍历,因此我们可以按照前序遍历的思路查找该值。、
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;BinaryTreeFind(root->left, x);BinaryTreeFind(root->right, x);
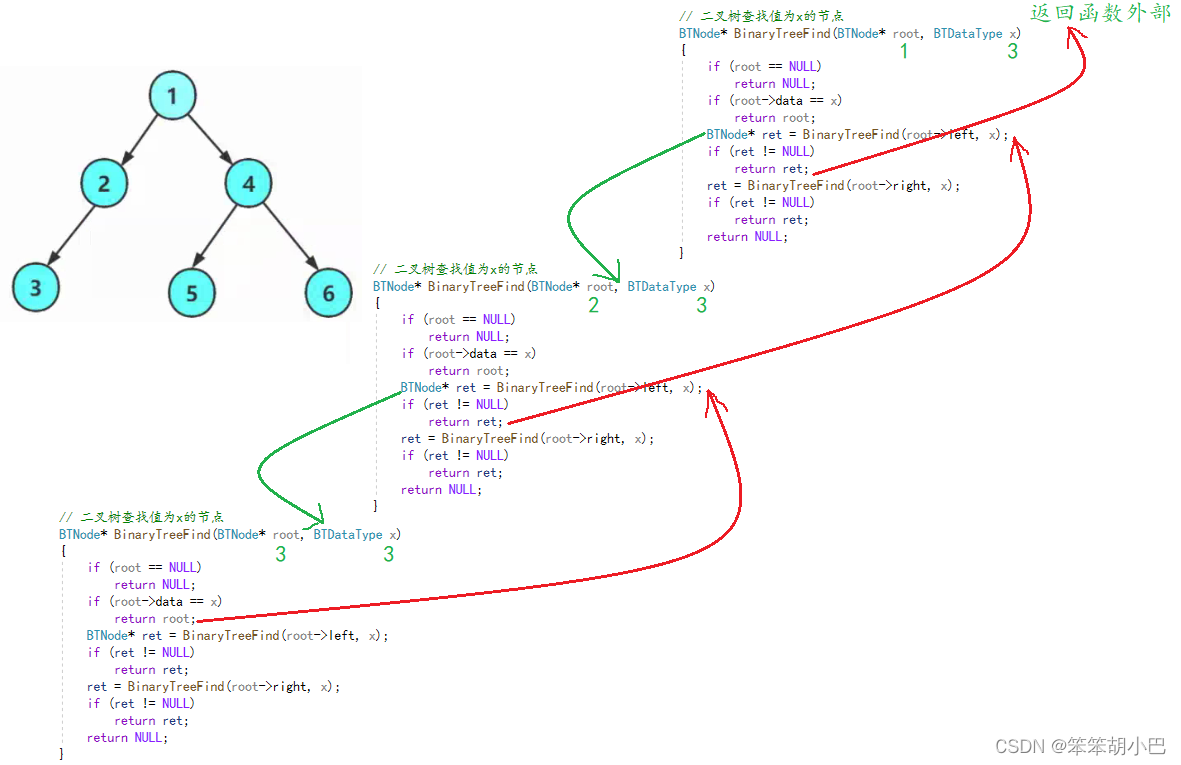
}我们看看上面的代码有问题嘛?很明显画个递归图就可以观察到问题。

很明显,我们找到值相等的节点,但是返回值并不是直接返回到最外面,而是返回给上一层函数,但是上一层函数又没有接收该返回值,返回值就被扔掉了,本来该值已经找到了,又再去递归右树,所以上面的写法是错误的。
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;return BinaryTreeFind(root->left, x) || BinaryTreeFind(root->right, x);
}上面的这种写法避免了再去递归右树的问题,但是逻辑或运算符的返回结果是真假,不符合返回指针要求。根据上面的错误,首先要确定能够有返回值返回,其次是左子树找到了就不要去右子树找了。
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;BTNode* ret = BinaryTreeFind(root->left, x);if (ret != NULL)return ret;ret = BinaryTreeFind(root->right, x);if (ret != NULL)return ret;return NULL;
}递归图:
4.5二叉树的高度int TreeHeight(BTNode* root)
二叉树的高度怎么求呢?我们可以尝试一下递归的思路,我们可以先求左子树的高度,然后再求右子树的高度,比较两棵子树谁的高度大,返回高度大的那棵子树并加上根节点就是整棵树的高度
//二叉树的高度
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;return TreeHeight(root->left) > TreeHeight(root->right) ? TreeHeight(root->left) + 1: TreeHeight(root->right) + 1;
}我们将上面的代码去力扣上编译一下:链接

但是我们发现上面的程序超出时间限制,为什么呢?我们发现我们的程序先递归一遍求左子树和右子树的高度,然后选出那个较大,并没有保存高度,仅仅只是比较,执行完三目操作符的比较后,假设左子树经过比较高度大,后面的对左子树的高度又要递归一次,所以上面的代码求解高度需要先递归左数,再递归右数,然后比较,再将高度大的那颗树再去递归求高度。我们可以通过保存第一次递归时的高度就可以啦
int maxDepth(struct TreeNode* root){if (root == NULL)return 0;int leftHeight = maxDepth(root->left);int rightHeight = maxDepth(root->right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}但是上面定了变量,那有没有不定义变量的方法呢?我们可以利用函数传参的特点。

int TreeHeight(BTNode* root)
{if (root == NULL)return 0;return fmax(TreeHeight(root->left), TreeHeight(root->right)) + 1;
}通过fmax函数,我们将第一次递归的左子树和右子树高度传入形参中,传参是将求下来的结果放到形参中,这样也就间接保存了左子树和右子树高度。
5.二叉树的创建和销毁
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);
5.1通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树:BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
由于二叉树的前序遍历是先访问根节点,在访问左子树,最后访问右子树,所以当第一次访问的到#时,该二叉树的左子树就访问完了,就要开始访问右子树了。
#include <stdio.h>
#include <stdlib.h>
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;char data;
}BTNode;BTNode* BinaryTreeCreate(char* str, int* pi)
{if (str[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL){perror("malloc fail");exit(-1);}root->data = str[*pi];(*pi)++;//左数构建完自然到右树root->left = BinaryTreeCreate(str, pi);root->right = BinaryTreeCreate(str, pi);return root;
}
// 二叉树前序遍历
void PreOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}printf("%c ", root->data);PreOrder(root->left);PreOrder(root->right);
}
int main()
{char str[100];scanf("%s", str);int i = 0;BTNode* root = BinaryTreeCreate(str, &i);PreOrder(root);return 0;
}递归图:

前序遍历:

5.2二叉树销毁:void BinaryTreeDestory(BTNode** root);
// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{if (root == NULL)return;BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);root == NULL;
}我们看看上面的代码有问题嘛,最后一步的root置空有问题,因为root是形参,形参的改变是不会改变实参的,所以上面是root置空没有效果,可以使用二级指针通过地址去修改实参,或者我们可以在函数调用完后手动加一个置空。
// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{if (root == NULL)return;BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);
}5.3判断二叉树是否是完全二叉树:int BinaryTreeComplete(BTNode* root);

我们首先看看完全二叉树的特点:前h-1层的节点个数都是满的,最后一层的个数可能是满的。那我们是不是可以先求二叉树的高度,然后再去求每层节点的个数是否符合h层的节点个数呢?我们来看看下面一个图。
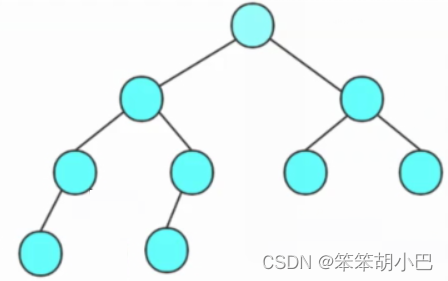
很明显,前h-1层是符合的,但是最后一层呢?完全二叉树的最后一层节点是一个范围值,比如上图,h层的节点个数是符号最后一层节点数量范围的,但是上面是完全二叉树嘛?很明显,不是,所以上面的思路是错误的。所以要换一个思路,我们发现完全二叉树的层序遍历非空节点是连续的。那我们是不是可以利用这一点去判断一棵树是不是完全二叉树。但是我们要改变一下层序遍历的代码,将空节点也入进队列去。
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root != NULL)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);if (front == NULL)break;QueuePush(&q, front->left);QueuePush(&q, front->right);QueuePop(&q);}//已经遇到空节点,如果队列中还有后面的节点非空,就不是完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){QueueDestroy(&q);return 0;}}QueueDestroy(&q);return 1;
}上面我们需要注意一点,BTNode* front = QueueFront(&q);取到队头节点之后我们就执行QueuePop(&q);那我们后面还能访问front节点嘛?可以,因为pop是删除队列的节点,不是删除树的节点。
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为( )
A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA
解析:题目上告知我们该树是完全二叉树,那么每一层有
个节点,所以该树则为:
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
A E
B F
C G
D H
解析:先序遍历为EFHIGJK,先访问根节点,所以根节点为E
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为____。
A adbce
B decab
C debac
D abcde
解析:中序遍历是先访问左子树,根节点,再右子树,后序遍历是先访问左子树,右子树,根节点,所以可以确定a是根节点,b是左子树,dce是右子树,所以该树则为:
4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为
A FEDCBA
B CBAFED
C DEFCBA
D ABCDEF
解析:中序遍历是先访问左子树,根节点,再右子树,后序遍历是先访问左子树,右子树,根节点,所以可以确定F是根节点,层序是从根节点一层一层遍历,即可确定答案A
6.二叉树的优先遍历和广度优先遍历深度优先遍历和广度优先遍历
深度优先遍历(Depth-First Search,DFS)和广度优先遍历(Breadth-First Search,BFS)是两种常用的图遍历算法,用于在图或树数据结构中查找或遍历节点。
深度优先遍历 (DFS):前序
DFS 是一种递归或堆栈(栈)的遍历方法,其核心思想是从一个起始节点开始,沿着一条路径尽可能深地探索,直到无法再继续深入,然后回退到上一个节点,再继续探索其他路径。DFS 可以帮助我们找到图中的所有节点,并且可以用于解决许多与路径和连通性相关的问题。
DFS 的基本特点:
- 从起始节点开始遍历。
- 递归或使用栈来管理节点的访问顺序。
- 深度优先,先探索一个分支直到底部,然后再回溯探索其他分支。
DFS 在解决一些问题时可能会遇到无限深度的情况,为了避免这种情况,通常需要使用适当的条件来限制深度。
广度优先遍历 (BFS):层序
BFS 是一种层次遍历方法,从起始节点开始,首先访问起始节点,然后逐层地访问该节点的邻居节点,直到遍历完所有的节点或达到特定条件为止。BFS 常用于寻找最短路径或在图中查找特定节点。
BFS 的基本特点:
- 从起始节点开始遍历。
- 使用队列来管理节点的访问顺序。
- 广度优先,先访问当前节点的邻居节点,再访问邻居节点的邻居节点。
BFS 可以用于寻找最短路径,因为它会按层级逐步扩展,首次到达目标节点时即可确定为最短路径。
总结:
- DFS 主要用于深度探索,适用于寻找路径、连通性等问题。
- BFS 主要用于广度搜索,适用于寻找最短路径、层级遍历等问题。
7.二叉树基础oj练习
1. 单值二叉树。Oj链接
2. 检查两颗树是否相同。OJ链接
3. 对称二叉树。OJ链接
4. 二叉树的前序遍历。 OJ链接
5. 二叉树中序遍历 。OJ链接
6. 二叉树的后序遍历 。OJ链接
7. 另一颗树的子树。OJ链接

相关文章:

【二叉树魔法:链式结构与递归的纠缠】
本章重点 二叉树的链式存储二叉树链式结构的实现二叉树的遍历二叉树的节点个数以及高度二叉树的创建和销毁二叉树的优先遍历和广度优先遍历二叉树基础oj练习 1.二叉树的链式存储 二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑…...

FL Studio21.0.3最新中文版下载安装详解
安装第一步:卸载干净fl历史旧版本,彻底退出安全软件 (如果下载好的文件无法打开,可以去百度下载一个解压工具,比如bandzip、360压缩、2345好压...)(卸载直接用电脑管家卸载或者在左下角开始处找…...

【算法与数据结构】JavaScript实现十大排序算法(一)
文章目录 关于排序算法冒泡排序选择排序插入排序希尔排序归并排序 关于排序算法 稳定排序: 在排序过程中具有相同键值的元素,在排序之后仍然保持相对的原始顺序。意思就是说,现在有两个元素a和b,a排在b的前面,且ab&…...

IntelliJ IDEA使用——插件推荐
官网插件库:https://plugins.jetbrains.com/search 代码规范检测:Alibaba Java Coding Guidelines码云:Giteemybatis插件:MyBatisX多颜色括号:Rainbow Brackets操作快捷键提示:Key Promoter X力扣ÿ…...

编写一个会导致死锁的程序,将怎么解决?
死锁发生在两个或多个线程互相等待对方释放资源的情况下。下面是一个可能导致死锁的情况: public class DeadlockExample {private static final Object lock1 = new Object();private static final Object lock2 = new...
Java JVM分析利器JProfiler 结合IDEA使用详细教程
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、JProfiler是什么?二、我的环境三、安装步骤1.Idea安装JProfiler插件1.下载程序的安装包 四、启动 前言 对于我们Java程序员而言,肯…...
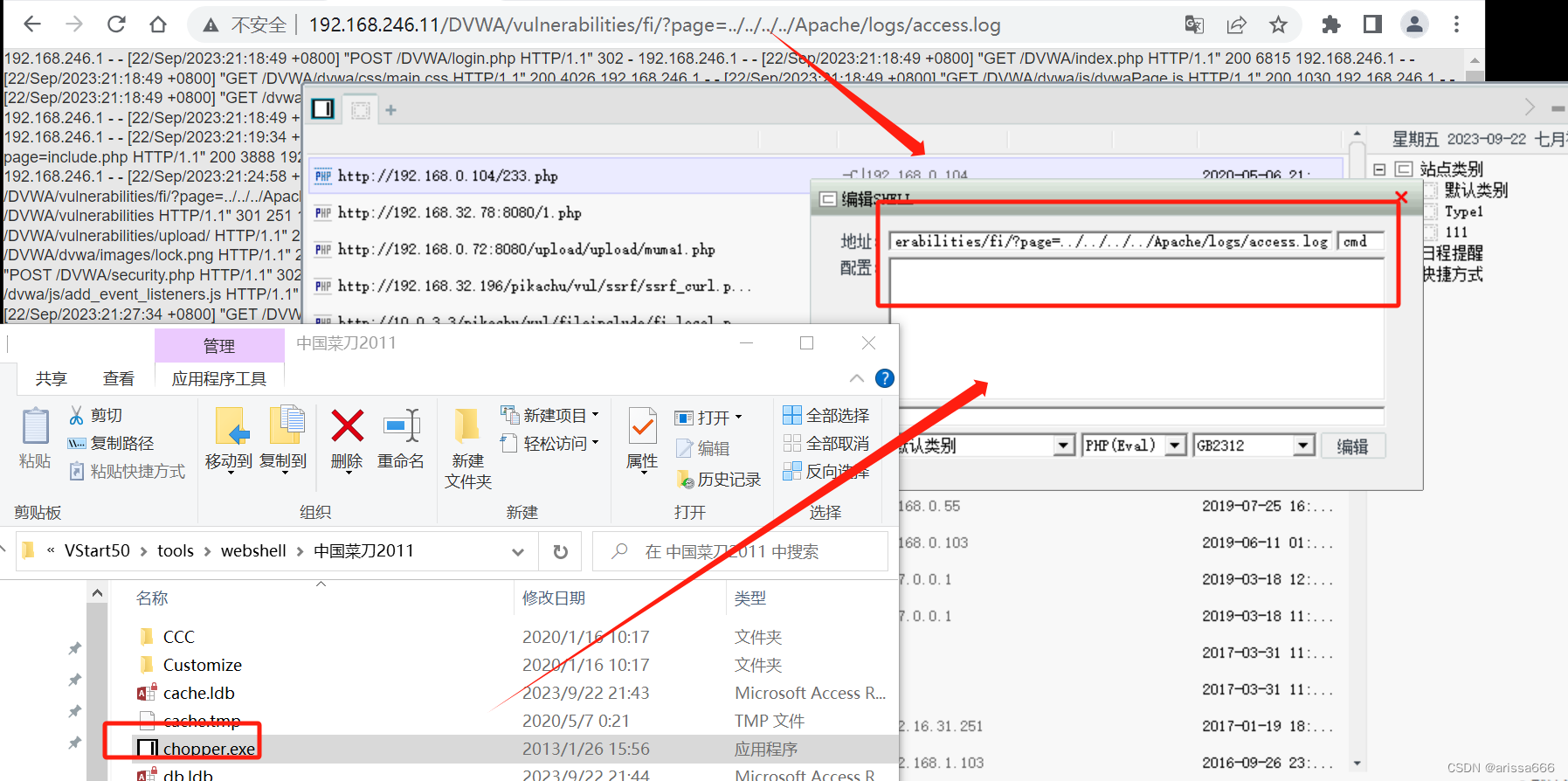
包含日志文件
原理:某个PHP文件存在本地包含漏洞,却无法上传正常文件,包含漏洞却不能利用,攻击者就有可能会利用apache日志文件来入侵。 Apache服务器运行后会生成两个日志文件,这两个文件是access.log(访问日志)和error.log(错误日…...

李航老师《统计学习方法》第2章阅读笔记
感知机(perceptron)时二类分类的线性分类模型,其输入为实例的特征向量,输出为实例的类别,取1和-1二值。感知机对应于输入空间(特征空间)中将实例划分为正负两类的分离超平面 想象一下在一个平面…...
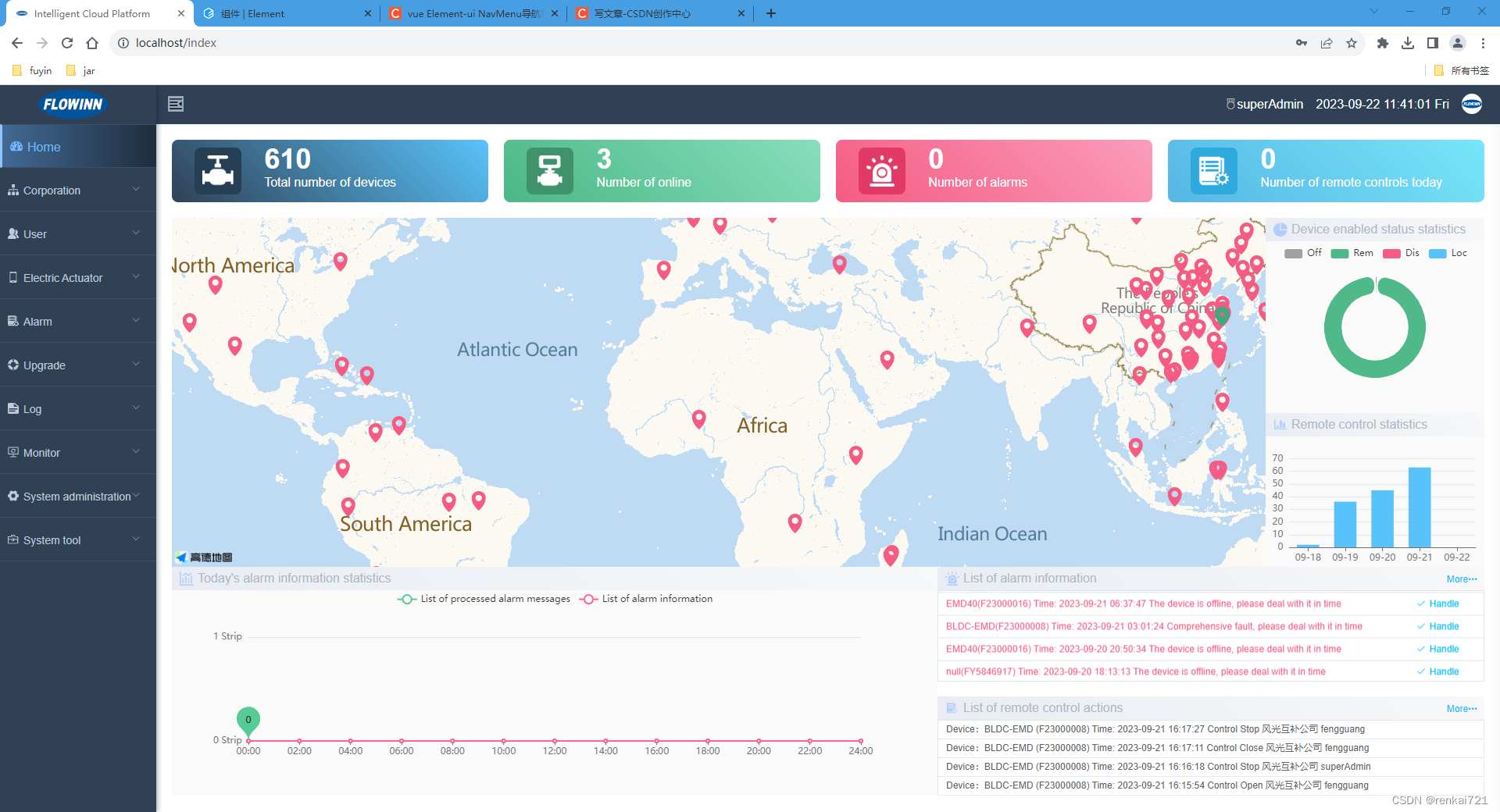
ruoyi框架修改左侧菜单样式
菜单效果 ruoyi前端框架左侧的菜单很丑,我们需要修改一下样式,下面直接看效果。 修改代码 1、sidebar.scss .el-menu-item, .el-submenu__title {overflow: hidden !important;text-overflow: ellipsis !important;white-space: nowrap !important;//…...

【已解决】PyCharm里的黄色波浪线
问题描述 有时候在PyCharm中某些代码下面会有黄色波浪线。 问题解释 黄色波浪线只是提示这段代码不规范,但对程序的运行并没有本质影响。...
)
设计模式:策略模式(C++实现)
策略模式(Strategy Pattern)是一种行为设计模式,它定义了一系列的算法,并将每个算法封装成独立的对象,使得它们可以互相替换。下面是一个使用C实现策略模式的示例: #include <iostream>// 抽象策略类…...

网络安全深入学习第二课——热门框架漏洞(RCE—Thinkphp5.0.23 代码执行)
文章目录 一、什么是框架?二、导致框架漏洞原因二、使用步骤三、ThinkPHP介绍四、Thinkphp框架特征五、Thinkphp5.0.23 远程代码执行1、漏洞影响范围2、漏洞成因 六、POC数据包Windows下的Linux下的 七、漏洞手工复现1、先Burp抓包,把抓到的请求包发送到…...

Pdf文件签名检查
如何检查pdf的签名 首先这里有一个已经签名的pdf文件,通过pdf软件可以看到文件的数字签名。 图1为签名后的文件,图2为签名后文件被篡改。 下面就是如何代码检查这里pdf文件的签名 1.引入依赖 <dependency><groupId>org.projectlombok<…...

web前端之float布局与flex布局
float布局 <style>.nav {overflow: hidden;background-color: #6adfd0; /* 导航栏背景颜色 */}.nav a {float: left;display: block;text-align: center;padding: 14px 16px;text-decoration: none;color: #000000; /* 导航栏文字颜色 */}.nav a:hover {background-col…...

expected ‘,’ after expression in R【R错误】
出现如下错误: 在红色叉的位置,会有提示“expected . after expression”,咋一看出现红色叉的位置没有任何的错误,怎么会出现错误呢? 解决办法: 寻找这个代码第一次出现红色叉的位置,看其是否…...

算法|图论 2
LeetCode 695- 岛屿的最大面积 题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目描述:给你一个大小为 m x n 的二进制矩阵 grid 。 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求…...

使用C#实现服务端与客户端的简陋聊天
服务端代码: using System; using System.Net.Sockets; using System.Net; using System.IO;//服务器程序 namespace CSharpStudy_09_21 {class Program{static void Main(string[] args){int port 8865;TcpClient tcpClient;//创建tcp对象IPAddress[] serverIp Dns.GetHost…...
生成式模型和判别式模型区别
目录 1.概念 2.定义 3.举例 (1)例子 A (2)例子 B 4.特点 5.优缺点 6.代表算法 1.概念 首先我们需要明确,两种不同的模型都用于监督学习任务中。监督学习的任务就是从数据中学习一个模型,并用…...

【kafka实战】03 SpringBoot使用kafka生产者和消费者示例
本节主要介绍用SpringBoot进行开发时,使用kafka进行生产和消费 一、引入依赖 <dependencies><dependency><groupId>org.springframework.kafka</groupId><artifactId>spring-kafka</artifactId></dependency><depen…...
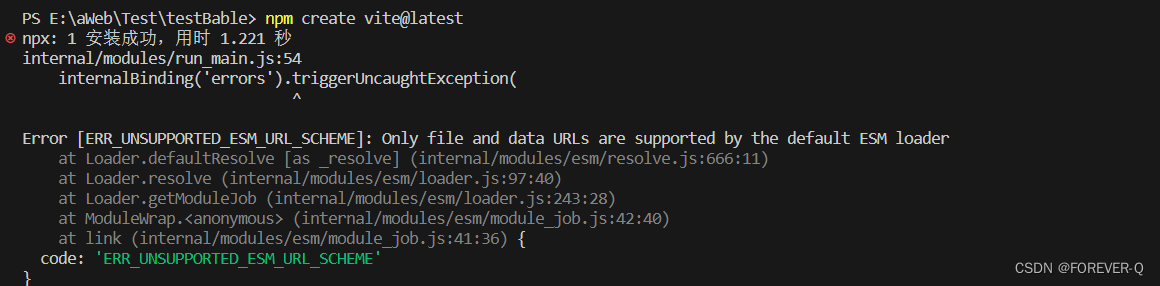
Only file and data URLs are supported by the default ESM loader
1.版本问题 说明:将node版本提高就可以了。 2.nvm 说明:如果不想重复安装node版本,那么可以参考本人的nvm文档. nvm版本控制工具_FOREVER-Q的博客-CSDN博客...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...