深入理解JS作用域链与执行上下文
变量提升:
变量提升( hoisting )。
我可恨的 var 关键字:
你读完下面内容就会明白标题的含义,先来一段超级简单的代码:
<script type="text/javascript">var str = 'Hello JavaScript hoisting';console.log(str); // Hello JavaScript hoisting</script>
这段代码,很意外地简单,我们的到了想要的结果,在控制台打印出了:Hello JavaScript hoisting 。
现在,我将这一段代码,改一改,将 调用 放在前面, 声明 放在后面。
很多语言比如说 C 或者 C++ 都是不允许的,但是 javaScript 允许。
你们试着猜猜得到的结果:
<script type="text/javascript">console.log(str); // undefinedvar str = 'Hello JavaScript hoisting'; console.log(str); // Hello JavaScript hoisting</script>
你会觉得很奇怪,在我们调用之前,为什么我们的 str = undefined ,而不是报错:未定义???
我将 var str = 'Hello JavaScript hoisting' 删除后,试试思考这段代码的结果:
<script type="text/javascript">console.log(str); // Uncaught ReferenceError: str is not defined</script>
现在得到了,我们想要的,报错:未定义。
事实上,在我们浏览器会先解析一遍我们的脚本,完成一个初始化的步骤,它遇到 var 变量时就会先初始化变量为 undefined 。
这就是变量提升(hoisting ),它是指,浏览器在遇到 JS 执行环境的 初始化,引起的变量提前定义。
在上面的代码里,我们没有涉及到函数,因为,我想让代码更加精简,更加浅显,显然我们应该测试一下函数。
<script type="text/javascript">console.log(add); // ƒ add(x, y) { return x + y; }function add(x, y) { return x + y; }</script>
在这里,我们并没有调用函数,但是这个函数,已经被初始化好了,其实,初始化的内容,比我们看到的要多。
如何避免变量提升:
使用 let 和 const 关键字,尽量使用 const 关键字,尽量避免使用 var 关键字;
<script type="text/javascript">// console.log(testvalue1); // 报错:testvalue1 is not defined// let testvalue1 = 'test';/*---------我是你的分割线-------*/console.log(testvalue2); // 报错:testvalue1 is not definedconst testvalue2 = 'test';</script>
但,如果为了兼容也就没办法喽,哈哈哈,致命一击!!!
执行上下文:
执行上下文,又称为执行环境(execution context),听起来很厉害对不对,其实没那么难。

作用域链:
其实,我们知道,JS 用的是 词法作用域 的。
关于 其他作用域 不了解的童鞋,请移步到我的《谈谈 JavaScript 的作用域》,或者百度一下。参考 前端进阶面试题详细解答
每一个 javaScript 函数都表示为一个对象,更确切地说,是 Function 对象的一个实例。
Function 对象同其他对象一样,拥有可编程访问的属性。和一系列不能通过代码访问的 属性,而这些属性是提供给 JavaScript 引擎存取的内部属性。其中一个属性是 [[Scope]] ,由 ECMA-262标准第三版定义。
内部属性 [[Scope]] 包含了一个函数被创建的作用域中对象的集合。
这个集合被称为函数的 作用域链,它能决定哪些数据能被访问到。
来源于:《 高性能JavaScript 》;
我好奇的是,怎样才能看到这个,不能通过代码访问的属性???经过老夫的研究得出,能看到这个东西的方法;
打开谷歌浏览器的 console ,并输入一下代码:
function add(x, y) {return x + y;
}console.log( add.prototype ); // 从原型链上的构造函数可以看到,add 函数的隐藏属性。
可能还有其他办法,但,我只摸索到了这一种。
你需要这样:

然后这样:

好了,你已经看到了,[[Scope]] 属性下是一个数组,里面保存了,作用域链,此时只有一个 global。
思考以下代码,并回顾 词法作用域,结合 [[Scope]] 属性思考,你就能理解 词法作用域 的原理,
var testValue = 'outer';function foo() {console.log(testValue); // "outer"console.log(foo.prototype) // 编号1
}function bar() {var testValue = 'inner';console.log(bar.prototype) // 编号2foo();
}bar();
以下是,执行结果:
编号 1 的 [[Scope]] 属性:Scopes[1] :

编号 2 的 [[Scope]] 属性:Scopes[1]

因为,初始化时,[[Scope]] 已经被确定了,两个函数无论是谁,如果自身的作用域没找到的话,就会在全局作用域里寻找变量。
再思考另外一段代码:
var testValue = 'outer';function bar() {var testValue = 'inner';foo();console.log(bar.prototype) // 编号 1function foo() {console.log(testValue); // "inner"console.log(foo.prototype); // 编号 2 }
}bar();
编号 1 的 [[Scope]] 属性:Scopes[1] :

编号 2 的 [[Scope]] 属性:Scopes[2] :

这就解释了,为什么结果是,testValue = "inner" 。
当 需要调用 testValue 变量时;
先找本身作用域,没有,JS 引擎会顺着 作用域链 向下寻找 [0] => [1] => [2] => […]。
在这里,找到 bar 函数作用域,另外有趣的是,Closure 就是闭包的意思 。

证明,全局作用域链是在 全局执行上下文初始化时 就已经确定的:
我们来做一个有趣的实验,跟刚才,按照我描述的方法,你可以找到 [[Scope]] 属性。
那这个属性是在什么时候被确定的呢???
很显然,我们需要从,函数声明前,函数执行时,和函数执行完毕以后三个方面进行测试:
console.log(add.prototype); // 编号1 声明前function add(x, y) {console.log(add.prototype); // 编号2 运行时return x + y;
}add(1, 2);
console.log(add.prototype); // 编号3 执行后
编号1 声明前:

编号2 运行时:

编号3 执行后:

你可按照我的方法,做很多次实验,试着嵌套几个函数,在调用它们之前观察作用域链。
作用域链,是在 JS 引擎 完成 初始化执行上下文环境,已经确定了,这跟我们 变量提升 小节讲述得一样。
它保证着 JS 内部能正常查询 我们需要的变量!。
我的一点疑惑
注意:在这里,我无法证明一个问题。
- 全局执行上下文初始化完毕之后,它是把所有的函数作用域链确定。
- 还是,初始化一个执行上下文,将本作用域的函数作用域链确定。
这是我的疑惑,我无法证明这个问题,但是,我更倾向于 2 的观点,如果知道如何证明请联系我。至少,《高性能JavaScript》中是这样描述的。
知道作用域链有什么好处?
试想,我们知道作用域链,有什么用呢???
我们知道,如果作用域链越深, [0] => [1] => [2] => […] => [n],我们调用的是 全局变量,它永远在最后一个(这里是第 n 个),这样的查找到我们需要的变量会引发多大的性能问题?JS 引擎查找变量时会耗费多少时间?
所以,这个故事告诉我们,尽量将 全局变量局部化 ,避免,作用域链的层层嵌套,所带来的性能问题。
理解 执行上下文:
将这段代码,放置于全局作用域之下。这一段代码,改编自《高性能JavaScript》。
function add(x, y) {return x + y;
}var result = add(1, 2);
这段代码也很简洁,但在 JavaScript 引擎内部发生的事情可并不简单。
正如,上一节,变量提升 所论述,JS 引擎会初始化我们声明 函数 和 变量 。
那么在 add(1, 2) 执行前,我们的 add 函数 [[Scope]] 内是怎样的呢???
这里有三个时期:初始化 执行上下文、运行 执行上下文、结束 执行上下文。
很显然,执行到 var result = add(1, 2) 句时,是程序正在准备:初始化执行上下文 。

如上图所示,在函数未调用之前,已经有 add 函数的[[Scope]]属性所保存的 作用域链 里面已经有这些东西了。
当执行此函数时,会建立一个称为 执行上下文 (execution context) 的内部对象。
一个 执行上下文 定义了一个函数执行时的环境,每次调用函数,就会创建一个 执行上下文 ;
一旦初始化 执行上下文 成功,就会创建一个 活动对象 ,里面会产生 this arguments 以及我们声明的变量,这个例子里面是 x、y。
运行执行上下文 阶段:

结束 执行上下文 阶段:

好了,但是,这里没有涉及到调用其他函数。
其实,还有,我们的 JavaScript 引擎是如何管理,多个函数之间的 执行上下文 ???
相关文章:

深入理解JS作用域链与执行上下文
变量提升: 变量提升( hoisting )。 我可恨的 var 关键字: 你读完下面内容就会明白标题的含义,先来一段超级简单的代码: <script type"text/javascript">var str Hello JavaScript hoi…...
UnityEditor编辑器扩展代码实现Project搜索的实现功能和切换Component等
反射实现切换Gameobjecect-Comp之前介绍过Kinematic Character Controller这个插件这个插件很容易和另外一个插件混淆,两个作者头像比较相像,而且这个插件的作者不太喜欢露脸(他现在做Dot-CharacterControl去了),几乎网…...

SKAdNetwork:从0到1
一、什么是SKAdNetwork https://developer.apple.com/documentation/storekit/skadnetwork iOS14.5开始,获取IDFA需要用户确认授权才可,此时SKAdNetwork 正式回归。 SKAdNetwork 是苹果在2018年推出的一个更加保护用户隐私的归因框架,并与…...

Spring+MVC+MYbatis注解开发
Spring常见注解 注解一:Configuration 用在类上面,加上这个注解的类可以成为一个spring的xml配置文件,使用的是java代码的配置 注解二:ComponentScan 用在类上,加上注解可以指定扫描路径 注解三:创建对…...

Redis主从复制过程
将目前服务器加入到端口号为6379的从服务器 一主二仆 当期中一台从服务器宕机之后 从服务器重启之后会变成单独的主服务器,与之前的主从复制没有关系,重新使用slaceof命令才能恢复到之前一样 主服务器宕机后,从服务器不会成为主服务器&…...
Spring boot开启定时任务的三种方式(内含源代码+sql文件)
Spring boot开启定时任务的三种方式(内含源代码sql文件) 源代码sql文件下载链接地址:https://download.csdn.net/download/weixin_46411355/87486580 目录Spring boot开启定时任务的三种方式(内含源代码sql文件)源代码…...

Tekton实战案例--S2I
案例环境说明 示例项目: 代码仓库:https://gitee.com/mageedu/spring-boot-helloWorld.git 构建工具maven pipeline各Task git-clone:克隆项目的源代码 build-to-package: 代码测试,构建和打包 generate-build-id:生…...

四、使用类实现功能
使用类实现功能 ts中类的继承 ES6中class类中,属性分为:实例上的属性,原型上的方法;也可以叫做:class的属性,class的方法。 类的继承叫法:父类>子类,基类>派生类;…...

Java多线程不安全的例子
目录 1. 可见性不安全例子 2. 原子性不安全例子 3. 有序性不安全例子 1. 可见性不安全例子 可见性:一个线程对共享变量的修改,另外一个线程不能够立刻看到。 如果多线程对共享数据进行访问而不采取同步操作的话,那么操作的结果是不一致…...

vivo X Flip会是高端手机市场的又一折叠屏爆款吗?
据多个平台消息,vivo即将推出小折叠屏手机X Flip。据了解,vivo X Flip将采用轻盈便携的竖向折叠布局,以及非常受女性消费者喜爱的结构设计。那么,vivo X Flip会是vivo折叠屏的又一个爆款吗? 一、vivo X Flip小折叠屏手…...
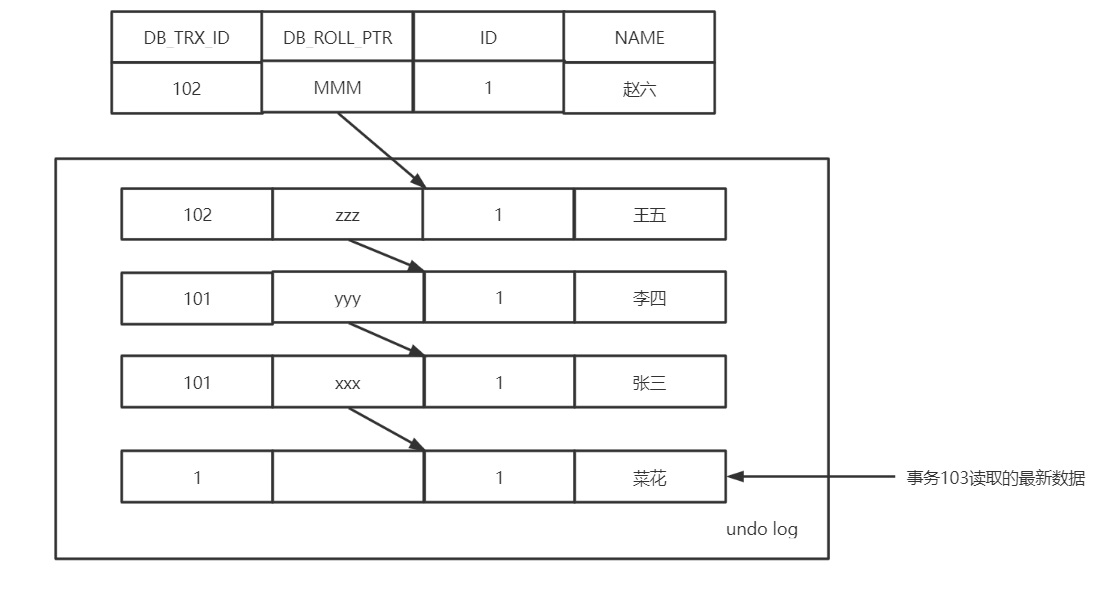
MySQL中MVCC如何解决不可重复读以及幻读?
了解MVCC之前,我们首先需要了解以下两个概念:一致性非锁定读和锁定读,了解这两个概念之后我们在逐步分析MVCC。 一致性非锁定读和锁定读 一致性非锁定读(快照读) 对于 一致性非锁定读的实现,通常做法是加一个版本号或者时间戳字…...

设计模式第八讲:观察者模式和中介者模式详解
一. 观察者模式 1. 背景 在现实世界中,许多对象并不是独立存在的,其中一个对象的行为发生改变可能会导致一个或者多个其他对象的行为也发生改变。例如,某种商品的物价上涨时会导致部分商家高兴,而消费者伤心;还有&…...

关于 mac 本地配置域名能 ping 通,但是浏览器不能访问的问题(而其他电脑操作可访问)
关于 mac 本地配置域名能 ping 通,但是浏览器不能访问的问题(而其他电脑操作可访问)1. 配置域名的方式1.1 sudo vim /etc/hosts1.2 浏览器插件 LiveHosts2. 问题描述3. 解决问题方法3.1 尝试方法1—确保代理都关闭3.2 尝试方法2—确保域名能p…...

【代码随想录二刷】Day23-二叉树-C++
代码随想录二刷Day23 今日任务 669.修剪二叉搜索树 108.将有序数组转换为二叉搜索树 538.把二叉搜索树转换为累加树 语言:C 669. 修剪二叉搜索树 链接:https://leetcode.cn/problems/trim-a-binary-search-tree/ 递归 class Solution { public:Tree…...
Linux GPIO 开发指南
文章目录Linux GPIO 开发指南1 概述1.1 编写目的1.2 适用范围1.3 相关人员2 模块介绍2.1 模块功能介绍2.2 相关术语介绍2.3 总体框架2.4 state/pinmux/pinconfig2.5 源码结构介绍3 模块配置3.1 kernel menuconfig 配置3.2 device tree 源码结构和路径3.2.1 device tree 对 gpio…...
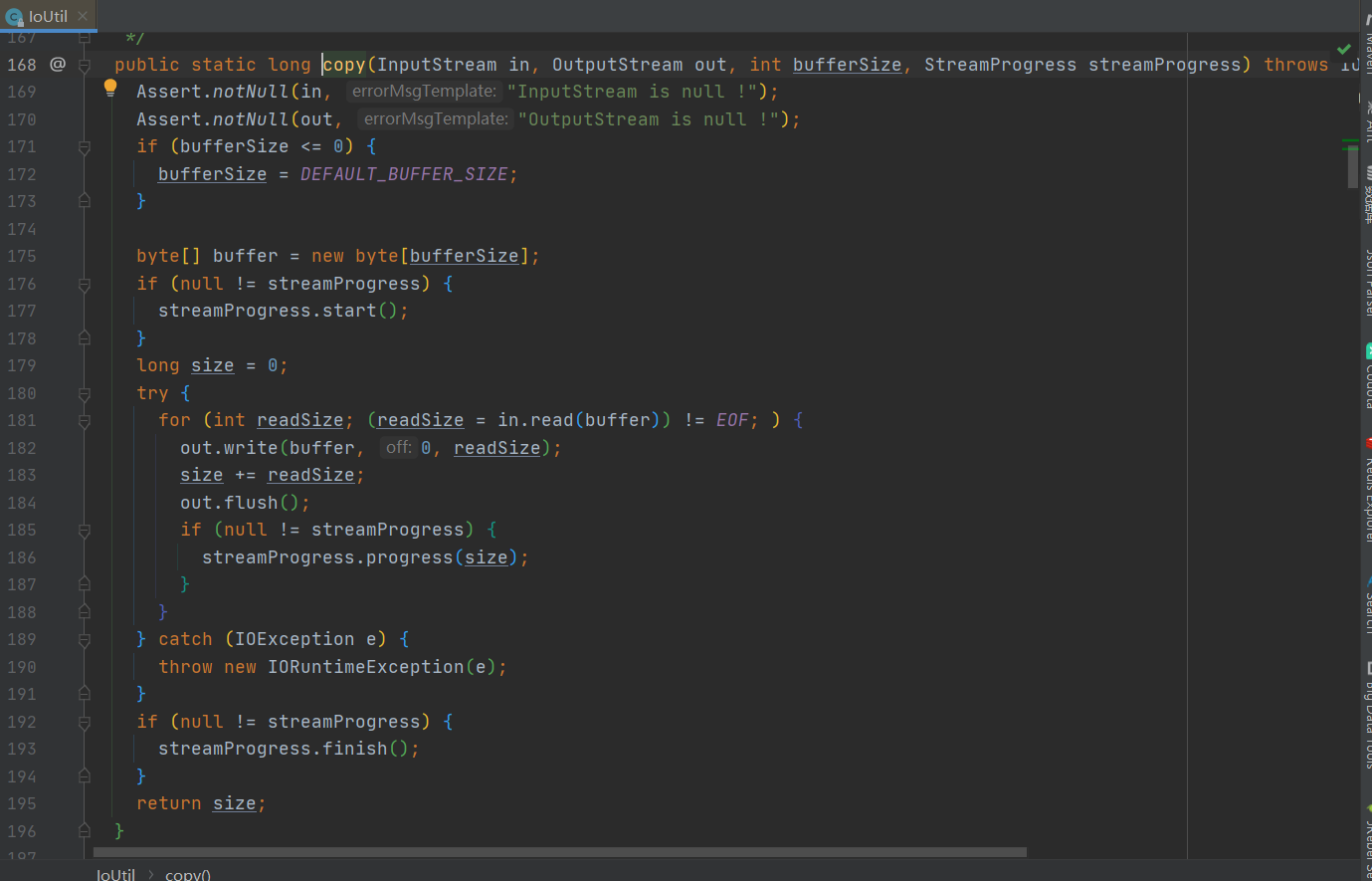
记一次后端生成Zip文件通过浏览器下载后文件损坏,无法打开,不可预知的末端错误,下载后文件比源文件增大
记一次后端生成Zip文件问题前言问题出现排查一、流没有关好二、写入了空白字节三、没有flush定位环节一、生成二、通过SwaggerUI、PostMan进行下载三、结论解决方法前言 在项目上线前夕,临时添加了个数据导出的接口,需求是导出压缩包,选择了项…...
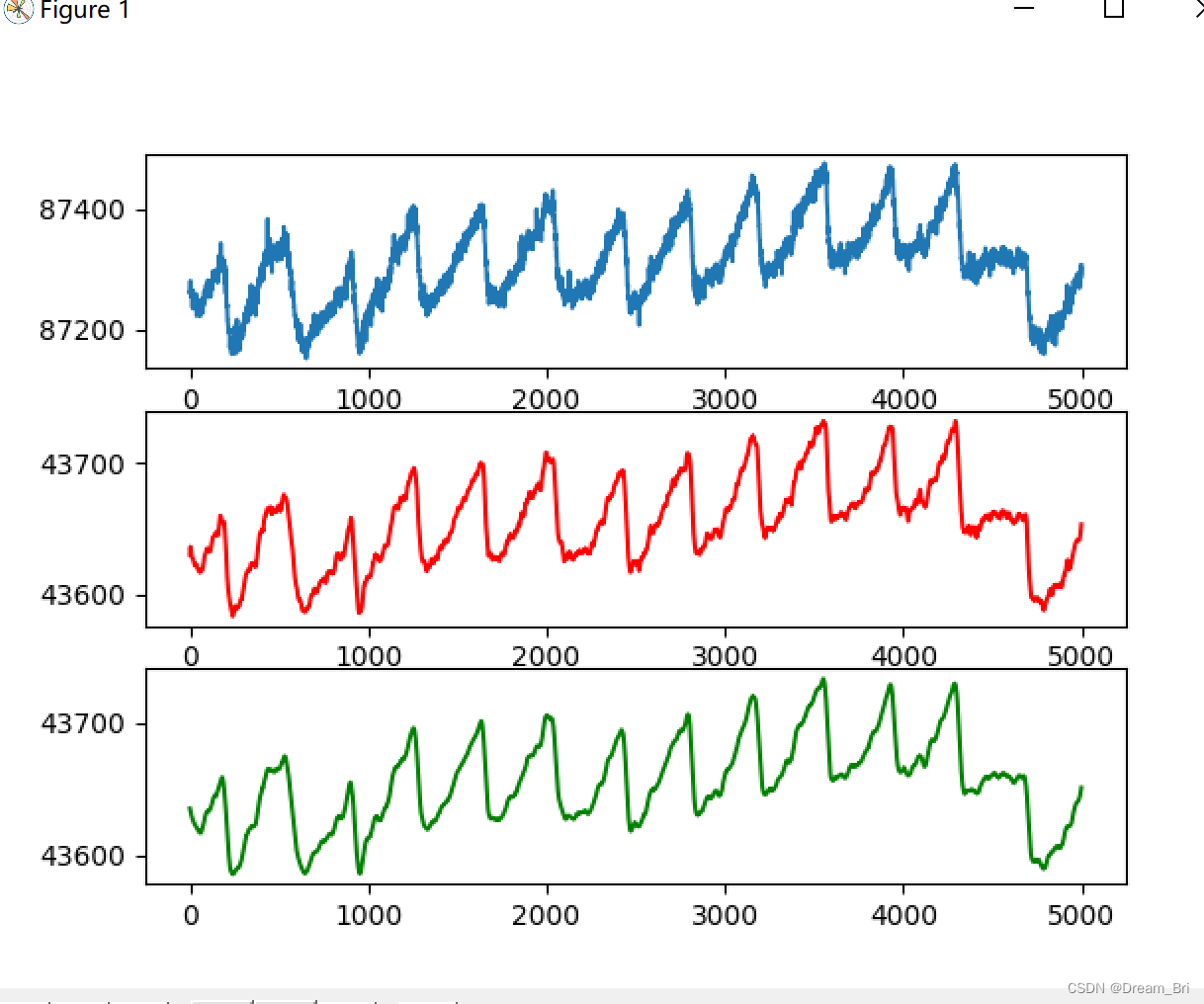
python中savgol_filter的详细解释
目录savgol_filter简介savgol_filter原理参数window_length对平滑的效果参数polyorder的平滑效果savgol_filter简介 Savitzky-Golay滤波器最初由Savitzky和Golay于1964年提出,是光谱预处理中常用滤波方法,它的核心思想是对一定长度窗口内的数据点进行k阶…...
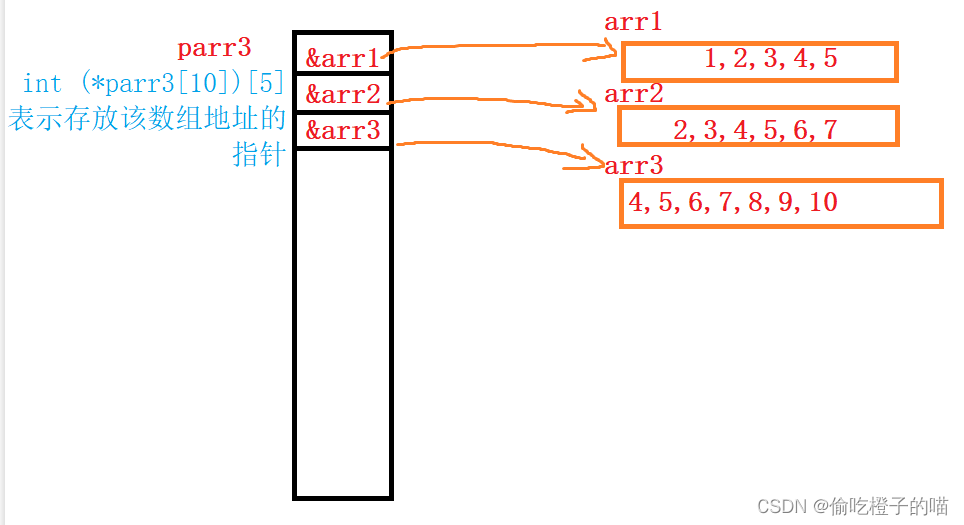
C语言--指针进阶1
目录回顾字符指针指针数组数组指针&数组名和数组名的区别数组指针的使用指针作为形参练习数组参数、指针参数一维数组传参二维数组传参一级指针传参二级指针传参回顾 指针的内容,我们在初级阶段已经有所涉及了,我们先来复习一下 指针就是个变量&am…...
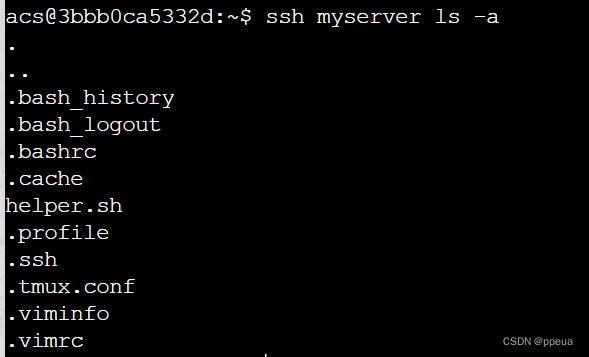
ssh的使用
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...

Apache Hadoop生态-目录汇总-持续更新
目录 1:系统服务分布图 3台分布式架构 1台单机架构 服务版本介绍 2:服务目录 存储相关 数据采集 任务调度 即席查询 数据可视化 集群监控 元数据管理 用户认证 权限管理 第三方windows客户端 1:系统服务分布图 3台分布式架构…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...
