【C++杂货铺】一颗具有搜索功能的二叉树

文章目录
- 一、二叉搜索树概念
- 二、二叉搜索树的操作
- 2.1 二叉搜索树的查找
- 2.2 二叉搜索树的插入
- 2.3 二叉搜索树的删除
- 三、二叉搜索树的实现
- 3.1 BinarySearchTreeNode(结点类)
- 3.2 BinarySearchTree(二叉搜索树类)
- 3.2.1 框架
- 3.2.2 insert(插入)
- 3.2.3 InOrder(中序遍历)
- 3.2.4 find(查找)
- 3.2.5 erase(删除)
- 3.2.6 ~BinarySearchTree(析构)
- 3.2.7 BinarySearchTree(const Self& tree)(拷贝构造)
- 3.2.8 operator=(赋值运算符重载)
- 四、二叉搜索树的应用
- 4.1 K模型
- 4.2 KV模型
- 4.2.1 KV 模型手撕
- 五、二叉搜索树的性能分析
- 六、结语
一、二叉搜索树概念
二叉搜索树又称二插排序树,它要么是一个空树,要么就是具有以下性质的二叉树:
-
若它的左子树不为空,则左子树上所有节点的值都小于(大于)根节点的值。
-
若它的右子树不为空,则右子树上所有节点的值都大于(小于)根节点的值。
-
它的左右子树也分别为二叉搜索树。

二、二叉搜索树的操作
2.1 二叉搜索树的查找
-
从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
-
最多查找高度次,走到空还没找到,说明这个值不存在。
小Tips:这里最多查找高度次的时间复杂度并不是 O ( l o g N ) O(logN) O(logN),这是建立在比较理想的情况下,即这颗二叉树是一颗满二叉树或者完全二叉树。在极端情况下,这棵二叉树只有一条路径,此时最多查找高度次的时间复杂度就是 O ( N ) O(N) O(N)。
2.2 二叉搜索树的插入
插入的具体过程如下:
-
树为空:则直接新增节点,赋值给 root 指针。
-
树不为空:先按二叉搜索树的性质寻找插入位置,插入新节点。

2.3 二叉搜索树的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回,否则要删除的结点可能分下面四种情况:
-
要删除的结点没有孩子结点。
-
要删除的结点只有左孩子结点。
-
要删除的结点只有右孩子结点。
-
要删除的结点有左、右孩子节点。
虽然看起来删除一个结点有 4 中情况,但实际上情况1可以和情况2或者情况3合并起来,因此真正的删除过程如下:
-
情况一(要删除的结点只有左孩子):删除该节点且使被删除节点的双亲结点指向被删除结点的左孩子结点----直接删除。
-
情况二(要删除的结点只有右孩子):删除该结点且使被删除结点的双亲结点指向被删除结点的右孩子结点-----直接删除。
-
情况三(要删除的结点有左、右孩子):在它的左子树中寻找出关键码最大的结点,用它的值填补到被删除结点中,再来处理该结点的删除问题----替换法删除。

三、二叉搜索树的实现
二插搜索树只是一种结构,它本质上是由一个个结点链接而成,因此我们首先需要定义一个结点类,这个结点用来存储数据。有了结点类之后就需要定义一个二叉搜索树的类,这个类主要是用来维护结构的,实现增删查改等功能,因为它是维护结构的,因此这个类里面的成员变量只需要一个根节点即可,有了这个根节点就能对整个数的结构进行维护管理。
3.1 BinarySearchTreeNode(结点类)
template <class K>
struct BinarySearchTreeNode
{typedef BinarySearchTreeNode<K> TNode;BinarySearchTreeNode(const K& val = K()):_val(val),_left(nullptr),_right(nullptr){}K _val;TNode* _left;TNode* _right;
};
3.2 BinarySearchTree(二叉搜索树类)
3.2.1 框架
template <class K>
class BinarySearchTree
{typedef BinarySearchTreeNode<K> BSTNode;typedef BinarySearchTree<K> Self;
public:BinarySearckTree():_root(nullptr){}
private:BSTNode* _root;
};
3.2.2 insert(插入)
非递归版:
bool insert(const K& val)
{if (_root == nullptr){_root = new BSTNode(val);return true;}BSTNode* newnode = new BSTNode(val);BSTNode* cur = _root;BSTNode* parent = nullptr;while (cur){if (val < cur->_val){parent = cur;cur = cur->_left;}else if (val > cur->_val){parent = cur;cur = cur->_right;}else{return false;//相等就说明树中已经有了,就应该插入失败}}//if (parent->_left == cur)//左右都是空,每次就走上面这个了if(val < parent->_val){parent->_left = newnode;}else{parent->_right = newnode;}return true;
}
小Tips:需要单独考虑根节点为空的情况。用 cur 找到该结点应该要插入的位置,用 parent 指向该位置的双亲结点,以实现链接关系。最后还需要判断插入到双亲结点的左侧还是右侧。我们实现的这个二叉搜索树要求存储相同值的结点在一个二叉搜索树中只能出现一次,因此当插入一个值 val 的时候,如果检测到树中已经有一个结点存的是 val,那么就应该返回 false,表明插入失败。
递归版:
//插入(递归---版本一)
private:bool _InsertR(BSTNode*& root, BSTNode* parent, const K& key){if (root == nullptr)//为空说明就是在该位置插入{BSTNode* newnode = new BSTNode(key);if (parent != nullptr){if (key < parent->_val){parent->_left = newnode;}else{parent->_right = newnode;}}else{root = newnode;}return true;}//root不为空说明还没有找到待插入的位置,还得继续找if (key < root->_val){return _InsertR(root->_left, root, key);}else if (key > root->_val){return _InsertR(root->_right, root, key);}else{return false;}}
public://插入(递归)bool InsertR(const K& key){return _InsertR(_root, _root, key);}
//插入(递归---版本二)
private:bool _InsertR(BSTNode*& root, const K& key){if (root == nullptr)//为空说明就是在该位置插入{root = new BSTNode(key);return true;}//root不为空说明还没有找到待插入的位置,还得继续找if (key < root->_val){return _InsertR(root->_left, key);}else if (key > root->_val){return _InsertR(root->_right, key);}else{return false;}}
public://插入(递归)bool InsertR(const K& key){return _InsertR(_root, key);}
小Tips:在空树的时候执行插入,是需要改变根节点 _root 的,即需要对指针进行修改,因此这里需要使用引用或者二级指针。
3.2.3 InOrder(中序遍历)
private:void _InOrder(BSTNode* root) const{if (root == nullptr){return;}_InOrder(root->_left);cout << root->_val << " ";_InOrder(root->_right);}
public:void InOrder(){_InOrder(_root);cout << endl;}
小Tips:这里的中序遍历用的是递归的方式来实现的,但是递归函数一定是需要一个参数的,要中序遍历整个二叉树,用户一定是要把根节点 _root 传给这个函数,但是根节点 _root 是私有的成员变量,用户是访问不到的,因此我们不能直接提供中序遍历函数给用户。正确的做法是,虽然用户访问不到根结点,但是类里面可以访问呀,所以我们可以在类里面实现一个中序遍历的子函数 _InOrder,在这个子函数中实现中序遍历的逻辑,然后我们再去给用户提供一个中序遍历的函数接口 InOrder,由它去调用 _InOrder。这样以来用户就可以正常去使用中序遍历啦。
3.2.4 find(查找)
非递归版:
bool find(const K& key)
{BSTNode* cur = _root;while (cur){if (key < cur->_val){cur = cur->_left;}else if (key > cur->_val){cur = cur->_right;}else{return true;}}return false;
}
递归版:
private:bool _FindR(BSTNode* root, const K& key){if (root == nullptr){return false;}if (key < root->_val){return _FindR(root->_left, key);}else if (key > root->_val){return _FindR(root->_right, key);}else{return true;}}
public:bool FindR(const K& key){return _FindR(_root, key);}
3.2.5 erase(删除)
非递归版:
bool erase(const K& key)
{BSTNode* cur = _root;BSTNode* parent = nullptr;//先找需要删除的结点while (cur){if (key < cur->_val){parent = cur;cur = cur->_left;}else if (key > cur->_val){parent = cur;cur = cur->_right;}else{//到这里说明cur就是待删除的节点if (cur->_left == nullptr)//如果cur只有一个孩子(只有右孩子),直接托孤{if (parent == nullptr)//说明删除的是根结点{_root = _root->_right;}else if (cur == parent->_left)//判断cur是左孩子还是右孩子{parent->_left = cur->_right;}else if(cur == parent->_right){parent->_right = cur->_right;}}else if(cur->_right == nullptr)//如果cur只有一个孩子(只有左孩子){if (parent == nullptr)//说明删除的是根结点{_root = _root->_left;}else if (cur == parent->_left)//判断cur是左孩子还是右孩子{parent->_left = cur->_left;}else if (cur == parent->_right){parent->_right = cur->_left;}}else//到这里说明cur有两个孩子{BSTNode* parent = cur;BSTNode* leftmax = cur->_left;//找到左孩子中最大的那个while (leftmax->_right){parent = leftmax;leftmax = leftmax->_right;}swap(cur->_val, leftmax->_val);cur = leftmax;//有一种极端情况就是左边只有一条路径if (leftmax == parent->_left){parent->_left = leftmax->_left;}else{parent->_right = leftmax->_left;}}delete cur;return true;}}return false;
}
小Tips:在上面的代码中我们始终让 cur 指向待删除节点,parent 指向待删除结点的双亲,也就是 cur 的双亲。删除大体上就分为2. 3小节中提到的三种情况。但是里面任然有一些细节需要我们注意,比如删除根结点的情况,即 parent == nullptr 的时候。在情况一和情况二中,我们还需要判断待删除结点 cur 是其双亲结点 parent 的左孩子还是右孩子,以保证让 cur 的孩子和 parent 建立正确的链接关系。情况三,待删除的结点有两个孩子,我们这里的做法是,找出 cur 左子树中最大的那个节点 leftmax,让它来替换 cur,帮助 cur 带“孩子”。找到左子树中值最大的结点很容易,从 cur 的左孩子开始,一路往右即可。找到后交换 cur 和 leftmax 中存储的值。交换后 leftmax 就变成了要删除的结点,所以所以此时需要让 cur 重新指向 leftmax 这个结点。由于要删除 leftmax 结点,为了方便后面修改链接关系,这里我们还需要找到 leftmax 的双亲结点,因此在这个局部域中我们重新定义了一个 parent,它和外面那个 parent 并不冲突,优先使用局部的,但是注意里面这个 parent 表示的意义和外面 parent 的意义是有所不同的,前者表示 cur 左树中最大节点的双亲结点,后者表示 cur 的双亲结点。最后我们需要通过修改链接关系来实现 cur 结点的删除,这里的链接关系有以下两种情形:
情形一:

小Tips:Step2 中的交换是交换节点中的值,并不是交换两个结点。最终 leftmax 和 cur 指向同一个结点。
情形二:

小Tips:情形二与情形一最大的不同点体现在两个地方,第一情形二中的 parent 就是 cur,只说明我们在定义 parent 赋初值的时候不能让 parent = nullptr,应该让 parent = cur,否则后面修改链接关系会出现访问空指针的问题。第二点不同在于修改链接关系,情形二是让 parent 的左孩子指向 leftmax 的左孩子;情形一是让 parent 的右孩子指向 leftmax 的左孩子。因此在修改链接关系的时候要进行判断,看是哪种情形。在第二点不同里面又有一个相同点,即无论是 parent 的左孩子,还是 parent 的右孩子,最终都指向了 leftmax 的左孩子,这是为什么呢?原因其实很简单,leftmax 的右孩子一定为空,而左孩子则不一定为空。为什么可以肯定右孩子一等为空,因为 leftmax 是左子树中最大的那个结点,如果它的右孩子不为空,说明当前这个 leftmax 一定不是最大的那个结点。因此在修改链接关系的时候,要让 parent 与 leftmax 的左孩子建立连接。最后需要注意,交换完之后,只能通过修改链接关系去删除 cur 结点,不能通过递归调用去删除,因为这个函数每次都是从根节点开始查找的,交换后这棵树暂时不满足二叉搜索树的结构,以情形一为例,它就找不到存储8的结点。
递归版:
private:
//删除递归版bool _eraseR(BSTNode*& root, const K& key){if (root == nullptr){return false;}if (key < root->_val){return _eraseR(root->_left, key);}else if (key > root->_val){return _eraseR(root->_right, key);}else{//相等了,需要进行删除了BSTNode* del = root;if (root->_left == nullptr)//左为空{root = root->_right;}else if (root->_right == nullptr)//右为空{root = root->_left;}else//左右都不为空{BSTNode* parent = root;BSTNode* leftmax = root->_left;//找到左孩子中最大的那个while (leftmax->_right){parent = leftmax;leftmax = leftmax->_right;}swap(root->_val, leftmax->_val);return _eraseR(root->_left, key);}delete del;del = nullptr;return true;}}
public://删除递归版bool eraseR(const K& key){return _eraseR(_root, key);}
小Tips:在交换后,虽然整棵树可能不满足二叉搜索树的结构,但是 root 结点的左子树一定是满足二叉搜索树的,因为我们交换的是 root 结点的 _val 和左子树中最大的那个 _val,而 root 结点的 _val 一定是比左子树中最大的那个 _val 还要大的,所以交换完之后 root 的左子树任然满足二叉搜索树的结构,此时我们就可以通过递归调用去 root 的左子树中找要删除的结点,并且交换后待删除的结点一定变成了情况一或者情况二中的一种。递归版中对情况一和情况二的处理变简单了许多,因为 root 是一个引用,如果发现 root 的一个孩子为空,直接把 root 的另一个孩子赋值给它即可,在赋值之前记得保存一下 root 的值,这个值指向的结点就是要删除的结点,把这个值保存下来后面才能去 delete,否则赋值后就没有指针指向该结点,那就没办法释放这个结点的空间资源,就会造成内存泄漏。非递归中即使用了引用也不能这样搞,因为非递归中,一个引用始终是在一个函数栈帧里面,而引用是不能改变指向的。但是递归就不一样了,每一次递归调用都会开辟新的函数栈帧,每一个函数栈帧中 root 都是不同结点的别名。
3.2.6 ~BinarySearchTree(析构)
private://析构子函数void Destruction(BSTNode*& root){if (root == nullptr){return;}//先去释放左孩子和右孩子的空间资源Destruction(root->_left);Destruction(root->_right);//再去释放root自己的空间资源delete root;root = nullptr;//形参root如果不加引用,这里置空是没有任何意义的,因为不加引用这里仅仅是一份拷贝return;}
public://析构函数~BinarySearckTree(){Destruction(_root);}
3.2.7 BinarySearchTree(const Self& tree)(拷贝构造)
注意拷贝构造不能直接去调用 insert,因为数据插入的顺序不同,这棵树最终的结构也是不同的,虽然最终也符合二叉树的结构,但是还是和被拷贝的树有所不同。正确做法是,走一个前序遍历,遍历到 tree 的一个结点时,去 new 一个结点,存储同样的值。
写法一:
//拷贝构造函数的子函数
private:void Construct(BSTNode*& root, BSTNode* copy){if (copy == nullptr){root = nullptr;return;}root = new BSTNode(copy->_val);//通过引用直接来实现链接关系Construct(root->_left, copy->_left);Construct(root->_right, copy->_right);}
public://拷贝构造BinarySearchTree(const Self& tree):_root(nullptr){Construct(_root, tree._root);}
写法二:
private:
//拷贝构造子函数(写法二)BSTNode* Construct(BSTNode* root){if (root == nullptr){return nullptr;}BSTNode* newnode = new BSTNode(root->_val);newnode->_left = Construct(root->_left);//通过返回值来实现链接关系newnode->_right = Construct(root->_right);return newnode;}
public://拷贝构造(写法二)BinarySearchTree(const Self& tree){_root = Construct(tree._root);}
小Tips:上面两种写法的不同点在于,方法一是通过引用去实现链接关系,方法二则是通过返回值的方式来实现链接关系。
3.2.8 operator=(赋值运算符重载)
public:
//赋值运算符重载(现代写法)Self& operator=(Self tree){swap(_root, tree._root);//交换两颗搜索二叉树就是交换它们里面维护的根节点return *this;}
四、二叉搜索树的应用
4.1 K模型
K模型即只有一个 Key 作为关键码,结构中只需要存储 Key 即可,关键码即为需要搜索到的值。比如:给一个单词 word,判断该单词是否拼写正确,具体方式如下:
-
以词库中所有单词集合中的每个单词作为 Key,构建一颗二叉搜索树。
-
在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
我们上面手搓的这可二叉搜索树就是 Key 模型,因为这颗树的结点里面只能存储一个值,这个值就是 Key。
4.2 KV模型
KV 模型即每一个关键码 Key,都有与之对应的的值 Value,即 <Key,Value> 的键值对。这种方式在现实生活中十分常见:
-
比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文 <word,Chinese> 就构成一种键值对。
-
再比如统计单词次数,统计成功后,给定单词就可以快速找到其出现的次数,单词与其出现次数就是 <word,count> 就构成一种键值对。
4.2.1 KV 模型手撕
#pragma oncenamespace K_V
{template <class K, class V>struct BinarySearchTreeNode{typedef BinarySearchTreeNode<K, V> TNode;BinarySearchTreeNode(const K& key = K(), const V& val = V()):_key(key), _val(val), _left(nullptr), _right(nullptr){}K _key;V _val;TNode* _left;TNode* _right;};template <class K, class V>class BinarySearchTree{typedef BinarySearchTreeNode<K, V> BSTNode;typedef BinarySearchTree<K, V> Self;private:void _InOrder(BSTNode* root) const{if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << "--" << root->_val << endl;_InOrder(root->_right);}BSTNode* _FindR(BSTNode* root, const K& key)//KV模型中的Key不能被修改,但是Val可以被修改{if (root == nullptr){return nullptr;}if (key < root->_key){return _FindR(root->_left, key);}else if (key > root->_key){return _FindR(root->_right, key);}else{return root;}}//插入(递归---版本一)//bool _InsertR(BSTNode*& root, BSTNode* parent, const K& key)//{// if (root == nullptr)//为空说明就是在该位置插入// {// BSTNode* newnode = new BSTNode(key);// if (parent != nullptr)// {// if (key < parent->_key)// {// parent->_left = newnode;// }// else// {// parent->_right = newnode;// }// }// else// {// root = newnode;// }// return true;// }// //root不为空说明还没有找到待插入的位置,还得继续找// if (key < root->_key)// {// return _InsertR(root->_left, root, key);// }// else if (key > root->_key)// {// return _InsertR(root->_right, root, key);// }// else// {// return false;// }//}//插入(递归---版本二)bool _InsertR(BSTNode*& root, const K& key, const V& val){if (root == nullptr)//为空说明就是在该位置插入{root = new BSTNode(key, val);return true;}//root不为空说明还没有找到待插入的位置,还得继续找if (key < root->_key){return _InsertR(root->_left, key, val);}else if (key > root->_key){return _InsertR(root->_right, key, val);}else{return false;}}//删除递归版bool _eraseR(BSTNode*& root, const K& key){if (root == nullptr){return false;}if (key < root->_key){return _eraseR(root->_left, key);}else if (key > root->_key){return _eraseR(root->_right, key);}else{//相等了,需要进行删除了BSTNode* del = root;if (root->_left == nullptr)//左为空{root = root->_right;}else if (root->_right == nullptr)//右为空{root = root->_left;}else//左右都不为空{BSTNode* parent = root;BSTNode* leftmax = root->_left;//找到左孩子中最大的那个while (leftmax->_right){parent = leftmax;leftmax = leftmax->_right;}std::swap(root->_key, leftmax->_key);return _eraseR(root->_left, key);}delete del;del = nullptr;return true;}}//析构子函数void Destruction(BSTNode*& root){if (root == nullptr){return;}//先去释放左孩子和右孩子的空间资源Destruction(root->_left);Destruction(root->_right);//再去释放root自己的空间资源delete root;root = nullptr;//形参root如果不加引用,这里置空是没有任何意义的,因为不加引用这里仅仅是一份拷贝return;}//拷贝构造函数的子函数(写法一)void Construct(BSTNode*& root, BSTNode* copy){if (copy == nullptr){root = nullptr;return;}root = new BSTNode(copy->_key);Construct(root->_left, copy->_left);Construct(root->_right, copy->_right);}//拷贝构造子函数(写法二)BSTNode* Construct(BSTNode* root){if (root == nullptr){return nullptr;}BSTNode* newnode = new BSTNode(root->_key);newnode->_left = Construct(root->_left);newnode->_right = Construct(root->_right);return newnode;}public:BinarySearchTree():_root(nullptr){}//拷贝构造(写法一)/*BinarySearchTree(const Self& tree):_root(nullptr){Construct(_root, tree._root);}*///拷贝构造(写法二)BinarySearchTree(const Self& tree){_root = Construct(tree._root);}//赋值运算符重载(现代写法)Self& operator=(Self tree){swap(_root, tree._root);//交换两颗搜索二叉树就是交换它们里面维护的根节点return *this;}//插入(非递归)bool insert(const K& key, const V& val){if (_root == nullptr){_root = new BSTNode(key, val);return true;}BSTNode* newnode = new BSTNode(key, val);BSTNode* cur = _root;BSTNode* parent = nullptr;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{return false;//相等就说明树中已经有了,就应该插入失败}}//if (parent->_left == cur)//左右都是空,每次就走上面这个了if (key < parent->_key){parent->_left = newnode;}else{parent->_right = newnode;}return true;}//插入(递归)bool InsertR(const K& key, const V& val){return _InsertR(_root, key, val);}//中序遍历void InOrder(){_InOrder(_root);cout << endl;}//查找(非递归)BSTNode* find(const K& key){BSTNode* cur = _root;while (cur){if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}else{return cur;}}return nullptr;}//查找(递归)BSTNode* FindR(const K& key){return _FindR(_root, key);}//删除(非递归)bool erase(const K& key){BSTNode* cur = _root;BSTNode* parent = nullptr;//先找需要删除的结点while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{//到这里说明cur就是待删除的节点if (cur->_left == nullptr)//如果cur只有一个孩子(只有右孩子),直接托孤{if (parent == nullptr){_root = _root->_right;}else if (cur == parent->_left)//判断cur是左孩子还是右孩子{parent->_left = cur->_right;}else if (cur == parent->_right){parent->_right = cur->_right;}}else if (cur->_right == nullptr)//如果cur只有一个孩子(只有左孩子){if (parent == nullptr){_root = _root->_left;}else if (cur == parent->_left)//判断cur是左孩子还是右孩子{parent->_left = cur->_left;}else if (cur == parent->_right){parent->_right = cur->_left;}}else//到这里说明cur有两个孩子{BSTNode* parent = cur;BSTNode* leftmax = cur->_left;//找到左孩子中最大的那个while (leftmax->_right){parent = leftmax;leftmax = leftmax->_right;}std::swap(cur->_key, leftmax->_key);cur = leftmax;//有一种极端情况就是左边只有一条路径if (leftmax == parent->_left){parent->_left = leftmax->_left;}else{parent->_right = leftmax->_left;}}delete cur;return true;}}return false;}//删除递归版bool eraseR(const K& key){return _eraseR(_root, key);}//析构函数~BinarySearchTree(){Destruction(_root);}private:BSTNode* _root = nullptr;};
}void TestBSTree4()
{// 统计水果出现的次数string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜","苹果", "香蕉", "苹果", "香蕉" };K_V::BinarySearchTree<string, int> countTree;for (const auto& str : arr){// 先查找水果在不在搜索树中// 1、不在,说明水果第一次出现,则插入<水果, 1>// 2、在,则查找到的节点中水果对应的次数++//BSTreeNode<string, int>* ret = countTree.Find(str);auto ret = countTree.FindR(str);if (ret == NULL){countTree.insert(str, 1);}else{ret->_val++;}}countTree.InOrder();
}

小Tips:虽然变成了 KV 模型,但它仍然是一颗二叉搜索树,因此整棵树的结构没有发生任何变化。唯一的变化在于树的结点,对与 KV 模型来说,树中的结点不仅要存 Key,还要存 Value,这就进一步导致在插入时不仅要插入 Key,还要插入一个与该 Key 对应的 Value。其次对 KV 模型来说,Key 不允许被修改,Value 可以被修改,因此对 KV 模型来说,在 Find 的时候应该返回结点的指针,这样方便后续进行一些操作。
五、二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。对有 n 个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二插搜索树的深度的函数,即结点越深,则比较次数越多。但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树。

-
最优情况下:二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为: l o g 2 n log2^n log2n。
-
最差情况下:二叉搜索树退化为单支树(或者类似单支),其平均比较次数为: N 2 \frac{N}{2} 2N。如果退化成了单支树,那么二叉搜索树的性能就失去了。此时就需要用到即将登场的 AVL 树和红黑树了。
六、结语
今天的分享到这里就结束啦!如果觉得文章还不错的话,可以三连支持一下,春人的主页还有很多有趣的文章,欢迎小伙伴们前去点评,您的支持就是春人前进的动力!

相关文章:

【C++杂货铺】一颗具有搜索功能的二叉树
文章目录 一、二叉搜索树概念二、二叉搜索树的操作2.1 二叉搜索树的查找2.2 二叉搜索树的插入2.3 二叉搜索树的删除 三、二叉搜索树的实现3.1 BinarySearchTreeNode(结点类)3.2 BinarySearchTree(二叉搜索树类)3.2.1 框架3.2.2 in…...

uni-app使用vue3,在元素或组件实例上添加ref,用this.$refs显示undefined
项目中引用了一个UI组件库,在表单上添加了ref属性,方便提交时验证。触发提交方法时显示不存在这个方法或this.$refs为undefined。 <u--form labelPosition"left" :model"userInfo" :rules"rules" ref"loginForm&…...
蜂蜜配送销售商城小程序的作用是什么
蜂蜜是农产品中重要的一个类目,其受众之广市场需求量大,但由于非人人必需品,因此传统线下门店经营也面临着痛点,线上入驻平台也有很多限制难以打造自有品牌,无法管理销售商品及会员、营销等,缺少自营渠道&a…...

大数据Flink(八十四):SQL语法的DML:窗口聚合
文章目录 SQL语法的DML:窗口聚合 一、滚动窗口(TUMBLE)...
)
系统集成|第十八章(笔记)
目录 第十八章 安全管理18.1 信息安全管理18.2 信息系统安全18.3 物理安全管理18.4 人员安全管理18.5 应用该系统安全管理18.6 信息安全等级保护18.7 拓展 上篇:第十七章、变更管理 下篇:第十九章、风险管理 第十八章 安全管理 18.1 信息安全管理 信息安…...

480万商品,如何架构商品治理平台?
说在前面 在40岁老架构师 尼恩的读者交流群(50)中,很多小伙伴拿高薪,完成架构的升级,进入架构师赛道,打开薪酬天花板。 最近有小伙伴拿到了一线互联网企业如京东、网易、微博、阿里、汽车之家、极兔、有赞、希音、百度、滴滴的架…...

【C++入门指南】C如何过渡到C++?祖师爷究竟对C++做了什么?
【C入门指南】C如何过渡到C?祖师爷究竟对C做了什么? 前言一、命名空间1.1 命名空间的定义1.2 命名空间使用 二、C输入、输出2.1 std命名空间的使用惯例 三、缺省参数3.1 缺省参数的定义3.2 缺省参数分类 四、函数重载4.1 函数重载概念4.2 C支持函数重载的…...
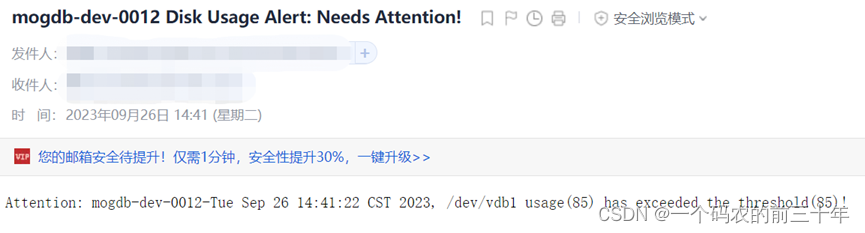
简易磁盘自动监控服务
本文旨在利用crontab定时任务(脚本请参考附件)来监控单个服务节点上所有磁盘使用情况,一旦超过既定阈值则会通过邮件形式告警相关利益人及时介入处理。 1. 开启SMTP服务 为了能够成功接收告警信息,需要邮件接收客户都安开启SMTP服务。简要流程请参考下…...
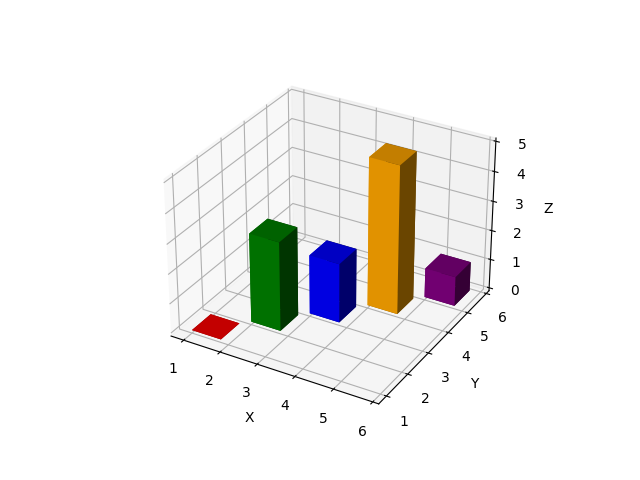
【100天精通Python】Day65:Python可视化_Matplotlib3D绘图mplot3d,绘制3D散点图、3D线图和3D条形图,示例+代码
1 mpl_toolkits.mplot3d 功能介绍 mpl_toolkits.mplot3d 是 Matplotlib 库中的一个子模块,用于绘制和可视化三维图形,包括三维散点图、曲面图、线图等。它提供了丰富的功能来创建和定制三维图形。以下是 mpl_toolkits.mplot3d 的主要功能和功能简介&am…...

十六,镜面IBL--预滤波环境贴图
又到了开心的公式时刻了。 先看看渲染方程 现在关注第二部分,镜面反射。 其中 这里很棘手,与输入wi和输出w0都有关系,所以,再近似 其中第一部分,就是预滤波环境贴图,形式上与前面的辐照度图很相似&#…...
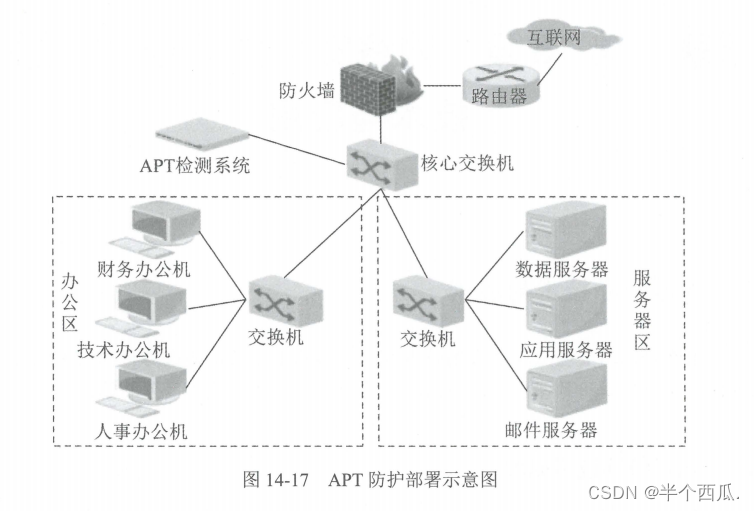
信息安全:恶意代码防范技术原理.
信息安全:恶意代码防范技术原理. 恶意代码的英文是 Malicious Code, 它是一种违背目标系统安全策略的程序代码,会造成目标系统信息泄露、资源滥用,破坏系统的完整性及可用性。 目录: 恶意代码概述: (1&a…...
开源媒体浏览器Kyoo
什么是 Kyoo ? Kyoo 是一款开源媒体浏览器,可让您流式传输电影、电视节目或动漫。它是 Plex、Emby 或 Jellyfin 的替代品。Kyoo 是从头开始创建的,它不是一个分叉。一切都将永远是免费和开源的。 软件特性: 管理您的电影、电视剧…...

人脸解锁设备时出现相机报错
(1)背景分析 这是项目当中实际遇到的问题,如下代码仅用作分析和记录。 现在问题的现象是:刚亮屏大概在2s以内对着人脸一般是能解锁的,但是超过2s之后在对着人脸,是无法解锁成功的。 (2&#…...

【广州华锐互动】利用VR开展工业事故应急救援演练,确保救援行动的可靠性和有效性
在工业生产中,事故的突发性与不可预测性常常带来巨大的损失。传统的应急演练方式往往存在场地限制、成本高、效果难以衡量等问题。然而,随着虚拟现实(VR)技术的快速发展,VR工业事故应急救援演练应运而生,为…...

还不知道数据类岗位的相关技能和职责吗?涤生大数据告诉你(二)
续接上文:还不知道数据类岗位的相关技能和职责吗?涤生大数据告诉你(一) 1.数据治理工程师 工作职责 数据治理工程师的工作职责主要包括以下几个方面: 1. 数据管理策略制定:制定和实施数据管理策略&#…...
常见应用层协议
一.HTTP(超文本传输协议) HTTP 和 HTTPS 二.FTP(文件传输协议) 三.SMTP(简单邮件传输协议) 四.POP3(邮局协议版本3) 五.IMAP(互联网消息访问协议) 六.DNS&am…...

解决docker容器无法关闭的问题
一般正常关闭: docker stop 容器ID解决方法 方法1:强制停止docker kill 容器ID方法2:直接重启dockersudo service docker stop方法3:直接删除容器,重新创建docker rm -f my_container...

2023-09-27 LeetCode每日一题(餐厅过滤器)
2023-09-27每日一题 一、题目编号 1333. 餐厅过滤器二、题目链接 点击跳转到题目位置 三、题目描述 给你一个餐馆信息数组 restaurants,其中 restaurants[i] [idi, ratingi, veganFriendlyi, pricei, distancei]。你必须使用以下三个过滤器来过滤这些餐馆信息…...

梯度下降法(SGD)原理
目录 梯度下降法(SGD)原理:求偏导 1. 梯度(在数学上的定义) 2. 梯度下降法迭代步骤 BGD批量梯度下降算法 BGD、SGD在工程选择上的tricks 梯度下降法(SGD)原理:求偏导 1. 梯度(在数学上的定义) 表示某一函数在该点处的方向导数沿着该方向取得最大值…...

QQ表情包存储位置解析
一些常见的设备和系统的QQ表情包存储位置: Windows系统: 路径:C:\Users[用户名]\Documents\Tencent Files[QQ号码]\Image\Image\CustomFace 在这个文件夹中,您可以找到所有自定义的QQ表情包。 Android系统: 路径&am…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...
