面试 | 递归乘法【细节决定成败】

不用[ * ]如何使两数相乘❓
- 一、题目明细
- 二、思路罗列 & 代码解析
- 1、野蛮A * B【不符合题意】
- 2、sizeof【可借鉴】
- 解析
- 3、简易递归【推荐】
- ① 解析(递归展开图)
- ② 时间复杂度分析
- 4、移位<<运算【有挑战性💪】
- ① 思路顺理
- ② 算法图解
- ③ 代码分析
- ④ 调试分析
- 📺视频解说
- 三、总结与提炼
一、题目明细
原题传送门

- 可能有读者会说为什么那么简单的题目也要写个题解?
- 答:【细节决定成败,不可忽视细枝末节】,对算法题的思考尽量要做到多维度考虑、多思考,继而找出最优解👑
二、思路罗列 & 代码解析
下面会列出我所AC的所有解,有些可能不符合题意
1、野蛮A * B【不符合题意】
本以为不让使用【*】运算符,但是试了一下,竟然也可以过😮
int multiply(int A, int B){return A * B;
}

2、sizeof【可借鉴】
这个方法我觉得还是比较巧妙,如果题目没有指定说要使用递归来进行求解,可以考虑
int multiply(int A, int B){char a[A][B];return sizeof(a);
}

解析
- 有很多学习完C语言的同学在使用
sizeof()的时候都会觉得它是一个函数,但真的是吗?其实可以去cpluplus中看看。就可以观测到无论是搜索多久都不会有结果

- 其实对于
sizeof()来说是一个操作符,而且是一个单目操作符,如果不清楚的可以看看我的操作符汇总大全。用来计算某一个数据类型的变量所占的字节大小。不要和Pascal中的sizeof()混淆了,在这门语言中是作为【函数】来看待的
在 Pascal 语言中,sizeof() 是一种内存容量度量函数,功能是返回一个变量或者类型的大小(以字节为单位);在 C语言中,sizeof() 是一个判断数据类型或者表达式长度的运算符《来源于百度百科》
- 所以在这道题中,其实我们利用两数相乘的这个逻辑,去定义一个字符型的二维数组,然后将这个数组当做是长方体,那对于长方体的面积来说就是
长 * 宽,那对于二维数组这个矩阵来说其实就是去计算它在内存中所占地字节数是多少,这样就可以很轻易地想到使用sizeof()去进行求解 - 这里要注意的是需定义为【字符数组】,因为
char类型的变量在内存中只占一个字节,若是定义为整型数组,算出来就是结果的4倍了!

3、简易递归【推荐】
这才是最符合题意的做法,使用递归去进行求解
class Solution {
public:int Mul(int big, int small){if(small == 0) return 0; //与0相乘一定为0if(small == 1) return big; //与1相乘一定为自身return big + Mul(big, small - 1); //small个big相加,small递减}int multiply(int A, int B) {//首先区分两者中的大的那个和小的那个int big = A > B ? A : B;int small = A < B ? A : B;return Mul(big, small);}
};

① 解析(递归展开图)
递归对有些同学来说可能不好理解,因此讲说一下代码逻辑
- 首先题目说到,两个数相乘不可以使用【*】号,那其实我们其看一下两个数相乘的原理也就是从加法转化过来的,
例1:3 * 4 == 4 + 4 + 4 | 例2:2 * 5 == 5 + 5 - 选取到小的那个数作为相加的次数
- 选取大的那个数作为相加的数字
- 在递归的函数中,若是发现
small == 0,那直接return 0即可,因为任何数和0相乘都是0 - 若是发现
small == 1,那就直接返回big,因为任何数和1相乘都是1 - 若是都不满足,则进行递归调用,注意要保留当前层的big,然后再产生递归让
small - 1即可
若是感觉有点抽象的话,就通过递归展开图来看看吧

② 时间复杂度分析
- 对于上面这种方法的时间复杂度为
O(N)。准确点来说是O(small),相当于一个线性阶。如果对时间复杂度如何计算不是很懂,可以看看我的这篇文章——> 时间与空间复杂度就看这篇了 - 那有没有更优的方法呢?就来看看下面这种吧
4、移位<<运算【有挑战性💪】
若是你搞懂了上面这种方法,那便来看看这种
移位<<这种方法吧,会让你更上一层楼
int Mul(int big, int small)
{if(small == 0) return 0;if(small == 1) return big;int half_small = small >> 1; //右移运算符,每次使small缩小一半//递归算出每一半的乘积int half_Sum = Mul(big, half_small); //判断每一层的递归中的small为偶数还是奇数if(small % 2 == 0){return half_Sum + half_Sum; //若为偶数直接是double倍}else{return half_Sum + half_Sum + big; //若为奇数则还需加上一个big}
}int multiply(int A, int B){//1.划分二者的大小int big = A > B ? A : B;int small = A < B ? A :B;int ret = Mul(big, small);return ret;
}

① 思路顺理
- 首先对于主接口函数还是一样,区分两者中谁大谁小,然后传入递归函数中
- 在递归函数中,我的思路是这样的,既然在上一题中想到了
线性阶,那便想要优化为对数阶,那对于对数阶而言一定存在一个二分的关系,然后就可以想到一半的关系 - 所以对于small个big相乘,其实并不需要加small次,加
small/2次即可,对于small/2次,其实也只需要加small/2次即可,那么这就相当于是一个递归的问题,要求出8个10的和,先求出4个10的和;要求出4个10的和,先求出2个10的和,要求出2个10的和,就先求出1个10,最后再进行层层回调,便可以算出small个big的和为多少了 - 不过这个small的情况还是判断其为奇数还是偶数:对于偶数来说就是一个二分,但是对于奇数来说就不一样了,因为÷2之后相当于是一个整除,
所以会漏掉一次的big相加,要在求当前和的最后加上一个big - 对于上述这种算法的时间复杂度很明显可以看出来是O(log2small)
② 算法图解
经过思路的讲解与分析,可能你还有些云里雾里😵那就通过算法分解图来看看吧
- small为偶数的情况

- small为奇数的情况

③ 代码分析
通过算法图的展示之后,相信你一定很清楚该如何去解决这个问题了,我们再来回顾一下代码
- 若是small进来直接为0,那么直接
return 0便可
if(small == 0) return 0;
- 这句便是算出当前层small的一半为多少,使用的便是移位运算符,
右移是缩小1/2
int half_small = small >> 1; //右移运算符,每次使small缩小一半
- 求出当前层small的一半之后,就继续进行递归,
//递归算出每一半的乘积
int half_Sum = Mul(big, half_small);
- 若是当递归调用的时候
small == 1了,便return big进行回调
if(small == 1) return big;
- 在回调之后,便会进行当前层一半总数的计算,这里就是我说的要对small进行奇偶数分类的情况
//判断每一层的递归中的small为偶数还是奇数
if(small % 2 == 0){return half_Sum + half_Sum; //若为偶数直接是double倍
}else{return half_Sum + half_Sum + big; //若为奇数则还需加上一个big
}
④ 调试分析
通过调试再来看看程序到底是如何运行的
- 以
big = 6, small = 4为例,进到递归函数中

- 通过右移运算符
>>便算出small的一半

- 继续递归,直到
small == 1为止

- 此时small便为1,执行
return big

- 递归回来之后便计算当前层的总和,因为
small == 2为偶数所以无需再加上big

- 此时继续回调,算出
small == 4这一层的总和

- 最后便通过递归计算出了【4 * 6】的和为24

为了更好地对照算法图,也来测试一下奇数的情况
- 这次的对比是运算是
big = 8, small = 6

- 可以看到,出现了
small为奇数的情况

- 继续递归,直到
small == 1为止

- 然后开始计算每一层的总和,注意:回到
small == 3的递归层时,要进入第二个if分支

- 此时就需要加上整除之后遗漏的那个big了

- 回到
small == 6的递归层时继续计算当前层的总和

- 最后就算出了
6 * 8 = 48的结果

📺视频解说
本文的题解都是通过看下面这位UP主写出来的,可以看看他的讲解——> 主页
leetcode 面试题 08.05. 递归乘法
三、总结与提炼
最后来总结一下本文所学习的内容📖
- 【递归乘法】这道题是LeetCode上的一道面试题,虽然题目看起来比较简单,但是递归对很多同学来说还是比较困难,所以我在这里做一个细致的讲解
- 主要是详细解说了有关递归的两种解法,对于简易递归来说就是本题的答案,但是我们要像在面试中胜出,就必须要想到更好、更优的解法;对于第二种
sizeof的解法,可供读者参考,也是比较巧妙的方法,不过要清楚sizeof是一个操作符,而不是一个函数
学会不断思考,不断突破自己,才是最大的进步

相关文章:

面试 | 递归乘法【细节决定成败】
不用[ * ]如何使两数相乘❓一、题目明细二、思路罗列 & 代码解析1、野蛮A * B【不符合题意】2、sizeof【可借鉴】解析3、简易递归【推荐】① 解析(递归展开图)② 时间复杂度分析4、移位<<运算【有挑战性💪】① 思路顺理② 算法图解…...
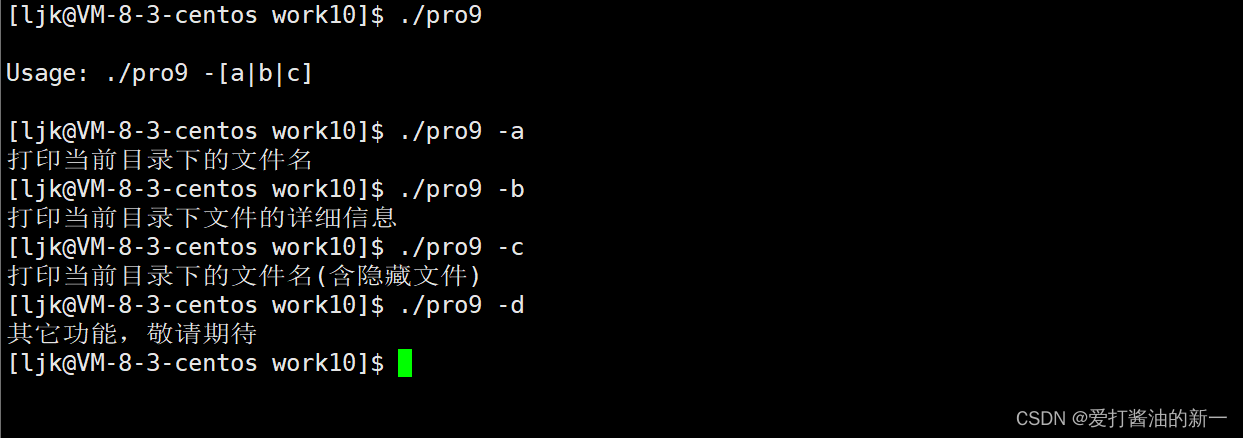
【Linux】环境变量与进程优先级
文章目录🎪 进程优先级🚀1.孤儿进程🚀2.优先级查看🚀3.优先级修改🎪 环境变量🚀1.常见环境变量🚀2.环境变量获取🚀3.main中的命令行参数🎪 进程优先级 每个进程都有相应…...
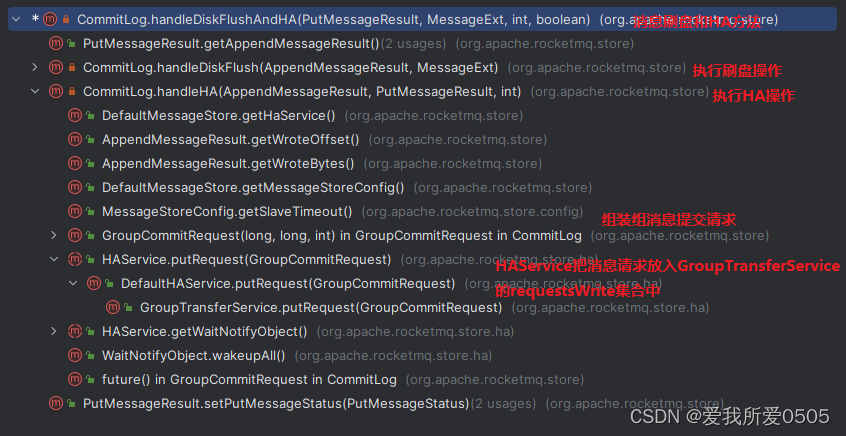
RocketMQ5.0.0的Broker主从同步机制
目录 一、主从同步工作原理 1. 主从配置 2. 启动HA 二、主从同步实现机制 1. 从Broker发送连接事件 2. 主Broker接收连接事件 3. 从Broker反馈复制进度 4. ReadSocketService线程读取从Broker复制进度 5. WriteSocketService传输同步消息 6. GroupTransferService线程…...

深度学习论文: EdgeYOLO: An Edge-Real-Time Object Detector及其PyTorch实现
深度学习论文: EdgeYOLO: An Edge-Real-Time Object Detector及其PyTorch实现 EdgeYOLO: An Edge-Real-Time Object Detector PDF: https://arxiv.org/pdf/2302.07483.pdf PyTorch代码: https://github.com/shanglianlm0525/CvPytorch PyTorch代码: https://github.com/shangli…...
如何做好APP性能测试?
随着智能化生活的推进,我们生活中不可避免的要用到很多程序app。有的APP性能使用感很好,用户都愿意下载使用,而有的APP总是出现卡顿或网络延迟的情况,那必然就降低了用户的好感。所以APP性能测试对于软件开发方来说至关重要&#…...
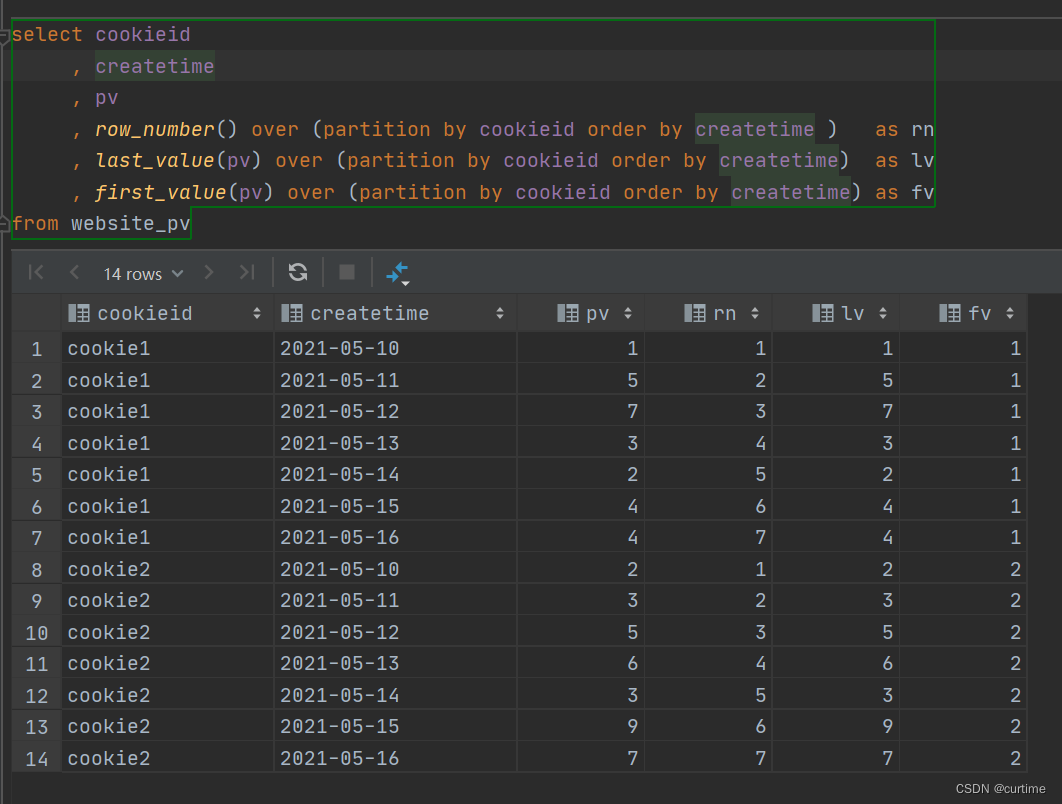
Hive窗口函数
概述 窗口函数(window functions)也叫开窗函数、OLAP函数。 如果函数具有over子句,则它是窗口函数 窗口函数可以简单地解释为类似于聚合函数的计算函数,但是通过group by 子句组合的 常规聚合会隐藏正在聚合的各个…...
:在默认构造函数内部使用带参数的构造函数)
C++学习笔记(1):在默认构造函数内部使用带参数的构造函数
题目以下代码的输出是不是0:#include <unordered_map> #include <iostream>using namespace std;struct CLS{int i;CLS(int i_) :i(i_){}CLS(){CLS(0);} };int main(){CLS obj;std::cout << obj.i << endl;return 0; }结果-858993460为什么…...
设计模式源码案例)
Android面试题_安卓面经(23/30)设计模式源码案例
系列专栏: 《150道安卓常见面试题全解析》 安卓专栏目录见帖子 : 安卓面经_anroid面经_150道安卓基础面试题全解析 安卓系统Framework面经专栏:《Android系统Framework面试题解析大全》 安卓系统Framework面经目录详情:Android系统面经_Framework开发面经_150道面试题答案解…...

Dubbo性能调优参数以及原理
Dubbo作为一个服务治理框架,功能相对来说比较完善,性能也挺不错。但很多同学在使用dubbo的时候,只是简单的参考官方说明进行配置和应用,并没有过多的去思考一些关键参数的意义,最终做出来的效果总是差强人意,接下来我们…...
)
vue3全家桶之vuex和pinia持久化存储基础(二)
一.vuex数据持久化存储 这里使用的是vuex4.1.0版本,和之前的vuex3一样,数据持久化存储方案也使用 vuex-persistedstate,版本是最新的安装版本,当前可下载依赖包版本4.1.0,接下来在vue3项中安装和使用: 安装vuex-persistedstate npm i vuex-persisteds…...
LAMP架构与搭建论坛
目录 1、LAMP架构简述 2、各组件作用 3、构建LAMP平台 1.编译安装Apache httpd服务 2.编译安装mysql 3.编译安装php 4.搭建一个论坛 1、LAMP架构简述 LAMP架构是目前成熟的企业网站应用模式之一,指的是协同工作的一整台系统和相关软件,能够提供动…...

代码随想录 || 回溯算法93 78 90
Day2493.复原IP地址力扣题目链接给定一个只包含数字的字符串,复原它并返回所有可能的 IP 地址格式。有效的 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 . 分隔。例如&#…...
界面组件Kendo UI for Angular——让网格数据信息显示更全面
Kendo UI致力于新的开发,来满足不断变化的需求,通过React框架的Kendo UI JavaScript封装来支持React Javascript框架。Kendo UI for Angular是专用于Angular开发的专业级Angular组件,telerik致力于提供纯粹的高性能Angular UI组件,…...
【Linux】进程状态|优先级|进程切换|环境变量
文章目录1. 运行队列和运行状态2. 进程状态3. 两种特殊的进程僵尸进程孤儿进程4. 进程优先级5. 进程切换进程特性进程切换6. 环境变量的基本概念7. PATH环境变量8. 设置和获取环境变量9. 命令行参数1. 运行队列和运行状态 💕 运行队列: 进程是如何在CP…...
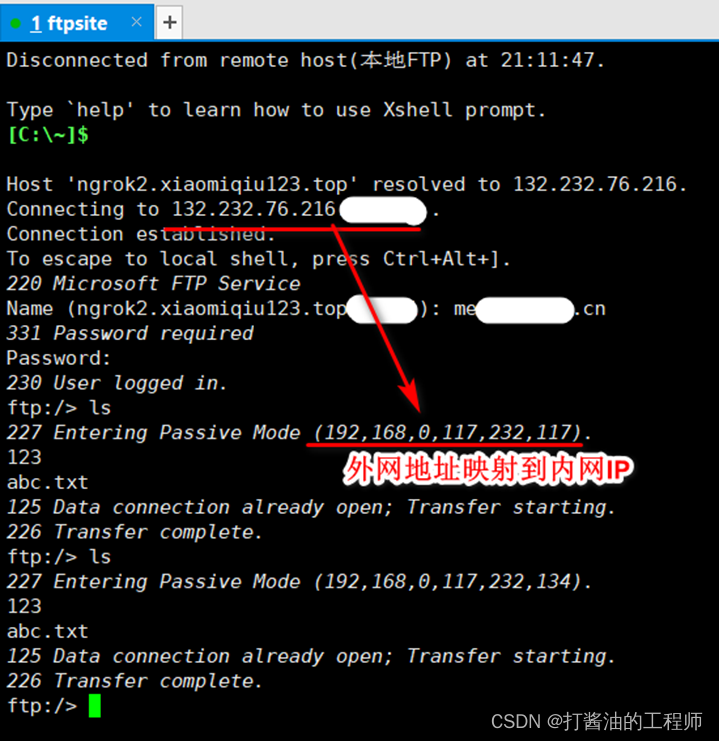
合宙Air780E|FTP|内网穿透|命令测试|LuatOS-SOC接口|官方demo|学习(18):FTP命令及应用
1、FTP服务器准备 本机为win11系统,利用IIS搭建FTP服务器。 搭建方式可参考博文:windows系统搭建FTP服务器教程 windows系统搭建FTP服务器教程_程序员路遥的博客-CSDN博客_windows服务器安装ftp 设置完成后,测试FTP(已正常访问…...
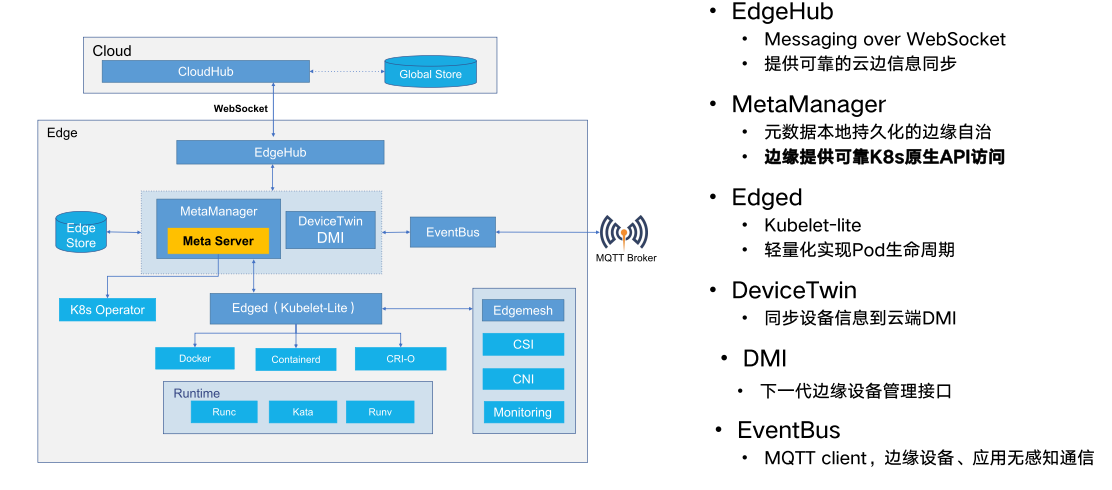
大规模 IoT 边缘容器集群管理的几种架构-4-Kubeedge
前文回顾 大规模 IoT 边缘容器集群管理的几种架构-0-边缘容器及架构简介大规模 IoT 边缘容器集群管理的几种架构-1-RancherK3s大规模 IoT 边缘容器集群管理的几种架构-2-HashiCorp 解决方案 Nomad大规模 IoT 边缘容器集群管理的几种架构-3-Portainer 📚️Reference…...

Spring底层核心原理解析
Spring简介 ClassPathXmlApplicationContext context new classPathXmlApplicationContext("spring.xml"); UserService userService (UserService) context.getBean("userService"); userService.test();上面一段代码是我们开始学习spring时看到的&…...
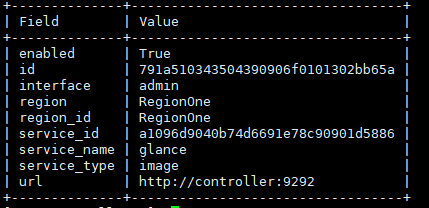
OpenStack手动分布式部署Glance【Queens版】
目录 Glance简介 1、登录数据库配置(在controller执行) 1.1登录数据库 1.2数据库里创建glance 1.3授权对glance数据库的正确访问 1.4退出数据库 1.5创建glance用户密码为000000 1.6增加admin角色 1.7创建glance服务 1.8创建镜像服务API端点 2、安装gla…...

谈一谈你对View的认识和View的工作流程
都2023年了,不会还有人不知道什么是View吧,不会吧,不会吧。按我以往的面试经验来看,View被问到的概率不比Activity低多少哦,个人感觉View在Android中的重要性也和Activity不相上下,所以这篇文章将介绍下Vie…...

Redis集群的脑裂问题
集群脑裂导致数据丢失怎么办? 什么是脑裂? 先来理解集群的脑裂现象,这就好比一个人有两个大脑,那么到底受谁控制呢? 那么在 Redis 中,集群脑裂产生数据丢失的现象是怎样的呢? 在 Redis 主从架…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

Linux操作系统共享Windows操作系统的文件
目录 一、共享文件 二、挂载 一、共享文件 点击虚拟机选项-设置 点击选项,设置文件夹共享为总是启用,点击添加,可添加需要共享的文件夹 查询是否共享成功 ls /mnt/hgfs 如果显示Download(这是我共享的文件夹)&…...
