HDLBits-Edgedetect
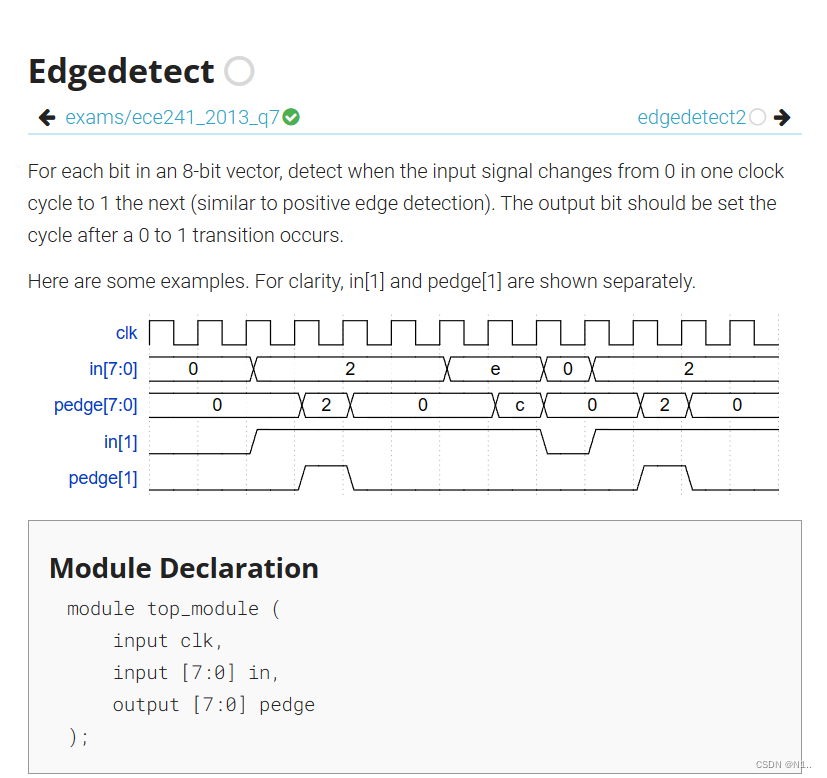 刚开始写的代码如下:
刚开始写的代码如下:
module top_module (input clk,input [7:0] in,output [7:0] pedge
);reg [7:0] in_pre;always @(posedge clk)begin in_pre <= in;endassign pedge = in & ~in_pre;
endmodule
但是提交结果是错误的。猜想原因如下:
assign pedge = in&~in_pre; 表明通过一个门 将in 与 in_pre处理后 输出连接到pedge,那么只要in 或者 in_pre发生变化,那么 pedge结果就会立即发生变化。
但是该题的思路是通过一个寄存器,将输入延迟保存一个周期,通过检测现在的输入和上一周期的输入即可判断是否有上升沿。因此 ,应该将 pedge的赋值语句写在 always @(posedge clk)中,那么,每当一个周期,in_pre发生变化时, 才对pedge进行更改。
以下是正确的代码:
module top_module (
input clk,
input [7:0] in,
output [7:0] pedge
);
reg [7:0] in_pre;
always @(posedge clk)begin
in_pre <= in;
pedge <= in & ~in_pre;
end
endmodule
相关文章:

HDLBits-Edgedetect
刚开始写的代码如下: module top_module (input clk,input [7:0] in,output [7:0] pedge );reg [7:0] in_pre;always (posedge clk)begin in_pre < in;endassign pedge in & ~in_pre; endmodule但是提交结果是错误的。猜想原因如下: assign p…...
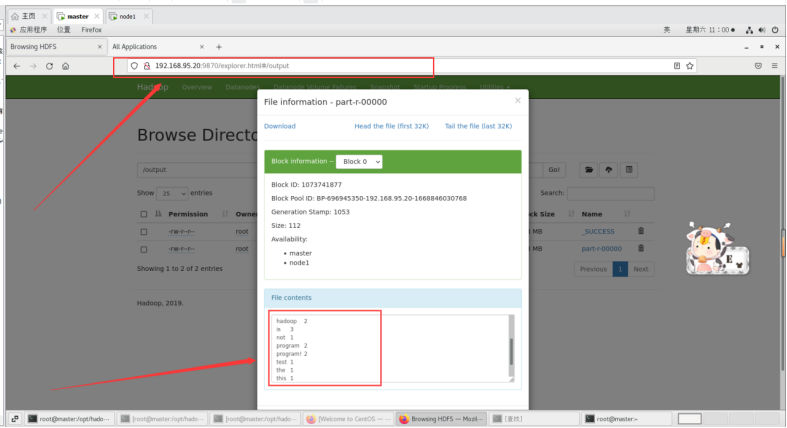
云计算与大数据——部署Hadoop集群并运行MapReduce集群(超级详细!)
云计算与大数据——部署Hadoop集群并运行MapReduce集群(超级详细!) Linux搭建Hadoop集群(CentOS7hadoop3.2.0JDK1.8Mapreduce完全分布式集群) 本文章所用到的版本号: CentOS7 Hadoop3.2.0 JDK1.8 基本概念及重要性 很多小伙伴部署集群用hadoop用mapr…...
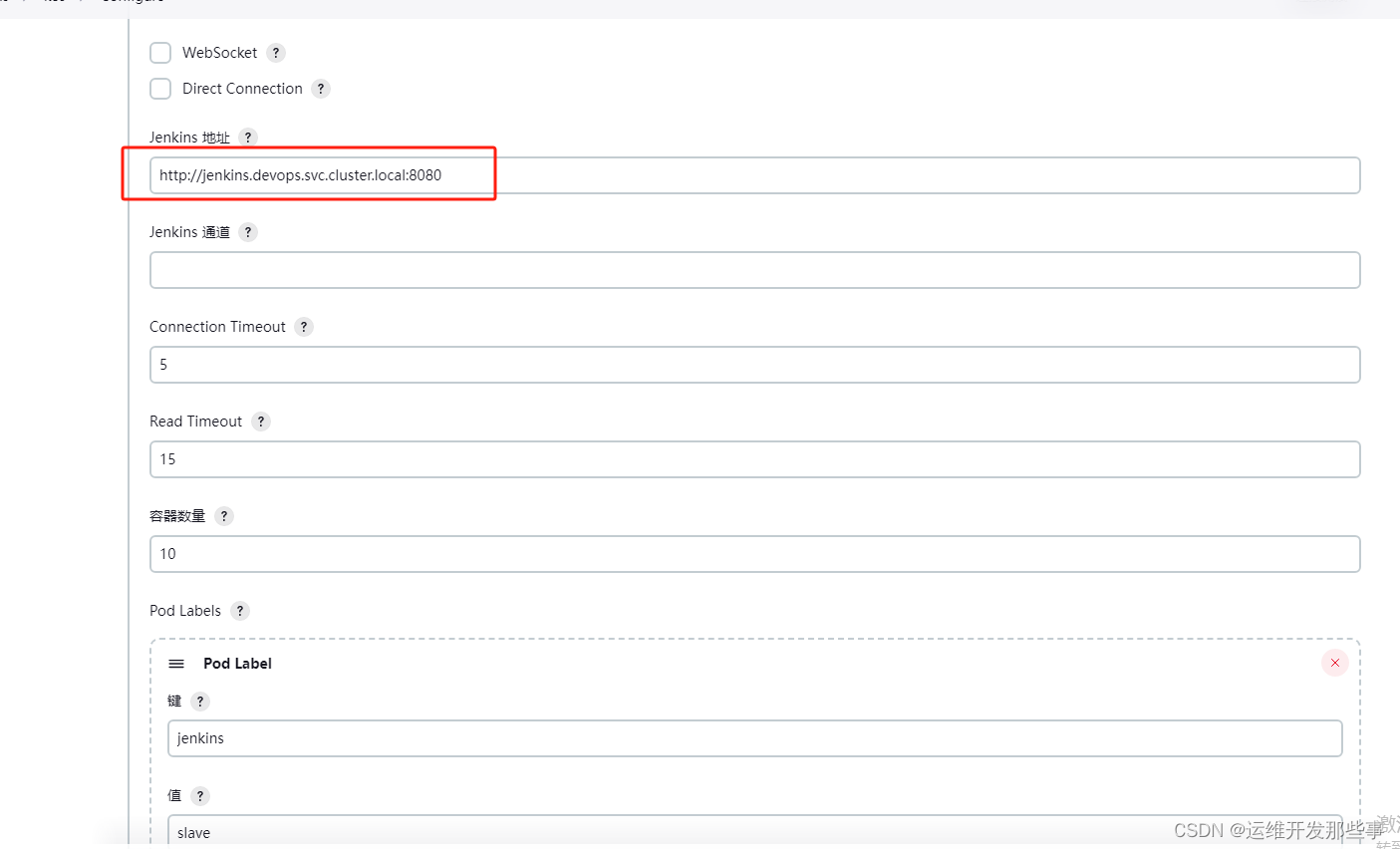
基于jenkins+k8s实现devops
1、背景 由于jenkins运行在k8s上能够更好的利用动态agent进行构建。所以写了个部署教程,亲测无坑 2、部署 1、创建ns kubectl create namespace devops 2、kubectl apply -f jenkins.yml apiVersion: v1 kind: ServiceAccount metadata:name: jenkinsnamespace…...
一文了解企业如何实现文件自动化实时同步
在当今的数字化时代,数据是企业的核心资产,也是企业竞争力的重要体现。数据的传输、共享、协作、备份等都需要依赖文件同步技术,实现数据在不同平台和设备之间的一致性和可用性。文件同步是指将一个或多个文件夹中的内容复制或更新到另一个或…...

低代码系统哪里好
低代码作为近些年来被热议的话题,一直备受争议。低代码的出现更多的是用来辅助那些没有太多技能的人士而使用,在某些方面依然需要强大的代码来解决生产革新。所以低代码也不是浑水猛兽,也需要根据实际情况加以利用。那么为什么低代码会收到如…...
C#WPF通知更改公共类使用实例
本文实例演示C#WPF通知更改公共类使用实例,通过使用公共类简化了代码。其中的代码中也实现了命令的用法。 定义: INotifyPropertyChanged 接口:用于向客户端(通常是执行绑定的客户端)发出某一属性值已更改的通知。 首先创建WPF项目,添加按钮和文本控件 <Window x:C…...

解决高并发问题
在处理项目中的高并发问题时,可以采取以下几种方法: 后端处理:大部分的高并发处理是在后端进行的。可以通过优化数据库查询、增加缓存机制(如集成Redis)、使用分布式技术(如分布式缓存、分布式锁ÿ…...
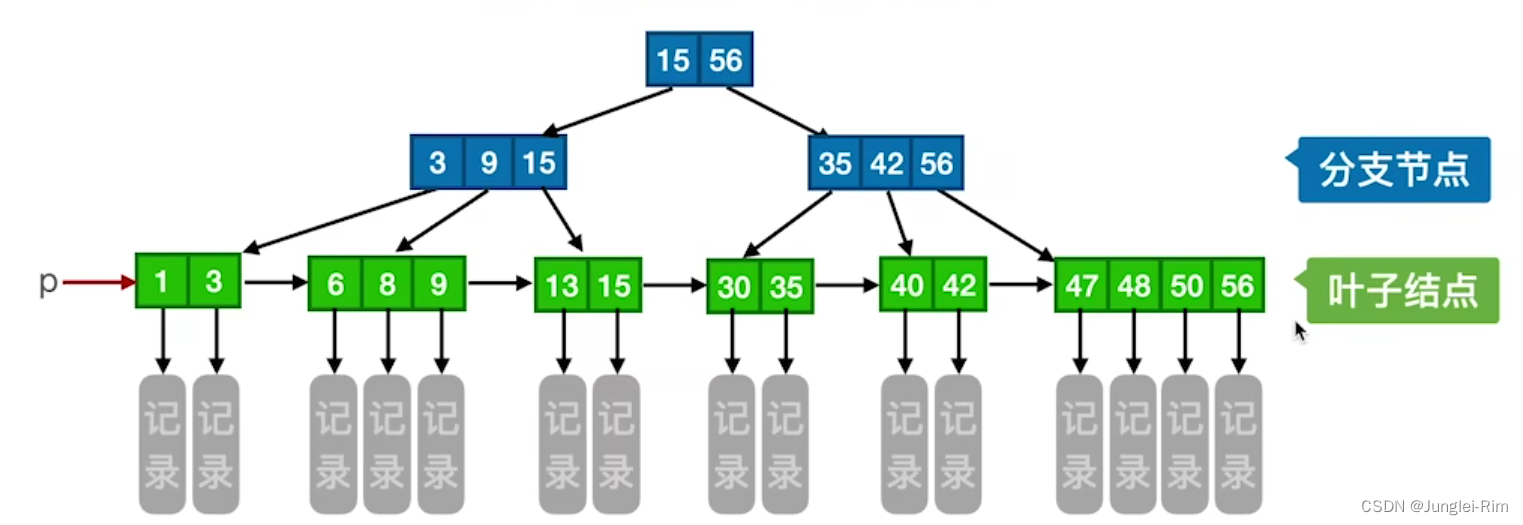
B+树的定义以及查找
1.B树的定义 一棵m阶的B树需满足下列条件: 每个分支结点最多有m棵子树(孩子结点)。非叶根结点至少有两棵子树,其他每个分支结点至少有「m/2]棵子树。结点的子树个数与关键字个数相等。所有叶结点包含全部关键字及指向相应记录的指针,叶结点中将关键字按…...
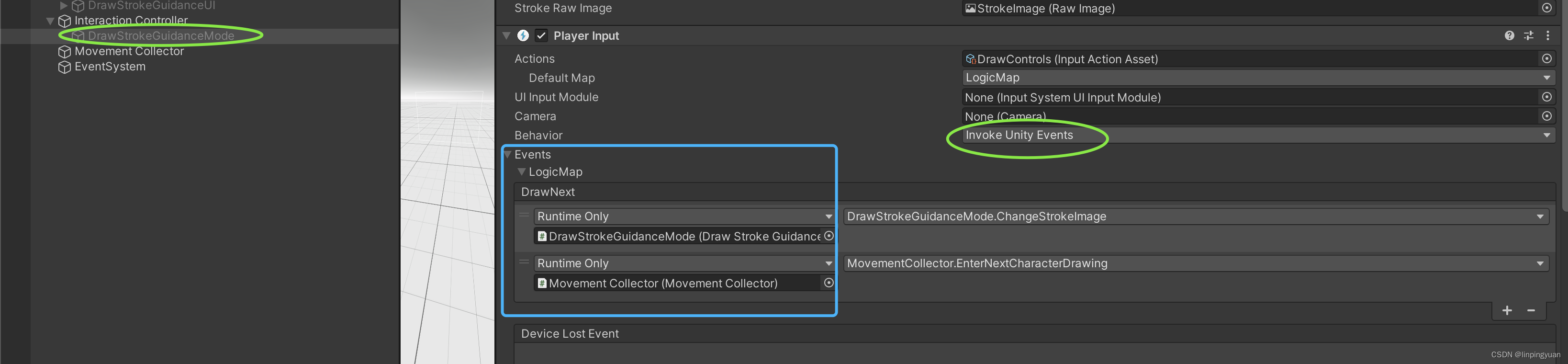
InputAction的使用
感觉Unity中InputAction的使用,步步都是坑。 需求点介绍 当用户长按0.5s 键盘X或者VR left controller primaryButton (即X键)时,显示下一个图片。 步骤总览 创建InputAction资产将该InputAction资产绑定到某个GameObject上在对应的script中…...

Bug排查思路
遇到一个Bug,怎么排查?以下几个思路,希望能对大家有所启发 一、环境问题 1、开发的代码是否已更新 2、是否是缓存原因导致的(强刷,手动清除缓存,web甚至可以直接用无恒模式查看页面) 3、是否…...
独立站引流,如何在Reddit进行营销推广?
Reddit是目前最被忽视却最具潜力的社交媒体营销平台之一,它相当于国内的百度贴吧,是美国最大的论坛,也是美国第五大网站,流量仅次于Google、Youtube、Facebook以及亚马逊。 如果会玩,Reddit也可以跟其他的社交媒体营销…...

文件拖拽上传功能已经烂大街了,你还不会吗?
说在前面 🖼文件拖拽上传功能现在已经随处可见,大家应该都用过了吧,那么它具体是怎么实现的大家有去了解过吗?今天我们一起来实现一下这个功能,并封装一个拖拽上传组件吧。 效果展示 体验地址:http://jyeon…...
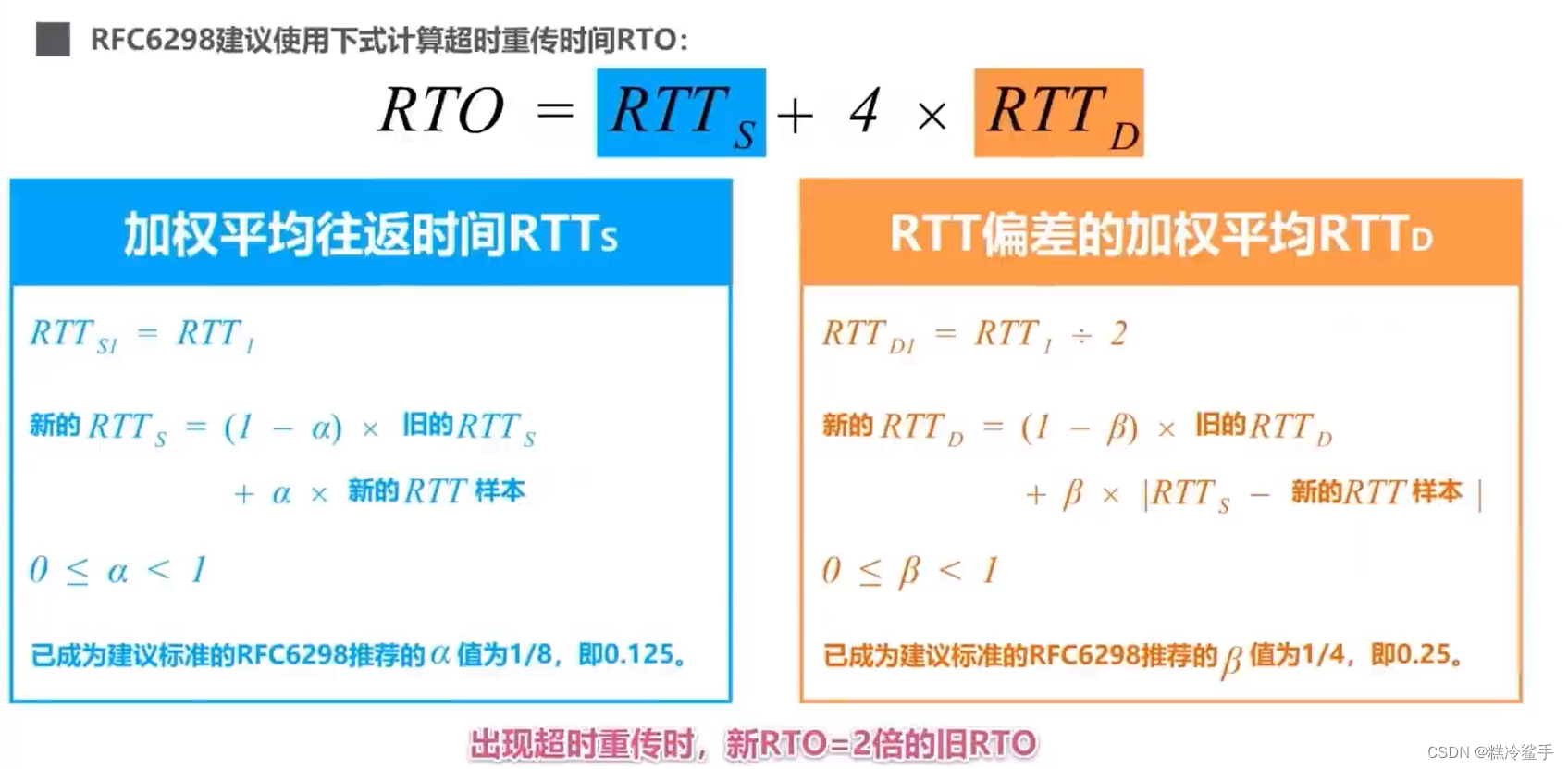
TCP与UDP协议详解!!!
TCP/IP运输层中的两个重要协议 TCP的报文结构 TCP的流量控制 流量控制:让发送方发送速率不要太快,TCP协议使用滑动窗口实现流量控制。 利用滑动窗口机制可以很方便地在TCP连接上实现对发送方的流量控制。 TCP接收方利用自己的接收窗口的大小来限制发送…...

《C++ primer》练习6.36-6.38:书写返回数组引用的函数声明
最近看C primer,看到《C primer》6.3.3练习,要求书写返回数组引用的函数声明,觉得有必要实践记录一下。 这里先总结返回数组的引用的的函数声明写法(下面的Type是数组元素的类型,可以是int、float等,如果要…...
——过滤器)
Spring Cloud Gateway快速入门(三)——过滤器
文章目录 前言Gateway内置网关过滤器什么是网关过滤器Gateway内置网关过滤器GlobalFilterPreFilterPostFilter 使用示例 Gateway全局网关过滤器什么是全局网关过滤器使用全局网关过滤器注册全局网关过滤器使用全局网关过滤器 全局网关过滤器和Gateway内置网关过滤器的区别1. 注…...

vue3相比vue2的优点
一、响应式: (1)vue2:内置的Object.defineProperty将data中的数据转化成响应式数据的,它会将data中的每个属性都转换为具有getter和setter的响应式属性 Object.defineProperty是一个内置的方法,它用于定义…...
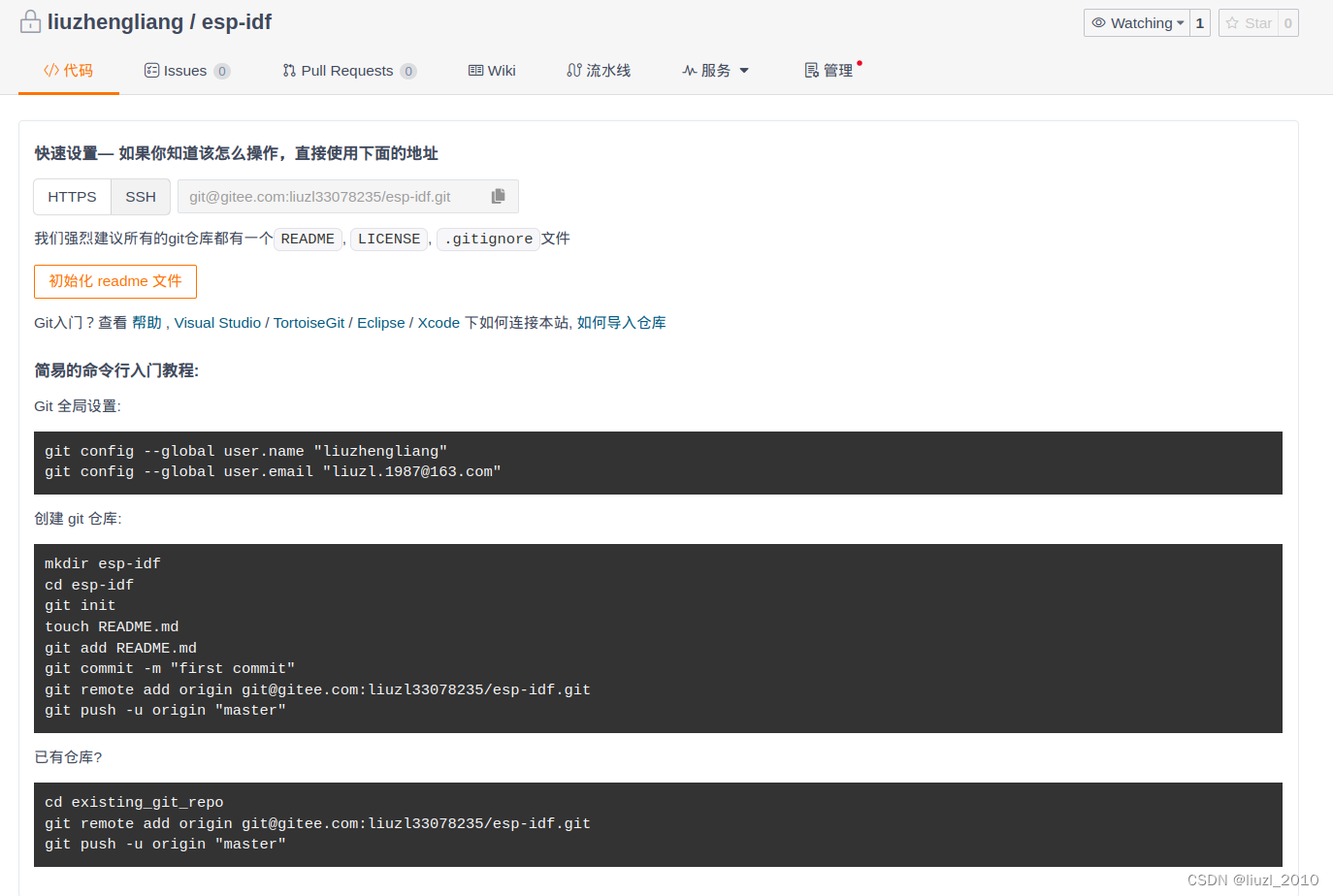
gitee-快速设置
快速设置— 如果你知道该怎么操作,直接使用下面的地址 HTTPS SSH: gitgitee.com:liuzl33078235/esp-idf.git 我们强烈建议所有的git仓库都有一个README, LICENSE, .gitignore文件 初始化 readme 文件 Git入门?查看 帮助 , Visual Studio / TortoiseG…...
将切分的图片筛选出有缺陷的
将切分的图片筛选出有缺陷的 需求代码 需求 由于之前切分的图像有一些存在没有缺陷,需要再次筛选 将可视化的图像更改后缀 更改为xml的 可视化代码 可视化后只有7000多个图像 原本的图像有1W多张 代码 # 按照xml文件删除对应的图片 # coding: utf-8 from P…...

el-tooltip内容换行显示
效果图: html: <div class"rules-tooltip flex-center"><el-tooltip class"item" effect"dark" placement"bottom-start"><div slot"content" v-html"tipsContent"></div>&l…...

linux 下用posix semaphore 解决资源竞争问题实例
/* author: hjjdebug date: 2023年 09月 20日 星期三 09:33:58 CST description: 10辆汽车通过承重5辆汽车的桥,处理一个资源争用问题 * 10个线程代表10辆汽车 * 桥上只能承载5辆汽车, 代表最大只能同时有5辆汽车通过 概要: 让10个线程竞争5个资源,用posix 接口, sem…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...
