【图论C++】树的重心——教父POJ 3107(链式前向星的使用)
》》》算法竞赛
/*** @file * @author jUicE_g2R(qq:3406291309)————彬(bin-必应)* 一个某双流一大学通信与信息专业大二在读 * * @brief 一直在竞赛算法学习的路上* * @copyright 2023.9* @COPYRIGHT 原创技术笔记:转载需获得博主本人同意,且需标明转载源* @language C++* @Version 1.0还在学习中 */
- UpData Log👆 2023.9.26 更新进行中
- Statement0🥇 一起进步
- Statement1💯 有些描述是个人理解,可能不够标准,但能达其意
技术提升站点
文章目录
- 》》》算法竞赛
- 技术提升站点
- 21 树上问题
- 21-0 关于 树 的问题 有哪些?
- 21-1 树的重心
- 21-1-1 重心是什么?
- 21-1-2 重心的性质
- 21-1-2 重心的查找
- 教父(poj 3107)
21 树上问题
树是图的一种特例,树就是 “没有环” 的连通图
判断一个 图 是否是一个 树,需要满足的条件:
-
1)树根:一棵树可以基于
无向图与有向图,区别在于树根。基于无向图的树(无根树),是没有固定树根的(也就是说树根的个数可能不止为1,或说每个结点都能做为树根)
基于有向图的树(有根树),有且仅有一个树根
-
2)父节点与子节点的关系:每个节点有且仅有一个父节点。从根节点遍历,必须由父节点遍历到子节点
-
3)连通性:从 根 出发可以遍历树上所有(除根节点外)节点,且到这些节点的路径只有一条
有根树 与 有向无环图 DAG 的 区别
有向无环图:不能从某点开始经过数点回到该点
有根树 都是 DAG,DAG 不一定是 有根树(如下图:虽然没有构成环,但是4号节点同时拥有两个父节点,不符合有根树的定义)
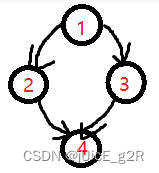
21-0 关于 树 的问题 有哪些?
直通车:
- 树的判断:判定 图 是否为 树 的方法是 DFS遍历
- 树的存储:与 图 的存储方式一致(链式前向星)
- 树的路径问题(包含了 查找最近公共祖先
LCA):点击直通 树的路径问题 - 树的直径
- 树的重心(下文将讲解)
- 多叉树、二叉树
- 树上前缀和,树上差分
21-1 树的重心
21-1-1 重心是什么?
树的重心适用在无根树(一个不含回路的无向图)树的重心是 以任意结点 u 为根 计算它最大子树的节点数 n o d e n node_n noden,如果u节点的 n o d e n node_n noden 最少,则u节点为 树的重心。
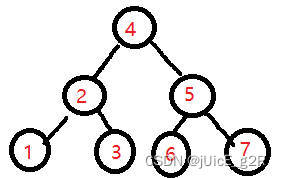
可以一眼看出:4号结点 就是 树的重心,因为这个点能满足 n o d e n node_n noden 是最小的(左子树{4,2,1,3,}:4个,右子树{4,5,6,7}:4个),而其他任意一个节点的子树(例如 2号节点的最大子树{2,4,5,6,7}5个)都是比这个点的最大子树的节点数是大的。
21-1-2 重心的性质
- 以树的重心为根时,所有子树的大小都不超过整棵树大小的一半。(树上分治会用到)
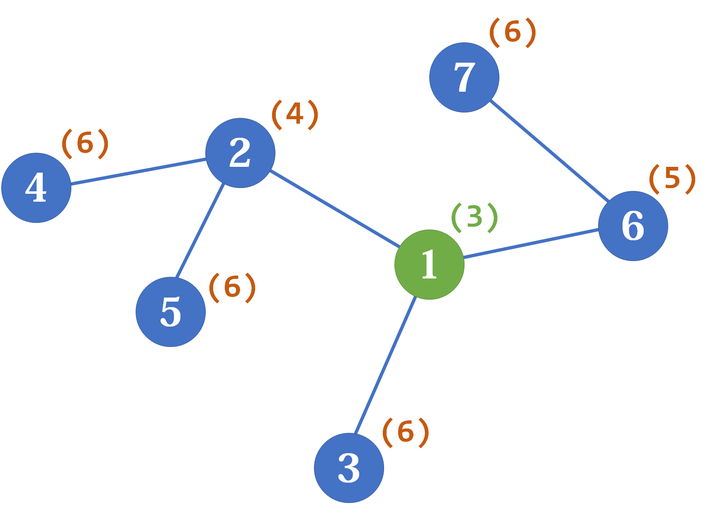
- 树的重心如果不唯一,则至多有两个,且这两个重心相邻。

- 树中所有点到某个点的距离和中,到重心的距离和是最小的;如果有两个重心,那么到它们的距离和一样。
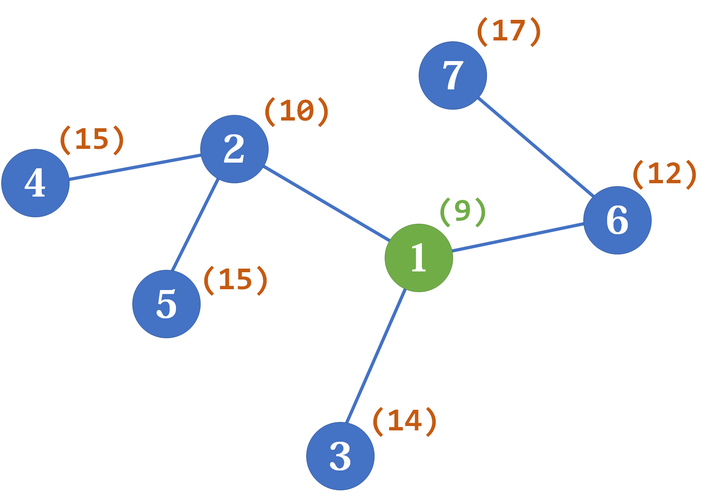
- 把两棵树通过一条边相连得到一棵新的树,那么新的树的重心在连接原来两棵树的重心的路径上。

- 在一棵树上添加或删除一个叶子,那么它的重心最多只移动一条边的距离。(往树上增加或减少一个叶子,如果原节点数是奇数,那么重心可能增加一个,原重心仍是重心;如果原节点数是偶数,重心可能减少一个,另一个重心仍是重心)
21-1-2 重心的查找
教父(poj 3107)
问题描述
城里有一个黑手党组织。把黑手党的人员关系用一棵树来描述,教父是树的根,每个节点是一个组织成员。为了保密,每人只和他的父节点和他的子节点联系。警察知道哪些人互相来往,但是不知他们的关系。警察想找出谁是教父。
警察假设教父是一个聪明人:教父懂得制衡手下的权力,所以他直属的几个小头目,每个人的属下的人数差不多。也就是说,删除根之后,剩下几棵互不连通的子树(连通块),其中最大的连通块应该尽可能小。请帮助警察找到哪些人可能是教父。
输入:第1行输入n,表示组织人数, 2 ≤ n ≤ 50000 2\leq n \leq 50000 2≤n≤50000 。组织成员的编号为1~n。下面n-1行中,每行输入两个整数,即有联系的两个人的编号。
输出:输出疑似教父的节点编号,从小到大输出。Input
6 1 2 2 3 2 5 3 4 3 6Output
2 3
- 分析
“删除根之后,剩下几棵互不连通的子树(连通块),其中最大的连通块应该尽可能小”,这句话说明了 教父 就是 这个关系树里的 重心
如何计算以 u节点 为根的子树的结点
u节点 DFS 直到“碰壁”后,将栈里的数据依次弹出,弹出一个结点数加1。
那么这样的话,可以对删除根之后,剩下几棵互不连通的子树(连通块) 进行单独的DFS,对整棵树逐一删除节点,重复上述步骤,就能得到每个结点的最大连同块。
如何优化?
上面提出的方案是 使用 暴力法 解决,其实无需如此,可以依照线段树的思维,对 同父节点的子节点 进行合并,得到父节点的子树的节点数,这样一次DFS就可以解决问题。
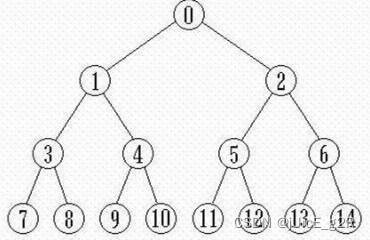
如上图,假如删除 结点1,得到3个连通块(含结点1的邻居:节点3、含结点1的邻居:节点0、含结点1的邻居:节点4)
对任意点做一次 DFS,特殊点,以 结点2为根节点 做DFS:
从2向0方向 一直DFS,直到遍历到节点10,停止遍历,栈开始弹出数据。,当弹出结点10时,记录 结点10 的度(即子树的结点数) D e g r e e [ 10 ] = 1 Degree[10]=1 Degree[10]=1,同理 D e g r e e [ 9 ] = 1 Degree[9]=1 Degree[9]=1;当弹出4时, D e g r e e [ 4 ] = D e g r e e [ 9 ] + D e g r e e [ 10 ] + 1 = 3 Degree[4]=Degree[9]+Degree[10]+1=3 Degree[4]=Degree[9]+Degree[10]+1=3,同理算出 D e g r e e [ 3 ] = D e g r e e [ 7 ] + D e g r e e [ 8 ] + 1 = 3 Degree[3]=Degree[7]+Degree[8]+1=3 Degree[3]=Degree[7]+Degree[8]+1=3;在弹出1时, D e g r e e [ 1 ] = D e g r e e [ 3 ] + D e g r e e [ 4 ] + 1 = 7 Degree[1]=Degree[3]+Degree[4]+1=7 Degree[1]=Degree[3]+Degree[4]+1=7;删除1后, D e g r e e [ 0 ] = n − D e g r e e [ 1 ] Degree[0]=n-Degree[1] Degree[0]=n−Degree[1]
存储:链式前向星
链式前向星较领接矩阵(二维数组)在空间上优化了很多
点击直通 链式前向星(图(树)的存储)
- 代码
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
vector<int> head(N,-1);
struct Edge{int to,next;Edge():to(-1), next(-1){} //初始化为无邻居节点
} edge[N<<1];
vector<int> Degree(N,1); //初始化每个节点的度(子树的结点数)为1
int edge_n=0; //记录边数
int GodFather_n=0; //记录可能得教父个数
int n; //人有n个,关系有n-1条
int MAX_Degree=1e9;
vector<int> ans(N,0);
void Add_Edge(int u, int v){edge[edge_n].to=v;edge[edge_n].next=head[u]; //记录 上一个邻居节点 的 存储编号head[u]=edge_n++; //当前 邻居节点 的 存储编号,以便下一个邻居节点的访问
}
void DFS(int u=1, int father=0){/*计算 cur结点 的 最大连通块的结点数*/int temp=0;for(int i=head[u]; ~i; i=edge[i].next){ //遍历cur节点的邻居节点[~i相当于i=-1]int v=edge[i].to; //v 是 u 的子节点if(v==father) continue;DFS(v,u); //DFS子树Degree[u]+=Degree[v]; //更新父节点的度temp=max(temp, Degree[v]); //记录cur结点的 最大子树 的 结点数}temp=max(temp, n-Degree[u]); //temp是cur最大连通块的节点数/*查找 结点数 最小的 最大连通块*/if(temp<MAX_Degree){ //满足条件的话,则temp是 疑似教父 的最大连通块的结点数MAX_Degree=temp; //更新 最小的 最大连通块GodFather_n=0; //找到新的最小,将它放在第一个ans[++GodFather_n]=u;}else if(temp==MAX_Degree)ans[++GodFather_n]=u;
}int main(int* argc, void* argv[]){cin>>n;for(int i=1; i<n;i++){int u,v; cin>> u >> v;Add_Edge(u,v); Add_Edge(v,u); //无向 记录 双向有向}DFS();sort(ans.data()+1, ans.data()+1+GodFather_n); //升序排列for(int i=1; i<=GodFather_n; i++)cout<<ans[i]<<" ";return 0;
}
相关文章:

【图论C++】树的重心——教父POJ 3107(链式前向星的使用)
》》》算法竞赛 /*** file * author jUicE_g2R(qq:3406291309)————彬(bin-必应)* 一个某双流一大学通信与信息专业大二在读 * * brief 一直在竞赛算法学习的路上* * copyright 2023.9* COPYRIGHT 原创技术笔记:转载…...

hhh百度地铁广告太搞笑了;24家国内大模型公司面经;LLM法律应用实践;AI+教育产品图谱与工作流 | ShowMeAI日报
👀日报&周刊合集 | 🎡生产力工具与行业应用大全 | 🧡 点赞关注评论拜托啦! 🔥 会玩儿!承包地铁专列,真人移动广告 | 百度世界大会预热 百度也是会玩儿!承包了北京地铁一号线的「…...

项目管理:项目经理一定要避开这四大误区
项目经理要保质保量按时达成项目目标,需要关注项目的方方面面,要具有很强的沟通协调能力和目标意识。但是项目经理也不免不了失误,管理中的这四大误区,你经历过几个? 误区一:做不该做的事 你是否遇到这种…...

爬虫为什么需要 HTTP 代理 IP?
前言 爬虫在互联网数据采集、分析和挖掘中扮演着至关重要的角色,但是对于目标网站而言,频繁的爬虫请求可能会对其服务器产生不小的负担,严重的情况甚至会导致网站崩溃或者访问受限。为了避免这种情况的发生,同时也为了保护客户端…...

leetcode刷题笔记/代码随想录笔记——移除字符串中多余空格
1. 使用erase()函数 void removeExtraSpaces(string& s) {for (int i s.size() - 1; i > 0; i--) {if (s[i] s[i - 1] && s[i] ) {s.erase(s.begin() i);}}// 删除字符串最后面的空格if (s.size() > 0 && s[s.size() - 1] ) {s.erase(s.begi…...
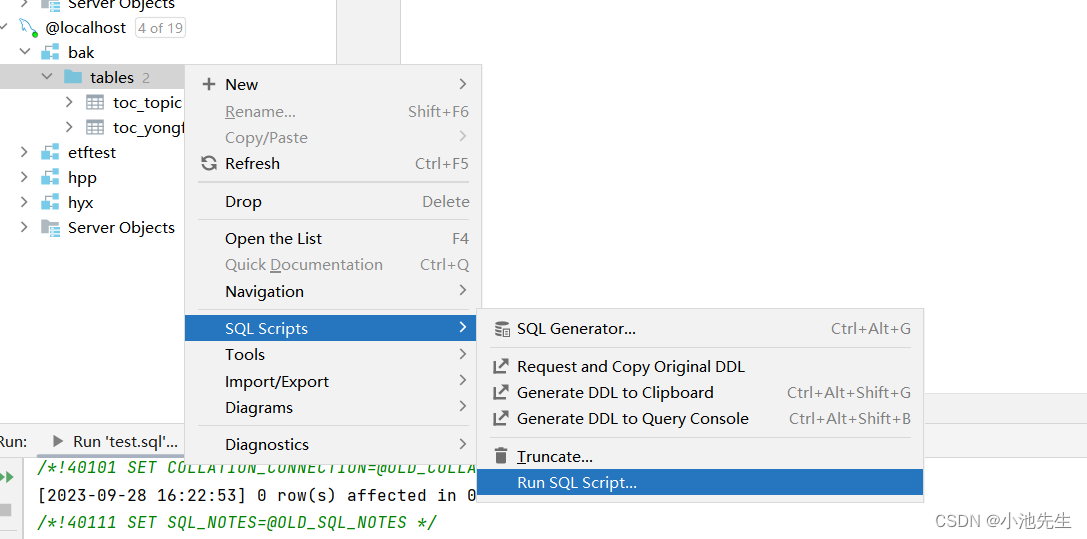
dataGrip导出导入的方式
导出:选中需要导出的表 导入:选中导出的sql文件...

LeetCode279. 完全平方数
279. 完全平方数 文章目录 [279. 完全平方数](https://leetcode.cn/problems/perfect-squares/)一、题目二、题解方法一:完全背包二维数组方法二:一维数组(空间复杂度更小的改进版本,最下面的两个版本不需要存储完全平方数) 一、题…...

【CMake】add_dependencies 命令
【CMake】add_dependencies 原文链接:https://blog.csdn.net/new9232/article/details/125831009 参考链接:https://blog.csdn.net/new9232/article/details/121374943 简介 add_dependencies(<target> [<target-dependency>]...)官方文档…...

go语言unsafe.Pointer与uintptr
以下内容来源go语言圣经 1、unsafe.Pointer,相当于c语言中的void *类型的指针,如果需要运算需要转成uintptr类型的指针 2. uintptr uintptr是一个无符号的整型,它可以保存一个指针地址。 它可以进行指针运算。 uintptr无法持有对象, GC不把…...

ddos打到高防cdn上会发生什么
ddos打到cdn上会发生什么?当DDoS攻击打到CDN上时,肯定会影响网站的可用性和用户体验。具体DDoS攻击打到CDN上时,会发生以下情况: CDN节点负载增加:DDoS攻击会导致大量的无效流量涌入CDN节点,从而使得节点负载增加。这…...

【单调栈】503. 下一个更大元素 II
503. 下一个更大元素 II 解题思路 参考496. 下一个更大元素 I 首先计算nums2的每一个元素的下一个比他大的元素,使用单调栈 将上面的结果和nums2中的每一个元素组成映射map 针对每一个Nums1的元素 查询map 记录map 的value 但是这个是循环的数组元素 class So…...

C++ decltype类型
文章目录 1. 工作原理2. decltype 变量3. decltype 表达式4. decltype 函数 1. 工作原理 随着程序越来越复杂,程序中用到的类型也越来越多,我们有时候不得不去翻阅大量上下文去寻找此数据的类型。 decltype就是一种类型说明符,它的出现…...

【题解】JZOJ3854 分组
JZOJ 3854 题意 有 n n n 个人,每个人有地位 r i r_i ri 和年龄 a i a_i ai,对于一个若干人组成的小组,定义其队长为地位最高的成员(若相等则取二者均可),其他成员的年龄与队长的差不能超过 k k …...

区块链实验室(26) - 区块链期刊Blockchain: Research and Applications
Elsevier出版物“Blockchain: Research and Applications”是浙江大学编审的期刊。该期刊自2020年创刊,并出版第1卷。每年出版4期,最新期是第4卷第3期(2023年9月)。 目前没有官方的IF,Elsevier的引用因子Citescore是6.4。 虽然是新刊…...

【学习笔记】[ARC153F] Tri-Colored Paths
假设三种颜色的边都存在,并且不存在这样的路径 首先观察到,对于一个简单环上的边,颜色一定相同 因此,考虑建立圆方树,问题转化为圆方树上的 D P DP DP问题。限制是对于方点所连接的边,必须涂上相同的颜色…...
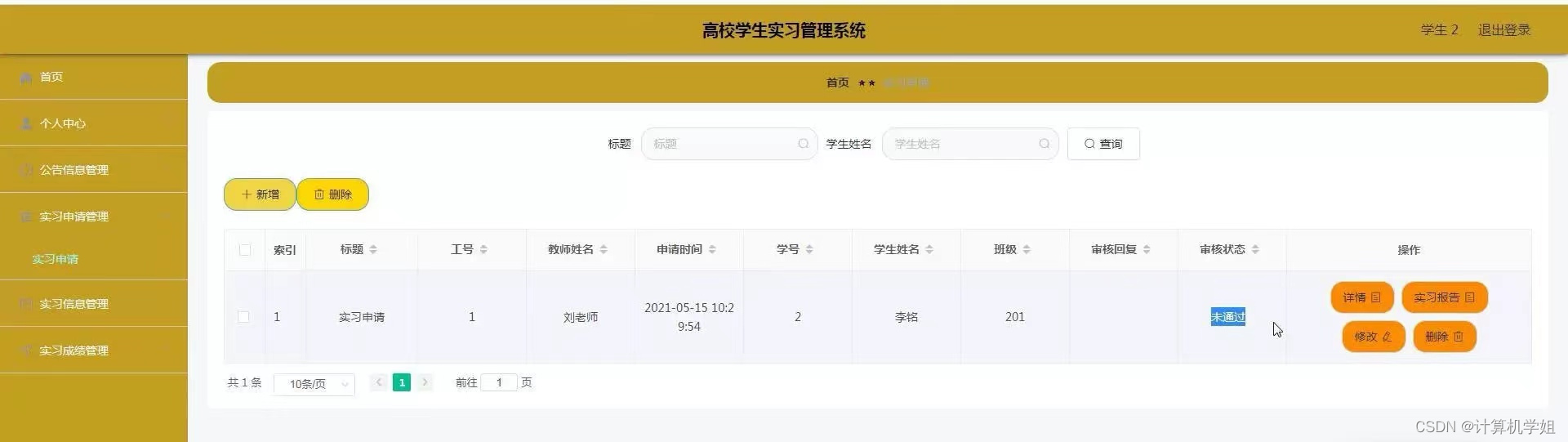
基于SSM的实习管理系统
基于SSM的实习管理系统、前后端分离 开发语言:Java数据库:MySQL技术:SpringSpringMVCMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 管理员界面 教师 学生 研究背景 基于SSM的实习管理系统是一个基于Spring、Spring…...
在Vue中通过ElementUI构建前端页面【登录,注册】,在IEDA构建后端实现前后端分离
一.ElementUI组件入门 1.对于ElementUI的理解 是一套基于 Vue.js 的开源UI组件库,提供了丰富的可复用组件,可以帮助开发者快速构建美观、易用的前端界面 2.Element UI 的特点和优势 多样化的组件:Element UI 提供了众多常用的基础组件&#…...

TX2 open ttyTHS2
TX2 open ttyTHS2 #冷风那个吹# 于 2019-04-01 14:10:43 发布 1749 收藏 6 分类专栏: 平时问题积累 TX2 版权 平时问题积累 同时被 2 个专栏收录 22 篇文章0 订阅 订阅专栏 TX2 30 篇文章8 订阅 订阅专栏 TX2上有5个串口,但是ttyTHS1是调试串口,ttyTHS3是蓝牙,ttyTHS…...

conan入门(二十八):解决conan 1.60.0下 arch64-linux-gnu交叉编译openssl/3.1.2报错问题
上一篇博客《conan入门(二十七):因profile [env]字段废弃导致的boost/1.81.0 在aarch64-linux-gnu下交叉编译失败》解决了conan 1.60.0交叉编译boost/1.80.1的问题后,我继续交叉编译openssl/3.1.2时又报错了 conan install openssl/3.1.2 -pr:h aarch64-linux-gnu.…...

Xcode 15 运行<iOS 14, 启动崩溃问题
如题. Xcode 15 启动 < iOS 14(没具体验证过, 我的问题设备是iOS 13.7)真机设备 出现启动崩溃 解决方案: Build Settings -> Other Linker Flags -> Add -> -ld64...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
