【题解】JZOJ3854 分组
JZOJ 3854
题意
有 n n n 个人,每个人有地位 r i r_i ri 和年龄 a i a_i ai,对于一个若干人组成的小组,定义其队长为地位最高的成员(若相等则取二者均可),其他成员的年龄与队长的差不能超过 k k k。 q q q 次询问,若将 x , y x,y x,y 安排在同一个小组,那么这个小组最多多少人。
题解
先预处理每个人当队长时小组最多有多少人。设这个值为 c n t i cnt_i cnti。
具体来说,按 r r r 排序,对于 i i i 需要求前面 i i i 个人有多少个人的年龄在 [ a i − k , a i + k ] [a_i-k,a_i+k] [ai−k,ai+k] 的区间内。用一个动态开点权值线段树即可。下标是年龄。
考虑对询问离线。不妨假设 r x ≤ r y r_x\le r_y rx≤ry,那么对于一个询问 i i i,能够包含 x i , y i x_i,y_i xi,yi 的队长的范围是 r ≥ r y i , max ( a x i , a y i ) − k ≤ a ≤ min ( a x i , a y i ) + k r\ge r_{y_i},\max (a_{x_i},a_{y_i}) - k\le a\le \min(a_{x_i},a_{y_i})+k r≥ryi,max(axi,ayi)−k≤a≤min(axi,ayi)+k。因为与 x , y x,y x,y 的年龄差要同时小于 k k k,所以选范围小的区间。
按 r y r_y ry 为关键值将询问从大到小排序。然后一个动态开点权值线段树,下标是年龄,叶子节点存储 c n t i cnt_i cnti。这样对于一个询问,只需要查找在 [ max ( a x i , a y i ) − k , min ( a x i , a y i ) + k ] [\max (a_{x_i},a_{y_i}) - k,\min(a_{x_i},a_{y_i})+k] [max(axi,ayi)−k,min(axi,ayi)+k] 区间内的最大值即可。
时间复杂度 O ( n log w ) O(n\log w) O(nlogw)。
实现
记得判 -1。注意输入的标号是排序前的标号,要处理一下。
#include <bits/stdc++.h>
using namespace std;
const int N = 100005, W = 1e9;
int n, K, Q, ans[N], vp[N], cnt[N];
int tr[N << 4], mx[N << 4], rt1 = 0, rt2 = 0, tot1 = 0, tot2 = 0, ls1[N << 4], rs1[N << 4], ls2[N << 4], rs2[N << 4];
struct mem {int r, ag, id;bool operator< (const mem &T) const { return r < T.r; }
} a[N];
struct Query {int x, y, id;bool operator< (const Query &T) const { return a[y].r > a[T.y].r; }
} q[N];
void upd1(int &rt, int x, int y, int pos, int val) {if (!rt) rt = ++tot1;if (x == y) { tr[rt] += val; return; }int mid = x + y >> 1;if (pos <= mid) upd1(ls1[rt], x, mid, pos, val);else upd1(rs1[rt], mid + 1, y, pos, val);tr[rt] = tr[ls1[rt]] + tr[rs1[rt]];
}
int qry1(int rt, int x, int y, int l, int r) {if (l > y || r < x || !rt) return 0;if (l <= x && y <= r) return tr[rt];int mid = x + y >> 1;return qry1(ls1[rt], x, mid, l, r) + qry1(rs1[rt], mid + 1, y, l, r);
}
void upd2(int &rt, int x, int y, int pos, int val) {if (!rt) rt = ++tot2;if (x == y) { mx[rt] = max(mx[rt], val); return; }int mid = x + y >> 1;if (pos <= mid) upd2(ls2[rt], x, mid, pos, val);else upd2(rs2[rt], mid + 1, y, pos, val);mx[rt] = max(mx[ls2[rt]], mx[rs2[rt]]);
}
int qry2(int rt, int x, int y, int l, int r) {if (l > y || r < x || !rt) return 0;if (l <= x && y <= r) return mx[rt];int mid = x + y >> 1;return max(qry2(ls2[rt], x, mid, l, r), qry2(rs2[rt], mid + 1, y, l, r));
}
int main() {scanf("%d%d", &n, &K);for (int i = 1; i <= n; i++) scanf("%d", &a[i].r), a[i].id = i;for (int i = 1; i <= n; i++) scanf("%d", &a[i].ag);sort(a + 1, a + n + 1);for (int i = 1; i <= n; i++) vp[a[i].id] = i;for (int i = 1; i <= n; ) {int j = i;while (a[j].r == a[j + 1].r) upd1(rt1, 1, W, a[j].ag, 1), j++;upd1(rt1, 1, W, a[j].ag, 1);for (; i <= j; i++) cnt[i] = qry1(rt1, 1, W, a[i].ag - K, a[i].ag + K);}scanf("%d", &Q);for (int i = 1; i <= Q; i++) {scanf("%d%d", &q[i].x, &q[i].y), q[i].x = vp[q[i].x], q[i].y = vp[q[i].y], q[i].id = i;if (q[i].x > q[i].y) swap(q[i].x, q[i].y);}sort(q + 1, q + Q + 1);int k = n;for (int i = 1; i <= Q; i++) {while (q[i].y <= k) upd2(rt2, 1, W, a[k].ag, cnt[k]), k--;ans[q[i].id] = qry2(rt2, 1, W, max(a[q[i].x].ag, a[q[i].y].ag) - K, min(a[q[i].x].ag, a[q[i].y].ag) + K);if (ans[q[i].id] < 2) ans[q[i].id] = -1;}for (int i = 1; i <= Q; i++) printf("%d\n", ans[i]);return 0;
}
相关文章:

【题解】JZOJ3854 分组
JZOJ 3854 题意 有 n n n 个人,每个人有地位 r i r_i ri 和年龄 a i a_i ai,对于一个若干人组成的小组,定义其队长为地位最高的成员(若相等则取二者均可),其他成员的年龄与队长的差不能超过 k k …...

区块链实验室(26) - 区块链期刊Blockchain: Research and Applications
Elsevier出版物“Blockchain: Research and Applications”是浙江大学编审的期刊。该期刊自2020年创刊,并出版第1卷。每年出版4期,最新期是第4卷第3期(2023年9月)。 目前没有官方的IF,Elsevier的引用因子Citescore是6.4。 虽然是新刊…...

【学习笔记】[ARC153F] Tri-Colored Paths
假设三种颜色的边都存在,并且不存在这样的路径 首先观察到,对于一个简单环上的边,颜色一定相同 因此,考虑建立圆方树,问题转化为圆方树上的 D P DP DP问题。限制是对于方点所连接的边,必须涂上相同的颜色…...
基于SSM的实习管理系统
基于SSM的实习管理系统、前后端分离 开发语言:Java数据库:MySQL技术:SpringSpringMVCMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 管理员界面 教师 学生 研究背景 基于SSM的实习管理系统是一个基于Spring、Spring…...
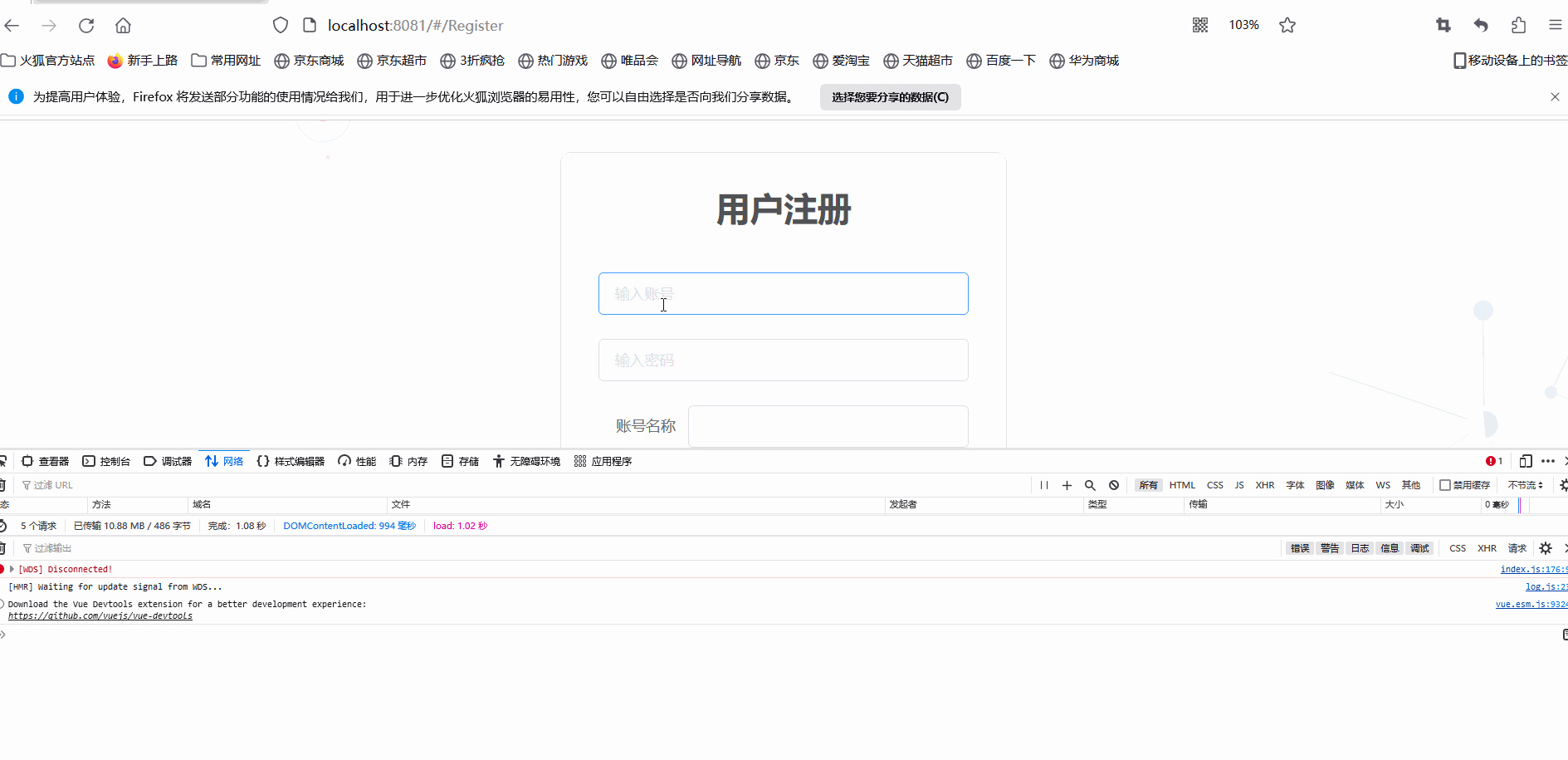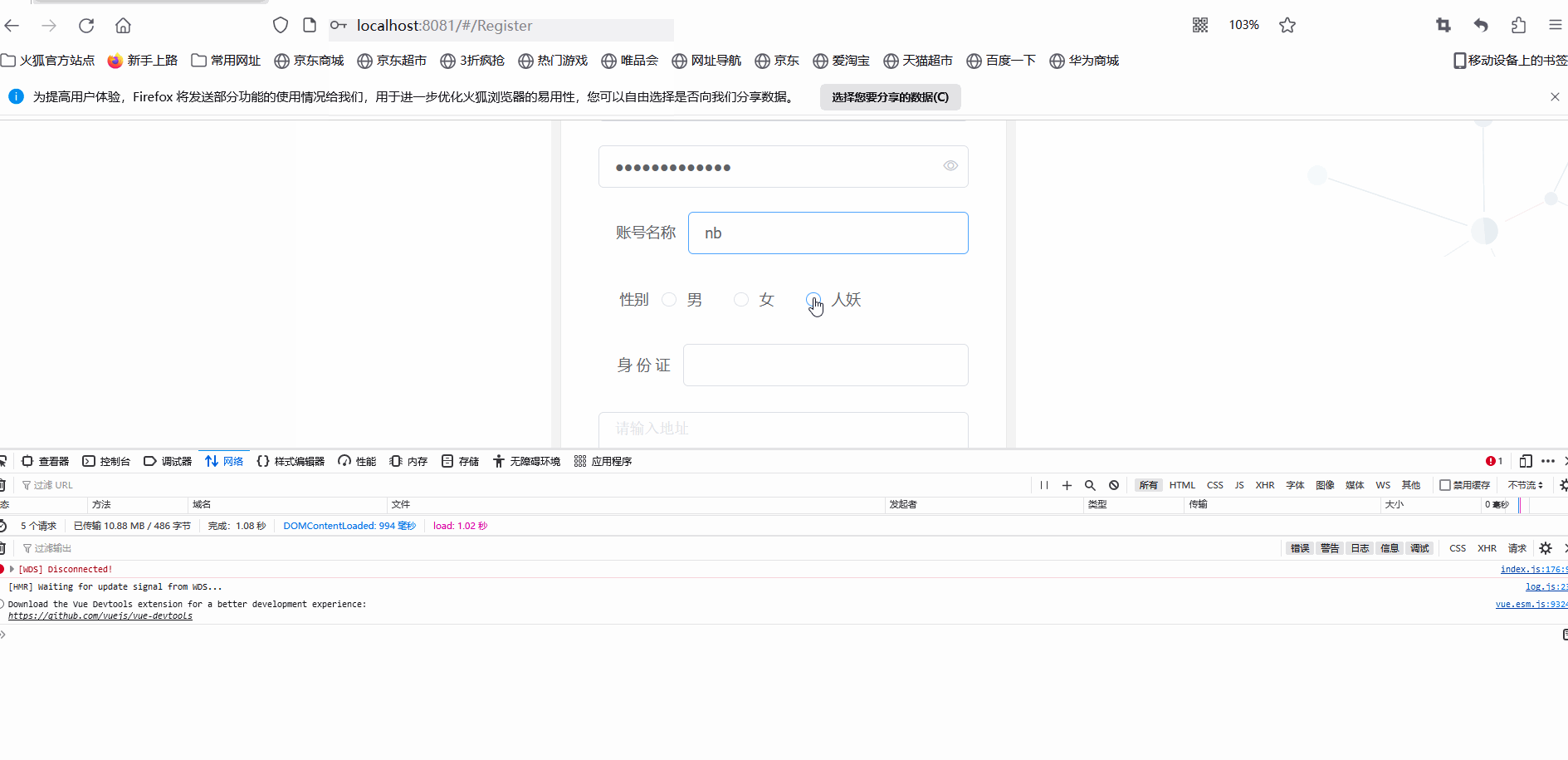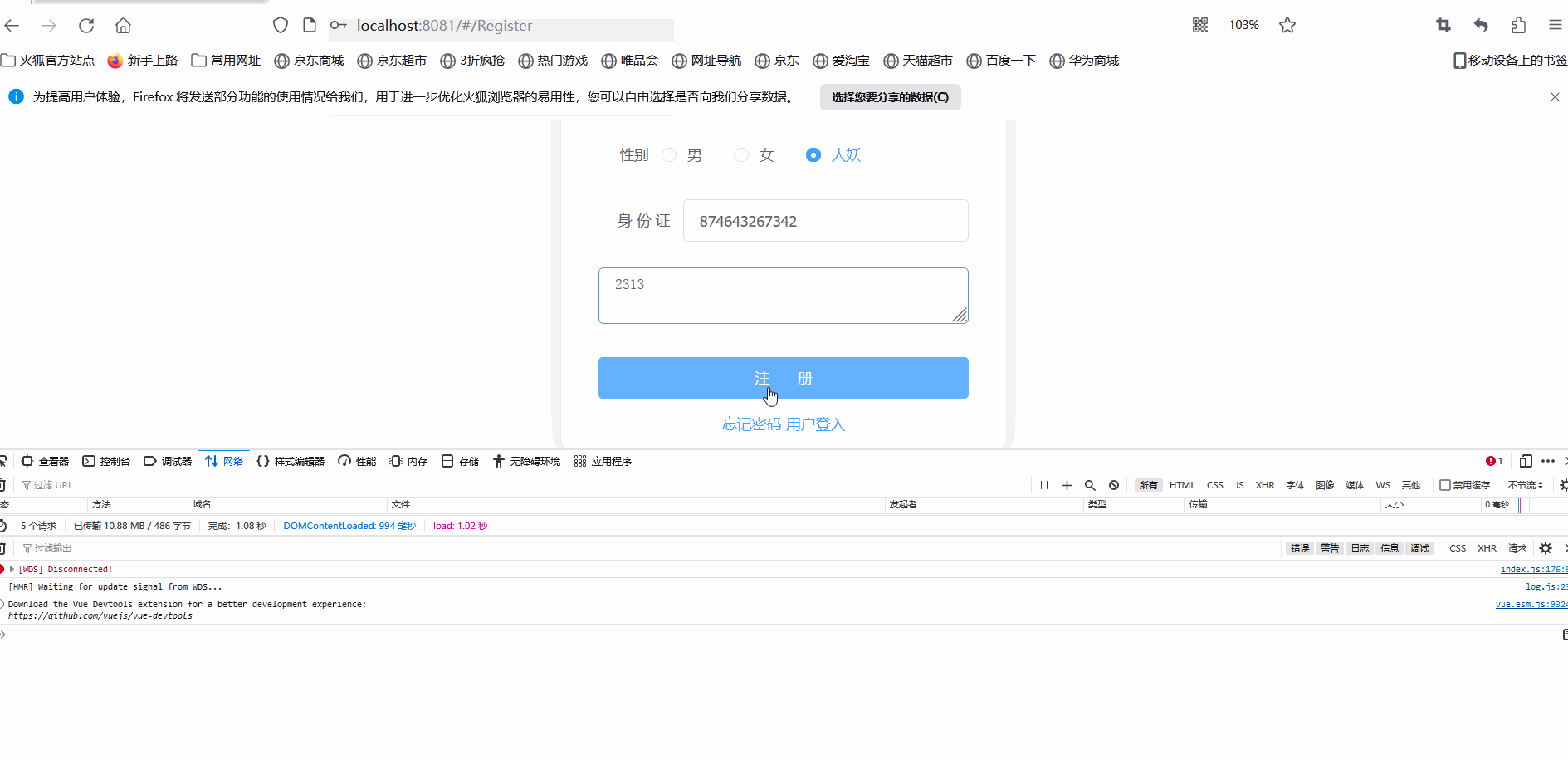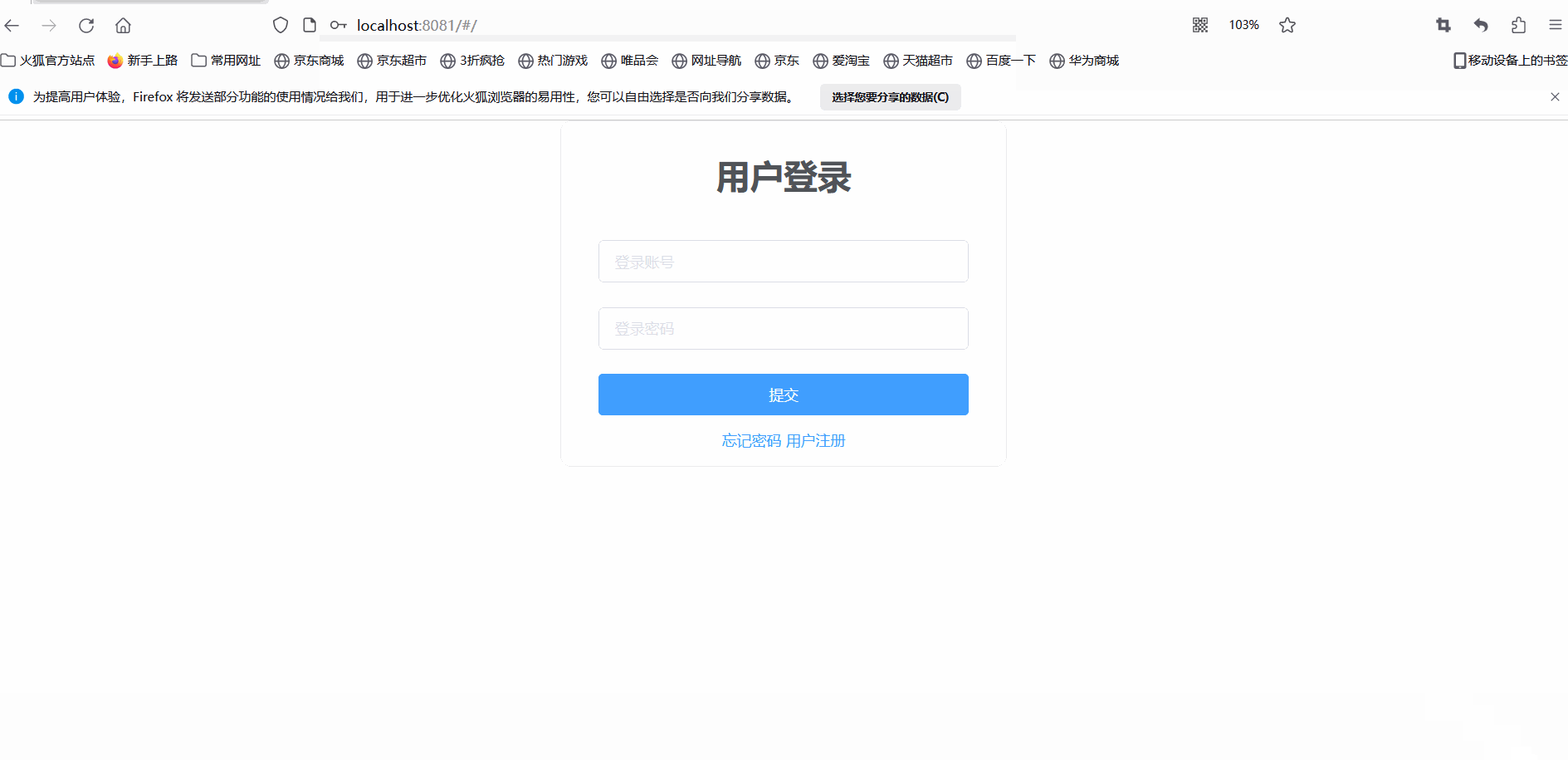
在Vue中通过ElementUI构建前端页面【登录,注册】,在IEDA构建后端实现前后端分离
一.ElementUI组件入门 1.对于ElementUI的理解 是一套基于 Vue.js 的开源UI组件库,提供了丰富的可复用组件,可以帮助开发者快速构建美观、易用的前端界面 2.Element UI 的特点和优势 多样化的组件:Element UI 提供了众多常用的基础组件&#…...

TX2 open ttyTHS2
TX2 open ttyTHS2 #冷风那个吹# 于 2019-04-01 14:10:43 发布 1749 收藏 6 分类专栏: 平时问题积累 TX2 版权 平时问题积累 同时被 2 个专栏收录 22 篇文章0 订阅 订阅专栏 TX2 30 篇文章8 订阅 订阅专栏 TX2上有5个串口,但是ttyTHS1是调试串口,ttyTHS3是蓝牙,ttyTHS…...

conan入门(二十八):解决conan 1.60.0下 arch64-linux-gnu交叉编译openssl/3.1.2报错问题
上一篇博客《conan入门(二十七):因profile [env]字段废弃导致的boost/1.81.0 在aarch64-linux-gnu下交叉编译失败》解决了conan 1.60.0交叉编译boost/1.80.1的问题后,我继续交叉编译openssl/3.1.2时又报错了 conan install openssl/3.1.2 -pr:h aarch64-linux-gnu.…...

Xcode 15 运行<iOS 14, 启动崩溃问题
如题. Xcode 15 启动 < iOS 14(没具体验证过, 我的问题设备是iOS 13.7)真机设备 出现启动崩溃 解决方案: Build Settings -> Other Linker Flags -> Add -> -ld64...
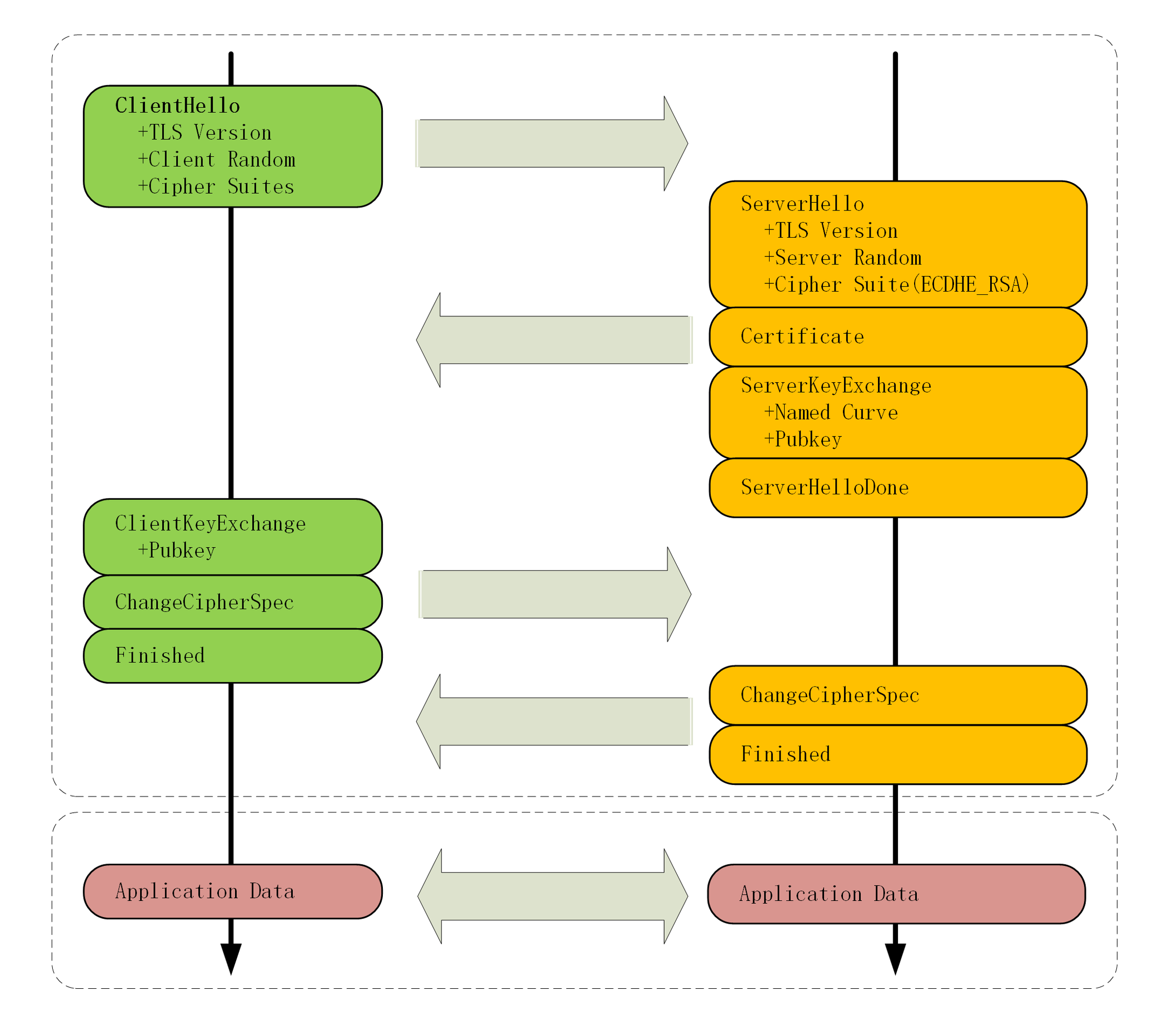
HTTPS协议概述
HTTPS(Hypertext Transfer Protocol over Secure Socket Layer,基于安全套接字层的超文本传输协议),是以安全为目标的HTTP通道,简单讲是HTTP的安全版。即HTTP下加入SSL层,HTTPS的安全基础是SSL,…...
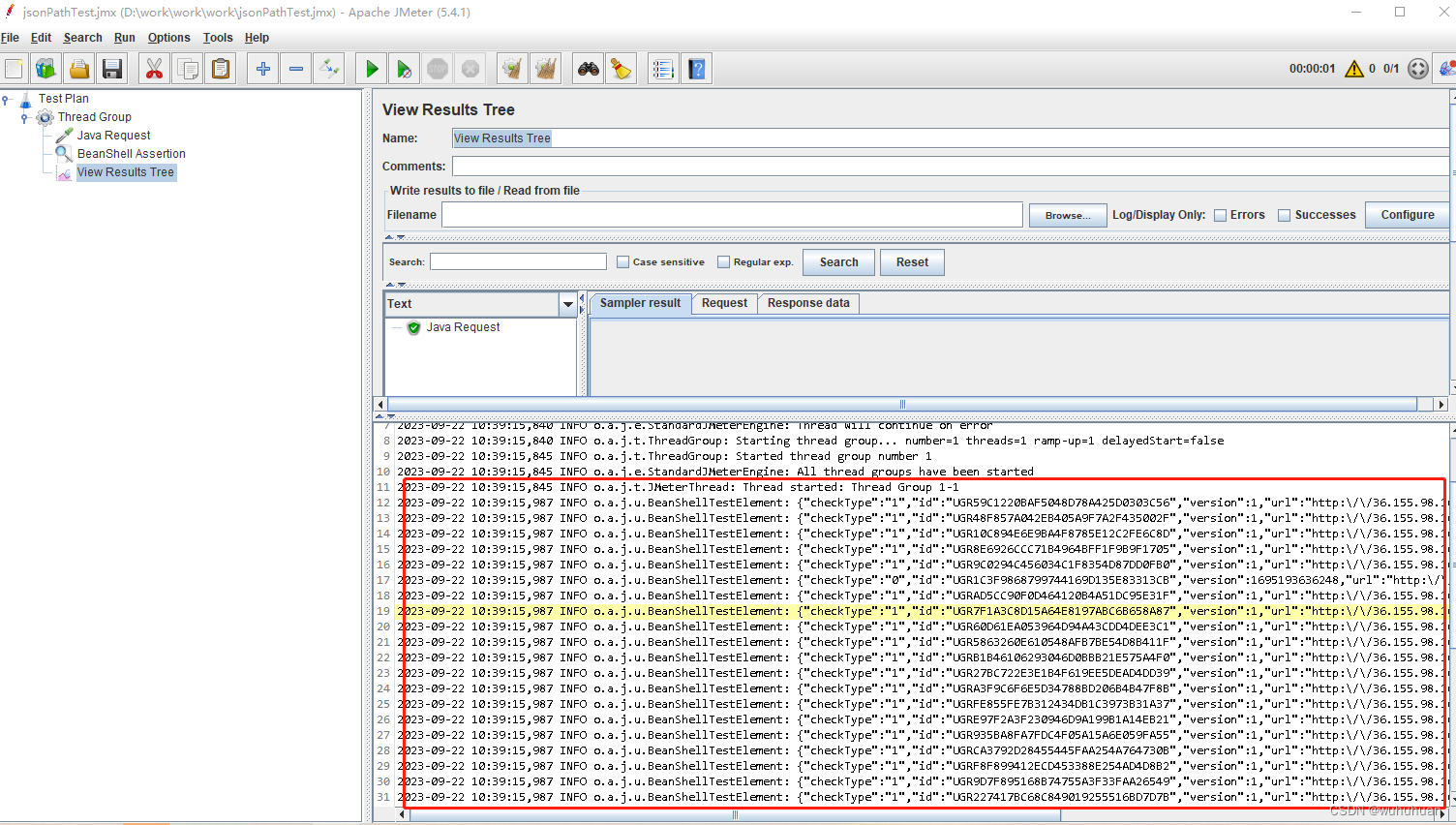
jmeterbeanshell调用jsonpath获取对应值
1.jmeter 新建线程组、Java Request、BeanShell Assertion、View Results Tree 2、在BeanShell Assertion中贴入代码: import org.apache.jmeter.extractor.json.jsonpath.JSONManager; import java.util.List; JSONManager js new JSONManager(); String jsonStr…...

C++中实现雪花算法来在秒级以及毫秒及时间内生成唯一id
1、雪花算法原理 雪花算法(Snowflake Algorithm)是一种用于生成唯一ID的算法,通常用于分布式系统中,以确保生成的ID在整个分布式系统中具有唯一性。它的名称来源于雪花的形状,因为生成的ID通常是64位的整数࿰…...
)
OPTEE Gprof(GNU profile)
安全之安全(security)博客目录导读 OPTEE调试技术汇总 目录 一、序言 二、Gprof使用 三、Gprof实现 1、Call graph information 2、PC distribution over time 一、序言 本文描述了如何使用gprof对TA进行概要分析。 配置选项CFG_TA_GPROF_SUPPORTy使OP-TEE能够从在用户模…...

MySQL 事务的操作指南(事务篇 二)
基本操作 事务的提交方式:自动提交(autocommit1)和手动提交(autocommit0) 查询和修改事务提交方式: -- 查看事务提交方式(标识表示这是个系统变量) select autocommit ;-- 修改事务提交方式为自动提交 …...

Oracle 查询 SQL 语句
目录 1. Oracle 查询 SQL 语句1.1. 性能查询常用 SQL1.1.1. 查询最慢的 SQL1.1.2. 列出使用频率最高的 5 个查询1.1.3. 消耗磁盘读取最多的 sql top51.1.4. 找出需要大量缓冲读取(逻辑读)操作的查询1.1.5. 查询每天执行慢的 SQL1.1.6. 从 V$SQLAREA 中查询最占用资源的查询1.1.…...

gin 基本使用
gin 初体验 import ("net/http""github.com/gin-gonic/gin" )func main() {r : gin.Default()r.GET("/ping", func(c *gin.Context) {c.JSON(http.StatusOK, gin.H{"message": "pong",})})r.Run() }gin 路由接受一个 type …...
8月最新修正版风车IM即时聊天通讯源码+搭建教程
8月最新修正版风车IM即时聊天通讯源码搭建教程。风车 IM没啥好说的很多人在找,IM的天花板了,知道的在找的都知道它的价值,开版好像就要29999,后端加密已解,可自己再加密,可反编译出后端项目源码,已增加启动后端需要google auth双重验证,pc端 web端 wap端 android端 ios端 都有 …...

NSDT孪生场景编辑器系统介绍
一、产品背景 数字孪生的建设流程涉及建模、美术、程序、仿真等多种人才的协同作业,人力要求高,实施成本高,建设周期长。如何让小型团队甚至一个人就可以完成数字孪生的开发,是数字孪生工具链要解决的重要问题。考虑到数字孪生复杂…...
3D WEB轻量化引擎HOOPS助力3D测量应用蓬勃发展:效率、精度显著提升
在3D开发工具领域,Tech Soft 3D打造的HOOPS SDK已经崭露头角,成为了全球领先的3D领域开发工具提供商。HOOPS SDK包括四种不同的3D软件开发工具,已成为行业的翘楚。 其中,HOOPS Exchange以其CAD数据转换的能力脱颖而出,…...

【Orange Pi】Orange Pi5 Plus 安装记录
官网:Orange Pi - Orangepi 主控芯片:Rockchip RK3588(8nm LP制程)NPU:内嵌的 NPU 支持INT4/INT8/INT16/FP16混合运算,算力高达 6Top支持的操作系统: Orangepi OS(Droid)Orangepi O…...

NLP 项目:维基百科文章爬虫和分类 - 语料库阅读器
塞巴斯蒂安 一、说明 自然语言处理是机器学习和人工智能的一个迷人领域。这篇博客文章启动了一个具体的 NLP 项目,涉及使用维基百科文章进行聚类、分类和知识提取。灵感和一般方法源自《Applied Text Analysis with Python》一书。 在接下来的文章中,我将…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...
