【运动控制】CNC三轴小线段路径规划

CNC三轴小线段路径规划

写在前面，本文是作为一个练手小项目的总结，方便以后自己查看，也欢迎大家批评指正。项目地址： GitHub

一、项目说明

参照论文《An optimal feedrate model and solution algorithm for a high-speed machine of small line blocks with look-ahead 》给出的方法给五轴机床做速度规划。输入原始的刀心数据(x,y,z,i,j,k)，对其进行速度规划和插补，获得插补后的数据(x,y,z,i,j,k)，然后通过运动学逆解转化成刀轴数据(x,y,z,b,c)。通过差分计算实际的速度和加速度与规划的速度进行对比，最后观察平滑滤波后的实际加速度。

二、具体实现

1、速度规划

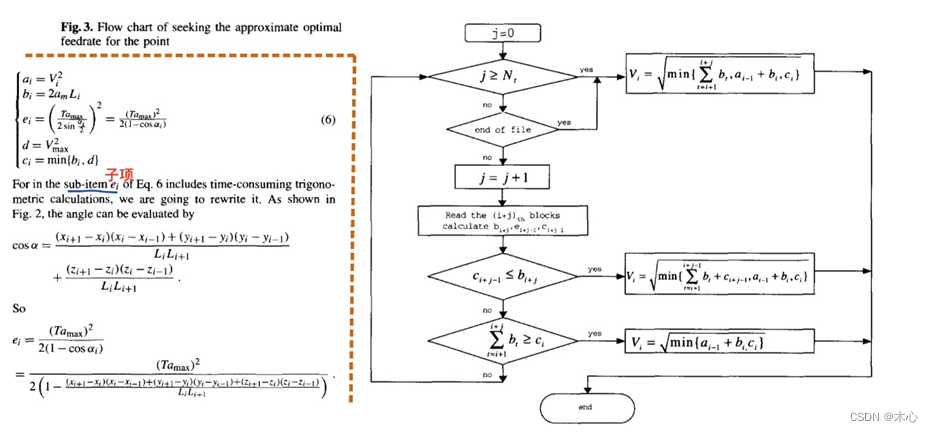
首先进行速度规划，按照如上的流程图（参考论文）对刀心的速度进行规划，计算得到每个刀心点对应的 ，具体的计算过程是先设定前瞻数，这里设定为4，然后通过判断上述循环条件，在

公式中选取对应的值作为当前的 ，具体的实现是代码中的speed_planning函数，函数的详细解释如下：

def speed_planning(traj_data, max_speed=MAX_SPEED, max_accel=MAX_ACCEL, corner_time=CORNER_TIME, period=PERIOD):""":@func:  参考《An optimal feedrate model and solution algorithm for a high-speed machine of small line blocks with look-ahead》给出的方法,进行速度规划:param traj_data: 路径信息shape(num,3) (x,y,z):param max_speed=0.05: 最大合成速率 m/s:param max_accel=0.5: 最大合成加速度 m/s^2:param corner_time=0.003: 拐弯时间 s:param period = 0.001: 插补周期 s:return:"""# 定义常量block_max = 4   # 最大前瞻数num = len(traj_data)# 开辟存储空间a = np.zeros([num])b = np.zeros([num])e = np.zeros([num])c = np.zeros([num])d = np.power(max_speed,2)Vs = np.zeros([num,1])# 节点差分dp = np.diff(traj_data, axis=0)# 初始化e[0] = db[0] = 0b[1] = 2*max_accel*np.sqrt(np.power(dp[0],2).sum())for i in range(1,num-1):  # Vs中第一个速度和最后一个速度都为0j = 0if j < block_max:if i+j <num:j=j+1b[i+j] = 2*max_accel*np.sqrt(np.power(dp,2).sum())e[i+j-1] = corner_time*max_accel*max_accel / (2*(1-(dp[i+j-2,0]*dp[i+j-1,0]+dp[i+j-2,1]*dp[i+j-1,1]+dp[i+j-2,2]*dp[i+j-1,2])/(np.sqrt(np.power(dp[i+j-2],2).sum())*np.sqrt(np.power(dp[i+j-1],2).sum()))))c[i+j-1] = np.min([e[i+j-1],d])if c[i+j-1] > b[i+j]:sum = 0for k in range(i+1,i+j):sum += b[k]if sum >= c[i]:Vs[i]=np.sqrt(np.min([Vs[i-1]*Vs[i-1]+b[i], e[i]]))elif c[i+j-1] <= b[i+j]:sum = 0for k in range(i+1,i+j):sum += b[k]Vs[i] = np.sqrt(np.min([sum+c[i+j-1], Vs[i-1]*Vs[i-1]+b[i], e[i]]))elif i+j >= num:sum = 0for k in range(i+1,i+j):sum += b[k]Vs[i] = np.sqrt(np.min([sum, Vs[i-1]*Vs[i-1]+b[i], e[i]]))elif j>= block_max:sum = 0for k in range(i+1,i+j):sum += b[k]Vs[i] = np.sqrt(np.min([sum, Vs[i-1]*Vs[i-1]+b[i], e[i]]))return Vs

2、小线段插补

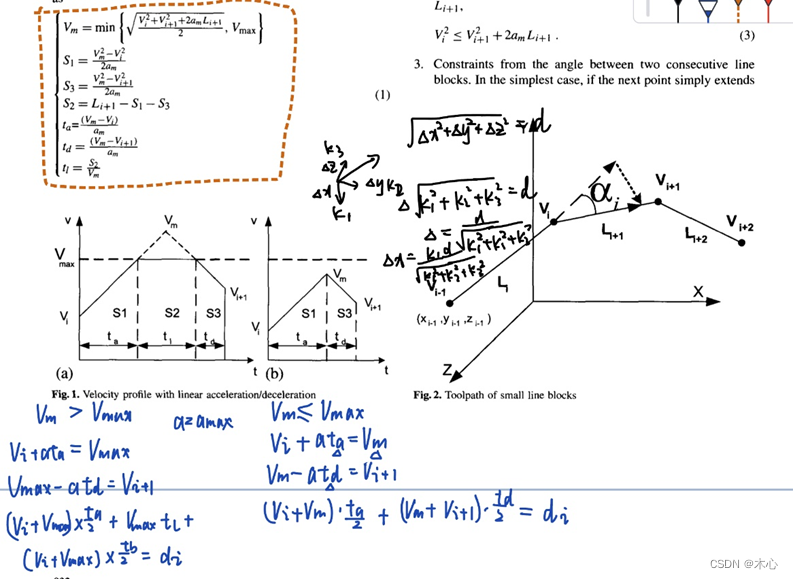
然后再按照上图的方法计算每一段插值时所需要的信息

具体实现函数是calc_lines_info

def calc_lines_info(path_data, plan_vels, max_speed=MAX_SPEED, max_accel=MAX_ACCEL):""":@func: 三轴小线段计算中间信息函数:param path_data:  初始路径信息 shape(n,6) (x,y,z,i,j,k):param plan_vels:  初始路径点的合成规划速度 shape(n,1):param max_speed = 0.05: 三轴最大合成速度  m/s:param max_accel = 0.5: 三轴最大合成加速度 m/s^2:return : """num = path_data.shape[0]# distances = np.zeros([num -1, 1])  #插值点间的距离shape(n-1, 3)dp = np.diff(path_data[:,0:3],axis=0)# 开辟存储空间vels_m = np.zeros([num -1])s1 = np.zeros([num -1])s2 = np.zeros([num -1])s3 = np.zeros([num -1])ta = np.zeros([num -1])td = np.zeros([num -1])tl = np.zeros([num -1])for i in range(num -1):# 计算距离# distances[i] = np.sqrt(np.power(path_data[i+1,0:3] - path_data[i,0:3],2).sum()) dis_i = np.sqrt(np.power(dp[i],2).sum())# 计算合成速度vi = plan_vels[i]vi_1 = plan_vels[i+1]# vels_m[i] = min(np.sqrt((np.power(vi,2) + np.power(vi_1,2) + 2*max_accel*distances[i])/2), max_speed)vels_m[i] = min(np.sqrt((np.power(vi,2) + np.power(vi_1,2) + 2*max_accel*dis_i)/2), max_speed)s1[i] = (np.power(vels_m[i],2) - np.power(vi,2))/2s3[i] = (np.power(vels_m[i],2) - np.power(vi_1,2))/2s2[i] = dis_i - s1[i] -s3[i]ta[i] = (vels_m[i] - vi) / max_acceltd[i] = (vels_m[i] - vi_1) / max_acceltl[i] = s2[i] / vels_m[i]return vels_m, ta, td, tl

然后我们进行单条线段的插补，函数实现是calc_axis_point

def calc_axis_point(start, end, Vi, Vi_1, Vm, timea, timed, timel, max_accel=MAX_ACCEL, period=PERIOD):""":@func:  计算一段的插补点:param start:  shape(6,):param end: shape(6,):param Vm: 该段的最大速度:param Vi: 起始速度:param Vi_1: 终点速度:param timea: 加速时间:param timed: 匀速时间:param timel: 减速时间:return: 返回给定两点之间的插补点,shape(n,6)"""dist = np.sqrt(np.power(end[0:3]-start[0:3],2).sum())# 计算三轴x,y,z分别所占的比例k1 = (end[0:3]-start[0:3])[0] / np.sqrt(np.power(end[0:3]-start[0:3],2).sum())k2 = (end[0:3]-start[0:3])[1] / np.sqrt(np.power(end[0:3]-start[0:3],2).sum())k3 = (end[0:3]-start[0:3])[2] / np.sqrt(np.power(end[0:3]-start[0:3],2).sum())# 计算法向量的比例delta = (end[3:]-start[3:]) / (timea+timed+timel)# 插值周期数t_count = 1V1 = Vi         #起始点速度V2 = Vi_1       #终点速度# 开辟存储空间line_points = np.zeros([1,6])dis = 0while(t_count*period <= timea+timed+timel and dis<=dist):# 计算加速时间内的插值点if t_count*period <= timea:dis += V1*period + 0.5*max_accel*period*periodV1 += max_accel*periodif V1 > Vm:V1 = Vmt_count += 1delta_vec = delta * t_count * perioddelta_xyz = np.concatenate([k1*dis, k2*dis, k3*dis], axis=0)dp = np.concatenate([delta_xyz, delta_vec], axis=0)p = start + dpline_points = np.vstack([line_points, p])# 计算匀速时间内的插值点elif timea < t_count*period <= timea+timel and timel!=0:dis += V1 * periodt_count += 1delta_vec = delta * t_count * perioddelta_xyz = np.concatenate([k1*dis, k2*dis, k3*dis], axis=0)dp = np.concatenate([delta_xyz, delta_vec], axis=0)p = start + dpline_points = np.vstack([line_points, p])# 计算减速时间内的插值点elif timea+timel < t_count*period <= timea+timel+timed:dis += V1*period - 0.5*max_accel*period*periodV1 = V1 - max_accel*periodif V1 < V2:V1 = V2t_count += 1delta_vec = delta * t_count * perioddelta_xyz = np.concatenate([k1*dis, k2*dis, k3*dis], axis=0)dp = np.concatenate([delta_xyz, delta_vec], axis=0)p = start + dpline_points = np.vstack([line_points, p])return line_points[1:]

再进行多条线段插补，函数实现是calc_axis_points

def calc_axis_points(path_data, plan_vels, max_speed=MAX_SPEED, max_accel=MAX_ACCEL, corner_time=CORNER_TIME, period=PERIOD):""":@func:  计算所有的插补点:param path_data:  shape(num,6):param plan_vels: shape(num,):param max_speed = 0.05: 三轴最大合成速度  m/s:param max_accel = 0.5: 三轴最大合成加速度 m/s^2:param corner_time = 0.003: 拐弯时间 s:param period = 0.001: 固定插补周期 s:return: 所有的插补点,shape(n,6)"""vels_m, ta, td, tl = calc_lines_info(path_data, plan_vels, max_speed, max_accel)# 开辟存储空间axis_points = np.zeros([1,6])num = len(path_data) - 1for i in range(num):line_points = calc_axis_point(path_data[i], path_data[i+1], plan_vels[i], plan_vels[i+1], vels_m[i], ta[i], td[i], tl[i], max_accel, period)axis_points = np.vstack([axis_points, line_points])return axis_points[1:]

3、运动学逆解刀轴插补点

然后使用运动学逆解，求出刀轴的坐标，函数实现是inv_kinema

def inv_kinema(path_data):""":@func: 求解逆运动学:param path_data: 刀心路径点信息 shape(num,6) (x,y,z,i,j,k):return :  求解的刀轴信息 shape(num,5) (x,y,z,b,c)"""#加载数据points = read_path_data(DATA_PATH)curve_points = points[:,0:3]    # 路径normal_vectors = points[:,3:]  # 法向量# 旋转轴初始方向wc = sympy.Matrix([[0], [0], [1]])wb = sympy.Matrix([[0], [0.5 * sympy.sqrt(2)], [0.5 * sympy.sqrt(2)]])theta_b, theta_c ,x,y,z= sympy.symbols('theta_b theta_c x y z')# 对C旋转cRodrigues = Rodrigues(wc, theta_c)# 对B旋转bRodrigues = Rodrigues(wb, theta_b)# print(bRodrigues)zero=np.zeros((3,1))# 生成旋转矩阵ec=np.append(cRodrigues,zero,axis=1)e_bu=np.array([0,0,0,1]).reshape(1,4)e_c=np.append(ec,e_bu,axis=0).reshape(4,4)eb=np.append(bRodrigues,zero,axis=1)e_b=np.append(eb,e_bu,axis=0).reshape(4,4)# print(eb,e_b)e_x=np.array([1,0,0,x,0,1,0,0,0,0,1,0,0,0,0,1]).reshape(4,4)e_y=np.array([1,0,0,0,0,1,0,y,0,0,1,0,0,0,0,1]).reshape(4,4)e_z=np.array([1,0,0,0,0,1,0,0,0,0,1,z,0,0,0,1]).reshape(4,4)# 初始位型mt0 = np.array([1,0,0,10,0,1,0,20,0,0,1,100,0,0,0,1]).reshape(4,4)gmw=np.eye(4)gmt1=np.dot(e_x,e_y)gmt2= np.dot(gmt1,e_z)gmt3=np.dot(e_c,e_b)gmt4=np.dot(gmt3,mt0)gmt=np.dot(gmt2,gmt4)# 转移矩阵gm=np.dot(gmw,gmt)# 带入解析式，求解bx = normal_vectors[:,0]/np.linalg.norm(normal_vectors[:,0])#归一化by = normal_vectors[:,1]/np.linalg.norm(normal_vectors[:,1])bz = normal_vectors[:,2]/np.linalg.norm(normal_vectors[:,2])x = curve_points[:,0]y = curve_points[:,1]z = curve_points[:,2] print(2*bz-1)theta_b = np.arccos(2*bz-1)theta_c = np.arcsin(((bz-1)*bx+np.sqrt(2)*np.sqrt(bz-bz**2)*by)/(1-bz**2))# 存数据myfile = open("path_interpolation_xyzbc.txt", "w")myfile.write('x   y   z   b   c\n')for i in range(0, normal_vectors.__len__()):myfile.write('{:>6.3f} '.format(x[i]))myfile.write('{:>6.3f} '.format(y[i]))myfile.write('{:>6.3f} '.format(z[i]))myfile.write('{:>6.3f} '.format(theta_b[i]))myfile.write('{:>6.3f}\n'.format(theta_c[i]))myfile.close()

4、差分处理得到实际的速度和加速度

接着用速度差分查看实际的速度，函数实现是diff_vel_accel

def diff_vel_accel(axis_points, period=PERIOD):""":@func:  通过五轴插补点计算实际速度和实际加速度:param axis_points:  实际插补点:param period: 插补周期:return: 实际速度, 实际加速度"""delta_d = np.diff(axis_points[:,0:3], axis=0)dv = delta_d / periodreal_vels = np.sqrt(np.power(dv,2).sum(axis=1))delta_v = np.diff(dv, axis=0)da = delta_v / periodreal_accels = np.sqrt(np.power(da,2).sum(axis=1))# print(real_vels[0:5])# print(real_accels[0:5])# 将实际速度写入到文件real_velocities.txt中write2file('real_velocities.txt', real_vels, string = "real velocities")# 将实际加速度写入到文件real_accelerations.txt中write2file('real_accelerations.txt', real_accels, string="real accelerations")return real_vels, real_accels

5、加速度滑动平均

最后对实际的加速度进行滑动平均，与设定值进行比较，函数实现是sliding_average

def sliding_average(data, window_size):""":@func: 实现滑动平均滤波:param data: 滑动滤波的数据:param window_size:  滑动窗口大小"""filtered_data = []for i in range(len(data)):if i < window_size:filtered_data.append(sum(data[:i+1]) / (i+1))else:filtered_data.append(sum(data[i-window_size+1:i+1]) / window_size)write2file("filtered_accelerations.txt", filtered_data, string = "filtered accelerations")return filtered_data

6、实现的效果如图所示

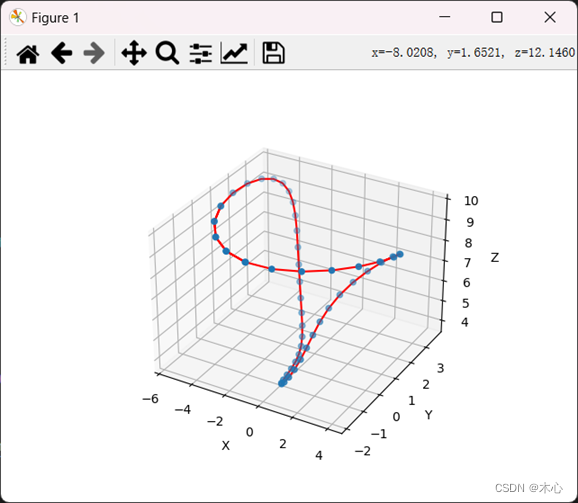
其中，蓝色的点是原始路径点，红色的线是由插补点绘制的小线段轨迹。

三、Reference

1、《An optimal feedrate model and solution algorithm for a high-speed machine of small line blocks with look-ahead 》