自定义hooks之useLastState、useSafeState
自定义hooks之useLastState、useSafeState
useLastState
在某些情况下,可能需要知道状态的历史值,例如,希望在状态变化时执行某些操作,但又需要访问上一个状态的值,以便进行比较或其他操作。自定义 React Hook 可以帮助我们封装和重用组件逻辑。这里介绍的useLastState Hook 可以用于跟踪组件状态的历史变化,可以获取上一个状态的值。
以下是一个实现 useLastState Hook 的示例:
import { useState, useEffect } from 'react';function useLastState(initialState) {const [state, setState] = useState(initialState);const [lastState, setLastState] = useState(initialState);// 使用 useEffect 来监听 state 的变化,并在 state 变化时更新 lastStateuseEffect(() => {setLastState(state);}, [state]);// 返回一个包含当前 state 和上一个 state 的数组return [state, lastState, setState];
}export default useLastState;
上面的 useLastState Hook 接受一个初始状态值作为参数,并返回一个包含当前状态、上一个状态以及一个更新状态的函数的数组。
使用这个 Hook 的示例:
import React from 'react';
import useLastState from './useLastState';function MyComponent() {const [count, lastCount, setCount] = useLastState(0);const handleIncrement = () => {setCount(count + 1);};return (<div><p>Current Count: {count}</p><p>Last Count: {lastCount}</p><button onClick={handleIncrement}>Increment</button></div>);
}export default MyComponent;
在上述示例中,MyComponent 使用 useLastState Hook 来跟踪 count 的状态,并在界面上显示当前计数和上一个计数的值。当点击 “Increment” 按钮时,count 会增加,同时 lastCount 会更新为前一个状态的值。
使用场景
-
图表组件:当需要在图表组件中跟踪数据的历史变化,以便在数据变化时执行比较或动画效果时,可以使用
useLastState。例如,在绘制图表时,可以比较当前数据和上一次数据,以确定何时触发图表的动画效果。 -
计数器组件:在计数器组件中,可能希望显示当前计数值以及上一次计数值,以便用户可以看到计数的变化情况。
-
表格排序:当用户点击表格列标题进行排序时,可以使用
useLastState来跟踪上一次的排序状态,以确定排序的方向(升序或降序),并在表格中显示排序箭头。
useSafeState
useSafeState 是一个自定义 React Hook,用于确保在组件卸载后不再更新组件状态。这是为了解决异步操作(如数据请求或定时器)可能在组件卸载后仍然触发状态更新的常见问题,有助于处理异步操作和组件生命周期的常见问题的方式,确保组件卸载后不再更新状态,提高了代码的稳定性。
以下是一个实现 useSafeState Hook 的示例:
import { useState, useEffect, useCallback } from 'react';function useSafeState(initialState) {const [state, setState] = useState(initialState);const isMounted = useRef(true);useEffect(() => {isMounted.current = true;return () => {isMounted.current = false;};}, []);const safeSetState = useCallback((newState) => {if (isMounted.current) {setState(newState);}},[setState]);return [state, safeSetState];
}export default useSafeState;
使用这个 Hook 的示例:
import React, { useEffect } from 'react';
import useSafeState from './useSafeState';function MyComponent() {const [count, setCount] = useSafeState(0);useEffect(() => {const timer = setInterval(() => {setCount((prevCount) => prevCount + 1);}, 1000);return () => {clearInterval(timer); // 确保在组件卸载时清除定时器};}, [setCount]);return (<div><p>Count: {count}</p></div>);
}export default MyComponent;
在上述示例中,useSafeState Hook 用于跟踪计数的状态,同时在组件卸载时清除定时器。这确保了即使在组件卸载后,定时器仍然触发状态更新的情况下,不会引发 React 的警告或错误。
使用场景
-
数据请求:在进行数据请求时,如果请求返回数据需要更新组件的状态,但在请求期间用户可能离开当前页面或组件已卸载,为了避免在组件卸载后更新状态而导致错误,可以使用
useSafeState。 -
定时器:在使用定时器执行周期性任务时,如果组件在定时器触发时已经卸载,为了防止更新已卸载组件的状态,可以使用
useSafeState来确保定时器回调函数不会触发状态更新。 -
事件监听器:在添加 DOM 事件监听器时,如果组件卸载时没有正确移除事件监听器,可能会导致内存泄漏或不稳定的行为。
useSafeState可以用于确保在组件卸载时不再触发事件监听器的回调函数。
本文使用 文章同步助手 同步
相关文章:

自定义hooks之useLastState、useSafeState
自定义hooks之useLastState、useSafeState useLastState 在某些情况下,可能需要知道状态的历史值,例如,希望在状态变化时执行某些操作,但又需要访问上一个状态的值,以便进行比较或其他操作。自定义 React Hook 可以帮…...

前端判断: []+[], []+{}, {}+[], {}+{}
本质: 二元操作符规则 一般判断规则: 如果操作数是对象,则对象会转换为原始值如果其中一个操作数是字符串的话,另一个操作数也会转换成字符串,进行字符串拼接否则,两个操作数都将转换成数字或NaN,进行加法操作 转为原始数据类型的值的方法: Symbol.ToPrimitiveObject.protot…...
)
el-input-number/el-input 实现实时输入数字转换千分位(失焦时展示千分位)
el-input-number/el-input 实现实时输入数字转换千分位(失焦时展示千分位) 我把封装指令的代码放在了main.js,代码如下 // 金额展示千分位 Vue.directive("thousands", {inserted: function(el, binding) {// debugger// 获取input节点if (el.tagName.toLocaleUppe…...

一篇博客学会系列(2)—— C语言中的自定义类型 :结构体、位段、枚举、联合体
目录 前言 1、结构体 1.1、结构体类型的声明 1.2、特殊的结构体类型声明 1.3、结构体的自引用 1.4、结构体的定义和初始化 1.5、结构体成员变量的调用 1.6、结构体内存对齐 1.6.1、offsetof 1.6.2、结构体大小的计算 1.6.3、为什么存在内存对齐? 1.7、…...
KongA 任意用户登录漏洞分析
KongA 简介 KongA 介绍 KongA 是 Kong 的一个 GUI 工具。GitHub 地址是 https://github.com/pantsel/konga 。 KongA 概述 KongA 带来的一个最大的便利就是可以很好地通过UI观察到现在 Kong 的所有的配置,并且可以对于管理 Kong 节点 漏洞成因 未设置TOKEN_SECRE…...
吉力宝:智能科技鞋品牌步力宝引领传统产业创新思维
在现代经济环境下,市场经济下产品的竞争非常的激烈,如果没有营销,产品很可能不被大众认可,酒香也怕巷子深,许多传统产业不得不面临前所未有的挑战。而为了冲出这个“巷子”,许多企业需要采用创新思维&#…...
)
【IPC 通信】信号处理接口 Signal API(1)
收发信号思想是 Linux 程序设计特性之一,一个信号可以认为是一种软中断,通过用来向进程通知异步事件。 本文讲述的 信号处理内容源自 Linux man。本文主要对各 API 进行详细介绍,从而更好的理解信号编程。 信号概述 遵循 POSIX.1,…...
使用GDIView排查GDI对象泄漏导致的程序UI界面绘制异常问题
目录 1、问题说明 2、初步分析 3、查看任务管理器,并使用GDIView工具分析 4、GDIView可能对Win10兼容性不好,显示的GDI对象个数不太准确 5、采用历史版本比对法,确定初次出现问题的时间点,并查看前一天的代码修改记录 6、将…...

蓝桥等考Python组别一级001
第一部分:选择题 1、Python L1 (15分) 下面哪个不是Python的编程环境?( ) Python在线编程IDLEPyCharmScratch正确答案:D 2、Python L1(15分) 世界上第一台通用电子计算机ENIAC是在( )诞生的。 美国英国日本德国正确答案:A 3、Python L1(20分) 关于P…...

Unity之Hololens2开发 如何接入的MRTK OpenXR Plugin
一.前言 什么是Hololens? Hololens是由微软开发的一款混合现实头戴式设备,它将虚拟内容与现实世界相结合,为用户提供了沉浸式的AR体验。Hololens通过内置的传感器和摄像头,能够感知用户的环境,并在用户的视野中显示虚拟对象。这使得用户可以与虚拟内容进行互动,将数字信…...
Ubuntu系统Linux内核安装和使用
安装: 检查树莓派Linux版本,我的是6.1 uname -r 内核下载链接: Raspberry Pi GitHub 找对应版本下载 导入之后,解压安装即可 unzip linux-rpi-6.1.y.zip 其他内容 treee 指令安装 sudo apt-get install tree 使用这…...
”)
数学术语之源——群同态的“核(kernel)”
1. “kernel”这个术语在群论中的起源 Ivar Fredholm 在 1903 年的第27期Acta Math 数学学报发表的一篇关于“积分方程(INTEGRAL EQUATIONS)”的著名论文(“关于一类函数方程(Sur une classe des quations fonctionnelles)”)中使用了法语“noyau(核)”(365-390页)。 David …...
defcon-quals 2023 crackme.tscript.dso wp
将dso文件放到data/ExampleModule目录下,编辑ExampleModule.tscript文件 function ExampleModule::onCreate(%this) { trace(true); exec("./crackme"); __main("aaaaaaaa"); quit(); } 然后点击主目录下的Torque3D-debug.bat就可以在生成的c…...

前端开发 vs. 后端开发:编程之路的选择
文章目录 前端开发:用户界面的创造者1. HTML/CSS/JavaScript:2. 用户体验设计:3. 响应式设计:4. 前端框架: 后端开发:数据和逻辑的构建者1. 服务器端编程:2. 数据库:3. 安全性&#…...

算法练习4——删除有序数组中的重复项 II
LeetCode 80 删除有序数组中的重复项 II 给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。 不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 …...
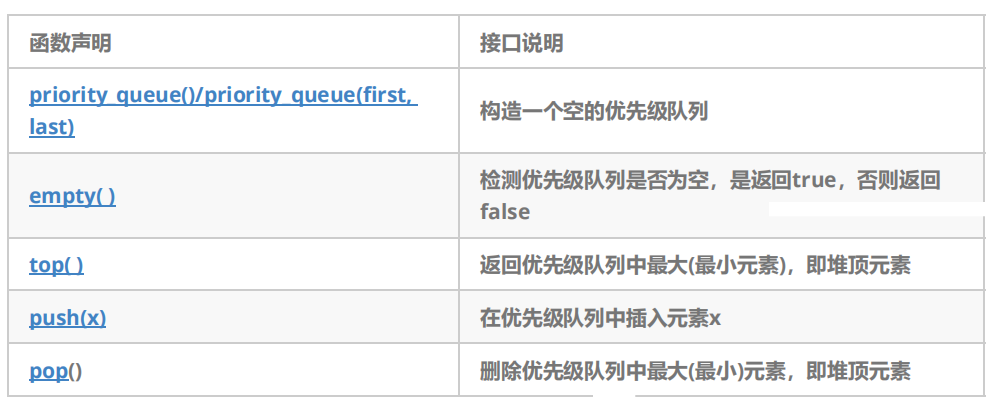
【C++进阶(六)】STL大法--栈和队列深度剖析优先级队列适配器原理
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:C从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习C 🔝🔝 栈和队列 1. 前言2. 栈和队列的接口函数熟悉3. …...

linux opensuse使用mtk烧录工具flashtool
环境 linux发行版:opensuse leap 15.5 工具:SP_Flash_Tool_Selector_exe_Linux_v1.2316.00.100.rar 或其他版本 目标:mtk设备 下载链接 https://download.csdn.net/download/zmlovelx/88382784 或网络搜索。 使用 opensuse可直接解压后使…...
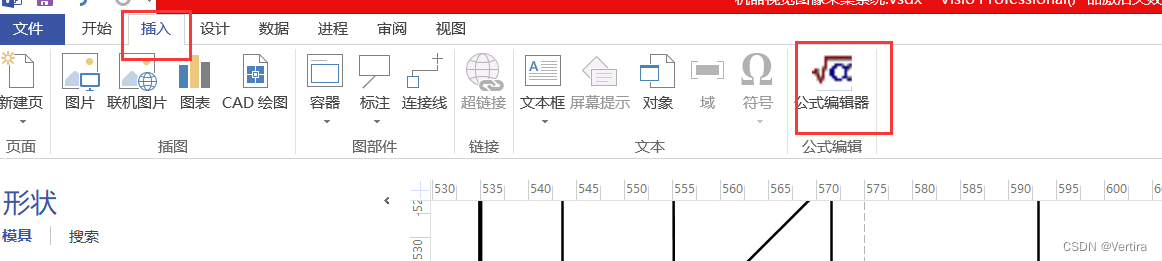
Visio如何对文本打下标、上标,以及插入公式编辑器等问题(已解决)
解决这个问题的本质问题,就是在Visio中插入公式编辑器(这不是visio的常用命令,需要添加)。 打开Visio--》文件--选项 点击选项,弹出对话框。在自定义功能区中,点击 常用命令,在下拉选项中&#…...
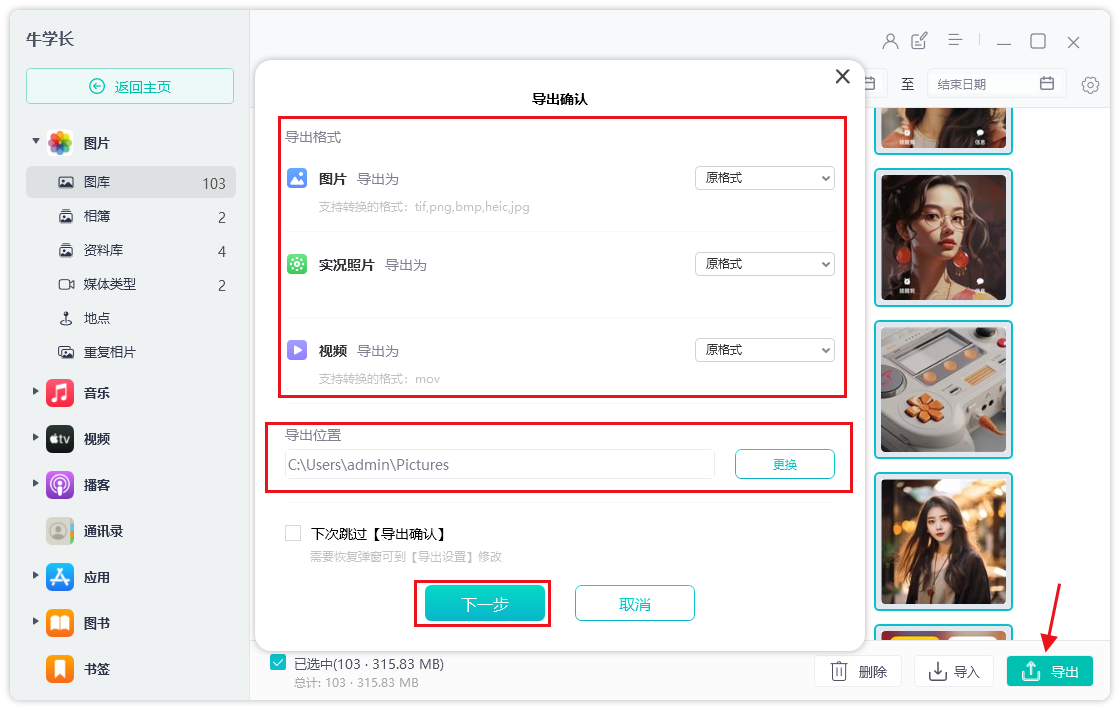
快速将iPhone大量照片快速传输到电脑的办法!
很多使用iPhone 的朋友要将照片传到电脑时,第一时间都只想到用iTunes 或iCloud,但这2个工具真的都非常难用,今天小编分享牛学长苹果数据管理工具的照片传输功能,他可以快速的将iPhone照片传输到电脑上,并且支持最新的i…...

TCP/IP协议簇包含的协议
应用层(Application Layer): HTTP(Hypertext Transfer Protocol):用于Web浏览器和Web服务器之间的通信。HTTPS(Hypertext Transfer Protocol Secure):安全的HTTP版本&…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
