机器学习小白理解之一元线性回归
关于机器学习,百度上一搜一大摞,总之各有各的优劣,有的非常专业,有的看的似懂非懂。我作为一名机器学习的门外汉,为了看懂这些公式和名词真的花了不少时间,还因此去着重学了高数。
不过如果不去看公式,而只去理解机器学习要干的事情,那么就比较容易看懂如何去理解那些公式和专有名词了,下面我以我的一些拙见来理解一下机器学习(全程无公式,只有理解)。
一、假设一个场景
有好多好多珠子要用签子一口气串起来,但不能动珠子,你只能选一个趁手的签子,能尽量多的把珠子串起来,你会选哪个?(插签子的动作必须要帅,只能如下动图的插法)


答案
很显然,我们要选又细又长的签子去插这些珠子,因为这些珠子很明显排的还算整齐,用直直的签子很容易多插到几个。
而这个过程就是需要查看数据样本来确定函数拟合大概是一个怎么样的函数,我们这里就是一个简单的线性函数。
二、插签子
接下来我们就是进行插签子的环节,如果插签子的人很笨,他第一下插下去变成了下面这样:
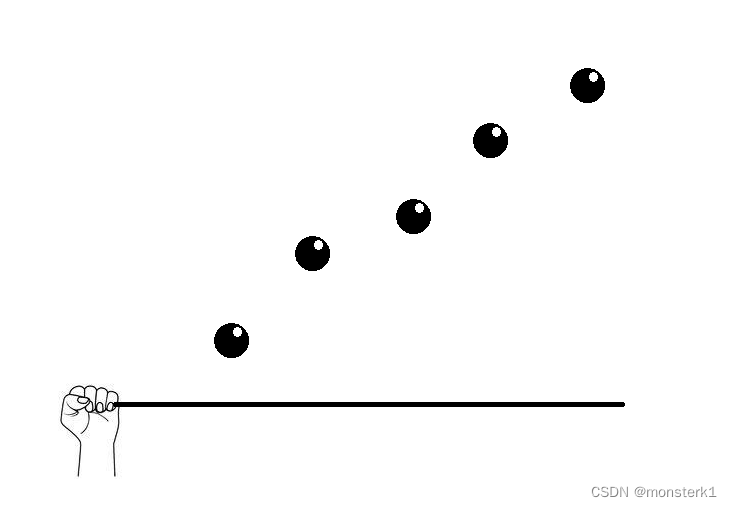
这也太笨了吧,差那么多,嗯,这就是欠拟合,差的太大了,完全插不到一个。
第二次尝试,插成了这个样子:

嗯,比第一次好多了,再来一次:

很好,越来越接近了,再来一次:

完美,这次可以说插的非常漂亮,所以这个插的过程,有人叫它梯度下降,就是为了让签子插过足够多的珠子。
三、大力出奇迹
如果有人大力得很,签子柔韧性又好,就插成了下面这样:

插得很好,签子把每个珠子的圆心都过了,但签子歪了,这就叫过拟合。
四、插签子的角度
在寻找插签子的角度时,我们是通过签子与每个珠子的距离来做判断的:
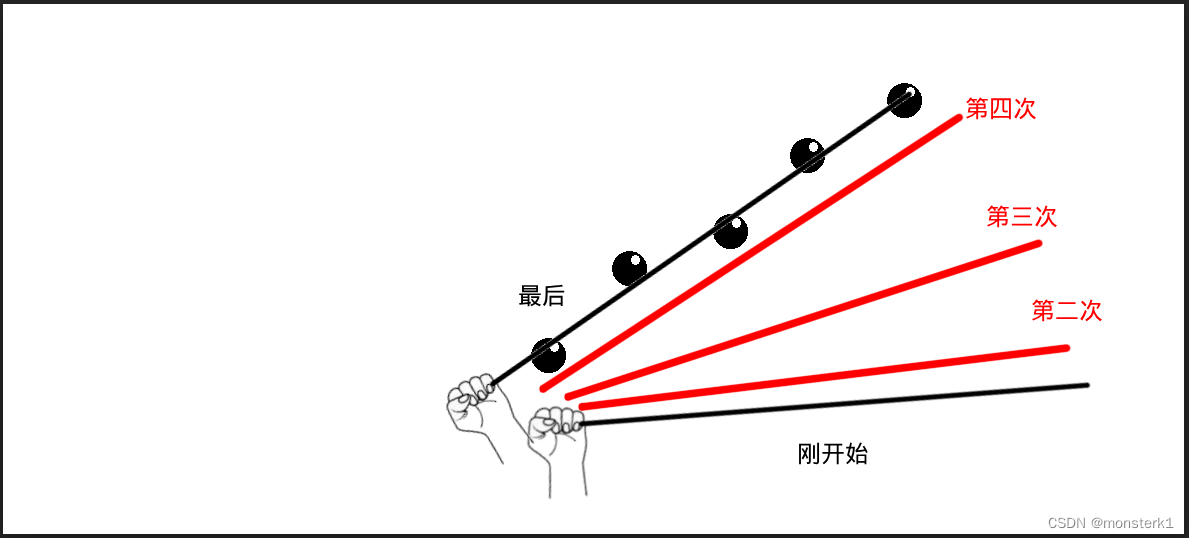 每一次签子和珠子的距离越来越近,是靠肉眼去看的,换到公式中就是我们的代价函数(Cost Function)。
每一次签子和珠子的距离越来越近,是靠肉眼去看的,换到公式中就是我们的代价函数(Cost Function)。
五、总结
以上就是一元线性回归的理解,作为机器学习的入门,一元线性回归是最基础也最基本的。当然,文中的签子只是用来串现有的珠子,而真正的线性回归使用是为了预测结果,上文的场景只是为了表现一元线性回归的思路。
接下来有机会再讨论其他机器学习的内容,通过假设场景来描述机器学习的过程,然后再去看其他更权威的文章,那些公式可能就更容易理解了。
相关文章:

机器学习小白理解之一元线性回归
关于机器学习,百度上一搜一大摞,总之各有各的优劣,有的非常专业,有的看的似懂非懂。我作为一名机器学习的门外汉,为了看懂这些公式和名词真的花了不少时间,还因此去着重学了高数。 不过如果不去看公式&…...

目标检测:FROD: Robust Object Detection for Free
论文作者:Muhammad,Awais,Weiming,Zhuang,Lingjuan,Lyu,Sung-Ho,Bae 作者单位:Sony AI; Kyung-Hee University 论文链接:http://arxiv.org/abs/2308.01888v1 内容简介: 1)方向:目标检测 2)…...
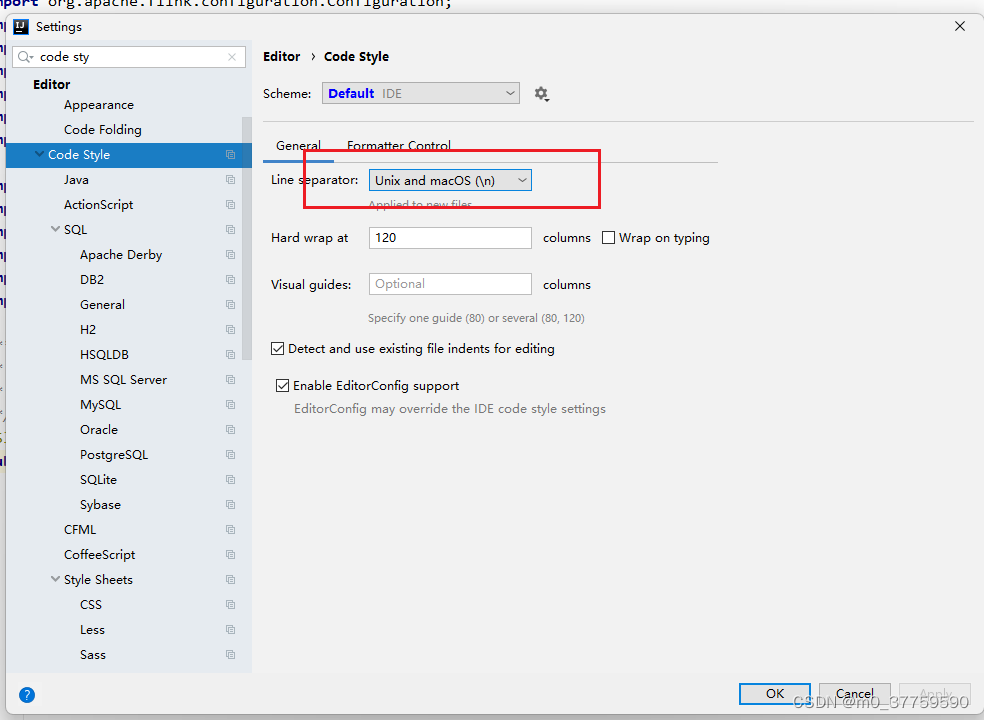
linux 和 windows的換行符不兼容問題
linux 和 windows的換行符: 1.vim 模式下,執行命令: :set ffunix idea中設置code style...
ubuntu 20 安装 CUDA
1. 查看需要安装的cuda版本 nvidia-smi cuda的版本信息如下图所示 2. 去官网下载对应版本的CUDA 官网:CUDA Toolkit Archive | NVIDIA Developer 弹出以下界面,依次点击以下按钮 得到以下内容: 复制下载链接,下载cuda11到本…...

C++友元函数和友元类
友元介绍 类的友元函数是定义在类外部,但有权访问类的所有私有(private)成员和保护(protected)成员。尽管友元函数的原型有在类的定义中出现过,但是友元函数并不是成员函数。 友元可以是一个函数…...
特斯拉——使用人工智能制造智能汽车
特斯拉(Tesla)是电动汽车开发和推广的先驱。特斯拉对自动驾驶汽车的未来寄予厚望--实际上,每一辆特斯拉汽车都有可能通过软件升级成为自动驾驶汽车。该公司还生产和销售高级电池和太阳能电池板。 汽车的自动驾驶是按从1~5的等级划分的。自适应巡航控制和自动停车系…...

如何删除gitlab上多余的文件夹
无意间在提交代码时,包含了多余的 .idea 或者 __pychche__ 缓存文件夹等等,如何一次性删除呢? 实际上没有更好的办法,如果还没有合并,close 掉 MR就行了,重新提交。 如果已经合并了,就会留下记…...

computed和methods有什么区别
面试题:computed和methods有什么区别 标准而浅显的回答 在使用时,computed当做属性使用,而methods则当做方法调用computed可以具有getter和setter,因此可以赋值,而methods不行computed无法接收多个参数,而m…...
、聚集索引、二级索引(索引篇 二))
MySQL索引分类和操作(增删查)、聚集索引、二级索引(索引篇 二)
具体类型索引分类 分类主要作用特点主键索引(primary)针对于表中主键创建的索引默认自动创建, 只能有一个唯一索引(unique)避免同一个表中某数据列中的值重可以有多个常规索引最基本类型,可以加快查询速度可以有多个全文索引(fulltext)查找的是文本中的关键词&…...
(三)Python变量类型和运算符
所有的编程语言都支持变量,Python 也不例外。变量是编程的起点,程序需要将数据存储到变量中。 变量在 Python 内部是有类型的,比如 int、float 等,但是我们在编程时无需关注变量类型,所有的变量都无需提前声明&#x…...

vue三种import导入方式详解?
在Vue.js中,你可以使用三种不同的方式来导入模块或组件: 默认导入 (Default Import): 这种方式用于导入一个模块的默认导出(通常是一个组件或一个对象)。例如: import MyComponent from ./MyComponent.vue;…...

深入理解数据库视图
在数据库管理中,视图(View)是一种强大但常常被忽视的功能。它不仅可以简化复杂的查询操作,还可以提供更高层次的数据抽象和保护。 本文将详细解析视图的各个方面,并以《三国志》游戏的数据为例,给出实际应用场景。 文章目录 什么是视图?基本结构创建视图查看视图的定义…...
方法的作用~)
Java中@before和setup()方法的作用~
在Java中,setup()和Before同时使用的作用是在测试方法之前执行一些准备工作, setup()是JUnit中的一个方法,它通常被用来初始化测试对象和设置测试环境,它会在每个测试方法执行之前被调用,并且可以在多个测试方法中共享…...
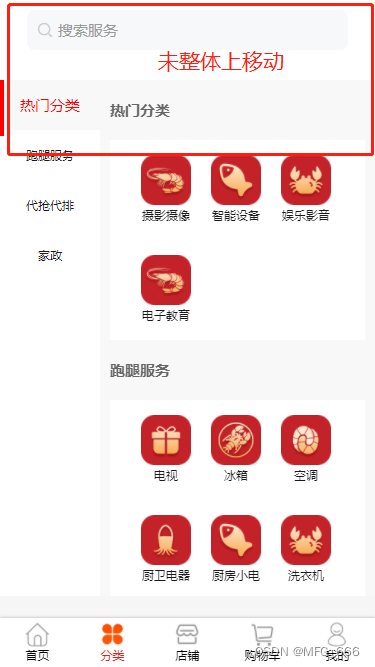
前端uniapp防止页面整体滑动页面顶部以上,设置固定想要固定区域宽高
解决:设置固定想要固定区域宽高 目录 未改前图未改样式改后图改后样式 未改前图 未改样式 .main {display: flex;flex-direction: row;// justify-content: space-between;width: 100vw;// 防止全部移动到上面位置!!!!…...

浮点型数字
1. 浮点型的定义 浮点型(floating-point)是一种表示实数的计算机数据类型,它可以表示有限小数、无限小数和近似值。浮点型的表示方法基于科学计数法,即一个实数可以表示为尾数(有效数字)和指数的乘积。 在…...

贝叶斯统计入门
贝叶斯统计入门 贝叶斯统计是一种以系统和数学严密的方式来推理不确定性的方法。它以18世纪的数学家和哲学家托马斯贝叶斯命名,他开发了一个定理,提供了一种在收集新数据时更新我们对假设的信念的方式。 在贝叶斯统计中,我们从一个先验概率分…...

织梦CMS采集插件-DEDE插件大全
在如今充满信息爆炸的互联网时代,维护一个具有吸引力和活力的网站或博客是一项具有挑战性的任务。对于那些使用织梦CMS建立网站的用户来说,如何持续不断地更新内容以吸引访问者成为了一个突出的问题。 什么是织梦CMS自动采集插件?这些插件是为…...
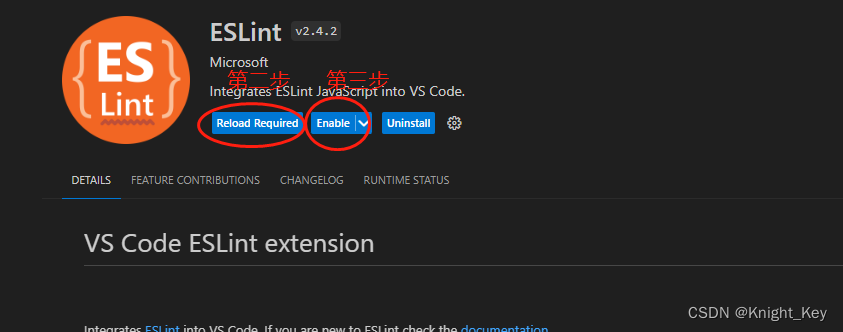
vuereact质检工具(eslint)安装使用总结
1、ESLint ESLint工具主要类似java中的checkStyle和findbugs,是检查代码样式和逻辑规范的工具。 1.1、ESLint安装流程 打开VSCode软件,打开扩展中心,下载ESLint插件 图1.1 点击后面的install按进行安装,如图1.2所示࿱…...

yolox相关
yolox YOLOXYOLOX-DarkNet53yolov3作为baseline输入端Strong data augmentationMosaic数据增强MixUp数据增强注意 BackboneNeckPrediction层Decoupled headDecoupled Head 细节 Anchor-freeAnchor Based方式Anchor Free方式标签分配初步筛选精细化筛选 SimOTASimOTA Other Back…...

递归专题训练详解(回溯,剪枝,深度优先)
1.汉诺塔问题 在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制: (1) 每次只能移动…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
