贝叶斯统计入门
贝叶斯统计入门
贝叶斯统计是一种以系统和数学严密的方式来推理不确定性的方法。它以18世纪的数学家和哲学家托马斯·贝叶斯命名,他开发了一个定理,提供了一种在收集新数据时更新我们对假设的信念的方式。
在贝叶斯统计中,我们从一个先验概率分布开始,它代表了我们在看到任何数据之前对假设的信念。随着我们收集新数据,我们使用贝叶斯定理来更新这个先验分布,得到一个后验概率分布,它代表了在考虑我们观察到的数据后对假设的信念。
例子
为了举例说明,假设我们想要估计在即将举行的选举中将投票给某位候选人的选民比例。
我们首先有一个先验信念,即将投票给该候选人的选民比例在0到1之间是均匀分布的。随着我们收集新数据,比如一次民意调查的结果,我们可以使用贝叶斯定理来更新这个先验分布,得到一个考虑到我们获得的新信息的后验分布。
在贝叶斯统计中,后验分布通常用于进行预测或决策。例如,我们可以使用后验分布来估计某一事件发生的概率,或者决定是否接受或拒绝一个假设。
贝塔分布
在贝叶斯统计中常用的一个概率分布是贝塔分布。它是一个定义在区间[0,1]上的连续概率分布,因此特别适合建模比例或概率。
贝塔分布有两个参数,通常用alpha和beta表示,它们控制了分布的形状。
贝塔分布是二项分布的共轭先验,这意味着如果我们假设我们的数据是由一个具有固定试验次数和未知成功概率的二项分布生成的,并且我们选择贝塔分布作为我们的先验分布,那么后验分布也将是一个贝塔分布。
示例代码
让我们使用贝塔分布来更新我们对硬币抛掷实验的信念,其概率分布是二项分布。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, beta
# 定义真实的成功概率
p_true = 0.7
# 从已知 p_true 的二项分布中生成一些数据
n_trials = 100
data = binom.rvs(n_trials, p_true)
# 定义先验贝塔分布的参数
alpha_prior = 10
beta_prior = 10
# 定义后验贝塔分布的参数
alpha_post = alpha_prior + data
beta_post = beta_prior + n_trials - data
# 创建先验和后验贝塔分布
x = np.linspace(0, 1, 100)
prior = beta(alpha_prior, beta_prior)
posterior = beta(alpha_post, beta_post)
# 绘制先验和后验分布
plt.plot(x, prior.pdf(x), label='先验')
plt.plot(x, posterior.pdf(x), label='后验')
plt.axvline(x=p_true, color='red', linestyle='--', label='真实 p')
plt.legend()
plt.show()
这段代码从一个具有真实成功概率为0.7的二项分布中生成了100次试验。
然后,我们使用alpha=10和beta=10的贝塔分布作为成功概率的先验分布。
我们使用贝叶斯定理将这个先验分布与数据进行了更新,得到的后验分布也是一个贝塔分布。结果图显示了成功概率的先验和后验分布,以及表示真实成功概率的红色垂直线。
从图中可以看出,后验分布向右移动,表示我们现在更有信心硬币偏向正面。
正如图中所示,后验分布向真实的成功概率0.7方向偏移,表明我们已经根据观察到的数据更新了对成功概率的信念。
本文由 mdnice 多平台发布
相关文章:

贝叶斯统计入门
贝叶斯统计入门 贝叶斯统计是一种以系统和数学严密的方式来推理不确定性的方法。它以18世纪的数学家和哲学家托马斯贝叶斯命名,他开发了一个定理,提供了一种在收集新数据时更新我们对假设的信念的方式。 在贝叶斯统计中,我们从一个先验概率分…...

织梦CMS采集插件-DEDE插件大全
在如今充满信息爆炸的互联网时代,维护一个具有吸引力和活力的网站或博客是一项具有挑战性的任务。对于那些使用织梦CMS建立网站的用户来说,如何持续不断地更新内容以吸引访问者成为了一个突出的问题。 什么是织梦CMS自动采集插件?这些插件是为…...
vuereact质检工具(eslint)安装使用总结
1、ESLint ESLint工具主要类似java中的checkStyle和findbugs,是检查代码样式和逻辑规范的工具。 1.1、ESLint安装流程 打开VSCode软件,打开扩展中心,下载ESLint插件 图1.1 点击后面的install按进行安装,如图1.2所示࿱…...

yolox相关
yolox YOLOXYOLOX-DarkNet53yolov3作为baseline输入端Strong data augmentationMosaic数据增强MixUp数据增强注意 BackboneNeckPrediction层Decoupled headDecoupled Head 细节 Anchor-freeAnchor Based方式Anchor Free方式标签分配初步筛选精细化筛选 SimOTASimOTA Other Back…...

递归专题训练详解(回溯,剪枝,深度优先)
1.汉诺塔问题 在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制: (1) 每次只能移动…...

JavaScript系列从入门到精通系列第七篇:JavaScrip当中的运算符,主要涉及JavaScript当中的六大数据类型的四则运算
文章目录 前言 一:算数运算符 1:Number类型的四则运算 2:其他数据类型的四则运算 (一):加法运算 (二):减法运算 3:乘法运算 4:除法运算 5:取模运算 前言 运算符也叫操作符。…...
计算机网络 实验二 交换机的基本配置
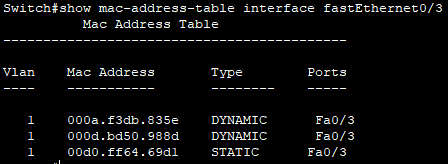
实验二 交换机的基本配置 实验目的 • 掌握交换机的配置方式及切换命令; • 掌握交换机端口的基本配置; • 掌握交换机mac地址的查看与管理方法。 实验设备 以太网交换机一台服务器一台PC机五台配置电缆、网线若干 网络拓扑及IP地址分配 给计算…...

Tor网络的全面解析
一、Tor网络概述 Tor网络,即“洋葱路由器”(The Onion Router),是一种用于保护用户隐私、避免网络监控的开源软件,可以实现匿名访问互联网。 Tor网络通过多重加密和随机转发,将用户的流量从多个节点中进行…...

数据集笔记:2015上海地铁一卡通数据
数据地址:上海地铁数据_免费高速下载|百度网盘-分享无限制 (baidu.com) 数据介绍 上海2015年几天的地铁一卡通出入站信息 卡号、交易日期、交易时间、公交线路/地铁站点中文名称、行业名称(公交、地铁、出租、轮渡、PR停车场)、交易金额、交易性质(非优惠、优惠、…...
【小沐学C++】C++ 基于Premake构建工程项目(Windows)
文章目录 1、简介2、下载和安装2.1 下载2.3 快速入门 3、使用3.1 支持的工程文件Project Files3.2 构建设置Build Settings3.3 链接Linking3.4 配置Configurations3.5 平台Platforms3.6 过滤Filters3.7 预设值Tokens 4、测试4.1 测试1:入门例子4.2 测试2:…...
Linux shell编程学习笔记2:我是谁 | who am i ?
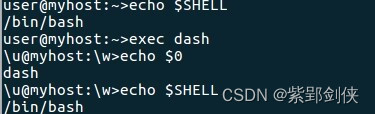
〇、更新记录 20230926 补充例子2 一、前言 由于Linux系统的shell有许多种:sh、bash、cshell、tcsh、zsh……这些shell以sh为基础对象,在保持兼容性时又各有有创建,形成自己的功能特点,要想让我们编写的shell代码正确、可靠运行…...
移动端和PC端对比【组件库+调试vconsole +单位postcss-pxtorem+构建vite/webpack+可视化echarts/antv】
目录 组件库 移动端 vue vant PC端 react antd vue element 调试:vconsole vs dev tools中的控制台(Console) vconsole:在真机上调试 postcss-pxtorem:移动端不同的像素密度 构建工具 webpack 原理 Ba…...

maven多模块依赖包程序包xxx不存在
背景 rpc-common 被 rpc-server、rpc-client依赖 项目地址 https://github.com/pjmike/springboot-rpc-demo mvn clean install 打包时报错 报错信息 程序包xxxx不存在 找不到符号 原因分析 原因还不清楚,网友们帮解答一下 解决 主pom.xml 添加 <packaging…...
iOS17.0.2更新修复iPhone 15系列机型数据迁移问题,附新机快速数据迁移办法!
iPhone 15 系列机型已于今日正式发售,为解决iPhone15这些机型出现的数据迁移问题,苹果紧急发布了 iOS 17.0.2 更新,内部版本号为 21A350。 需要注意的是, iOS 17.0.2 更新仅适用于 iPhone 15、iPhone 15 Plus、iPhone 15 Pro 和 …...
:docker和linux)
面试题库(八):docker和linux
docker docker的原理?dockerfile里面用过什么命令?用过docker?dockerfile写过吗,常用命令,说下分层原理docker 部署有什么好处?docker 的底层原理是什么?namespace 和 cgroups,一个隔离环境,一个控制资源配额。那隔离环境主要隔离什么环境?docker镜像和容器有什么区别…...
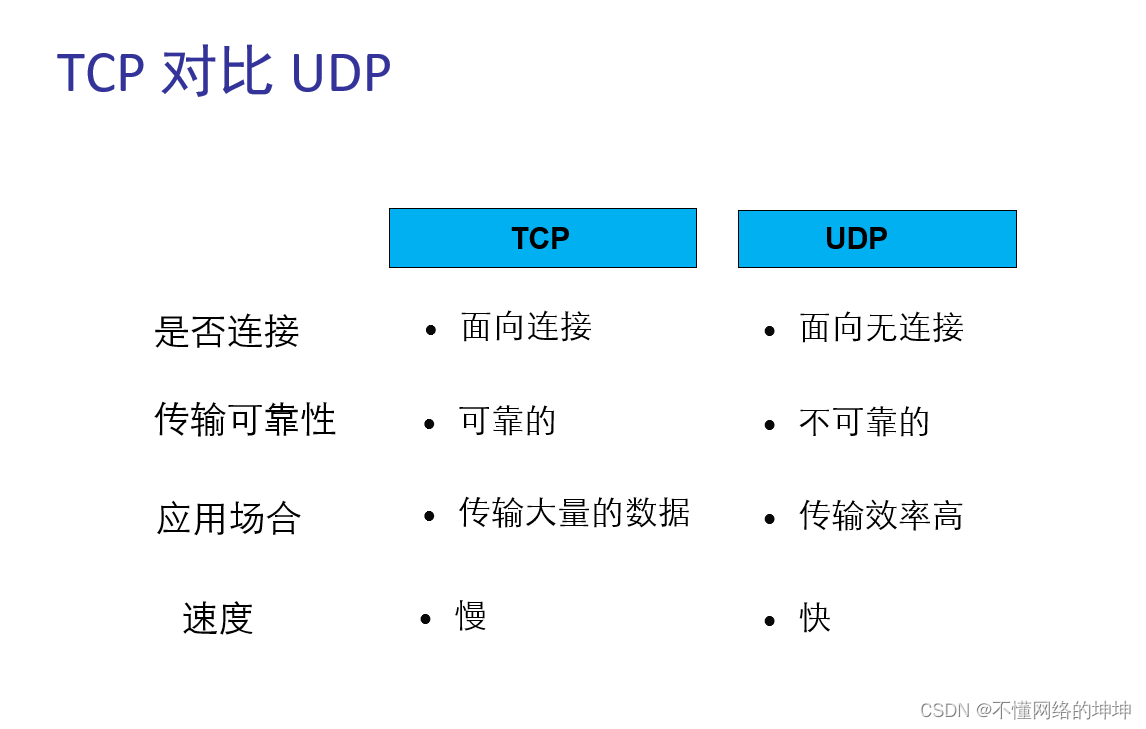
深入理解传输层协议:TCP与UDP的比较与应用
目录 前言什么是TCP/UDPTCP/UDP应用TCP和UDP的对比总结 前言 传输层是TCP/IP协议栈中的第四层,它为应用程序提供服务,定义了主机应用程序之间端到端的连通性。在本文章,我们将深入探讨传输层协议,特别是TCP和UDP协议的原理和区别…...

Python-表白小程序练习
测试代码 在结果导向的今天,切勿眼高于顶,不论用任何方法能转换、拿出实际成果东西才是关键,即使一个制作很简易的程序,你想将其最终生成可运行的版本也是需要下一番功夫的。不要努力成为一个嘴炮成功者,要努力成为一个有价值的人…...

浅谈ChatGPT附免费体验地址
首先,让我来介绍一下ChatGPT是什么。ChatGPT是由OpenAI开发的大型语言模型,它代表着自然语言处理领域的最新进展。这个模型是通过大量的数据和先进的深度学习技术训练而成,具备了强大的语言理解和生成能力。 那么,ChatGPT能做些什…...

队列的使用以及模拟实现(C++版本)
🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨ 🐻强烈推荐优质专栏: 🍔🍟🌯C的世界(持续更新中) 🐻推荐专栏1: 🍔🍟🌯C语言初阶 🐻推荐专栏2: 🍔…...
RV1126笔记四十一:RV1126移植LIVE555
若该文为原创文章,转载请注明原文出处。 RV1126的SDK有提供了一个librtsp.a封装好的RTSP推流库,但不开源,还有个确定延时长,所以想自己写一个RTSP的推流,但不想太麻烦,所以使用Live555。 记录下移植过程和测试结果。 live555需要用到的包有 openssl 和live555 一、 编…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
