【重新定义matlab强大系列十四】基于问题求解有/无约束非线性优化
🔗 运行环境:Matlab
🚩 撰写作者:左手の明天
🥇 精选专栏:《python》
🔥 推荐专栏:《算法研究》
#### 防伪水印——左手の明天 ####
💗 大家好🤗🤗🤗,我是左手の明天!好久不见💗
💗今天开启新的系列——重新定义matlab强大系列💗
📆 最近更新:2023 年 09 月 23 日,左手の明天的第 291 篇原创博客
📚 更新于专栏:matlab
#### 防伪水印——左手の明天 ####
约束优化定义
约束最小化问题求向量 x,在满足 x 取值约束的前提下,使得标量函数 f(x) 取得局部最小值:
![]()
使得以下一项或多项成立:c(x) ≤ 0, ceq(x) = 0, A·x ≤ b, Aeq·x = beq, l ≤ x ≤ u。
基于问题求解非线性优化
通过使用基于问题的方法寻找具有非线性约束的非线性目标函数的最小值。要使用基于问题的方法找到非线性目标函数的最小值,首先将目标函数编写为文件或匿名函数。目标函数是
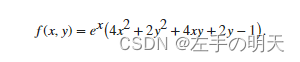
type objfunxfunction f = objfunx(x,y)
f = exp(x).*(4*x.^2 + 2*y.^2 + 4*x.*y + 2*y - 1);
end创建优化问题变量 x 和 y。
x = optimvar('x');
y = optimvar('y');使用优化变量的表达式创建目标函数。
obj = objfunx(x,y);创建一个以 obj 为目标函数的优化问题。
prob = optimproblem('Objective',obj);创建一个使解位于倾斜椭圆中的非线性约束,指定为

使用优化变量的不等式表达式创建约束。
TiltEllipse = x.*y/2 + (x+2).^2 + (y-2).^2/2 <= 2;在问题中包含该约束。
prob.Constraints.constr = TiltEllipse;创建一个结构体,将初始点表示为 x = –3、y = 3。
x0.x = -3;
x0.y = 3;检查此问题。
show(prob)OptimizationProblem : Solve for:x, yminimize :(exp(x) .* (((((4 .* x.^2) + (2 .* y.^2)) + ((4 .* x) .* y)) + (2 .* y)) - 1))subject to constr:((((x .* y) ./ 2) + (x + 2).^2) + ((y - 2).^2 ./ 2)) <= 2求解。
[sol,fval] = solve(prob,x0)Solving problem using fmincon.Local minimum found that satisfies the constraints.Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
sol = struct with fields:x: -5.2813y: 4.6815fval = 0.3299尝试不同起点。
x0.x = -1;
x0.y = 1;
[sol2,fval2] = solve(prob,x0)Solving problem using fmincon.Feasible point with lower objective function value found.Local minimum found that satisfies the constraints.Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.sol2 = struct with fields:x: -0.8210y: 0.6696fval2 = 0.7626绘制椭圆、目标函数等高线和两个解。
f = @objfunx;
g = @(x,y) x.*y/2+(x+2).^2+(y-2).^2/2-2;
rnge = [-5.5 -0.25 -0.25 7];
fimplicit(g,'k-')
axis(rnge);
hold on
fcontour(f,rnge,'LevelList',logspace(-1,1))
plot(sol.x,sol.y,'ro','LineWidth',2)
plot(sol2.x,sol2.y,'ko','LineWidth',2)
legend('Constraint','f Contours','Global Solution','Local Solution','Location','northeast');
hold off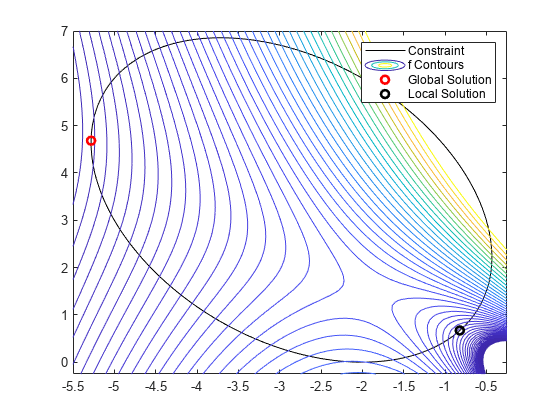
解位于非线性约束边界上。等高线图显示这些是仅有的局部最小值。该图还显示在 [–2,3/2] 附近存在一个平稳点,在 [–2,0] 和 [–1,4] 附近存在局部最大值。
Matlab求解函数
求解无约束极小值
基于求解器求解
在matlab工具箱中,用于求解无约束极小值问题的函数有 fminunc 和 fminsearch (局部最优化算法):
fminunc(采用拟牛顿法(QN),是一种使用导数的算法)
[x, fval, exitflag, output, grad, hessian] = fminunc(fun, x0, options)
输入参数:
- fun 为要计算最小值的函数;
- x0 为初始点;
- options 为优化选项。
输出参数:
- x 为解,
- fval 为解处的目标函数值;
- exitflag 为fminunc 停止的原因,
- output 为有关优化过程的信息,
- grad 为解处的梯度,
- hessian 为逼近 Hessian 矩阵。
最小化函数:
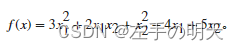
fun = @(x)3*x(1)^2 + 2*x(1)*x(2) + x(2)^2 - 4*x(1) + 5*x(2);调用 fminunc 以在 [1,1] 附近处求 fun 的最小值。
x0 = [1,1];
[x,fval] = fminunc(fun,x0)Local minimum found.Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.x = 1×22.2500 -4.7500fval = -16.3750fminsearch(采用Nelder-Mead单纯形法,是一种直接搜索法)
[x, fval, exitflag, output, grad, hessian] = fminunc(fun, x0, options)
输入参数:
- fun 为要计算最小值的函数;
- x0 为初始点;
- options 为优化选项。
输出参数:
- x 为解,
- fval 为解处的目标函数值;
- exitflag 为fminunc 停止的原因,
- output 为有关优化过程的信息。
监视优化过程
options = optimset('PlotFcns',@optimplotfval);将目标函数设置为 Rosenbrock 函数,

该函数的最小值在 x = [1,1] 处,最小值为 0。
将起始点设置为 x0 = [-1.2,1] 并使用 fminsearch 计算 Rosenbrock 函数的最小值。
fun = @(x)100*(x(2) - x(1)^2)^2 + (1 - x(1))^2;
x0 = [-1.2,1];
x = fminsearch(fun,x0,options)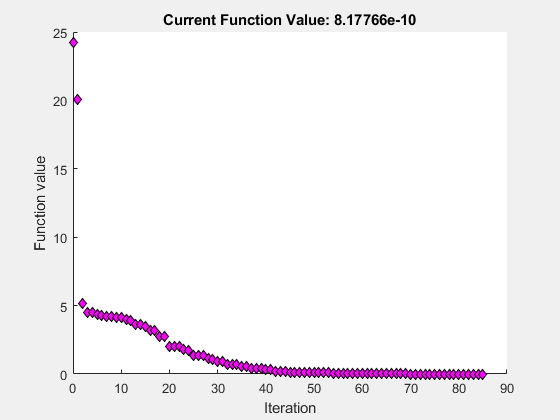
x = 1×21.0000 1.0000检查优化过程
在优化进行期间和优化结束后检查优化结果。
将选项设置为提供迭代输出,从而在求解器运行时提供有关优化的信息。此外,将绘图函数设置为在求解器运行时显示目标函数值。
options = optimset('Display','iter','PlotFcns',@optimplotfval);设置目标函数和起始点。
function f = objectivefcn1(x)
f = 0;
for k = -10:10f = f + exp(-(x(1)-x(2))^2 - 2*x(1)^2)*cos(x(2))*sin(2*x(2));
end将 objectivefcn1 的代码作为文件包含在路径中。
x0 = [0.25,-0.25];
fun = @objectivefcn1;获取所有求解器输出。在求解器运行完毕后,使用这些输出检查结果。
[x,fval,exitflag,output] = fminsearch(fun,x0,options)Iteration Func-count f(x) Procedure0 1 -6.70447 1 3 -6.89837 initial simplex2 5 -7.34101 expand3 7 -7.91894 expand4 9 -9.07939 expand5 11 -10.5047 expand6 13 -12.4957 expand7 15 -12.6957 reflect8 17 -12.8052 contract outside9 19 -12.8052 contract inside10 21 -13.0189 expand11 23 -13.0189 contract inside12 25 -13.0374 reflect13 27 -13.122 reflect14 28 -13.122 reflect15 29 -13.122 reflect16 31 -13.122 contract outside17 33 -13.1279 contract inside18 35 -13.1279 contract inside19 37 -13.1296 contract inside20 39 -13.1301 contract inside21 41 -13.1305 reflect22 43 -13.1306 contract inside23 45 -13.1309 contract inside24 47 -13.1309 contract inside25 49 -13.131 reflect26 51 -13.131 contract inside27 53 -13.131 contract inside28 55 -13.131 contract inside29 57 -13.131 contract outside30 59 -13.131 contract inside31 61 -13.131 contract inside32 63 -13.131 contract inside33 65 -13.131 contract outside34 67 -13.131 contract inside35 69 -13.131 contract insideOptimization terminated:the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-04 and F(X) satisfies the convergence criteria using OPTIONS.TolFun of 1.000000e-04
x =-0.1696 -0.5086fval =-13.1310exitflag =1output = struct with fields:iterations: 35funcCount: 69algorithm: 'Nelder-Mead simplex direct search'message: 'Optimization terminated:...'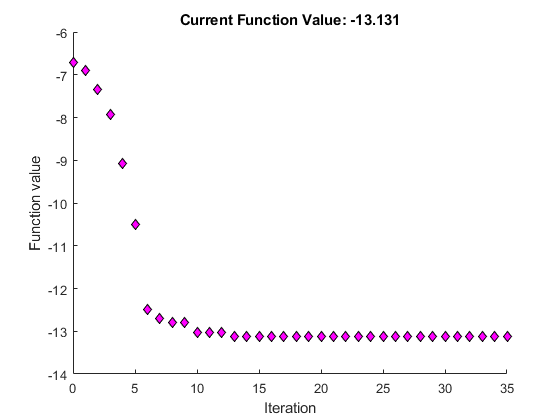
exitflag 的值为 1,这意味着 fminsearch 很可能收敛于局部最小值。
output 结构体显示迭代数。迭代输出中和绘图中也显示此信息。output 结构体还显示函数求值的次数,迭代输出方式会显示该次数,但所选的绘图函数不显示该次数。
基于问题求解
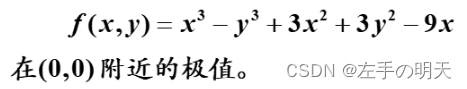
(1)基于求解器求解
clc, clear
f=@(x) x(1)^3-x(2)^3+3*x(1)^2+3*x(2)^2-9*x(1);
g=@(x) -f(x);
[xy1,z1]=fminunc(f, rand(2,1)) %求极小值点
[xy2,z2]=fminsearch(g,rand(2,1)); %求极大值点
xy2, z2=-z2 %显示极大点及对应的极大值
(2)基于问题求解
clc, clear, prob1=optimproblem; %最小值问题
x=optimvar('x','LowerBound',-3,'UpperBound',3);
y=optimvar('y','LowerBound',-4,'UpperBound',4);
prob1.Objective=x^3-y^3+3*x^2+3*y^2-9*x;
x0.x=1; x0.y=1;
[sol1,fval1,flag1,out1]=solve(prob1,x0)
prob2=optimproblem('ObjectiveSense','max')
prob2.Objective=x^3-y^3+3*x^2+3*y^2-9*x;
op=optimoptions(@fmincon,'Algorithm','active-set')
[sol2,fval2,flag2,out2]=solve(prob2,x0,'Options',op)
求得的极小值点为 (1,0),极小值为 -5;极大值点为 (-3,2),极大值为 31。
求解有约束极小值
基于求解器求解
非线性规划模型的一般形式为
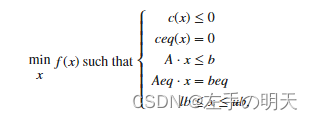
b 和 beq 是向量,A 和 Aeq 是矩阵,c(x) 和 ceq(x) 是返回向量的函数,f(x) 是返回标量的函数。f(x)、c(x) 和 ceq(x) 可以是非线性函数。
x、lb 和 ub 可以作为向量或矩阵传递。
fmincon(寻找约束非线性多变量函数的最小值)
[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)输入参数:
- fun 为要计算最小值的函数
- x0 为初始点,指定为实数向量或实数数组。求解器使用 x0 的大小以及其中的元素数量确定 fun 接受的变量数量和大小。
- A 为线性不等式约束矩阵,A 表示约束中的线性系数;
- b 为线性不等式约束向量,b 表示约束中的常向量;
- Aeq 为线性等式约束矩阵,beq 为线性等式约束向量;
- lb 为下界,ub 为上界;
- nonlcon 为非线性约束;
- options 为 intlinprog 的选项,
- problem 为封装输入和选项的结构体,
- lambda 为解处的拉格朗日乘数,
- grad 为解处的梯度,
- hessian 为逼近 Hessian 矩阵
输出参数:
- x 为解
- fval 为目标函数最优值;
- exitflag 为算法停止条件,
- output 为求解过程摘要。
在非线性约束下求函数的最小值
在边界约束下求 Rosenbrock 函数在圆内最小的点。
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;在区域
![]()
![]()
内寻找。
lb = [0,0.2];
ub = [0.5,0.8];同时在以 [1/3,1/3] 为圆心、半径为 1/3 的圆内寻找。
function [c,ceq] = circlecon(x)
c = (x(1)-1/3)^2 + (x(2)-1/3)^2 - (1/3)^2;
ceq = [];
没有线性约束,因此将这些参数设置为 []。
A = [];
b = [];
Aeq = [];
beq = [];选择一个满足所有约束的初始点。
x0 = [1/4,1/4];
求解。
nonlcon = @circlecon;
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)Local minimum found that satisfies the constraints.Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.x =0.5000 0.2500基于问题求解
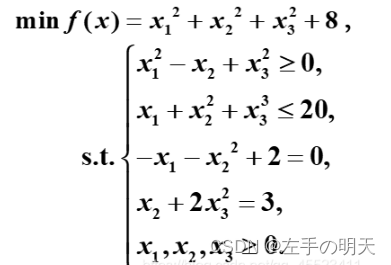
(1)基于求解器求解
clc, clear
fun1 = @(x) sum(x.^2)+8;
[x,y]=fmincon(fun1,rand(3,1),[],[],[],[],zeros(3,1),[],@fun2)function [c,ceq]=fun2(x)
c=[-x(1)^2+x(2)-x(3)^2
x(1)+x(2)^2+x(3)^3-20]; %非线性不等式约束
ceq=[-x(1)-x(2)^2+2
x(2)+2*x(3)^2-3]; %非线性等式约束
end(2)基于问题求解
clc, clear, prob = optimproblem;
x = optimvar('x',3,'LowerBound',0);
prob.Objective = sum(x.^2)+8;
con1 = [-x(1)^2+x(2)-x(3)^2 <= 0
x(1)+x(2)^2+x(3)^3 <= 20]; %非线性不等式约束
con2 = [-x(1)-x(2)^2+2 == 0x(2)+2*x(3)^2 == 3]; %非线性等式约束
prob.Constraints.con1 = con1;
prob.Constraints.con2 = con2;
x0.x=rand(3,1); %非线性规划必须赋初值
[sol,fval,flag,out]= solve(prob,x0), sol.x
求得当 x1 = 0.5522, x2 = 1.2033, x3 = 0.9478 时,最小值 y = 10.6511。
相关文章:
【重新定义matlab强大系列十四】基于问题求解有/无约束非线性优化
🔗 运行环境:Matlab 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 #### 防伪水印——左手の明天 #### 💗 大家好🤗ᾑ…...

MySQL 索引介绍和最佳实践
目录 一、前言二、索引类型1.1 主键索引(PRIMARY KEY)1.2 唯一索引(UNIQUE)1.3 普通索引(NORMAL)1.3.1 单列普通索引1.3.2 单列前缀普通索引1.3.3 多列普通索引1.3.4 多列前缀普通索引 1.4 空间索引&#x…...
:p2p去中心化之初始化websoket服务端)
区块链(7):p2p去中心化之初始化websoket服务端
1 整个流程梳理 服务开启onStart()连接打开onOpen()处理接收到的消息onMesage()连接关闭onClose()异常处理onError()2 创建p2p实现类 package com.example.demo.service;import com.example.demo.entity.BlockChain; import org.java_websocket.WebSocket; import org.java_we…...

原型、原型链、判断数据类型
目录 作用 原型链 引用类型:__proto__(隐式原型)属性,属性值是对象函数:prototype(原型)属性,属性值是对象 Function:本身也是函数 相关方法 person.prototype.isPrototypeOf(stu) Object.getPrototypeOf(objec…...
pycharm中配置torch
在控制台cmd中安装好torch后,在pycharm中使用torch,需要进行简单设置即可。 在pycharm中新建一个工程,在file文件中打开setting 在setting中找到project interpreter编译器 找到conda environment的环境配置,设置好相应的目录 新…...
什么是Times New Roman 字体
如何评价 Times New Roman 字体?:https://www.zhihu.com/question/24614549?sortcreated 新罗马字体是Times New Roman字体,是Office Word默认自带的英文字体之一。 中英文字体 写作中,英文和数字的标准字体为 Times New Roma…...

企业会议新闻稿怎么写?会议类新闻稿如何撰写?
企业会议新闻稿是企业对外传递信息的重要途径之一,它能够将企业的决策、动态以及成果展示给公众。本文伯乐网络传媒将详细解析企业会议新闻稿的写作要点和技巧,以及常见问题及解决方法,帮助大家更好地完成企业会议新闻稿的撰写工作。 一、企业…...
)
算法 滑动窗口最大值-(双指针+队列)
牛客网: BM45 题目: 数组num, 窗口大小size, 所有窗口内的最大值 思路: 用队列作为窗口,窗口内存储数组坐标,left window[0], right从数组0开始遍历完数组,每次新增元素时,(1)先对窗口大小进行收缩到size大小范围,即…...

Java 并发编程面试题——BlockingQueue
目录 1.什么是阻塞队列 (BlockingQueue)?2.BlockingQueue 有哪些核心方法?3.BlockingQueue 有哪些常用的实现类?3.1.ArrayBlockingQueue3.2.DelayQueue3.3.LinkedBlockingQueue3.4.PriorityBlockingQueue3.5.SynchronousQueue 4.✨BlockingQu…...

Ubuntu Nacos开机自启动服务
1、创建service文件 在/lib/systemd/system目录下创建nacos.service文件 [Unit] Descriptionalibaba nacos Afternetwork.target Documentationhttps://nacos.io/zh-cn/[Service] Userroot Grouproot Typeforking Environment"JAVA_HOME/usr/local/programs/jdk-8u333-li…...

C++核心编程--继承篇
4.6、继承 继承是面向对象三大特征之一 有些类与类之间存在特殊的关系,例如下图中: 我们发现,定义这些类的定义时,都拥有上一级的一些共性,还有一些自己的特性。那么我们遇到重复的东西时,就可以考虑使…...

小程序 解决自定义弹窗滚动穿透问题,解决弹窗背景内容滚动问题
方法一、catchtouchmove"true", 可以实现弹框背景不滚动,但是也会导致弹框自身无法滚动,如果你的弹窗本身是不需要滚动的,用这个方法是极佳的。 <view class"pop" catchtouchmove"true"> …...
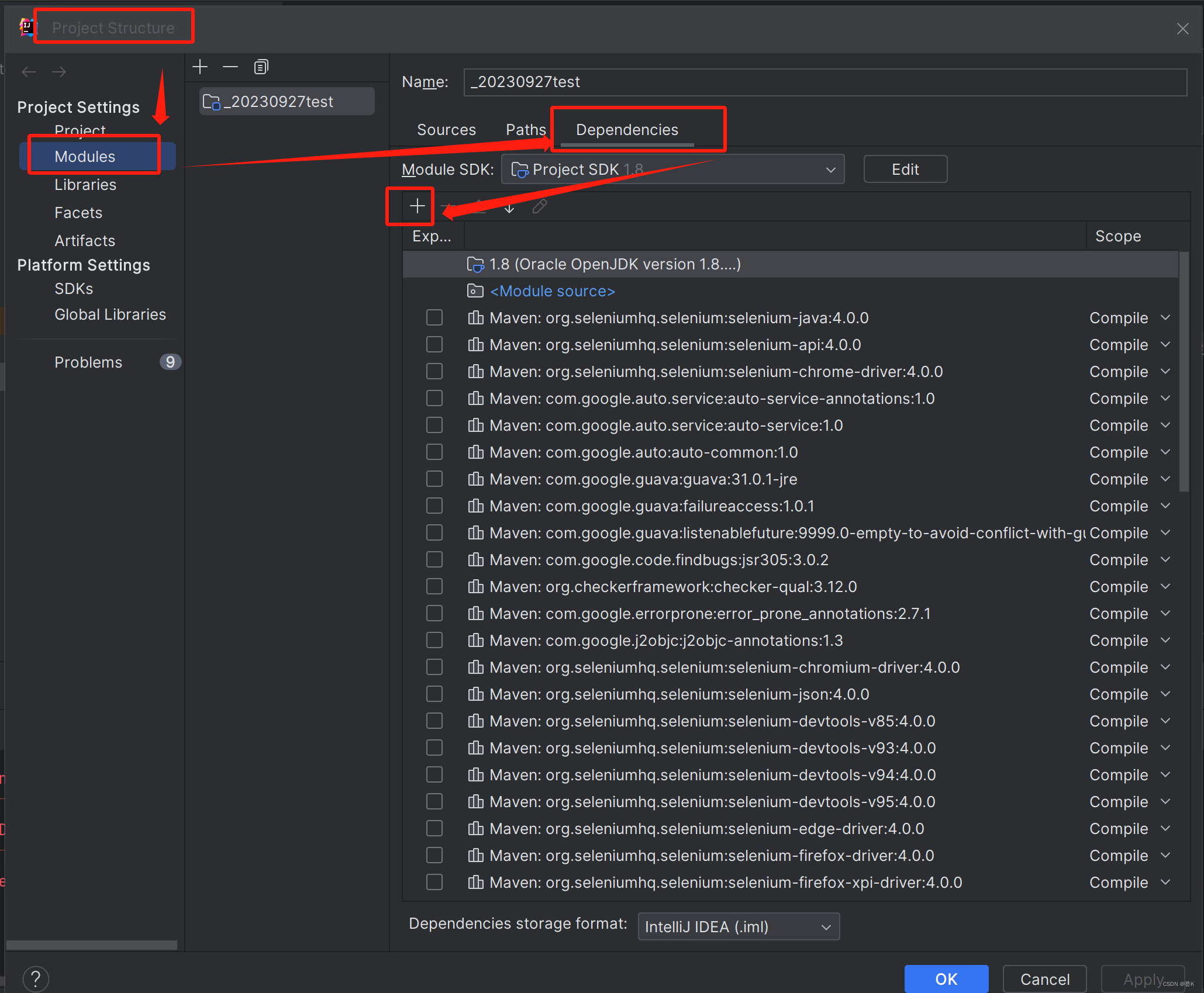
win10搭建Selenium环境+java+IDEA(2)
接着上一个搭建环境开始叙述:win10系统x64安装java环境以及搭建自动化测试环境_荟K的博客-CSDN博客 上一步结尾的浏览器驱动,本人后面改到了谷歌浏览器.exe文件夹下: 这里需要注意,这个新路径要加载到系统环境变量中。 上一步下…...

抢先一步感受未来:Raspberry Pi 5正式发布!
在经历了几年全球供应链困境导致 Raspberry Pi 单板计算机的产能降低和零售价格上涨之后,今天终于迎来了更新。Raspberry Pi 4 上市四年后,今天Raspberry Pi 5正式发布!新推出的 Raspberry Pi 5 配备了经过大幅改进升级的SoC,带来…...

【教程】Ubuntu自动查看有哪些用户名与密码相同的账户,并统一修改密码
转载请注明出处:小锋学长生活大爆炸[xfxuezhagn.cn] 目录 背景说明 开始操作 修改密码 背景说明 有些用户为了图方便或者初始创建用户默认设置等原因,会将密码设置为与用户名相同,但这就使得非常不安全。甚至如果该用户具有sudo权限&#…...
基于 Python+DenseNet121 算法模型实现一个图像分类识别系统
项目展示 一、介绍 DenseNet(Densely Connected Convolutional Networks)是一种卷积神经网络(CNN)架构,2017年由Gao Huang等人提出。该网络的核心思想是密集连接,即每一层都接收其前面所有层的输出作为输…...

贪心算法-点灯问题
1、题目描述 给定一个字符串str,只由 ‘X’ 和 ‘.’ 两种字符构成。‘X’ 表示墙,不能放灯,点亮不点亮都可;’.’ 表示居民点,可以放灯,需要点亮。如果灯放在i位置,可以让 i-1,i 和…...
软件测试之单元测试自动化入门基础
单元测试自动化 所谓的单元测试(Unit Test)是根据特定的输入数据,针对程序代码中的最小实体单元的输入输出的正确性进行验证测试的过程。所谓的最小实体单元就是组织项目代码的最基本代码结构:函数,类,模块等。在Python中比较知名…...
93 # 实现 express 错误处理中间件
上一节实现了 express 的中间件,这一节来实现错误处理中间件 执行某一步出错了,统一规定调用 next 传递的参数就是错误信息 先看 express 实现的demo const express require("express"); const app express();app.use("/", (re…...

PHP 创建 MySQL 表
目录 PHP 创建 MySQL 表 使用 MySQLi 和 PDO 创建 MySQL 表 实例 (MySQLi - 面向对象) 实例 (MySQLi - 面向过程) 实例 (PDO) PHP 创建 MySQL 表 一个数据表有一个唯一名称,并有行和列组成。 使用 MySQLi 和 PDO 创建 MySQL 表 CREATE TABLE 语句用于创建 MySQ…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
