估计、偏差和方差
一、介绍
统计领域为我们提供了很多工具来实现机器学习目标,不仅可以解决训练集上的任务,还可以泛化。基本的概念,例如参数估计、偏差和方差,对于正式地刻画泛化、欠拟合和过拟合都非常有帮助。
二、参数估计
参数估计 是统计学中的一个关键概念,它涉及估计概率分布中的参数值,以便能够对总体或随机过程进行描述或预测。参数估计通常分为两个主要类型:点估计和区间估计。
-
点估计(Point Estimation):
- 点估计旨在找到单个值,该值代表未知参数的“最佳猜测”。这个值通常是一个统计样本的函数。
- 常见的点估计方法包括最大似然估计(Maximum Likelihood Estimation,MLE)和最小二乘估计(Least Squares Estimation),它们都用于估计参数值。
- 例如,如果你想估计某个总体的均值或方差,样本均值和样本方差可以分别用作点估计。
-
区间估计(Interval Estimation):
- 区间估计涉及到估计参数值的范围,而不是单个点。这个范围通常以置信区间的形式表示。
- 置信区间告诉你参数值落在一个特定的区间内的概率有多大。典型的置信水平是95%,这意味着在多次抽样中,大约95%的区间会包含真实参数值。
- 区间估计提供了估计的不确定性度量,相比于点估计更具信息量
三、点估计
点估计(Point Estimation) 是统计学中的一种方法,用于估计未知参数的单个值,通常是一个统计样本的函数。点估计的目标是找到一个估计值,该估计值可以代表未知参数的"最佳猜测",尽管它可能不会精确地等于真实参数值。

点估计涉及以下关键概念:
-
参数: 在统计学中,参数是描述总体分布或概率分布的特征,例如均值、方差、概率等。点估计的目标通常是估计这些参数的值。
-
估计量: 估计参数值的统计量被称为估计量。估计量通常是基于样本数据计算的函数,用于估计总体参数。
-
点估计值: 点估计值是估计量的具体值,它代表了对参数的估计。这是一个单个数值,通常是样本数据的函数。
点估计的常见例子包括:
-
样本均值估计总体均值: 如果你想估计某个总体的均值,可以使用样本均值作为点估计,即将样本数据的平均值作为总体均值的估计值。
-
样本方差估计总体方差: 如果你希望估计总体的方差,可以使用样本方差作为点估计,即将样本数据的方差作为总体方差的估计值。
-
二项分布的成功概率估计: 如果你想估计二项分布中成功的概率(例如投硬币正面的概率),可以使用成功的样本比例作为点估计。
需要注意的是,点估计提供了对参数的单个估计值,但并不提供关于估计的精确性或可信度的信息。为了更全面地了解估计的可信度,通常还会进行区间估计和假设检验等进一步的统计分析。点估计在统计学中是一个基础而重要的概念,它为估计未知参数提供了一种简单而直观的方法。
三、常用的点估计方法
常用的点估计方法有以下几种:
1. 最大似然估计(Maximum Likelihood Estimation, MLE):基于样本数据的概率分布模型,寻找参数值,使得给定样本观测到的概率最大。
2. 最小二乘估计(Least Squares Estimation, LSE):通过最小化样本观测值与模型预测值之间的平方差,来估计参数值。
3. 矩估计法(Method of Moments, MOM):通过将样本矩与理论矩相等,来求解参数的估计值。
4. 贝叶斯估计(Bayesian Estimation):基于贝叶斯定理,结合先验信息和样本信息,得到参数的后验分布,并通过后验分布来进行参数估计。
四、偏差
在统计学中,偏差是指参数估计的期望值与真实参数值之间的差异。简而言之,它表示估计值在平均情况下离真实值有多远。一个无偏的估计是指其期望值等于真实参数值。如果估计的期望值与真实值有偏差,那么这个估计就是有偏的。有偏估计在某些情况下可能更准确,但在其他情况下可能不准确。


五、方差和标准差
方差(Variance) 和 标准差(Standard Deviation) 都是用于衡量数据分布或随机变量离散程度的统计指标,它们之间有密切的关系。
-
方差是一组数据的离散程度的度量,它表示数据点与数据集均值之间的差异程度的平方平均值。方差越大,表示数据点更分散,离均值越远。
-
标准差是方差的平方根,它衡量了数据的离散程度,但以与原始数据相同的单位来表示。标准差通常更容易理解,因为它与原始数据的尺度一致。
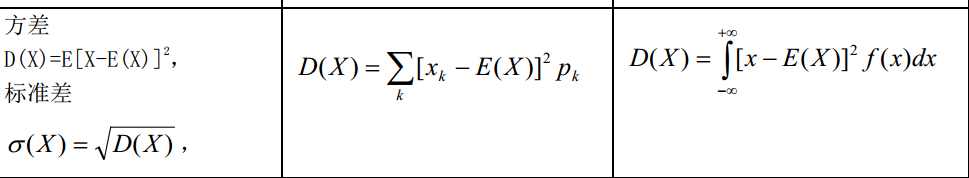
方差和标准差的应用:
-
方差和标准差常用于描述数据的离散程度。如果数据的方差或标准差较大,说明数据点分布较分散;如果它们较小,说明数据点较接近均值。
-
在统计学和机器学习中,方差和标准差用于衡量模型的性能和稳定性。例如,模型的预测误差的方差可以用来评估模型的稳定性,较小的方差表示模型更一致地预测。
参考:
概率论:参数估计——点估计_李小星同志的博客-CSDN博客
《统计推断》整理3:点估计 - 知乎
相关文章:
估计、偏差和方差
一、介绍 统计领域为我们提供了很多工具来实现机器学习目标,不仅可以解决训练集上的任务,还可以泛化。基本的概念,例如参数估计、偏差和方差,对于正式地刻画泛化、欠拟合和过拟合都非常有帮助。 二、参数估计 参数估计 是统计学…...
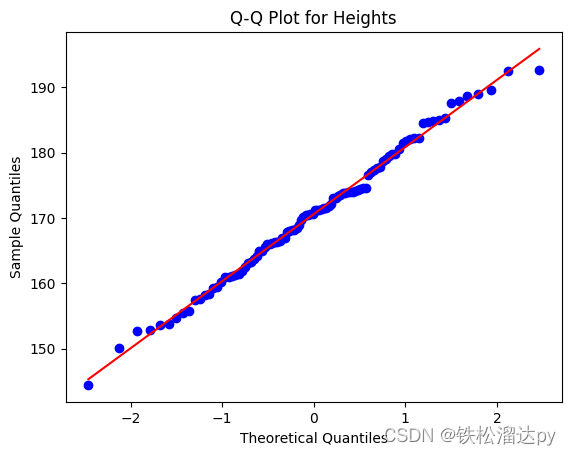
正态分布的概率密度函数|正态分布检验|Q-Q图
正态分布的概率密度函数(Probability Density Function,简称PDF)的函数取值是指在给定的正态分布参数(均值 μ 和标准差 σ)下,对于特定的随机变量取值 x,计算得到的概率密度值 f(x)。这个值表示…...
【接口测试】HTTP协议
一、HTTP 协议基础 HTTP 简介 HTTP 是一个客户端终端(用户)和服务器端(网站)请求和应答的标准(TCP)。通常是由客户端发起一个请求,创建一个到服务器的 TCP 连接,当服务器监听到客户…...
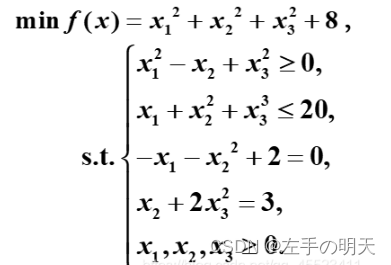
【重新定义matlab强大系列十四】基于问题求解有/无约束非线性优化
🔗 运行环境:Matlab 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 #### 防伪水印——左手の明天 #### 💗 大家好🤗ᾑ…...

MySQL 索引介绍和最佳实践
目录 一、前言二、索引类型1.1 主键索引(PRIMARY KEY)1.2 唯一索引(UNIQUE)1.3 普通索引(NORMAL)1.3.1 单列普通索引1.3.2 单列前缀普通索引1.3.3 多列普通索引1.3.4 多列前缀普通索引 1.4 空间索引&#x…...
:p2p去中心化之初始化websoket服务端)
区块链(7):p2p去中心化之初始化websoket服务端
1 整个流程梳理 服务开启onStart()连接打开onOpen()处理接收到的消息onMesage()连接关闭onClose()异常处理onError()2 创建p2p实现类 package com.example.demo.service;import com.example.demo.entity.BlockChain; import org.java_websocket.WebSocket; import org.java_we…...

原型、原型链、判断数据类型
目录 作用 原型链 引用类型:__proto__(隐式原型)属性,属性值是对象函数:prototype(原型)属性,属性值是对象 Function:本身也是函数 相关方法 person.prototype.isPrototypeOf(stu) Object.getPrototypeOf(objec…...
pycharm中配置torch
在控制台cmd中安装好torch后,在pycharm中使用torch,需要进行简单设置即可。 在pycharm中新建一个工程,在file文件中打开setting 在setting中找到project interpreter编译器 找到conda environment的环境配置,设置好相应的目录 新…...
什么是Times New Roman 字体
如何评价 Times New Roman 字体?:https://www.zhihu.com/question/24614549?sortcreated 新罗马字体是Times New Roman字体,是Office Word默认自带的英文字体之一。 中英文字体 写作中,英文和数字的标准字体为 Times New Roma…...

企业会议新闻稿怎么写?会议类新闻稿如何撰写?
企业会议新闻稿是企业对外传递信息的重要途径之一,它能够将企业的决策、动态以及成果展示给公众。本文伯乐网络传媒将详细解析企业会议新闻稿的写作要点和技巧,以及常见问题及解决方法,帮助大家更好地完成企业会议新闻稿的撰写工作。 一、企业…...
)
算法 滑动窗口最大值-(双指针+队列)
牛客网: BM45 题目: 数组num, 窗口大小size, 所有窗口内的最大值 思路: 用队列作为窗口,窗口内存储数组坐标,left window[0], right从数组0开始遍历完数组,每次新增元素时,(1)先对窗口大小进行收缩到size大小范围,即…...

Java 并发编程面试题——BlockingQueue
目录 1.什么是阻塞队列 (BlockingQueue)?2.BlockingQueue 有哪些核心方法?3.BlockingQueue 有哪些常用的实现类?3.1.ArrayBlockingQueue3.2.DelayQueue3.3.LinkedBlockingQueue3.4.PriorityBlockingQueue3.5.SynchronousQueue 4.✨BlockingQu…...

Ubuntu Nacos开机自启动服务
1、创建service文件 在/lib/systemd/system目录下创建nacos.service文件 [Unit] Descriptionalibaba nacos Afternetwork.target Documentationhttps://nacos.io/zh-cn/[Service] Userroot Grouproot Typeforking Environment"JAVA_HOME/usr/local/programs/jdk-8u333-li…...

C++核心编程--继承篇
4.6、继承 继承是面向对象三大特征之一 有些类与类之间存在特殊的关系,例如下图中: 我们发现,定义这些类的定义时,都拥有上一级的一些共性,还有一些自己的特性。那么我们遇到重复的东西时,就可以考虑使…...

小程序 解决自定义弹窗滚动穿透问题,解决弹窗背景内容滚动问题
方法一、catchtouchmove"true", 可以实现弹框背景不滚动,但是也会导致弹框自身无法滚动,如果你的弹窗本身是不需要滚动的,用这个方法是极佳的。 <view class"pop" catchtouchmove"true"> …...
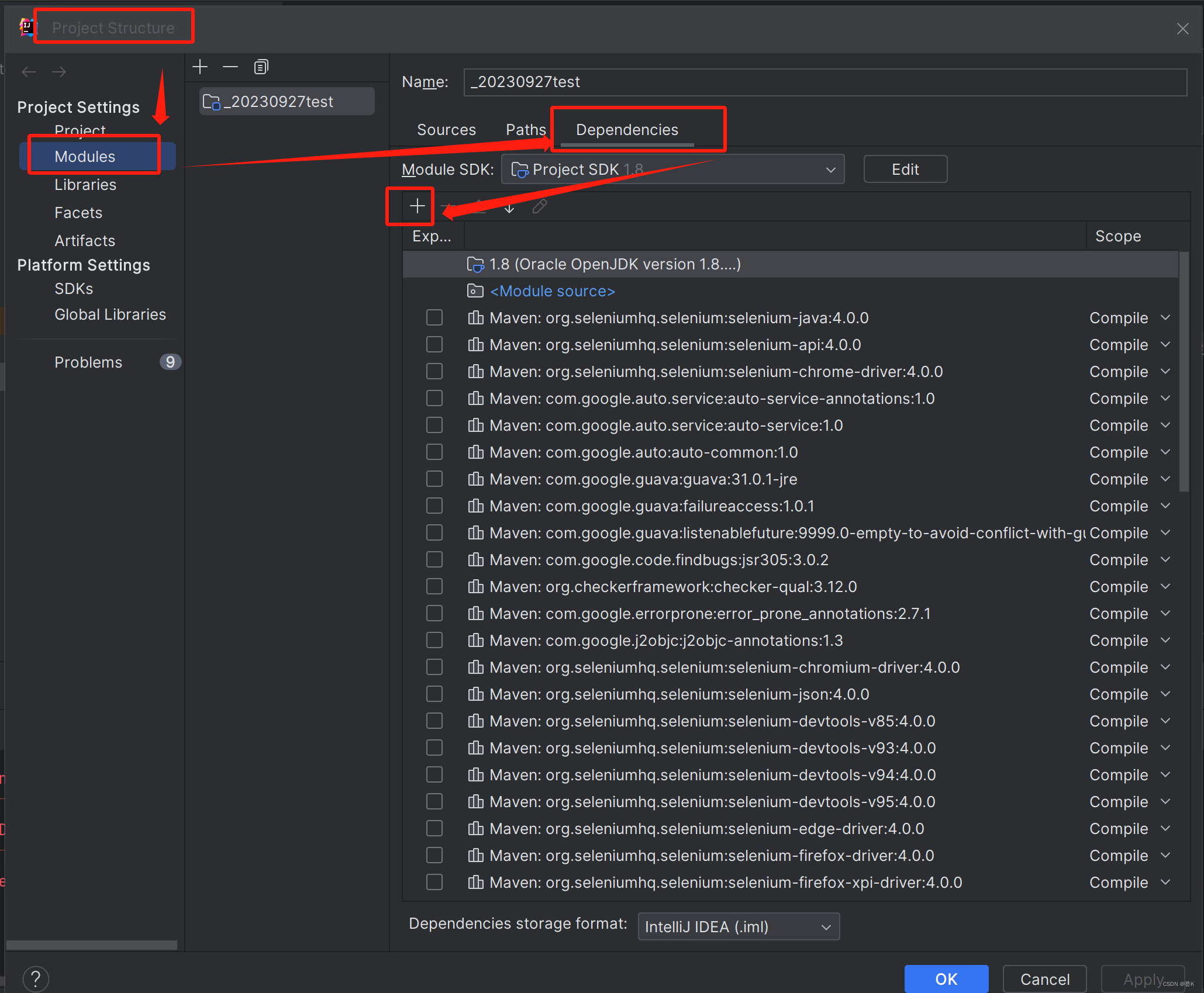
win10搭建Selenium环境+java+IDEA(2)
接着上一个搭建环境开始叙述:win10系统x64安装java环境以及搭建自动化测试环境_荟K的博客-CSDN博客 上一步结尾的浏览器驱动,本人后面改到了谷歌浏览器.exe文件夹下: 这里需要注意,这个新路径要加载到系统环境变量中。 上一步下…...

抢先一步感受未来:Raspberry Pi 5正式发布!
在经历了几年全球供应链困境导致 Raspberry Pi 单板计算机的产能降低和零售价格上涨之后,今天终于迎来了更新。Raspberry Pi 4 上市四年后,今天Raspberry Pi 5正式发布!新推出的 Raspberry Pi 5 配备了经过大幅改进升级的SoC,带来…...

【教程】Ubuntu自动查看有哪些用户名与密码相同的账户,并统一修改密码
转载请注明出处:小锋学长生活大爆炸[xfxuezhagn.cn] 目录 背景说明 开始操作 修改密码 背景说明 有些用户为了图方便或者初始创建用户默认设置等原因,会将密码设置为与用户名相同,但这就使得非常不安全。甚至如果该用户具有sudo权限&#…...
基于 Python+DenseNet121 算法模型实现一个图像分类识别系统
项目展示 一、介绍 DenseNet(Densely Connected Convolutional Networks)是一种卷积神经网络(CNN)架构,2017年由Gao Huang等人提出。该网络的核心思想是密集连接,即每一层都接收其前面所有层的输出作为输…...

贪心算法-点灯问题
1、题目描述 给定一个字符串str,只由 ‘X’ 和 ‘.’ 两种字符构成。‘X’ 表示墙,不能放灯,点亮不点亮都可;’.’ 表示居民点,可以放灯,需要点亮。如果灯放在i位置,可以让 i-1,i 和…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
