【C++数据结构】二叉树搜索树【完整版】

目录
一、二叉搜索树的定义
二、二叉搜索树的实现:
1、树节点的创建--BSTreeNode
2、二叉搜索树的基本框架--BSTree
3、插入节点--Insert
4、中序遍历--InOrder
5、 查找--Find
6、 删除--erase
完整代码:
三、二叉搜索树的应用
1、key的模型 :判断在不在
2、key/value的模型:通过key找value
key/value的应用场景
应用场景1--中英文互译
应用场景2--统计水果出现次数
四、二叉搜索树性能分析
一、二叉搜索树的定义
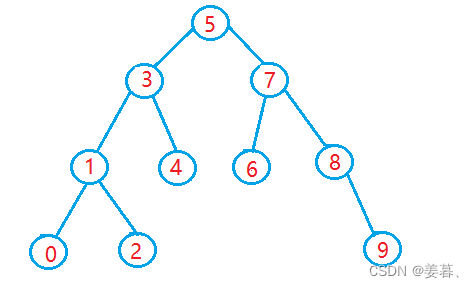
二叉搜索树(也称为搜索二叉树)又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
二、二叉搜索树的实现:
这里最好不用递归,递归比非递归更复杂,故用非递归实现
分两个文件:
BSTree.hpp(因为要用模板实现,而模板的实现和声明要放在一起的,若用模板实现就可用.hpp为后缀和 Test.c
1、树节点的创建--BSTreeNode
树是由节点组成的,故应写个BSTreeNode用来表示每个树节点,_left表示左指针,_right表示右指针,还有一个位置用来存值_key,因为无法确定存的是什么类型的值,故用模板来实现通用,设置成struct是因为树的节点对外是公开的,外部都可以访问的
template<class K> struct BSTreeNode {BSTreeNode(const K& key):_key(key), _left(nullptr), _right(nullptr){}BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key; };
2、二叉搜索树的基本框架--BSTree
对于树的成员变量,一个根节点即可
template<class K> class BSTree //Binary Search Tree {typedef BSTreeNode<K> Node; public:private:Node* _root = nullptr;可以直接定义,就一个成员变量,无需写个构造函数 };
3、插入节点--Insert
这个函数需要有返回值的,以bool作为返回类型,因为这棵树中不允许数据冗余,即不能出现相同的数据。
插入就是用性质:左子树的值都比当前根节点的值小,右子树的值都比当前根节点的值大
若插入一个数据key,从根节点(用cur指针来表示当前位置)开始往下比就好了
①、如果key比当前节点的值大,那就接着往右走
②、如果key比当前节点的值小,那就接着往左走
对于①②直到找到一个空位置插入即可
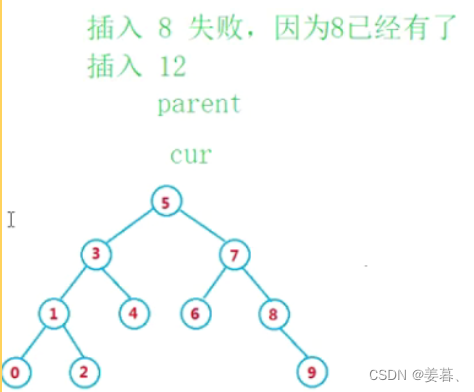
③、如果走的过程中遇到相等的值,说明该key值不能插入,但要注意一个条件,如果这棵树本来就为空,那就直接把数据插入到根节点中就好
链接问题:
插入一个节点,必然要与树链接,若不链接,这个节点就是个临时数据,出了作用域就没了,但若把他链接到树上就能正常访问了,故这里采用双指针法,cur表示当前节点,再定义一个parent,每次cur走之前,先把cur赋值给parent,这样最后cur走到空了,parent能记录到cur的上一位置,而这上一位置就是要找的cur要与其链接的位置,至于cur插入到parent的左还是右,若值比parent的值大,则插到右边,小,则插到左边
bool Insert(const K& key) {if (_root == nullptr){//若为空树,就给它一个节点_root = new Node(key);//new是开空间+初始化,所以要调用构造函数,你要写的return true;}Node* cur = _root;//从根节点开始比较Node* parent = nullptr;while (cur){//都会找一个空位置插入,不会说挪动节点来进行插入if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//若在走的过程中遇到相同的数据,返回假,这个数据无法插入return false;}}cur = new Node(key);//向这个空位置插入数据//利用parent的位置与cur连接if (parent->_key > key)parent->_left = cur;//比根节点小,链接到左边elseparent->_right = cur;//比根节点大,链接到右边return true; }
4、中序遍历--InOrder
这里用两个成员函数实现,为什么?中序遍历你要传树的根节点,而根节点就是类的私有成员变量,而你的中序遍历一定是在类外使用的,无法直接访问_root
解决方法:
法一、写个成员函数获得一下_root是可以的
法二、用两个成员函数,即用InOrder来传这个_root,成员函数访问你_root一定是没问题的,那么_InOrder直接用来中序遍历即可,调用时直接调用InOrder即可
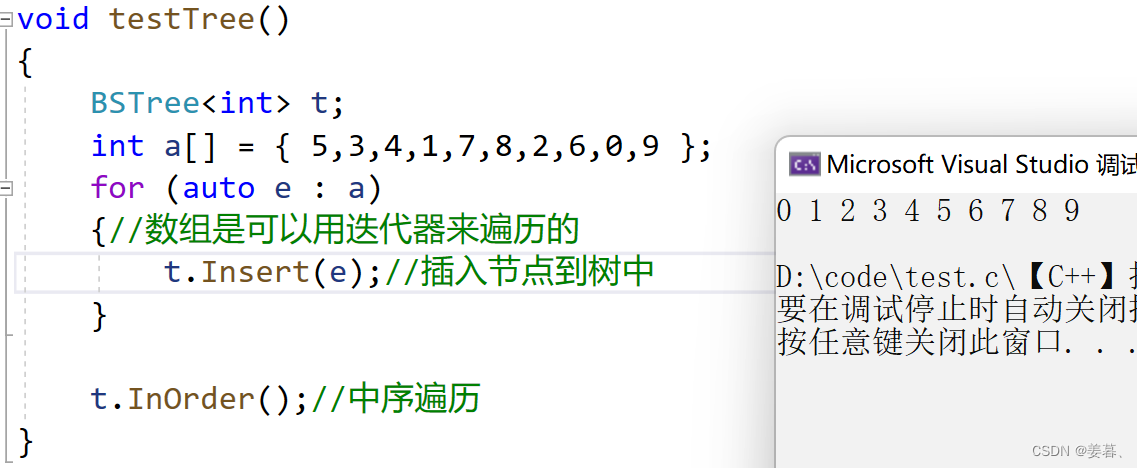
void InOrder() {_InOrder(_root);cout << endl; } //下面的可以放到private里面 void _InOrder(Node* root) {if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right); }下面利用写的插入和中序遍历测试下代码:
void testTree() {BSTree<int> t;int a[] = { 5,3,4,1,7,8,2,6,0,9 };for (auto e : a){//数组是可以用迭代器来遍历的t.Insert(e);//插入节点到树中}t.InOrder();//中序遍历 }
5、 查找--Find
bool Find(const K& key) {Node* cur = _root;while (cur){if (cur->_key > key) {cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return true;//说明相等,则找到了,返回真}}return false;//走到空还没找到,说明没有此数据 }
6、 删除--erase
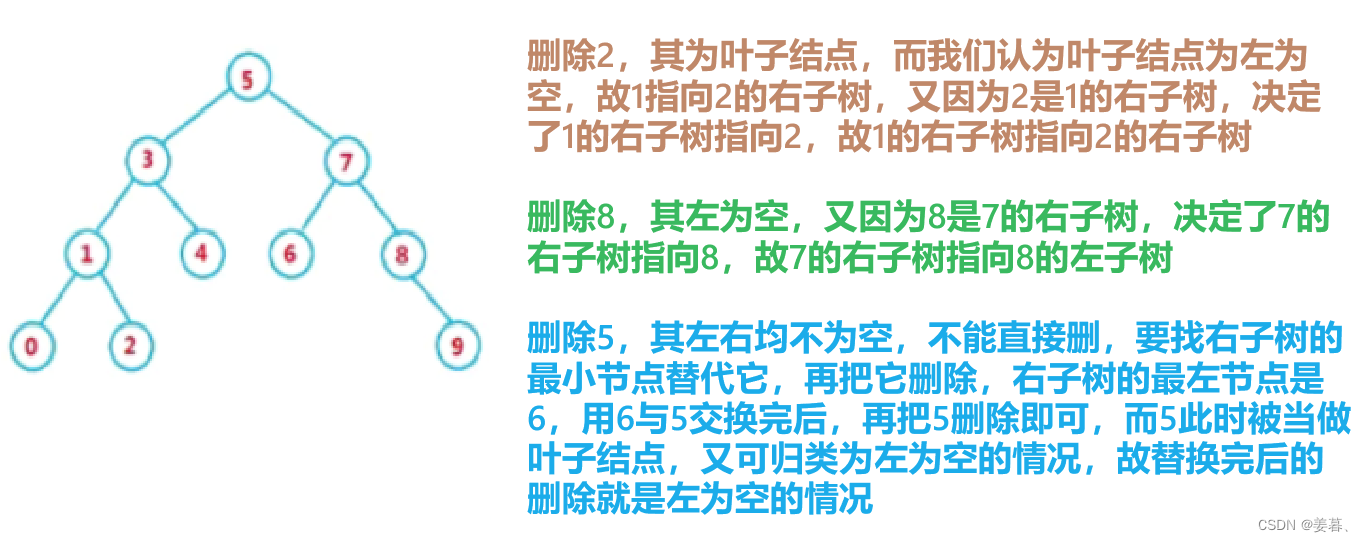
1、观察现象:
删除2,让父亲指向我的右,删除8,让父亲指向我的右,5不好删,因为他有两个孩子
左为空,父亲指向我的右,右为空,父亲指向我的左,叶子节点可以归纳为左为空(右为空也行,这里就假设用左为空),因为叶子的左右都为空,它父亲的指向他的左还是右均可
左为空,
2、细节考虑
A、待删除节点左为空或右为空的情况(叶子结点可归类为左为空)
删除一个节点是让其父亲(Parent)的左指针还是右指针指向cur?
【若cur的左子树为空】看cur到底是父亲的左子树还是右子树,若是父亲的左子树,则让父亲的左指向cur右子树 ,若为右子树,则让父亲的右指向cur的右子树
【若cur的右子树为空】若是父亲的左子树,则让父亲的左指向cur左子树 ,若为右子树,则让父亲的右指向cur的左子树
B、待删除节点左右都不为空的情况
节点的左右子树都不为空,不能直接删除,直接删除会导致二叉搜索树混乱,故用替代法删除。
因为要符合左子树都比根节点小,右子树都比根节点大的性质,故要找左子树的最大节点或右子树的最小节点去替代它。(左子树最右边的节点是左子树最大节点,右子树的最左边的节点是右子树最小节点)【故假设我们下面就用右子树的最小节点】
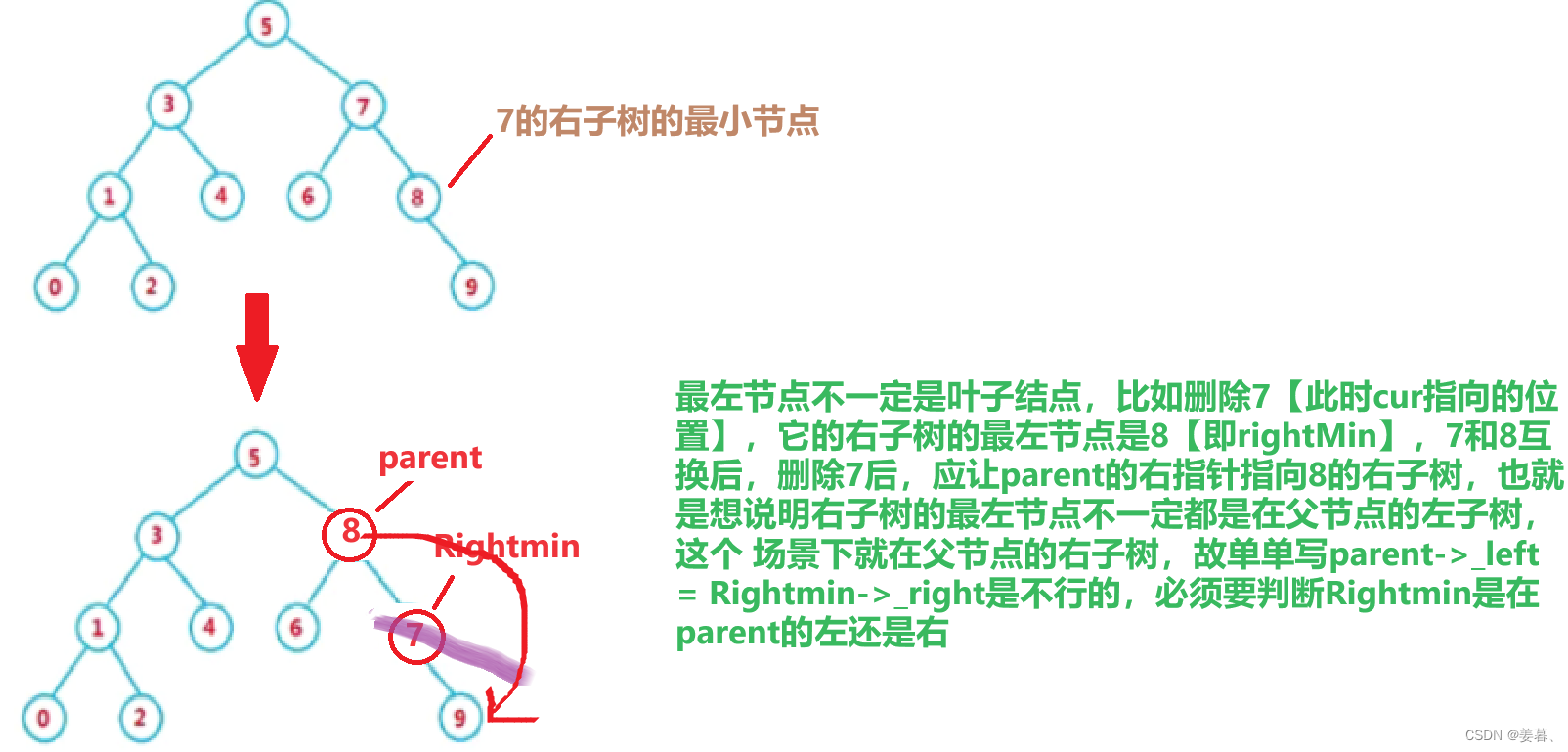
比如删除7,可以用8(7的右子树的最左节点)来替代,那么替换完后,我删除这个7就可以直接删了,那么这个问题又转换到了被删除节点的左为空或者右为空,因为替换节点一定要么是最左边的节点要么是最右边的节点(不一定是叶子结点),那这个替换节点的左右子树一定存在左子树右子树有个为空的情况
所以删除 分三种情况
问题1:
删除一定要找到父亲,因为删完了还存在链接关系,所以单单用find去找是不行的,他找不到他的父亲节点,故还是用双指针法
因为链接问题,所以删除关键看cur是在父亲的左还是右,而不是看cur的左边为空还是右边为空,这不符合所有场景
问题2:
最左节点不一定就是叶子结点,比如这里删除7,它的右子树的最左节点是8,则8替换完7后,8要被删除,他被删除完后,parent的右指针要指向rightMin的右节点
问题3:
parent初始值不能为nullptr,若删除7【che指针指向7】,因为要删除cur,Rightmin刚上来就=8,Rightmin的左子树为空,while循环都没进去,而parent它还是nullptr,那后续的链接肯定会有问题的,所以parent应该一上来就赋值为cur,而不是nullptr
问题4:
若要删除的节点是根节点,也要特别考虑,左为空,则让根=它的右节点,右为空,则让根=它的左节点
bool Erase(const K& key)
{Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//找到了,开始删除//1.左为空if (cur->_left == nullptr){if (cur == _root)_root = cur->_right;else{if (parent->_left == cur)parent->_left = cur->_right;//cur在父亲的左边,就让父亲的左指向cur的左elseparent->_right = cur->_right;//cur在父亲的右边,就让父亲的右指向cur的右}delete cur;}//2.右为空else if (cur->_right == nullptr){if (cur == _root)_root = cur->_left;else{if (parent->_right == cur)parent->_right = cur->_left;//cur在父亲的右边,就让父亲的右指向cur的左elseparent->_left = cur->_left;//cur在父亲的左边,就让父亲的左指向cur的右}delete cur;}//3.左右都不为空else{//找左子树的最右节点或右子树的最小节点去替代//这里用右子树的最小节点来替代Node* parent = cur;Node* Rightmin = cur->_right;//若用右树的最小节点,即右树最左节点while (Rightmin->_left){//最左节点的左子树一定为空,故为判断条件parent = Rightmin;//替换节点不一定是叶子结点,故还要用parent来链接Rightmin = Rightmin->_left;}cur->_key = Rightmin->_key;//用cur的值来替代//转换成删除Rightmin//若它是parent的右子树,则父亲的右指向它的右//若它是parent的左子树,则父亲的左指向它的左if (Rightmin == parent->_left)parent->_left = Rightmin->_right;elseparent->_right = Rightmin->_right;delete Rightmin;}return true;}}return false;//cur都为空了还没找到,则该数据不存在
}完整代码:
BSTree.hpp
#pragma once
#include<iostream>
using namespace std;template<class K>
struct BSTreeNode
{BSTreeNode(const K& key):_key(key), _left(nullptr), _right(nullptr){}BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;};
template<class K>
class BSTree //Binary Search Tree
{typedef BSTreeNode<K> Node;
public:bool Insert(const K& key){if (_root == nullptr){//若为空树,就给它一个节点_root = new Node(key);//new是开空间+初始化,所以要调用构造函数,你要写的return true;}Node* cur = _root;//从根节点开始比较Node* parent = nullptr;while (cur){//都会找一个空位置插入,不会说挪动节点来进行插入if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//若在走的过程中遇到相同的数据,返回假,这个数据无法插入return false;}}cur = new Node(key);//向这个空位置插入数据//利用parent的位置与cur连接if (parent->_key > key)parent->_left = cur;//比根节点小,链接到左边elseparent->_right = cur;//比根节点大,链接到右边return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key) {cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return true;//说明相等,则找到了,返回真}}return false;}bool Erase(const K& key){Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//找到了,开始删除//1.左为空if (cur->_left == nullptr){if (cur == _root)_root = cur->_right;else{if (parent->_left == cur)parent->_left = cur->_right;//cur在父亲的左边,就让父亲的左指向cur的左elseparent->_right = cur->_right;//cur在父亲的右边,就让父亲的右指向cur的右}delete cur;}//2.右为空else if (cur->_right == nullptr){if (cur == _root)_root = cur->_left;else{if (parent->_right == cur)parent->_right = cur->_left;//cur在父亲的右边,就让父亲的右指向cur的左elseparent->_left = cur->_left;//cur在父亲的左边,就让父亲的左指向cur的右}delete cur;}//3.左右都不为空else{//找左子树的最右节点或右子树的最小节点去替代//这里用右子树的最小节点来替代Node* parent = cur;Node* Rightmin = cur->_right;//若用右树的最小节点,即右树最左节点while (Rightmin->_left){//最左节点的左子树一定为空,故为判断条件parent = Rightmin;//替换节点不一定是叶子结点,故还要用parent来链接Rightmin = Rightmin->_left;}cur->_key = Rightmin->_key;//用cur的值来替代//转换成删除Rightmin//若它是parent的右子树,则父亲的右指向它的右//若它是parent的左子树,则父亲的左指向它的左if (Rightmin == parent->_left)parent->_left = Rightmin->_right;elseparent->_right = Rightmin->_right;delete Rightmin;}return true;}}return false;//cur都为空了还没找到,则该数据不存在}void InOrder(){_InOrder(_root);cout << endl;}//下面的可以放到private里面void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root = nullptr;//可以直接定义,就一个成员变量,无需写个构造函数
};void testTree()
{BSTree<int> t;int a[] = { 5,3,4,1,7,8,2,6,0,9 };for (auto e : a){//数组是可以用迭代器来遍历的t.Insert(e);//插入节点到树中}t.InOrder();//中序遍历
}Test.cpp
#include"BSTree.hpp"int main()
{testTree();return 0;
}三、二叉搜索树的应用
搜索树使用场景:
1、key的模型 :判断在不在
比如进入校园要刷校园卡,卡本质里面有芯片,芯片上存储信息,把学校所有学员的信息存到二叉搜索树(因为他的查找效率很高),然后用机器扫描卡,看你卡的信息是否在我的树中,在就让你进
2、key/value的模型:通过key找value
①、高铁刷身份证
买了票就能进站,刷身份证读的是身份证号码,【key就是身份证,value就是票的信息】然后通过身份证到后台服务器查是否有票的信息,是否是这个车站,这个车次等等,即通过身份证找value
②、中英文互译
中文就是key,英文就是value,即通过中文找英文或通过英文找中文。
③、统计次数
统计次数,即通过一个值找另一个值,用搜索树实现的原因是二叉搜索树的效率高,搜索快
key/value模型的实现只需在我们实现的二叉搜索树中改动一下代码即可,即节点里面除了有key,还有value,但是比较大小的过程还是用key来比较,和value没关系,找到了key就相当于找到了value,因为两者在同一节点中,还要修改的就是Find函数,返回值变成返回节点的指针而不是bool值,因为这样返回的节点既有key又有value
注意:
对于搜索树的修改,搜索树中key是不允许修改的
如果是kv模型的搜索树,可以修改value,但不能修改key,就是因为你改了key就不一定满足二叉搜索树的条件了
kv模型的完整代码:
BSTree.hpp :
//key/value模型
#include<iostream>
#include<string>
using namespace std;template<class K, class V>
struct BSTreeNode
{BSTreeNode(const K& key,const V& value):_key(key),_value(value), _left(nullptr), _right(nullptr){}BSTreeNode<K,V>* _left;BSTreeNode<K,V>* _right;K _key;V _value;};
template<class K, class V>
class BSTree //Binary Search Tree
{typedef BSTreeNode<K,V> Node;
public:bool Insert(const K& key, const V& value){if (_root == nullptr){//若为空树,就给它一个节点_root = new Node(key, value);//new是开空间+初始化,所以要调用构造函数,你要写的return true;}Node* cur = _root;//从根节点开始比较Node* parent = nullptr;while (cur){//都会找一个空位置插入,不会说挪动节点来进行插入if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//若在走的过程中遇到相同的数据,返回假,这个数据无法插入return false;}}cur = new Node(key,value);//向这个空位置插入数据//利用parent的位置与cur连接if (parent->_key > key)parent->_left = cur;//比根节点小,链接到左边elseparent->_right = cur;//比根节点大,链接到右边return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return cur;//说明相等,则找到了,返回真}}return nullptr;}bool Erase(const K& key){Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//找到了,开始删除//1.左为空if (cur->_left == nullptr){if (cur == _root)_root = cur->_right;else{if (parent->_left == cur)parent->_left = cur->_right;//cur在父亲的左边,就让父亲的左指向cur的左elseparent->_right = cur->_right;//cur在父亲的右边,就让父亲的右指向cur的右}delete cur;}//2.右为空else if (cur->_right == nullptr){if (cur == _root)_root = cur->_left;else{if (parent->_right == cur)parent->_right = cur->_left;//cur在父亲的右边,就让父亲的右指向cur的左elseparent->_left = cur->_left;//cur在父亲的左边,就让父亲的左指向cur的右}delete cur;}//3.左右都不为空else{//找左子树的最右节点或右子树的最小节点去替代//这里用右子树的最小节点来替代Node* parent = cur;Node* Rightmin = cur->_right;//若用右树的最小节点,即右树最左节点while (Rightmin->_left){//最左节点的左子树一定为空,故为判断条件parent = Rightmin;//替换节点不一定是叶子结点,故还要用parent来链接Rightmin = Rightmin->_left;}cur->_key = Rightmin->_key;//用cur的值来替代//转换成删除Rightmin//若它是parent的右子树,则父亲的右指向它的右//若它是parent的左子树,则父亲的左指向它的左if (Rightmin == parent->_left)parent->_left = Rightmin->_right;elseparent->_right = Rightmin->_right;delete Rightmin;}return true;}}return false;//cur都为空了还没找到,则该数据不存在}void InOrder(){_InOrder(_root);cout << endl;}//下面的可以放到private里面void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ":" <<root->_value << endl;_InOrder(root->_right);}private:Node* _root = nullptr;//可以直接定义,就一个成员变量,无需写个构造函数
};void testTree1()
{BSTree<string, string>dict;//字典dict.Insert("sort", "排序");dict.Insert("polynomial", "多项式");dict.Insert("femininity", "女性");string str;while (cin >> str){BSTreeNode<string, string>* ret = dict.Find(str);if (ret){cout << ret->_value << endl;}else{cout << "无此单词" << endl;}}
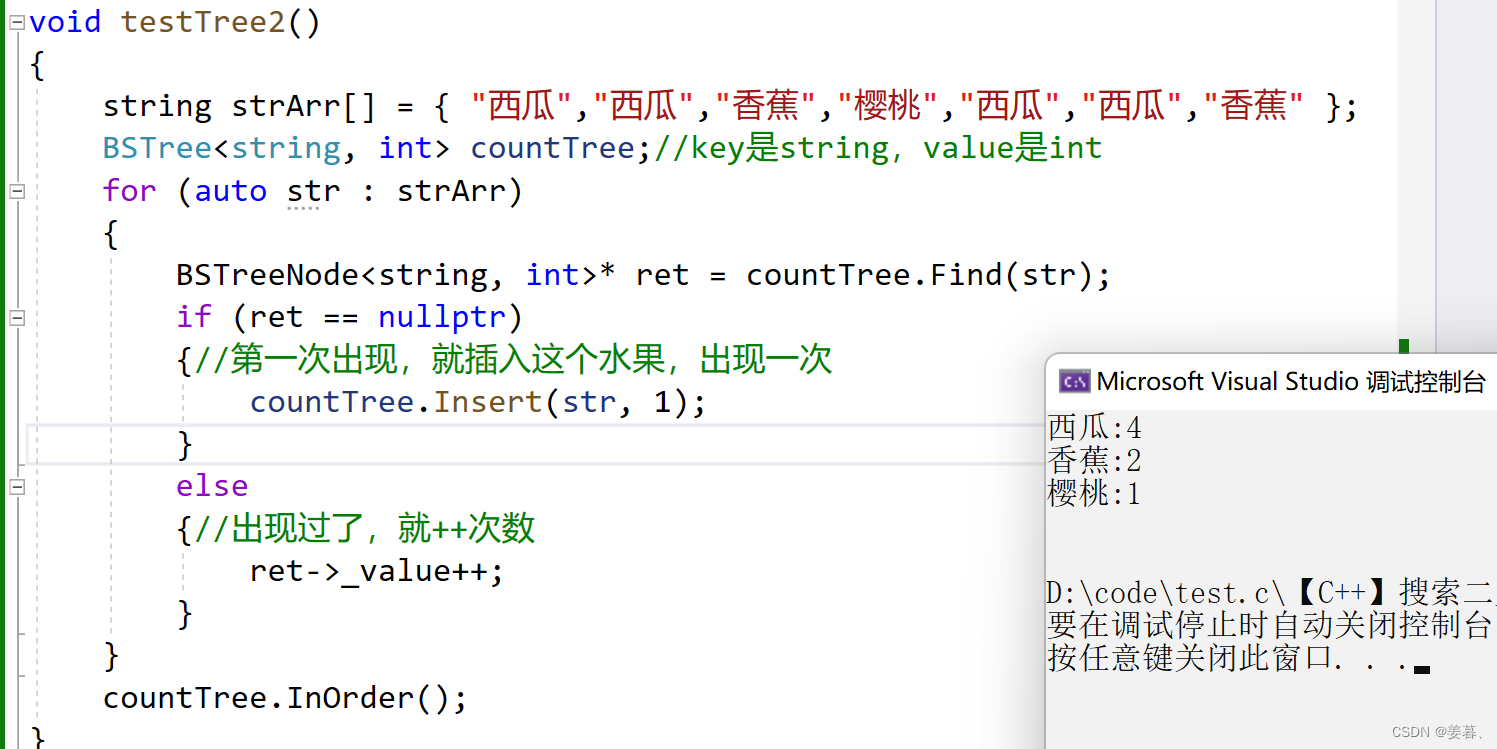
}void testTree2()
{string strArr[] = { "西瓜","西瓜","香蕉","樱桃","西瓜","西瓜","香蕉" };BSTree<string, int> countTree;//key是string,value是intfor (auto str : strArr){BSTreeNode<string, int>* ret = countTree.Find(str);if (ret == nullptr){//第一次出现,就插入这个水果,出现一次,因为一开始树为空countTree.Insert(str, 1);}else{//出现过了,就++次数ret->_value++;}}countTree.InOrder();
}Test.cpp
#include"BSTree.hpp"int main()
{//testTree1();testTree2();return 0;
}key/value的应用场景
应用场景1--中英文互译
key/value模型测试下面代码逻辑(中英文互译)


应用场景2--统计水果出现次数
有一堆水果,请你统计水果出现的次数
四、二叉搜索树性能分析
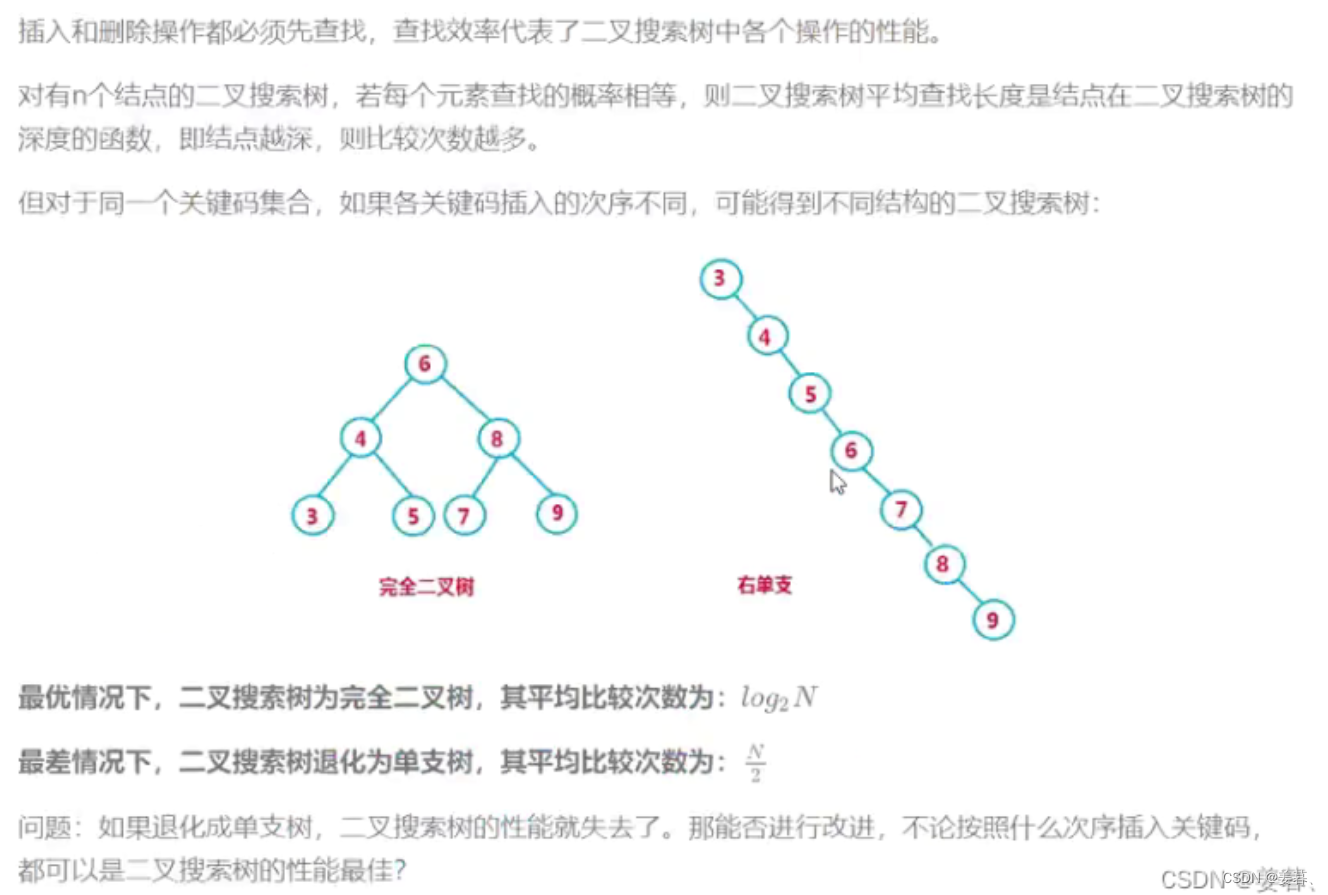
如果插入的数据是有序的或者接近有序的,那么搜索树效率就完全没办法保障
如:1 2 3 4 5 6 7 8,对于树就变成了单支树,搜索树的效率最坏的情况下是O(N)
如何解决?平衡树1、AVLTree 2、红黑树
相关文章:
【C++数据结构】二叉树搜索树【完整版】
目录 一、二叉搜索树的定义 二、二叉搜索树的实现: 1、树节点的创建--BSTreeNode 2、二叉搜索树的基本框架--BSTree 3、插入节点--Insert 4、中序遍历--InOrder 5、 查找--Find 6、 删除--erase 完整代码: 三、二叉搜索树的应用 1、key的模型 &a…...

TouchGFX之字体缓存
使用二进制字体需要将整个字体加载到存储器。 在某些情况下,如果字体很大,如大字号中文字体,则这样做可能不可取。 字体缓存使应用能够从外部存储器只能加载显示字符串所需的字母。 这意味着整个字体无需保存到在可寻址闪存或RAM上ÿ…...
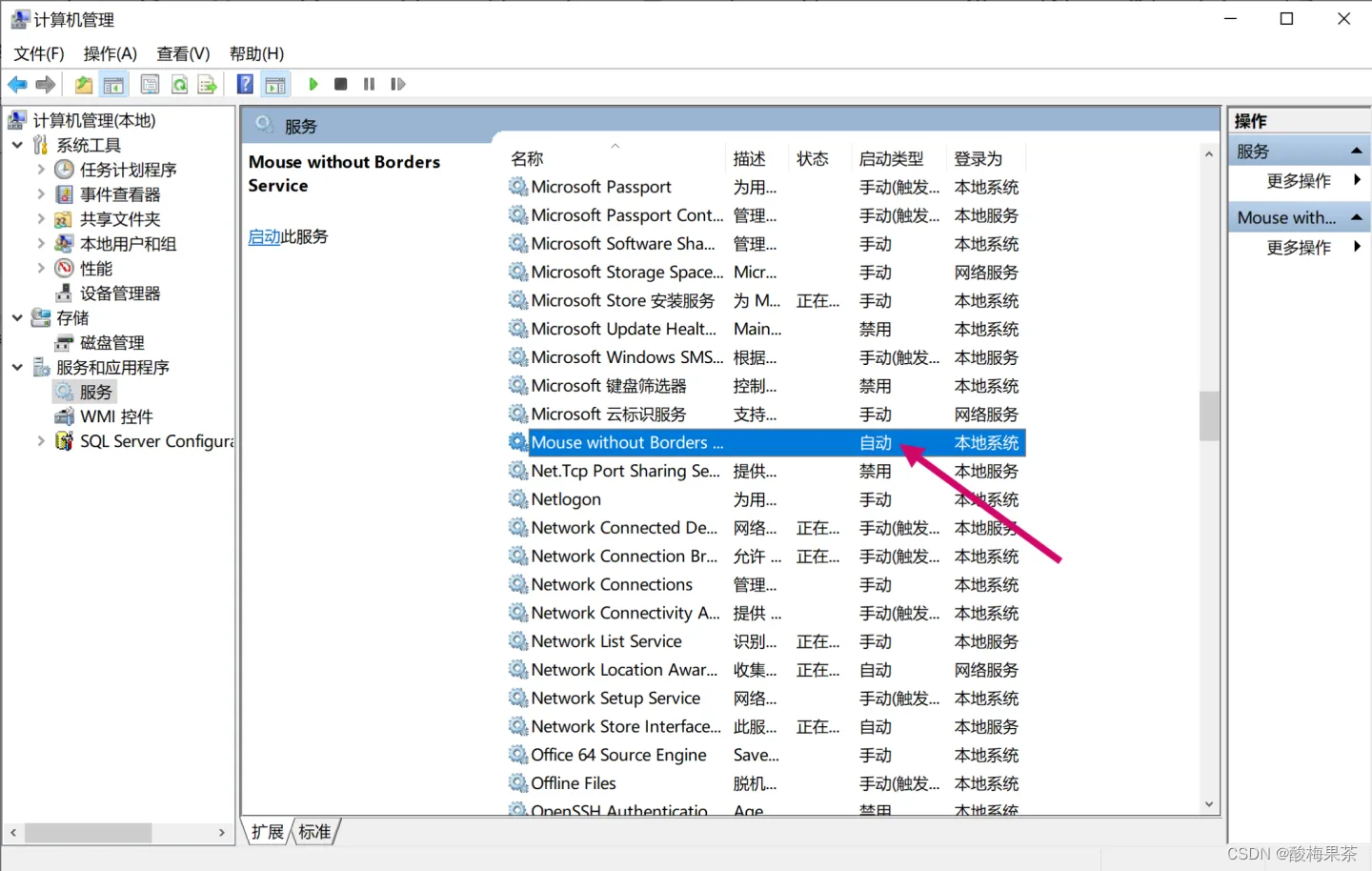
windows系统关闭软件开机自启的常用两种方法
win10中安装软件时经常会默认开机自启动,本文主要介绍两种关闭软件开机自启动方法。 方法1 通过任务管理器设置 1.在任务管理器中禁用开机自启动:打开任务管理器,右键已启动的软件,选择禁用。 方法2 通过windows服务控制开机自启…...
巧用@Conditional注解根据配置文件注入不同的bean对象
项目中使用了mq,kafka两种消息队列进行发送数据,为了避免硬编码,在项目中通过不同的配置文件自动识别具体消息队列策略。这里整理两种实施方案,仅供参考! 方案一:创建一个工具类,然后根据配置文…...
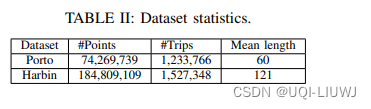
论文笔记(整理):轨迹相似度顶会论文中使用的数据集
0 汇总 数据类型数据名称数据处理出租车数据波尔图 原始数据:2013年7月到2014年6月,170万条数据 ICDE 2023 Contrastive Trajectory Similarity Learning with Dual-Feature Attention 过滤位于城市(或国家)区域之外的轨迹 过…...

Python实现单例模式
使用函数装饰器 def singleton(cls):_instance {}def inner():if cls not in _instance:_instance[cls] cls()return _instance[cls]return innersingleton class Demo(object):def __init__(self):passdef test():b1 Demo()b2 Demo()print(b1, b2)使用类装饰器 class si…...

spark相关网站
Spark的五种JOIN策略解析 https://www.cnblogs.com/jmx-bigdata/p/14021183.html 万字详解整个数据仓库建设体系(好文值得收藏) https://mp.weixin.qq.com/s?__bizMzg2MzU2MDYzOA&mid2247484692&idx1&snf624672e62ba6cd4cc69bdb6db28756a&…...
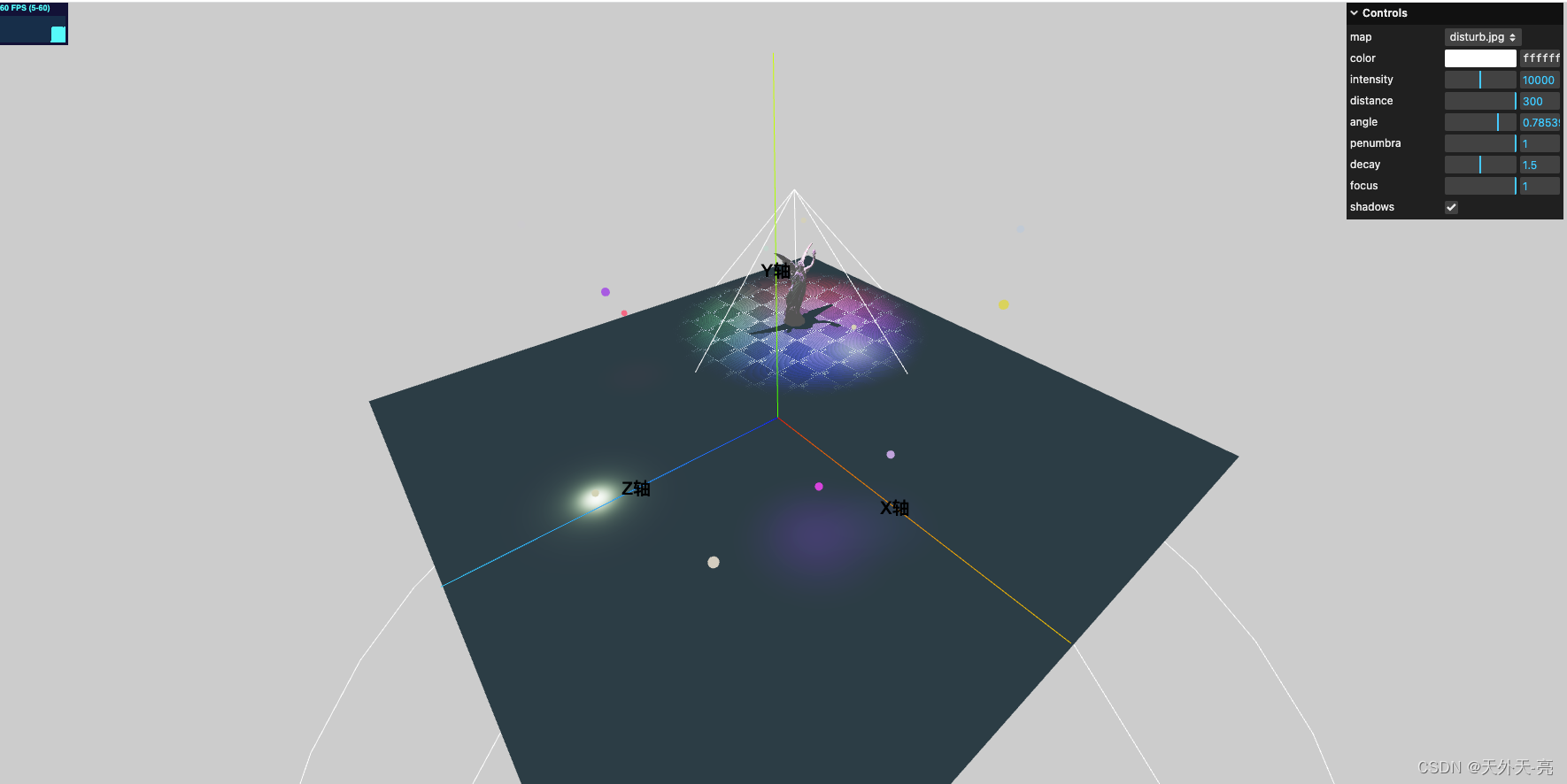
ThreeJS-3D教学四-光源
three模拟的真实3D环境,一个非常炫酷的功能便是对光源的操控,之前教学一中已经简单的描述了多种光源,这次咱们就详细的讲下一些最常见的光源: AmbientLight 该灯光在全局范围内平等地照亮场景中的所有对象。 该灯光不能用于投射阴…...

Linux 回收内存到底怎么计算anon/file回收比例,只是swappiness这么简单?
概述 Linux内核为了区分冷热内存,将page以链表的形式保存,主要分为5个链表,除去evictable,我们主要关注另外四个链表:active file/inactive file,active anon和inactive anon链表,可以看到这主要分为两类,file和anon page,内存紧张的时候,内核开始从inactive tail定…...

软件测试中的测试工具和自动化测试
1. 测试工具 测试工具也分为不同人员使用的 开发人员:测试框架,编写测试用例;各类线上dump分析工具如windgb;开发时的集成IDE工具如Visual Studio,idea等等 面向不同测试需求的测试工具 软件测试是软件开发生命周期…...
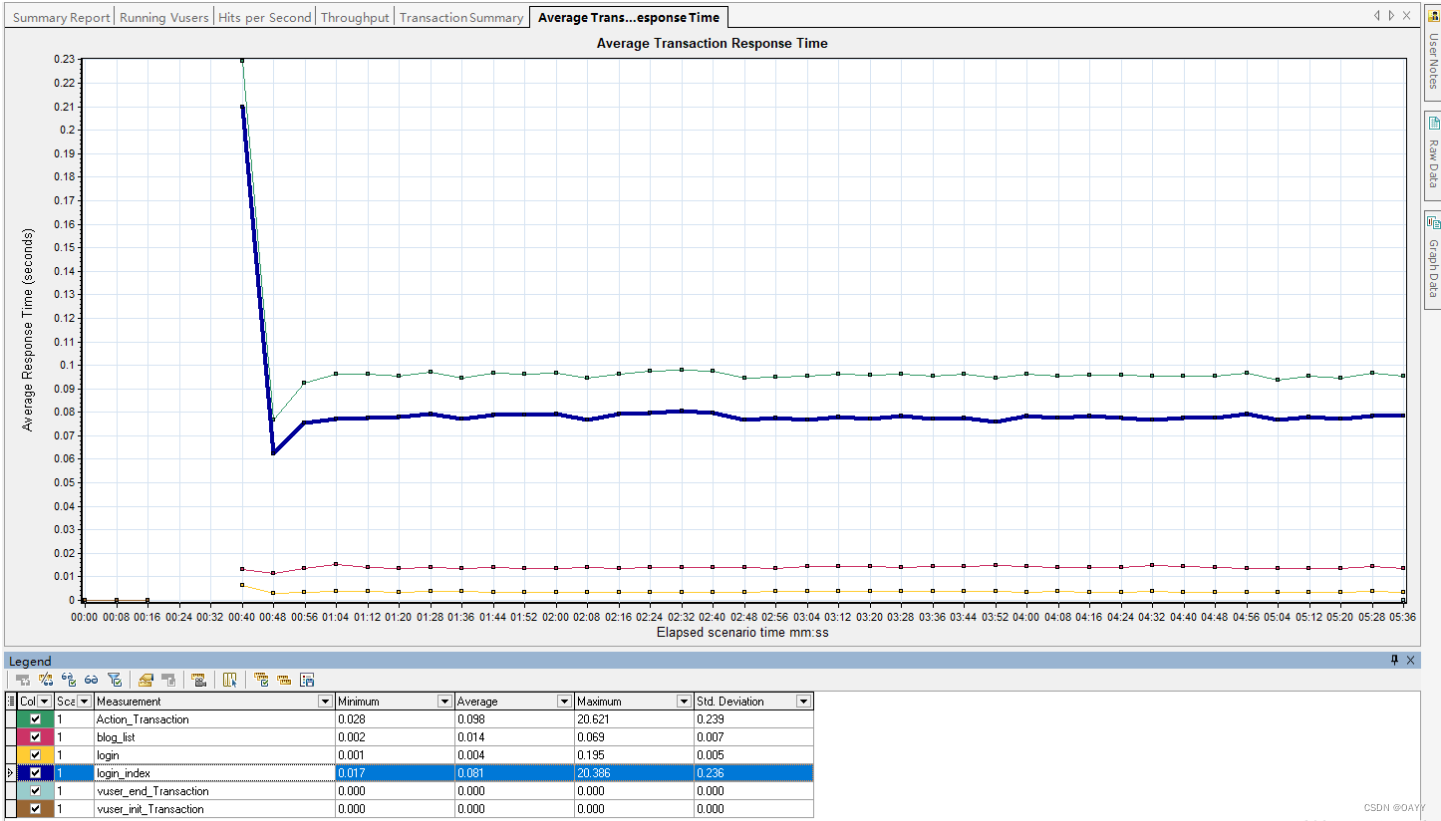
个人博客系统测试报告
个人博客系统测试报告 一.项目背景二.项目功能三.测试用例3.1 功能测试3.2 自动化测试(部分测试)3.2.1登陆页面3.2.2博客详情页3.2.3博客编辑页3.2.4个人列表页3.2.5测试结果 3.3 性能测试 一.项目背景 当学习完一项技能后,我们总会习惯通过博…...
高效搜索,提升编程效率
一、搜索效率 1.1魔法上网 网址: 一个很变态但可以让你快速学会计算机的方法…………_哔哩哔哩_bilibili 谷歌镜像: https://search.fuyeor.com/zh-cn/Google 谷歌学术: https://link.zhihu.com/?targethttps%3A//scholar.lanfanshu.cn/…...
Java编程技巧:文件上传、下载、预览
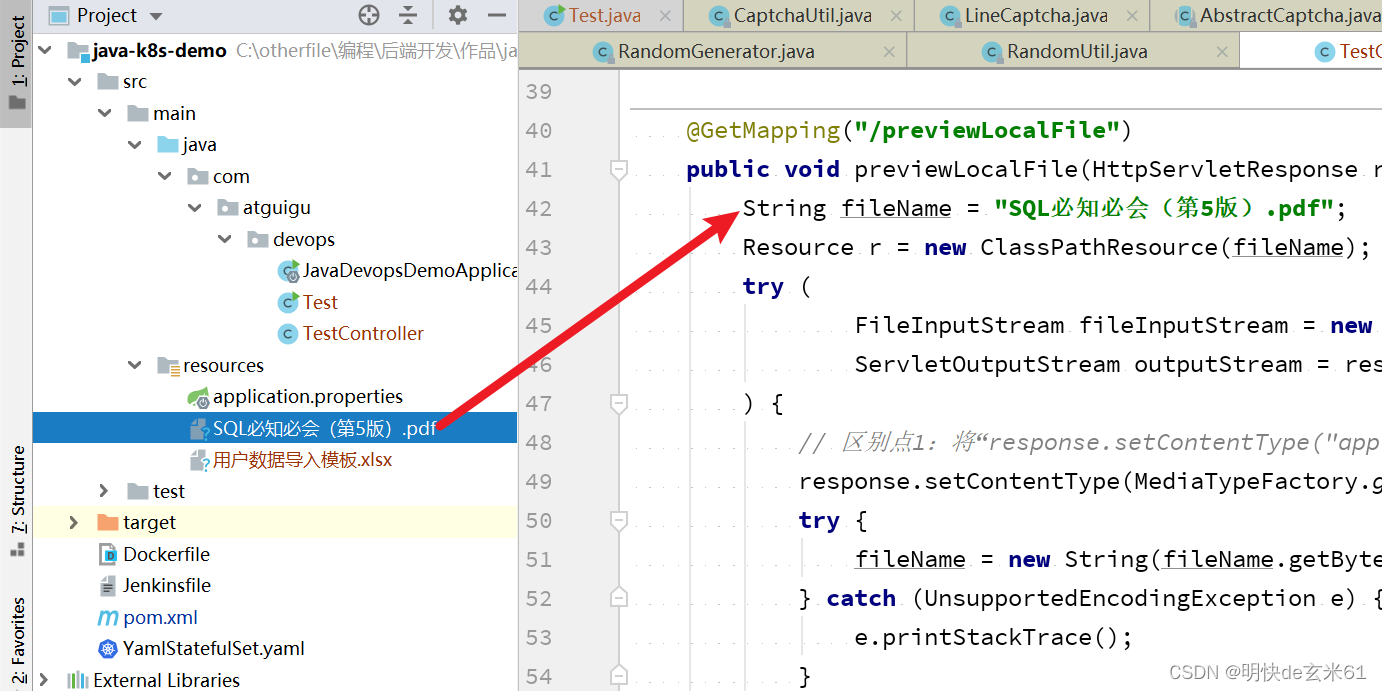
目录 1、上传文件1.1、代码1.2、postman测试截图 2、下载resources目录中的模板文件2.1、项目结构2.2、代码2.3、使用场景 3、预览文件3.1、项目结构3.2、代码3.3、使用场景 1、上传文件 1.1、代码 PostMapping("/uploadFile") public String uploadFile(Multipart…...

【蓝桥杯选拔赛真题63】Scratch云朵降雨 少儿编程scratch图形化编程 蓝桥杯选拔赛真题解析
目录 scratch云朵降雨 一、题目要求 编程实现 二、案例分析 1、角色分析...
【新版】系统架构设计师 - 软件架构的演化与维护
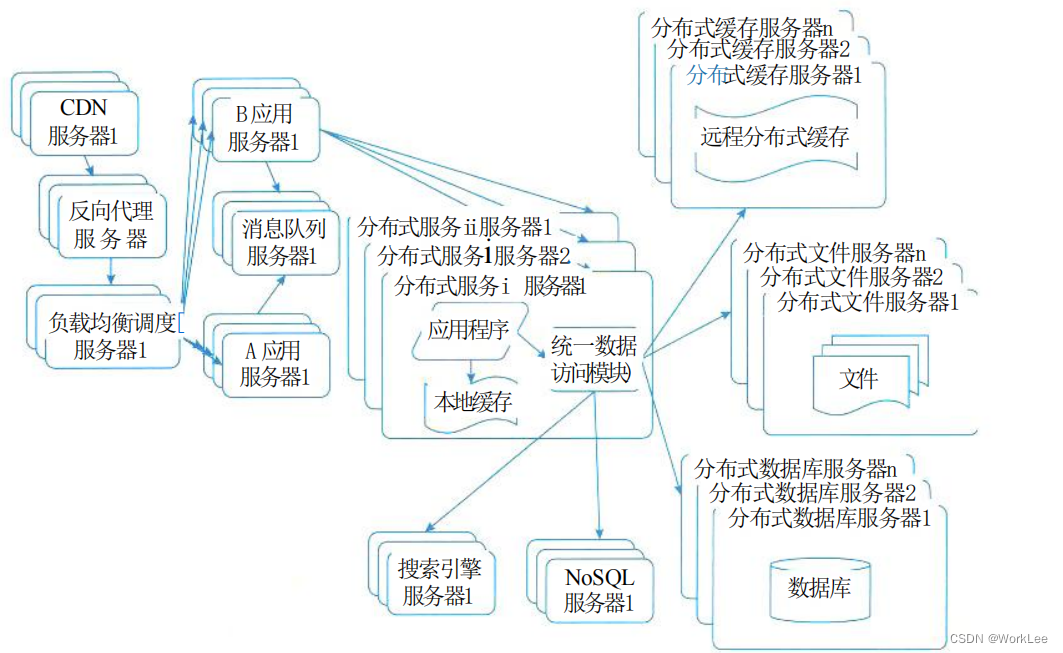
个人总结,仅供参考,欢迎加好友一起讨论 文章目录 架构 - 软件架构的演化与维护考点摘要软件架构演化和定义面向对象软件架构演化对象演化消息演化复合片段演化约束演化 软件架构演化方式静态演化动态演化 软件架构演化原则软件架构演化评估方法大型网站架…...

安卓循环遍历计时器
计时器循环遍历 计时器的使用 我习惯两种方式如下: 第一种使用 handler: 1,初始化 声明 public static final int REGULAR_TIME 1000; //1秒 时间间隔private Handler mUiHandler;private int index0;Runnable runnable new Runnable()…...
Docker-基本了解
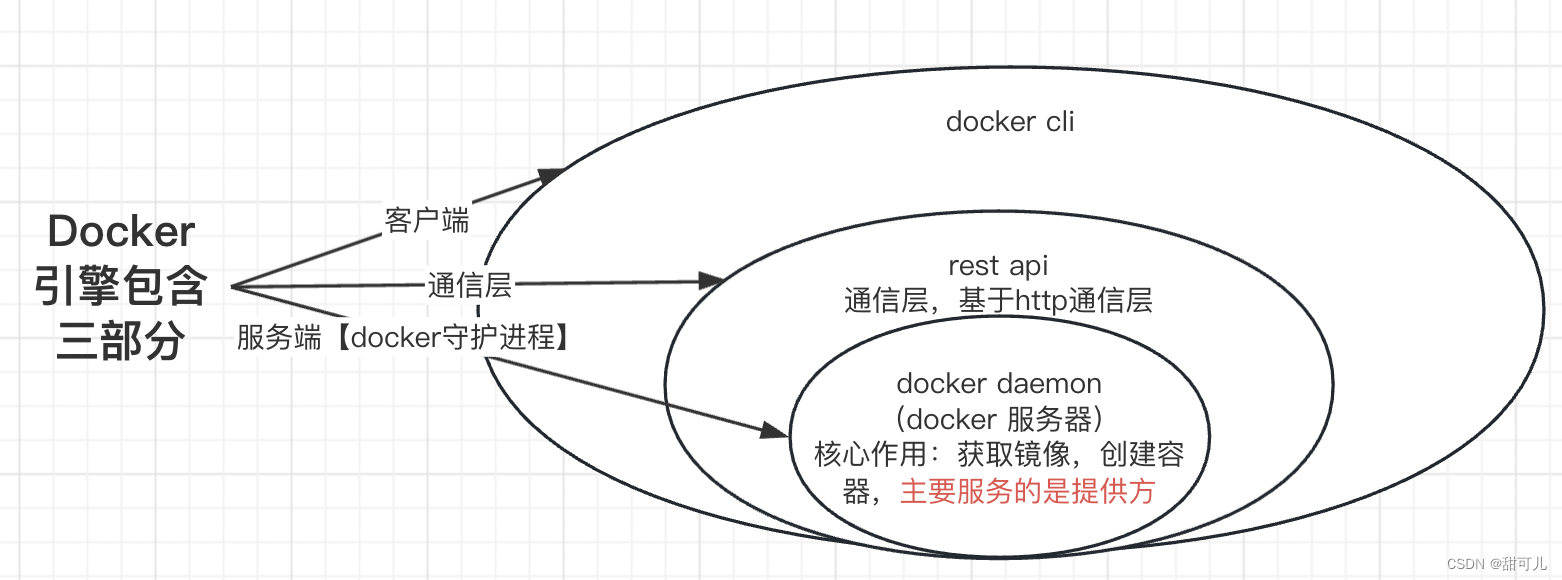
Docker-基本了解 一、基本概念1、镜像2、容器 二、执行流程三、体系结构 一、基本概念 Docker是容器化平台,提供应用打包,部署与运行应用的容器化平台,应用程序通过docker engine(Docker 引擎获取可用资源)࿰…...
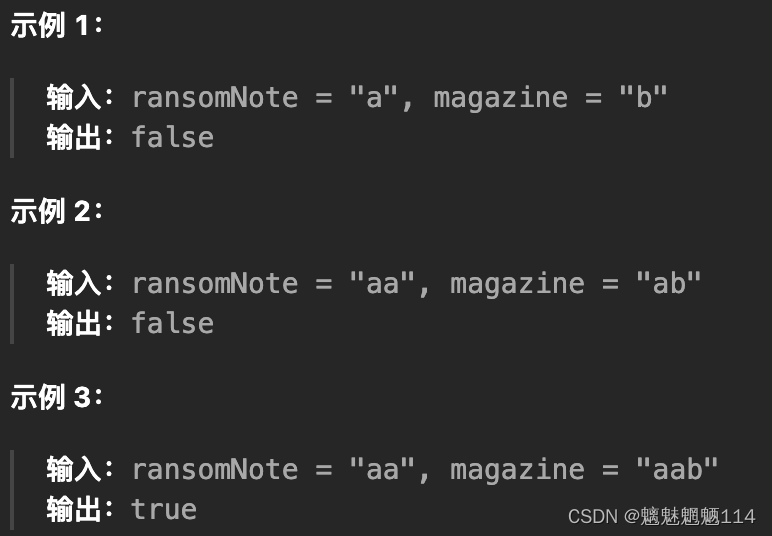
Leetcode383. 赎金信
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。 如果可以,返回 true ;否则返回 false 。 magazine 中的每…...

overleaf杂谈-Springer文献格式问题
目录 overleaf写作问题记录1.Latex中的%问题(文本变成灰色)2.Springer文献格式问题2.1 新建reference.bib2.2 谷歌学术搜索文章并引用2.3 复制BibTex2.4 复制进reference.bib2.5 在sn-article.tex的\end{document}前添加语句2.6 引用文献2.7 Springer模板…...

No148.精选前端面试题,享受每天的挑战和学习
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云课上架的前后端实战课程《Vue.js 和 Egg.js 开发企业级健康管理项目》、《带你从入…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...