Unity如何实现TreeView
前言
最近有一个需求,需要实现一个TreeView的试图显示,开始我一直觉得这么通用的结构,肯定有现成的UI组件或者插件可以使用,结果,找了好久,都没有找到合适的插件,有两个效果差强人意。
最后在回家的路上突然灵光一闪,想到了一种简单的实现方式,什么插件都不用,仅使用Unity自带的Button和Layout。不仅可以实现一级树形目录,还能实现二级,三级等等,只要你有需要,都可以自定义实现。
原理
好了废话不多说,我来说一下原理
我们先来看一下一个基本的TreeView基本结构如下:

我们看左侧的菜单,TreeView有一级标题和二级标题,其中一级标题的点击可以控制二级标题的显示与折叠。
我这里的原理就是给一级标题和二级标题放到一个VerticalLayout父节点V1中,然后我们给V1再添加一个ContentSizeFilter,可以动态控制这组标题的大小。然后多个不同的标题组,我们再用一个大的VerticalLayout控制。
当我们点击一级标题是,就同时控制它同一个父节点下的所有二级子标题的显示与隐藏,当显示这些二级标题节点时,由于ContentSizeFilter的控制,它们的父节点VerticalLayout就会变大尺寸,这样外层Layout就会控制下层的标题组重新刷新位置,树形结构就会正确显示了。
相关文章:

Unity如何实现TreeView
前言 最近有一个需求,需要实现一个TreeView的试图显示,开始我一直觉得这么通用的结构,肯定有现成的UI组件或者插件可以使用,结果,找了好久,都没有找到合适的插件,有两个效果差强人意。 最后在回家的路上突然灵光一闪,想到了一种简单的实现方式,什么插件都不用,仅使用…...

Android widget 小部件使用指南强化版
Android widget 小部件使用指南强化版 一、简单UI的小部件二、含集合的小部件三、可配置的小部件四、可控制的小部件五、Android 12 Widget 更新 小部件是主屏幕定制的一个重要方面。您可以将它们视为应用程序最重要的数据和功能的“概览”视图,这些数据和功能可以直…...
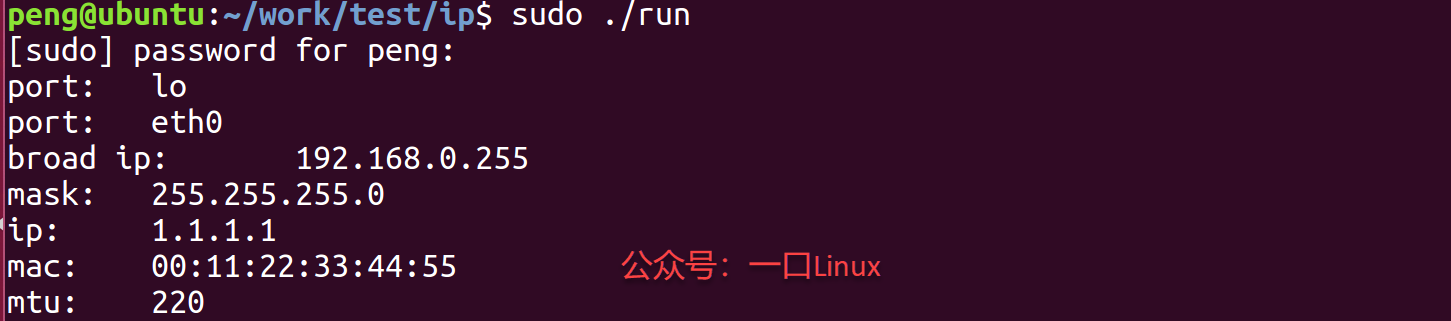
Linux下C语言操作网卡的几个代码实例?特别实用
前面写了一篇关于网络相关的文章:如何获取当前可用网口。 《简简单单教你如何用C语言列举当前所有网口!》 那么如何使用C语言直接操作网口? 比如读写IP地址、读写MAC地址等。 一、原理 主要通过系统用socket()、ioctl()、实现 int sock…...

noip2011选择旅馆
1.审题:第一个人与第二个人入住的旅馆要求是同色的; 两个人去消费的旅馆并没有要求与入住的旅馆是同色的(这点要小心) 2.要求记录以下数据: 1)a[color]表示当前同为颜色color的旅馆数 2)b[co…...
vue造轮子完整指南--npm组件包开发步骤
一、项目包文件的创建和初始化。 1. 新建项目包。 vue create <Project Name> //用于发布npm包的项目文件名 ps:一般选择自定义,然后不需要Vuex和Router,其他选项按自己实际情况选择安装即可。 2.修改原始src文件名、新增组件项目存放文件和修改…...
28 drf-Vue个人向总结-1
文章目录 前后端分离开发展示项目项补充知识开发问题浏览器解决跨域问题 drf 小tips设置资源root目录使用自定义的user表设置资源路径media数据库补充删除表中数据单页面与多页面模式过滤多层自关联后端提交的数据到底是什么jwt token登录设置普通的 token 原理使用流程解析 jw…...

线性代数(七) 矩阵分析
前言 从性线变换我们得出,矩阵和函数是密不可分的。如何用函数的思维来分析矩阵。 矩阵的序列 通过这个定义我们就定义了矩阵序列的收敛性。 研究矩阵序列收敛性的常用方法,是用《常见向量范数和矩阵范数》来研究矩阵序列的极限。 长度是范数的一个特…...
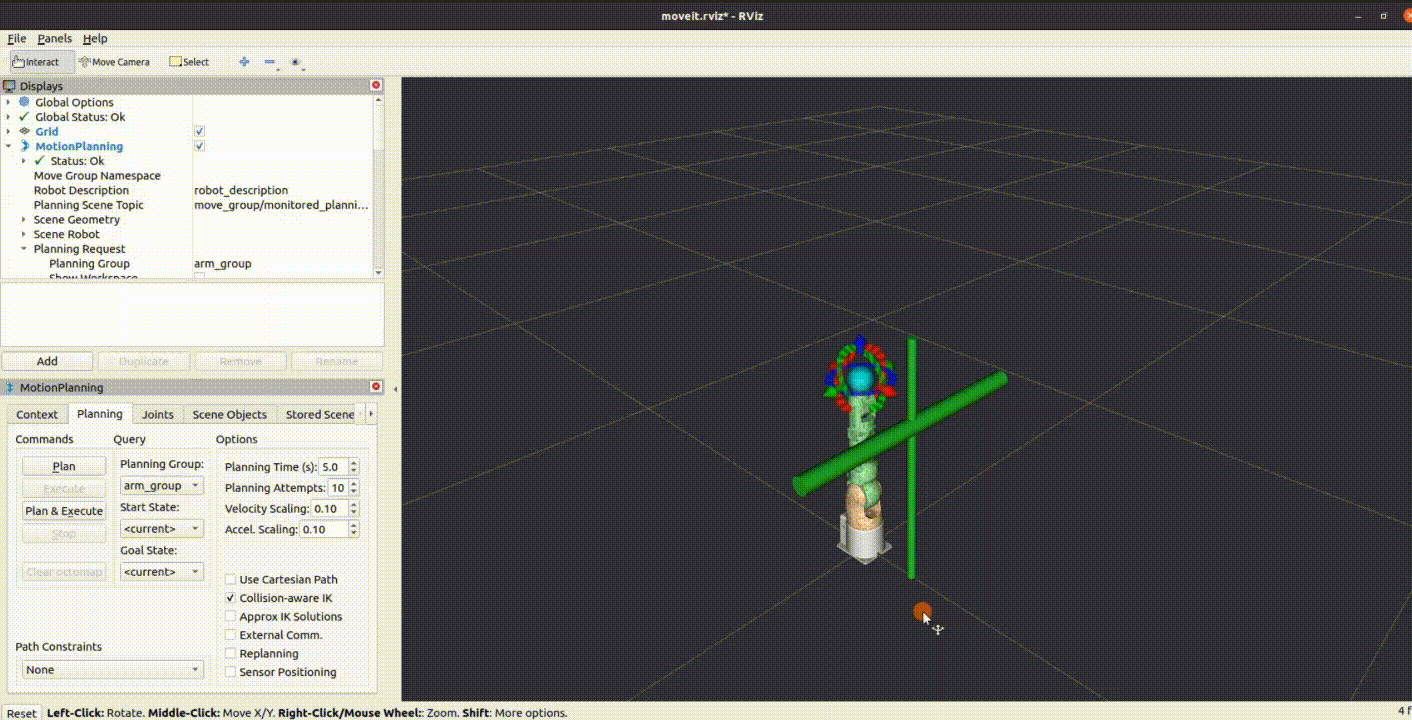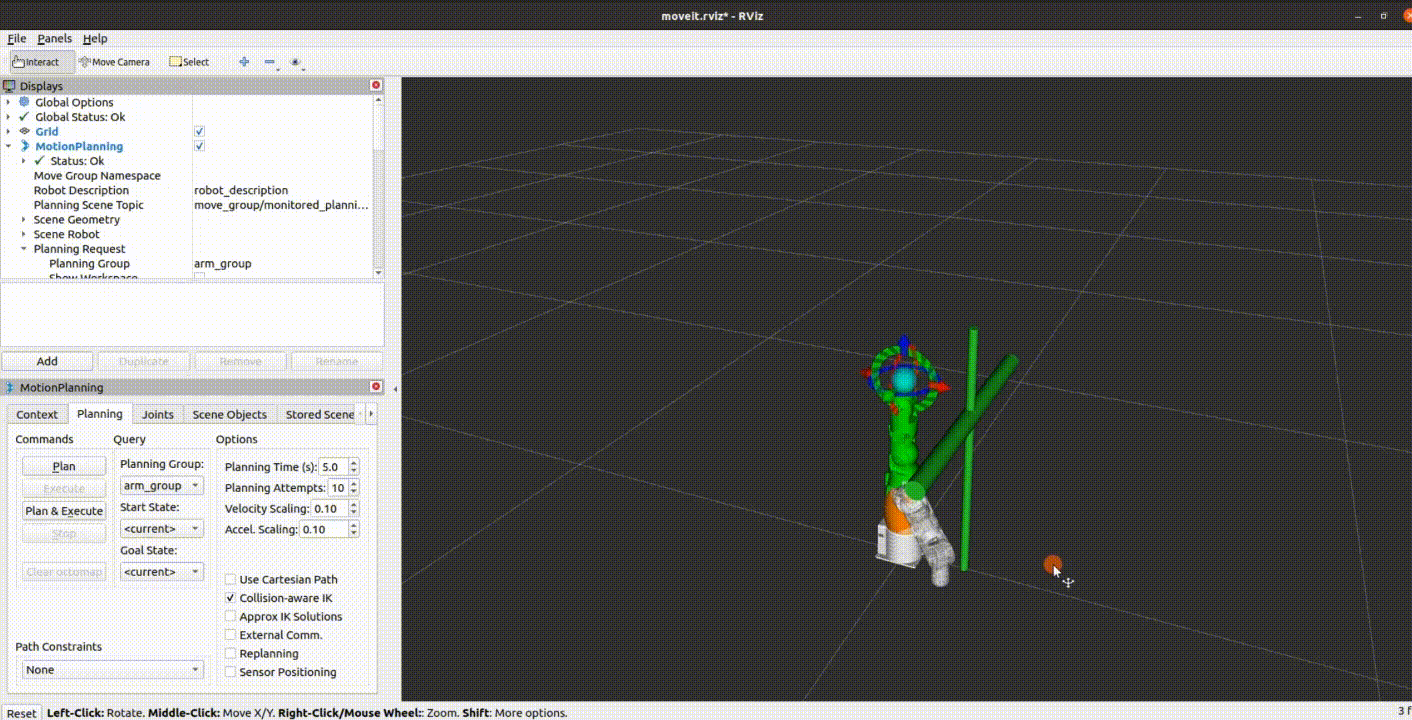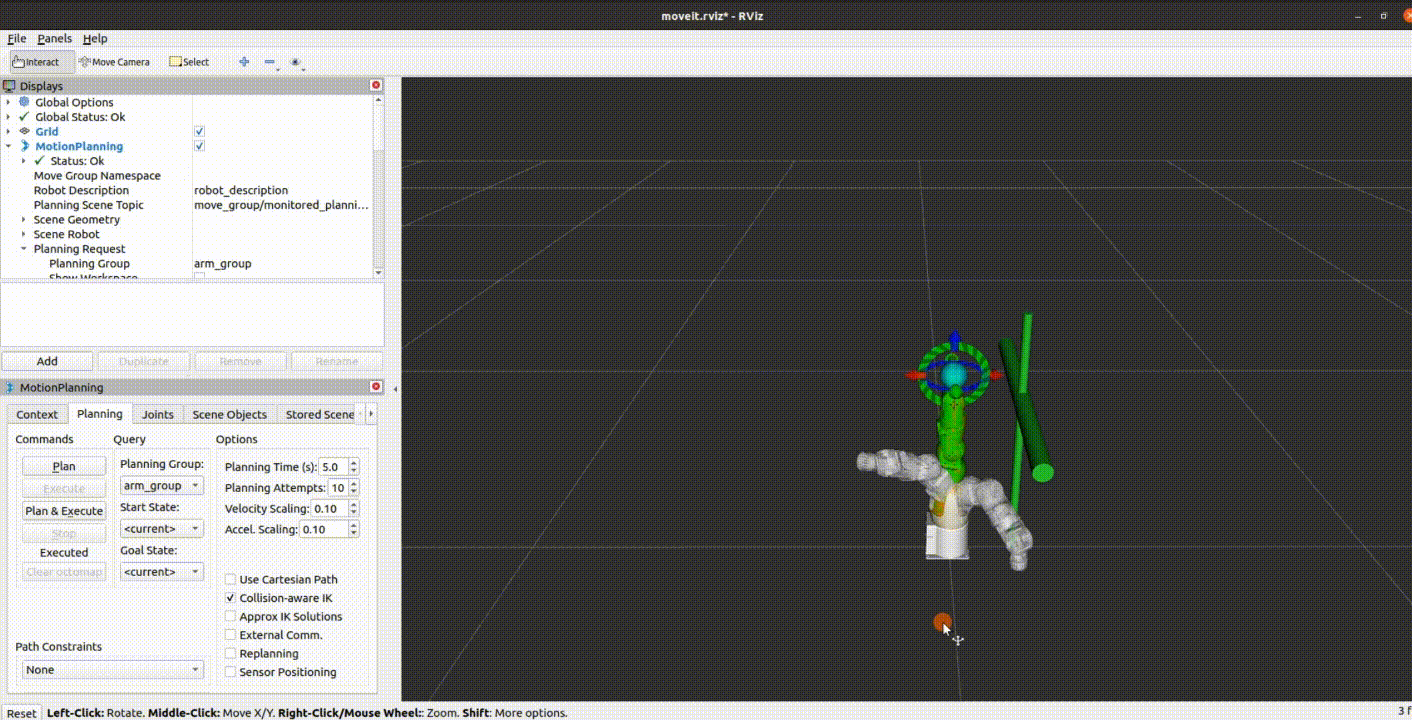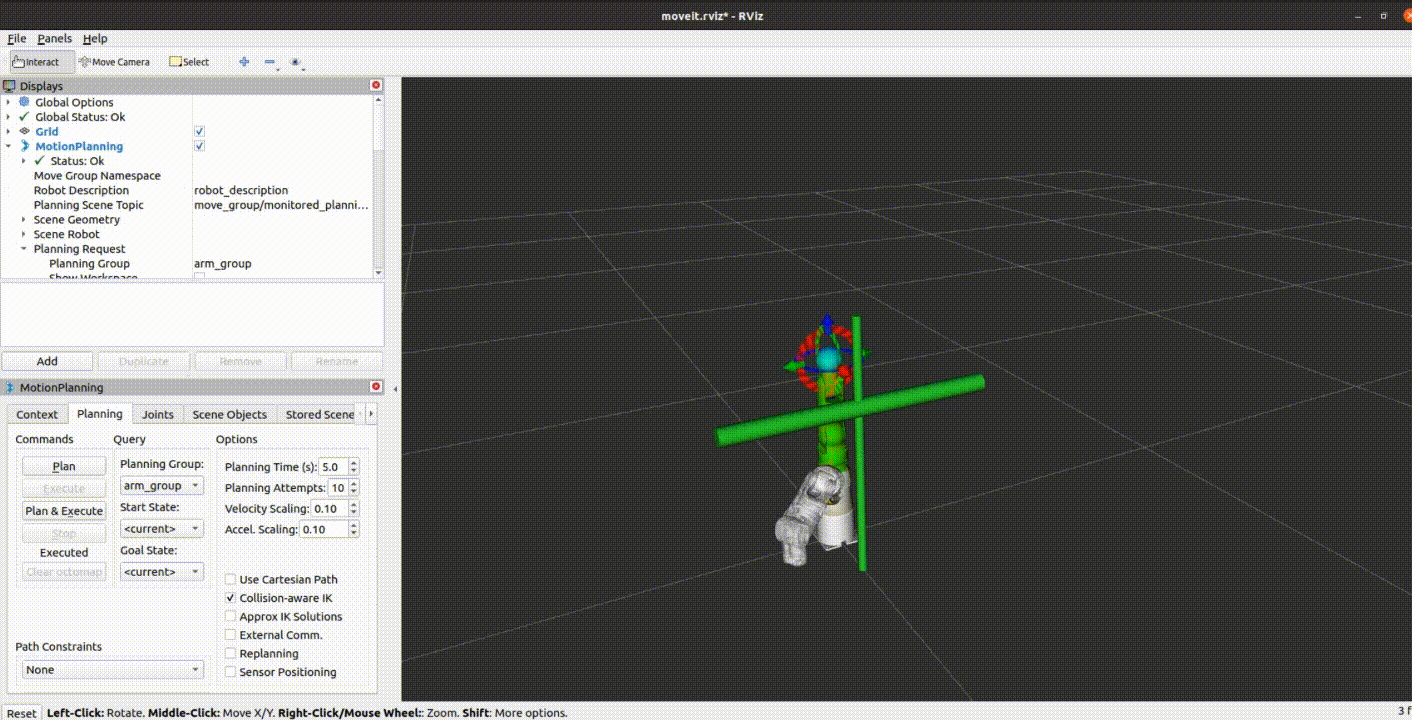
myArm 全新七轴桌面型机械臂
引言 在不断演进的科技世界中,我们始终追求创新和卓越,以满足客户的需求并超越他们的期望。今天,我们很高兴地宣布我们的最新产品——myArm 300 Pi,一款七轴的桌面型机械臂。这款产品的独特之处在于其灵活性和可编程性,…...

tomcat乱码解决
解决乱码 1、修改bin\catalina.bat配置文件 修改tomcat的配置文件,找到tomcat路径下的\bin目录下的catalina.bat文件,修改 set “JAVA_OPTS%JAVA_OPTS% %JSSE_OPTS% -Dfile.encodingUTF-8 -Dsun.jnu.encodingUTF-8 ” 2、修改conf\logging.properties配置…...

【Linux】详解线程第三篇——线程同步和生产消费者模型
线程同步和生消模型 前言正式开始再次用黄牛抢票来讲解线程同步的思想通过条件变量来实现线程同步条件变量接口介绍初始化和销毁pthread_cond_waitsignal和broadcast 生产消费者模型三种关系用基本工程师思维再次理解基于生产消费者模型的阻塞队列版本一版本二多生多消 利用RAI…...

k8s 安装
文章目录 k8s 客户端安装k8s集群minikubekindkubeadm 验证 k8s 客户端 用于连接k8s集群,建议下载1.23.x的版本,其他的版本本地运行可能会有莫名其妙的报错 https://dl.k8s.io/release/v1.23.16/bin/linux/amd64/kubectl 安装k8s集群 minikube Minik…...

红队打靶:THE PLANETS: MERCURY打靶思路详解(vulnhub)
目录 写在开头 第一步:主机发现和端口扫描 第二步:Web渗透 第三步:获取初步立足点并搜集信息 第四步:软连接劫持sudo提权 总结与思考 写在开头 本篇博客在自己的理解之上根据大佬红队笔记的视频进行打靶,详述了…...
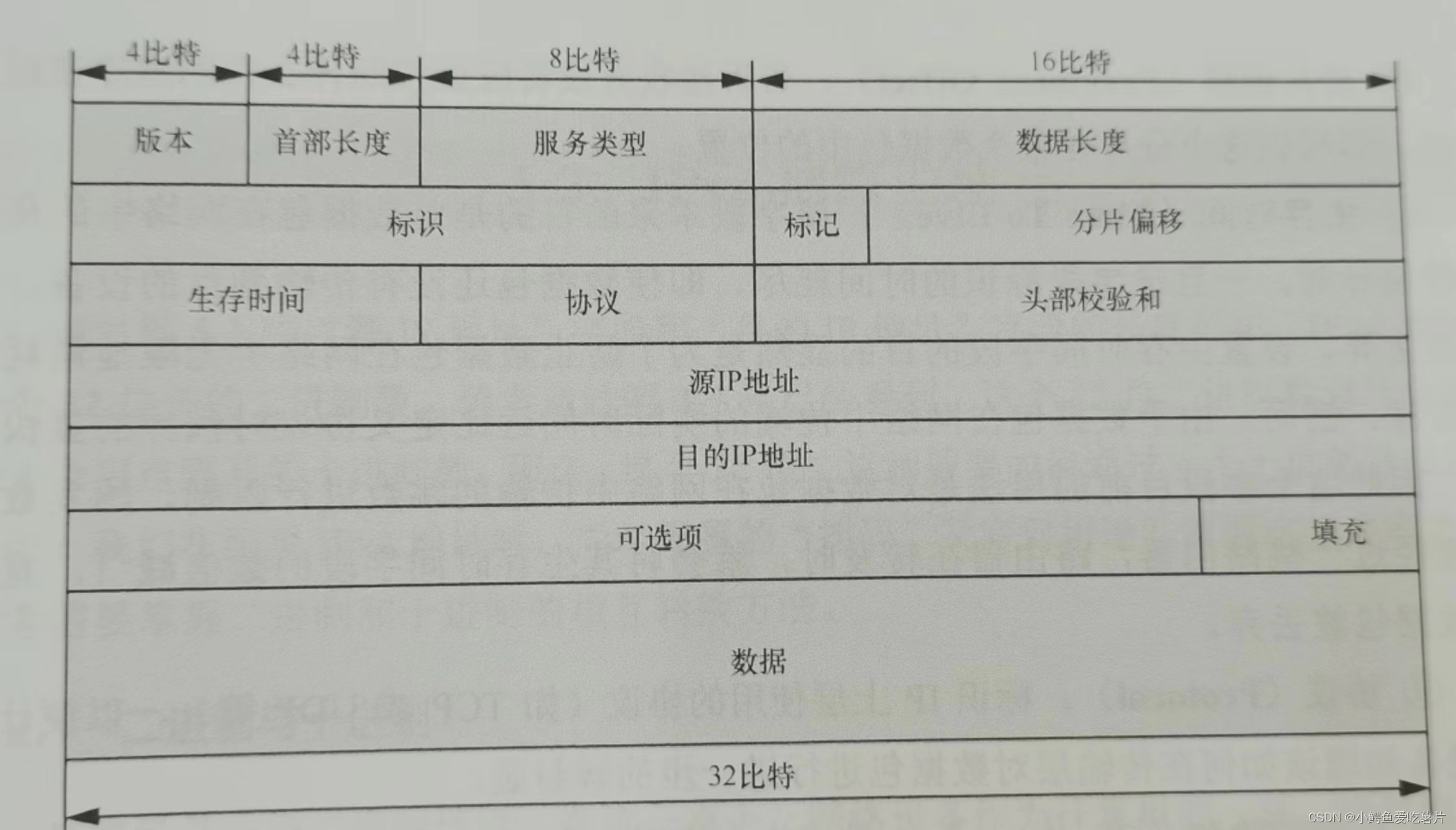
【网络协议】IP
当连接多个异构的局域网形成强烈需求时,用户不满足于仅在一个局域网内进行通信,他们希望通过更高一层协议最终实现异构网络之间的连接。既然需要通过更高一层的协议将多个局域网进行互联,那么这个协议就必须为不同的局域网环境定义统一的寻址…...

Python 布尔类型
布尔值表示两个值之一:True(真)或False(假)。 布尔值 在编程中,您经常需要知道一个表达式是否为True或False。 您可以在Python中评估任何表达式,并获得两个答案之一:True或False。…...

iOS设备管理器iMazing比iTunes好用吗?有哪些优势
虽然 iTunes 是 Apple 官方指定的 iPhone 数据备份和管理工具,但是一直以来 iTunes 卡顿的使用体验和过慢的备份过程为不少人诟病。如果大家也被 iTunes 体验不佳的备份和管理功能所困扰,那么简单易用、功能强大的iMazing 能为你解决这个问题。 iMazing…...

Opengl之深度测试
在坐标系统小节中,我们渲染了一个3D箱子,并且运用了深度缓冲(Depth Buffer)来防止被阻挡的面渲染到其它面的前面。在这一节中,我们将会更加深入地讨论这些储存在深度缓冲(或z缓冲(z-buffer))中的深度值(Depth Value),以及它们是如何确定一个片段是处于其它片段后方的。 …...

利用ICG-NH2/Amine进行DNA标记1686147-55-6星戈瑞
ICG-NH2(吲哚菁绿胺)可以用于DNA标记,这种标记方法通常涉及到DNA上的胺基反应基团和ICG-NH2之间的化学反应。以下是一种常见的方法,用于利用ICG-NH2标记DNA分子: 步骤: 1.准备目标DNA:你需要准…...

Pyecharts数据可视化
Pyecharts数据可视化 1、Pyecharts模块2、柱状图3、折线图4、饼图5、散点图6、图表合并7、词云8、地图 1、Pyecharts模块 ECharts是百度提供的基于JavaScript的开源可视化库,主要用于Web端数据可视化 Echarts是通过JS实现的,Pyecharts则可以使用Python来…...
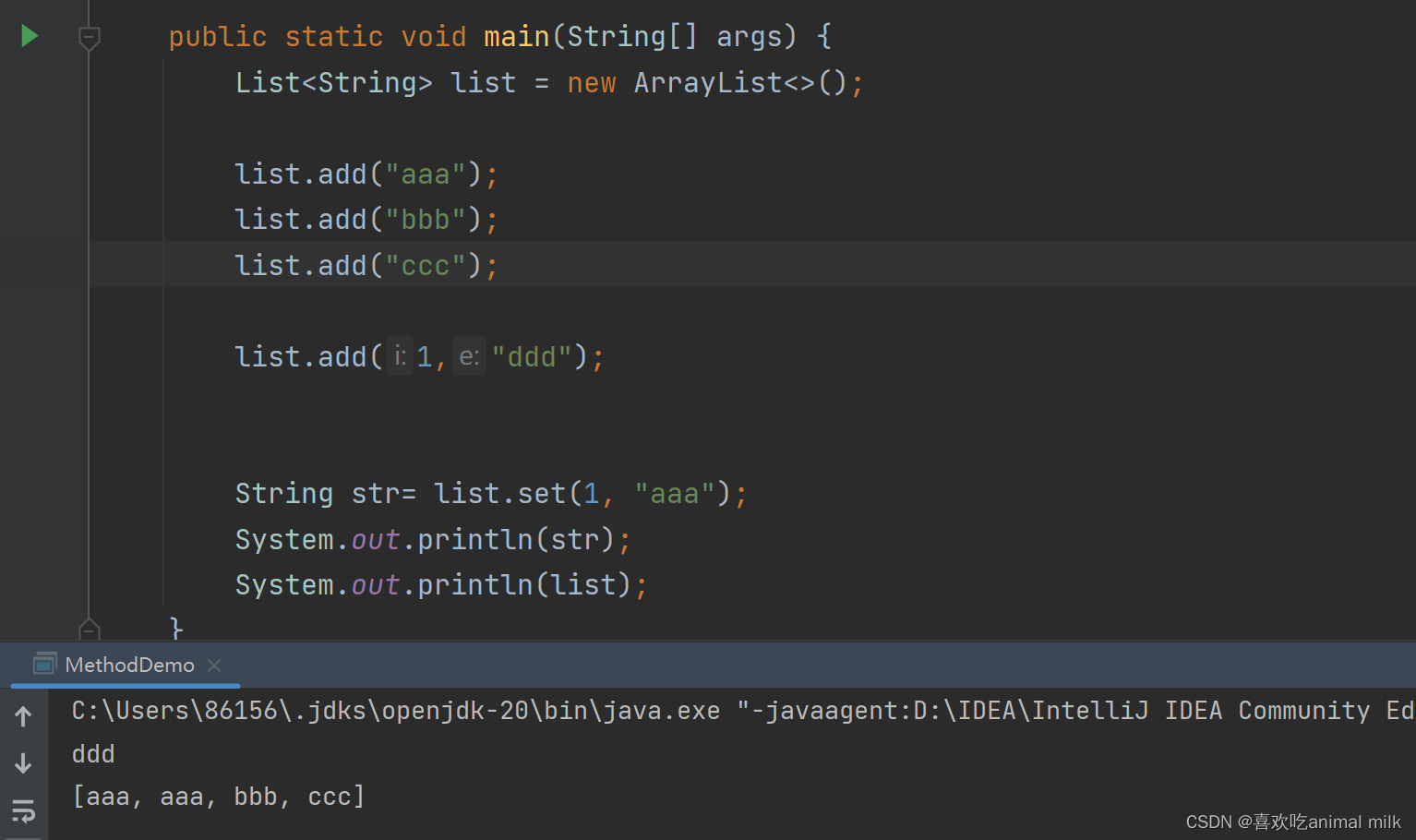
集合-List集合
系列文章目录 1.集合-Collection-CSDN博客 2.集合-List集合-CSDN博客 文章目录 目录 系列文章目录 文章目录 前言 一 . 什么是List? 二 . List集合的特点 三 . 常用方法 1.void add(int index, E element): 将指定的元素插入到列表的指定位置。 2.E remove(int in…...

vuex的使用
1 vuex的使用 1 vuex的使用 store/index.js -在Vue中实现集中式状态(数据)管理的一个Vue插件,对vue应用中多个组件的共享状态进行集中式 的管理(读/写),也是一种组件间通信的方式,且适用于任意…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
