Machine Learning(study notes)
There is no studying without going crazy
Studying alwats drives us crazy
文章目录
- Define
- Machine Learning
- Supervised Learning(监督学习)
- Regression problem
- Classidication
- Unspervised Learning
- Clustering
- Study
- Model representation(模型概述)
- const function
- How to use and t
- solve problem
- gradient descent
Define
Machine Learning
A computer program is said to learn from experience E with respect to some task T and some performance measure P , if its performance on T, as measued
计算机程序从经验E中学习,解决某一任务T进行某一性能度量P,通过P测定在T上的表现因经验E而提高
realy rhyme
Supervised Learning(监督学习)
right answers given
Regression problem
tring to predict continuios valued ouput
需要预测连续的数值输出
in that problem , you should give its some right valued with different classic and machine learning will learn to predict it

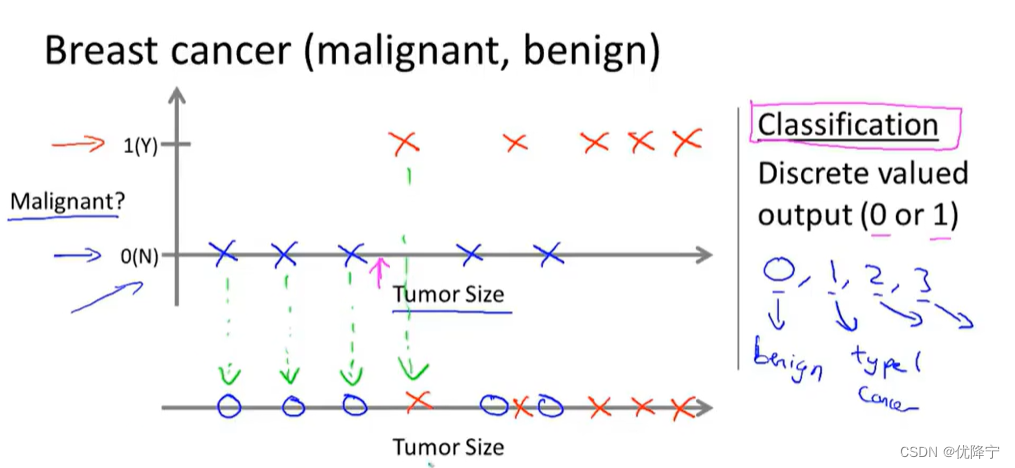
Classidication
discrete valued output (zero or one)
离散取值输出
in that problem, you should give some valued . Different with regression , maybe the type of data
Unspervised Learning
Clustering
maybe using clustring algorithm to break that data into two separate clusters
使用聚类算法将数据分为两簇
do not know what data mean and data features and so on(just about data information),and you know ,machine learning should classification those data into different clusters
the classic problem of that maybe Cocktail party problem algorithm
经典问题就是鸡尾酒派对算法,就是有背景音乐以及人声,能分理分离出两者的声音
Study
Model representation(模型概述)
using this example
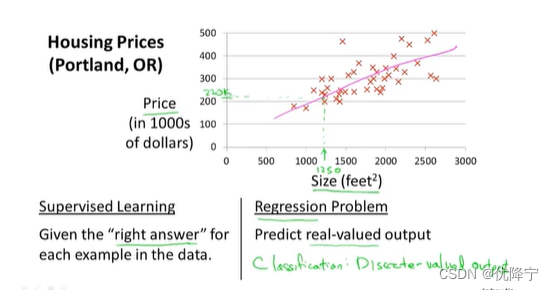
And we will give some training set
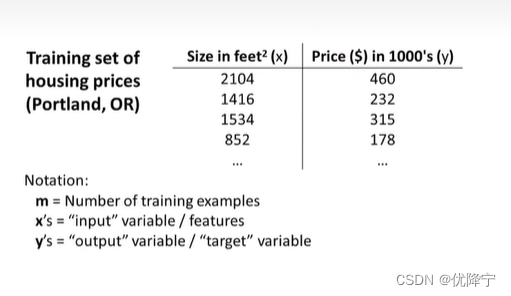
As you can see , we put
m as number of training examples,
x’s as “input” variable / features ,
y’s as “output” variable / “target” variable ,
(x,y) as one training example ,
(x(i),y(i)) refer to the ith training example.(this superscript i over here , this is not exponentiation.The superscript i in parenthess that’s just an index into my training set)
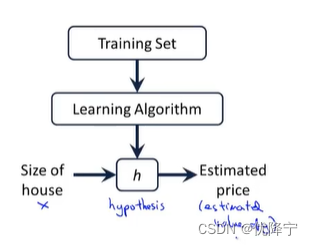
We saw that with the training set like our training set of housing prices and we feed that to our learning algorithm.Is the job of a learning algorithm to then output a function which by convention is usually denoted lowercase h
const function
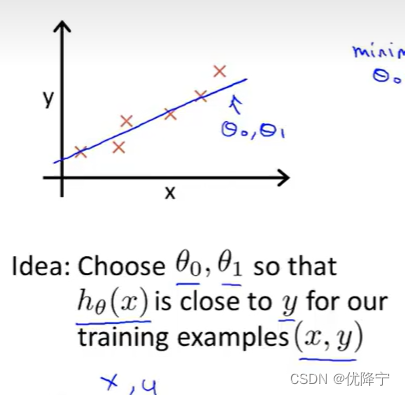
In this chart , we want the difference between h(x) and y to be small .And one thing I’m gonna do is try to minimize the square difference between the output of the hypothesis and the actual price of the house.

What we want to do is minimize over theta zero and theta one my function J of theta zero comma theta one
error cost function is probably the most commonly used one for regeression problem
How to use and t
solve problem
gradient descent
It turns out gradient descent is a more general algorithm, and is used not only in linear regression. It’s actually used all over the place in machine learning.

Here is the problem setup.
We are going to see that we have some function J of (θ0,θ1). Maybe it is a cost function from linear regression.And we want to come up with an algorithm for minimizing that as a function of J of (θ0,θ1).
For the sake of brevity , for the sake of your succinctness of notation , so we just goingn to pretend that have only two parameters through the rest of this video.
The idea for gradient descent :
What we’re going to do is we are going to strat off with some initial guesses for θ0 and θ1.
What we are going to do in gradient descent is we’ll keep changing θ0 and θ1 a little bit to try to reduce J of (θ0,θ1)
相关文章:

Machine Learning(study notes)
There is no studying without going crazy Studying alwats drives us crazy 文章目录 DefineMachine LearningSupervised Learning(监督学习)Regression problemClassidication Unspervised LearningClustering StudyModel representation(…...

centos7通过docker搭建nginx+php环境
以下环境都是基于centos7.9完成。 1.安装docker yum install docker-ce 说明:这一步,由于centos软件仓库没有收纳docker,需要自己去官网爬文档安装。 安装完成之后,就是启动docker服务以及添加到开机启动。 systemctl enable do…...

Node.js 学习笔记
小插件Template String Converter 当输入${}时,自动为其加上 反引号 一、node入门 node.js是什么 node的作用 开发服务器应用 开发工具类应用 开发桌面端应用 1.命令行工具 命令的结构 常用命令 切换到D盘——D: 查看D盘目录——dir 切换工作目录——c…...

RabbitMQ之发布确认高级
RabbitMQ之发布确认高级 一、发布确认 SpringBoot 版本1.1 确认机制方案1.2 代码架构图1.3 配置文件1.4 添加配置类1.5 消息生产者1.6 回调接口1.7 消息消费者1.8 结果分析 二、回退消息2.1 Mandatory 参数2.2 消息生产者代码2.3 回调接口2.4 结果分析 三、备份交换机3.1 代码架…...
lv5 嵌入式开发-10 信号机制(下)
目录 1 信号集、信号的阻塞 2 信号集操作函数 2.1 自定义信号集 2.2 清空信号集 2.3 全部置1 2.4 将一个信号添加到集合中 2.5 将一个信号从集合中移除 2.6 判断一个信号是否在集合中 2.7 设定对信号集内的信号的处理方式(阻塞或不阻塞) 2.8 使进程挂起(…...

【postgresql】 ERROR: multiple assignments to same column “XXX“
Cause: org.postgresql.util.PSQLException: ERROR: multiple assignments to same column "XXX"; bad SQL grammar []; nested exception is org.postgresql.util.PSQLException: ERROR: multiple assignments to same column "XXX"; 原因:or…...
一文读懂Llama 2(从原理到实战)
简介 Llama 2,是Meta AI正式发布的最新一代开源大模型。 Llama 2训练所用的token翻了一倍至2万亿,同时对于使用大模型最重要的上下文长度限制,Llama 2也翻了一倍。Llama 2包含了70亿、130亿和700亿参数的模型。Meta宣布将与微软Azure进行合…...
完整指南:如何使用 Node.js 复制文件
文件拷贝指的是将一个文件的数据复制到另一个文件中,使目标文件与源文件内容一致。Node.js 提供了文件系统模块 fs,通过该模块可以访问文件系统,实现文件操作,包括拷贝文件。 Node.js 中文件拷贝方法 在 Node.js 中,有…...

ElementUI - 主页面--动态树右侧内容管理
一.左侧动态树 1.定义组件 ①样式&数据处理 <template><el-menu class"el-menu-vertical-demo" background-color"#334157"text-color"#fff" active-text-color"#ffd04b" :collapse"collapsed" router :def…...

全国排名前三的直播公司无锋科技入驻天府蜂巢成都直播产业基地
最近,全国排名前三的直播公司——无锋科技,正式宣布入驻位于成都的天府蜂巢直播产业基地,这一消息引起了业内人士的高度关注。成都直播产业基地一直是中国直播产业的重要地标之一,其强大的技术和资源优势为众多直播公司提供了广阔…...

机器人中的数值优化|【五】BFGS算法非凸/非光滑处理
机器人中的数值优化|【五】BFGS算法的非凸/非光滑处理 往期内容回顾 机器人中的数值优化|【一】数值优化基础 机器人中的数值优化|【二】最速下降法,可行牛顿法的python实现,以Rosenbrock function为例 机器人中的数值优化|【三】无约束优化࿰…...
ESP32S3的MPU-6050组件移植教程
前言 (1)实习公司要搞ESP32BOX的驱动移植,所有资料自己找还是比较折磨人的现在我分享几个官方的组件移植资料: <1>Find the most exciting ESP-IDF components(ESP32的官方组件都可以在里面查,按照他…...
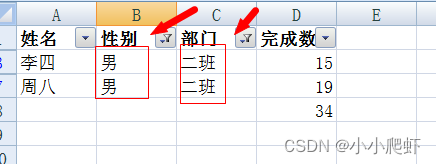
excel筛选后求和
需要对excel先筛选,后对“完成数量”进行求和。初始表格如下: 一、选中表内任意单元格,按ctrlshiftL,开启筛选 二、根据“部门”筛选,比如选择“一班” 筛选完毕后,选中上图单元格,然后按alt后&…...

pyspark 检测任务输出目录是否空,避免读取报错
前言 在跑调度任务时候,有时候子任务需要依赖前置任务的输出,但类似读取 Parquet 或者 Orc 文件时,如果不判断目录是否为空,在输出为空时会报错,所以需要 check 一下,此外Hadoop通常在写入数据时会在目录中…...

「网页开发|前端开发|Vue」10 vuex模块化:将数据划分成不同modules分别管理
本文主要介绍如何使用vuex的modules将状态数据根据不同模块进行划分并分别管理以及如何使用mapGetters快速将状态管理中的数据导入成local变量。 文章目录 本系列前文传送门一、场景说明二、使用modules划分不同模块三、使用Getters获取状态管理数据Getter传参mapGetters 辅助…...

苹果CMS插件-苹果CMS全套插件免费
网站内容的生成和管理对于网站所有者和内容创作者来说是一个挑战。有一些强大的工具可以帮助您轻松地解决这些问题。苹果CMS插件自动采集插件、采集发布插件以及采集伪原创发布插件,是这些工具之一。它们不仅可以极大地节省您的时间和精力,还可以提高您网…...

域环境介绍
一、概述 内网也指局域网,指的是某个区域由多台计算机互连而成的计算机组,范围通常在数千米以内,在局域网中,可以实现文件管理,应用软件共享,打印机共享、工作组内的日程安排、电子邮件和传真通信服务等&a…...

地球同步静止轨道上的中国卫星
3万6千公里地球同步静止轨道上的中国控制的卫星(包括香港属非国产平台卫星、外国属中国平台卫星),共80颗;截止到2023年8月3日,共有563颗在轨卫星。 号定位名称发射时间用途重量1141.1W中星1C(FH2C)2015.12.10DFH4平台…...
)
HAProxy代理TCP(使用HAProxy 为TiDB-Server 做负载均衡)
目录 一、使用HAProxy 为TiDB-Server 做负载均衡环境1、创建文件夹2、配置haproxy.cfg3、创建 docker-compose.yaml 文件haproxy.cfg 配置说明[参照官方文档](https://pingcap.com/docs-cn/v3.0/reference/best-practices/haproxy/ "参照官方文档") 一、使用HAProxy …...

全新自适应导航网模板 导航网系统源码 网址导航系统源码 网址目录网系统源码
高价值目录网导航网整站源码 | 2999元价值,最新版本源码下载推荐 1、导航网一键获取目标站SEO信息,7.5版本增加会员中心一键获取网站信息网站权重,增加小程序提交发布,全新自适应模板; 2、可设置游客提交、游客提交人工审核,会员免审提交,会员提交人工审核,VIP会员免…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
