【C++哈希应用】位图、布隆过滤器
【C++哈希应用】位图、布隆过滤器
目录
- 【C++哈希应用】位图、布隆过滤器
- 位图概念
- 位图的实现
- 位图改造
- 位图应用总结
- 布隆过滤器
- 布隆过滤器的提出
- 布隆过滤器的概念
- 布隆过滤器的查找
- 布隆过滤器删除
- 布隆过滤器优点
- 布隆过滤器缺陷
作者:爱写代码的刚子
时间:2023.9.30
前言:本篇博客介绍hash应用部分——位图和布隆过滤器,利用位图和布隆过滤器解决一些特定场景的问题。
位图概念
所谓位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的。
数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,那么可以使用一个二进制比 特位来代表数据是否存在的信息,如果二进制比特位为1,代表存在,为0代表不存在。比如:
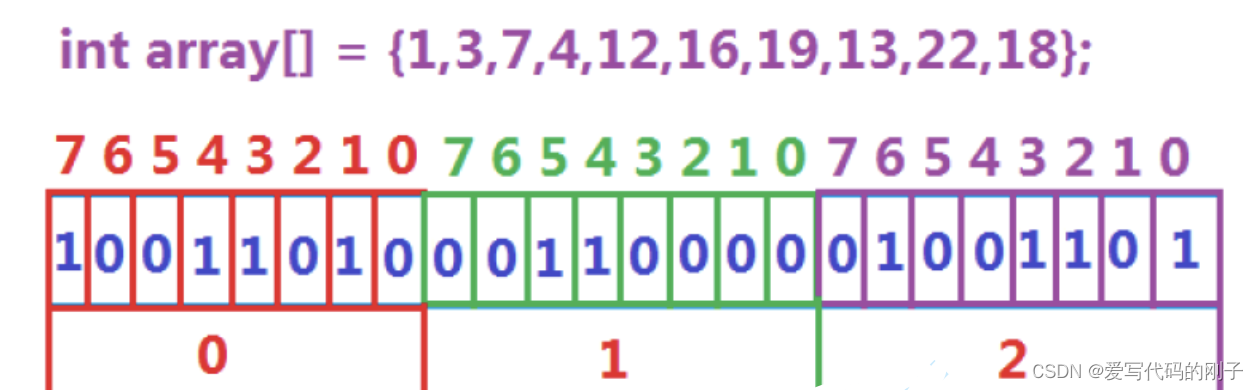
位图的实现
template<size_t N>class bitset{public:bitset(){_a.resize(N/32+1);//不要忘了+1,默认初始化成0}void set( size_t x){int i=x/32;int j=x%32;_a[i] |=(1<<j);}void reset(size_t x){int i=x/32;int j=x%32;_a[i] &= (~(1<<j));}bool test(size_t x){int i=x/32;int j=x%32;return _a[i] &(1<<j);}private:vector<int> _a; };
位图改造
用两个位图来测试数据个数
template<size_t N>class twobitset{public:void set(size_t x){//00->01if(!_b1.test(x)&&!_b2.test(x)){_b2.set(x);}//01->10else if(!_b1.test(x)&&_b2.test(x)){_b1.set(x);_b2.reset(x);}}bool is_once(size_t x){return !_b1.test(x)&&_b2.test(x);}bool is_or_above_twice(size_t x){return _b1.test(x)&&!_b2.test(x);}private:bitset<N> _b1;bitset<N> _b2;};
位图应用总结
- 快速查找某个数据是否在一个集合中
- 排序
- 求两个集合的交集、并集等
- 操作系统中磁盘块标记
布隆过滤器
布隆过滤器的提出
我们在使用新闻客户端看新闻时,它会给我们不停地推荐新的内容,它每次推荐时要去重,去掉那些已经看过的内容。问题来了,新闻客户端推荐系统如何实现推送去重的? 用服务器记录了用户看过的所有历史记 录,当推荐系统推荐新闻时会从每个用户的历史记录里进行筛选,过滤掉那些已经存在的记录。 如何快速查找呢?
- 用哈希表存储用户记录,缺点:浪费空间
- 用位图存储用户记录,缺点:不能处理哈希冲突 3. 将哈希与位图结合,即布隆过滤器
布隆过滤器的概念
布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结 构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用多个哈希函 数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间
// 假设布隆过滤器中元素类型为K,每个元素对应5个哈希函数
template<class K, class KToInt1 = KeyToInt1, class KToInt2 = KeyToInt2,class KToInt3 = KeyToInt3, class KToInt4 = KeyToInt4,class KToInt5 = KeyToInt5>
class BloomFilter
{
public:BloomFilter(size_t size) // 布隆过滤器中元素个数 : _bmp(5*size), _size(0){}bool Insert(const K& key){size_t bitCount = _bmp.Size();size_t index1 = KToInt1()(key)%bitCount;size_t index2 = KToInt2()(key)%bitCount;size_t index3 = KToInt3()(key)%bitCount;size_t index4 = KToInt4()(key)%bitCount;size_t index5 = KToInt5()(key)%bitCount;_bmp.Set(index1); _bmp.Set(index2);_bmp.Set(index3);_bmp.Set(index4);_bmp.Set(index5);_size++;}
private:bitset _bmp;size_t _size;// 实际元素的个数
}
布隆过滤器的查找
布隆过滤器的思想是将一个元素用多个哈希函数映射到一个位图中,因此被映射到的位置的比特位一定为1。 所以可以按照以下方式进行查找:分别计算每个哈希值对应的比特位置存储的是否为零,只要有一个为零, 代表该元素一定不在哈希表中,否则可能在哈希表中。
bool IsInBloomFilter(const K& key)
{size_t bitCount = _bmp.Size();size_t index1 = KToInt1()(key)%bitCount;if(!_bmp.Test(index1))return false;size_t index2 = KToInt2()(key)%bitCount;if(!_bmp.Test(index2))return false;size_t index3 = KToInt3()(key)%bitCount;if(!_bmp.Test(index3))return false;size_t index4 = KToInt4()(key)%bitCount;if(!_bmp.Test(index4))return false;size_t index5 = KToInt5()(key)%bitCount;if(!_bmp.Test(index5))
return false; return true; // 有可能在
}
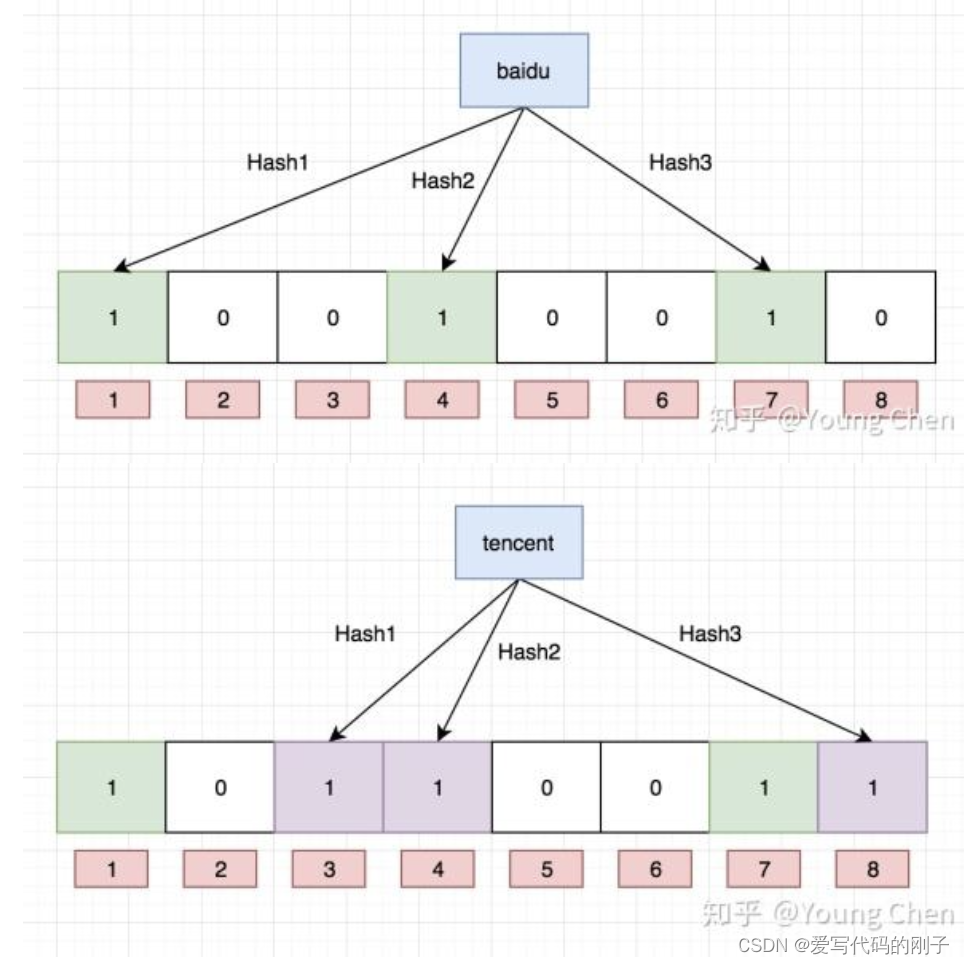
注意:布隆过滤器如果说某个元素不存在时,该元素一定不存在,如果该元素存在时,该元素可能存在,因为有些哈希函数存在一定的误判。比如:在布隆过滤器中查找"alibaba"时,假设3个哈希函数计算的哈希值为:1、3、7,刚好和其他元素的比特位重叠,此时布隆过滤器告诉该元素存在,但实该元素是不存在的。
布隆过滤器删除
布隆过滤器不能直接支持删除工作,因为在删除一个元素时,可能会影响其他元素。
比如:删除上图中"tencent"元素,如果直接将该元素所对应的二进制比特位置0,“baidu”元素也被删除了, 因为这两个元素在多个哈希函数计算出的比特位上刚好有重叠。
一种支持删除的方法:将布隆过滤器中的每个比特位扩展成一个小的计数器,插入元素时给k个计数器(k个哈希函数计算出的哈希地址)加一,删除元素时,给k个计数器减一,通过多占用几倍存储空间的代价来增加删除操作。
缺陷:
- 无法确认元素是否真正在布隆过滤器中
- 存在计数回绕
布隆过滤器优点
-
增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无关
-
哈希函数相互之间没有关系,方便硬件并行运算
-
布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势
-
在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势
-
数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
-
使用同一组散列函数的布隆过滤器可以进行交、并、差运算
布隆过滤器缺陷
- 有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再建立一个白 名单,存储可能会误判的数据)
- 不能获取元素本身
- 一般情况下不能从布隆过滤器中删除元素
- 如果采用计数方式删除,可能会存在计数回绕问题
附:
一致性哈希
哈希与加密
相关文章:

【C++哈希应用】位图、布隆过滤器
【C哈希应用】位图、布隆过滤器 目录 【C哈希应用】位图、布隆过滤器位图概念位图的实现位图改造位图应用总结布隆过滤器布隆过滤器的提出布隆过滤器的概念布隆过滤器的查找布隆过滤器删除布隆过滤器优点布隆过滤器缺陷 作者:爱写代码的刚子 时间:2023.9…...
‘)
Qt 编译纯c的C99的项目, error: undefined reference to `f()‘
把Cpp的后缀该为C是什么样的 尝试引用一个奇门排盘的c程序,在git上找到的叫cqm, 然后总是报错 error: undefined reference to f() 很是郁闷 于是新建了个项目试验一下,终于摸清了需要命名空间。 后来这么写就可以了 a.h namespace XX …...
TensorFlow入门(五、指定GPU运算)
一般情况下,下载的TensorFlow版本如果是GPU版本,在运行过程中TensorFlow能自动检测。如果检测到GPU,TensorFlow会默认利用找到的第一个GPU来执行操作。如果机器上有超过一个可用的GPU,除第一个之外的其他GPU默认是不参与计算的。如果想让TensorFlow使用这些GPU执行操作,需要将运…...
Unity - 实践: Metallic流程贴图 转 Specular流程贴图
文章目录 目的Metallic Flow - SP - 输出输出的 MRA (MGA) 贴图 Metallic->Specular (根据教程一步一步实践)1. Base color Metallic -> Diffuse2. Base color Metallic -> Specular3. Roughness -> Glossiness输出贴图,在 unity 中展示:M…...
)
第三章:最新版零基础学习 PYTHON 教程(第四节 - Python 运算符—Python 逻辑运算符及示例)
运算符用于对值和变量执行操作。这些是执行算术和逻辑计算的特殊符号。运算符运算的值称为操作数。 表中的内容逻辑运算符 逻辑与运算符 逻辑或运算符 逻辑非运算符 逻辑运算符的求值顺序 逻辑运算符 在 Python 中,逻辑运算符用于条件语句(True 或 False)。它们执行逻辑 AN…...
功能测试 (Functional Testing, FT))
如何做好测试?(三)功能测试 (Functional Testing, FT)
1. 功能测试的详细介绍: 功能测试 (Functional Testing, FT),是一种软件测试方法,旨在验证系统的功能是否按照需求规格说明书或用户期望的方式正常工作。它关注系统的整体行为,以确保各个功能模块和组件之间的交互和集成正确。 …...

Ubuntu-Server-22.04安装桌面+VNC
前提:Ubuntu Server安装好后,ubantu其他版本是否适用这里未知,欢迎大佬们前来评论 一、默认没有图形界面,有时觉得用图形界面操作更简单直接,于是用如下命令安装: 1.更新本地环境 sudo apt-get update s…...
职业规划,什么是职业兴趣 - 我喜欢做什么?
能够在工作岗位上面做出成绩的人,都是结合自身兴趣,对职业进行合理规划的那一类。尤其是步入中年以后,能够创造出巨大价值的人,无一例外都是喜欢自己职业的人。没有将兴趣融入工作的人,只能够忍受默默无闻地活着&#…...

基于Java的高校学生党员发展流程管理系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...

【NLP的python库(03/4) 】: 全面概述
一、说明 Python 对自然语言处理库有丰富的支持。从文本处理、标记化文本并确定其引理开始,到句法分析、解析文本并分配句法角色,再到语义处理,例如识别命名实体、情感分析和文档分类,一切都由至少一个库提供。那么,你…...

面试理论篇三
关于异常机制篇 异常描述 目录 关于异常机制篇异常描述 注:自用 1,Java中的异常分为哪几类?各自的特点是什么? Java中的异常 可以分为 可查异常(Checked Exception)、运行时异常(Runtime Exception) 和 错误(Error)三类。可查异…...

ShardingSphere|shardingJDBC - 在使用数据分片功能情况下无法配置读写分离
问题场景: 最近在学习ShardingSphere,跟着教程一步步做shardingJDBC,但是想在开启数据分片的时候还能使用读写分离,一直失败,开始是一直能读写分离,但是分偏见规则感觉不生效,一直好像是走不进去…...

char s1[len + 1]; 报错说需要常量?
在C中,字符数组的大小必须是常量表达式,不能使用变量 len 作为数组大小。为了解决这个问题,你可以使用 new 运算符动态分配字符数组的内存,但在使用完后需要手动释放。 还有啥是只能这样的,还是说所有的动态都需要new&…...

【Linux】CentOS-6.8超详细安装教程
文章目录 1.CentOS介绍:2.必要准备:3.创建虚拟机:4 .安装系统 1.CentOS介绍: CentOS是一种基于开放源代码的Linux操作系统,它以其稳定性、安全性和可靠性而闻名,它有以下特点: 开源性࿱…...

【Java 进阶篇】MySQL启动与关闭、目录结构以及 SQL 相关概念
MySQL 服务启动与关闭 MySQL是一个常用的关系型数据库管理系统,通过启动和关闭MySQL服务,可以控制数据库的运行状态。本节将介绍如何在Windows和Linux系统上启动和关闭MySQL服务。 在Windows上启动和关闭MySQL服务 启动MySQL服务 在Windows上&#x…...

Android 11.0 mt6771新增分区功能实现一
1.前言 在11.0的系统开发中,在对某些特殊模块中关于数据的存储方面等需要新增分区来保存, 所以就需要在系统分区新增分区,接下来就来实现这个功能 2.mt6771新增分区功能实现一的核心类 build/make/core/Makefile build/make/core/board_config.mk build/make/core/config…...

LiveData简单使用
1.LiveData是基于观察者模式,可以用于处理消息的订阅分发的组件。 LiveData组件有以下特性: 1) 可以感知Activity、Fragment生命周期变化,因为他把自己注册成LifecycleObserver。 2) LiveData可以注册多个观察者,只有数据…...
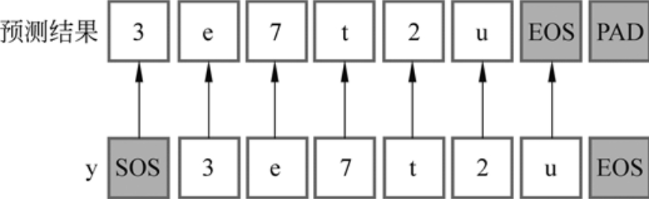
手动实现Transformer
Transformer和BERT可谓是LLM的基础模型,彻底搞懂极其必要。Transformer最初设想是作为文本翻译模型使用的,而BERT模型构建使用了Transformer的部分组件,如果理解了Transformer,则能很轻松地理解BERT。 一.Transformer模型架构 1…...

leetcode456 132 Pattern
给定数组,找到 i < j < k i < j < k i<j<k,使得 n u m s [ i ] < n u m s [ k ] < n u m s [ j ] nums[i] < nums[k] < nums[j] nums[i]<nums[k]<nums[j] 最开始肯定想着三重循环,时间复杂度 O ( n 3 )…...

WordPress外贸建站Astra免费版教程指南(2023)
在WordPress的外贸建站主题中,有许多备受欢迎的主题,如AAvada、Astra、Hello、Kadence等最佳WordPress外贸主题,它们都能满足建站需求并在市场上广受认可。然而,今天我要介绍的是一个不断颠覆建站人员思维的黑马——Astra主题。 …...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...
