【索引】常见的索引、B+树结构、什么时候需要使用索引、优化索引方法、索引主要的数据结构、聚簇索引、二级索引、创建合适的索引等重点知识汇总
目录
索引的分类
什么时候需要 / 不需要创建索引?
有什么优化索引的方法
MySQL索引主要使用的两种数据结构是什么
为什么 MySQL 采用 B+ 树作为索引
聚簇索引和二级索引
根据给定的表,如何创建索引比较好
索引的分类
- 普通索引:最基本的索引,没有任何限制
- 唯⼀索引:与普通索引类似,但索引列的值必须是唯⼀的,允许空值
- 主键索引:⼀种特殊的唯⼀索引,⼀个表只能有⼀个主键,不允许有空值
- 组合索引:在多个字段上创建的索引,只有在查询条件中使⽤了创建索引的第⼀个字段,索引才会被使⽤
- 全⽂索引:主要⽤来查找⽂本中的关键字,类似于搜索引擎
- 普通索引:仅加速查询
- 唯一索引:加速查询 + 列值唯一(可以有null)
- 主键索引:加速查询 + 列值唯一(不可以有null)+ 表中只有一个
- 组合索引:多列值组成一个索引,专门用于组合搜索,其效率大于索引合并
- 全文索引:对文本的内容进行分词,进行搜索
- 索引合并:使用多个单列索引组合搜索
- 覆盖索引:select的数据列只用从索引中就能够取得,不必读取数据行,换句话说查询列要被所建的索引覆盖
- 聚簇索引:表数据是和主键一起存储的,主键索引的叶结点存储行数据(包含了主键值),二级索引的叶结点存储行的主键值。使用的是B+树作为索引的存储结构,非叶子节点都是索引关键字,但非叶子节点中的关键字中不存储对应记录的具体内容或内容地址。叶子节点上的数据是主键与具体记录(数据内容)
什么时候需要 / 不需要创建索引?
索引最大的好处是提高查询速度,但是索引也是有缺点的,比如:
- 需要占用物理空间,数量越大,占用空间越大;
- 创建索引和维护索引要耗费时间,这种时间随着数据量的增加而增大;
- 会降低表的增删改的效率,因为每次增删改索引,B+ 树为了维护索引有序性,都需要进行动态维护。
什么时候适用索引?
- 字段有唯一性限制的,比如商品编码;
- 经常用于 WHERE 查询条件的字段,这样能够提高整个表的查询速度,如果查询条件不是一个字段,可以建立联合索引。
- 经常用于 GROUP BY 和 ORDER BY 的字段,这样在查询的时候就不需要再去做一次排序了,因为我们都已经知道了建立索引之后在 B+Tree 中的记录都是排序好的。
什么时候不需要创建索引?
- WHERE 条件,GROUP BY,ORDER BY 里用不到的字段,索引的价值是快速定位,如果起不到定位的字段通常是不需要创建索引的,因为索引是会占用物理空间的。
- 字段中存在大量重复数据,不需要创建索引,比如性别字段,只有男女,如果数据库表中,男女的记录分布均匀,那么无论搜索哪个值都可能得到一半的数据。在这些情况下,还不如不要索引,因为 MySQL 还有一个查询优化器,查询优化器发现某个值出现在表的数据行中的百分比很高的时候,它一般会忽略索引,进行全表扫描。
- 表数据太少的时候,不需要创建索引;
- 经常更新的字段不用创建索引,比如不要对电商项目的用户余额建立索引,因为索引字段频繁修改,由于要维护 B+Tree的有序性,那么就需要频繁的重建索引,这个过程是会影响数据库性能的。
有什么优化索引的方法
这里说一下几种常见优化索引的方法:
- 前缀索引进行优化;
- 覆盖索引进行优化;
- 主键索引最好是自增的;
- 防止索引失效;
前缀索引进行优化
前缀索引顾名思义就是使用某个字段中字符串的前几个字符建立索引,那我们为什么需要使用前缀来建立索引呢?
使用前缀索引是为了减小索引字段大小,可以增加一个索引页中存储的索引值,有效提高索引的查询速度。在一些大字符串的字段作为索引时,使用前缀索引可以帮助我们减小索引项的大小。
不过,前缀索引有一定的局限性,例如:
- order by 就无法使用前缀索引;
- 无法把前缀索引用作覆盖索引;
覆盖索引进行优化
覆盖索引是指 SQL 中 query 的所有字段,在索引 B+Tree 的叶子节点上都能找得到的那些索引,从二级索引中查询得到记录,而不需要通过聚簇索引查询获得,可以避免回表的操作。这种索引设计能够显著提高查询性能,因为它减少了磁盘I/O操作和数据的传输。
假设我们只需要查询商品的名称、价格,有什么方式可以避免回表呢?
我们可以建立一个联合索引,即「商品ID、名称、价格」作为一个联合索引。如果索引中存在这些数据,查询将不会再次检索主键索引,从而避免回表。
所以,使用覆盖索引的好处就是,不需要查询出包含整行记录的所有信息,也就减少了大量的 I/O 操作。
主键索引最好是自增的
我们在建表的时候,都会默认将主键索引设置为自增的,具体为什么要这样做呢?又什么好处?
InnoDB 创建主键索引默认为聚簇索引,数据被存放在了 B+Tree 的叶子节点上。也就是说,同一个叶子节点内的各个数据是按主键顺序存放的,因此,每当有一条新的数据插入时,数据库会根据主键将其插入到对应的叶子节点中。
如果我们使用自增主键,那么每次插入的新数据就会按顺序添加到当前索引节点的位置,不需要移动已有的数据,当页面写满,就会自动开辟一个新页面。因为每次插入一条新记录,都是追加操作,不需要重新移动数据,因此这种插入数据的方法效率非常高。
如果我们使用非自增主键,由于每次插入主键的索引值都是随机的,因此每次插入新的数据时,就可能会插入到现有数据页中间的某个位置,这将不得不移动其它数据来满足新数据的插入,甚至需要从一个页面复制数据到另外一个页面,我们通常将这种情况称为页分裂。页分裂还有可能会造成大量的内存碎片,导致索引结构不紧凑,从而影响查询效率。
另外,主键字段的长度不要太大,因为主键字段长度越小,意味着二级索引的叶子节点越小(二级索引的叶子节点存放的数据是主键值),这样二级索引占用的空间也就越小。
索引最好设置为 NOT NULL
为了更好的利用索引,索引列要设置为 NOT NULL 约束。有两个原因:
- 第一原因:索引列存在 NULL 就会导致优化器在做索引选择的时候更加复杂,更加难以优化,因为可为 NULL 的列会使索引、索引统计和值比较都更复杂,比如进行索引统计时,count 会省略值为NULL 的行。
- 第二个原因:NULL 值是一个没意义的值,但是它会占用物理空间,所以会带来的存储空间的问题,因为 InnoDB 存储记录的时候,如果表中存在允许为 NULL 的字段,那么行格式(opens new window)中至少会用 1 字节空间存储 NULL 值列表。
防止索引失效
用上了索引并不意味着查询的时候会使用到索引,所以我们心里要清楚有哪些情况会导致索引失效,从而避免写出索引失效的查询语句,否则这样的查询效率是很低的。
这里简单说一下,发生索引失效的情况:
- 当我们使用左或者左右模糊匹配的时候,也就是 like %xx 或者 like %xx%这两种方式都会造成索引失效;
- 当我们在查询条件中对索引列做了计算、函数、类型转换操作,这些情况下都会造成索引失效;
- 联合索引要能正确使用需要遵循最左匹配原则,也就是按照最左优先的方式进行索引的匹配,否则就会导致索引失效。
- 在 WHERE 子句中,如果在 OR 前的条件列是索引列,而在 OR 后的条件列不是索引列,那么索引会失效。
我上面说的是常见的索引失效场景,实际过程中,可能会出现其他的索引失效场景,这时我们就需要查看执行计划👇,通过执行计划显示的数据判断查询语句是否使用了索引。
执行计划的主要目的是帮助数据库管理员和开发人员理解数据库系统是如何执行查询的,以便优化查询性能。通过分析执行计划,可以识别潜在的性能问题、查询瓶颈和索引失效等。
在MySQL命令行或查询编辑器中,输入要分析的SQL查询,并在查询之前添加EXPLAIN关键字。例如:
EXPLAIN SELECT * FROM your_table WHERE some_column = 'some_value';
对于执行计划,参数有:
- possible_keys 字段表示可能用到的索引;
- key 字段表示实际用的索引,如果这一项为 NULL,说明没有使用索引;
- key_len 表示索引的长度;
- rows 表示扫描的数据行数。
- type 表示数据扫描类型,我们需要重点看这个。
type 字段就是描述了找到所需数据时使用的扫描方式是什么,常见扫描类型的执行效率从低到高的顺序为:
- All(全表扫描);
- index(全索引扫描);
- range(索引范围扫描);
- ref(非唯一索引扫描);
- eq_ref(唯一索引扫描);
- const(结果只有一条的主键或唯一索引扫描)。
在这些情况里,all 是最坏的情况,因为采用了全表扫描的方式。index 和 all 差不多,只不过 index 对索引表进行全扫描,这样做的好处是不再需要对数据进行排序,但是开销依然很大。所以,要尽量避免全表扫描和全索引扫描。
range 表示采用了索引范围扫描,一般在 where 子句中使用 < 、>、in、between 等关键词,只检索给定范围的行,属于范围查找。从这一级别开始,索引的作用会越来越明显,因此我们需要尽量让 SQL 查询可以使用到 range 这一级别及以上的 type 访问方式。
ref 类型表示采用了非唯一索引,或者是唯一索引的非唯一性前缀,返回数据返回可能是多条。因为虽然使用了索引,但该索引列的值并不唯一,有重复。这样即使使用索引快速查找到了第一条数据,仍然不能停止,要进行目标值附近的小范围扫描。但它的好处是它并不需要扫全表,因为索引是有序的,即便有重复值,也是在一个非常小的范围内扫描。
eq_ref 类型是使用主键或唯一索引时产生的访问方式,通常使用在多表联查中。比如,对两张表进行联查,关联条件是两张表的 user_id 相等,且 user_id 是唯一索引,那么使用 EXPLAIN 进行执行计划查看的时候,type 就会显示 eq_ref。
const 类型表示使用了主键或者唯一索引与常量值进行比较,比如 select name from product where id=1。
需要说明的是 const 类型和 eq_ref 都使用了主键或唯一索引,不过这两个类型有所区别,const 是与常量进行比较,查询效率会更快,而 eq_ref 通常用于多表联查中。
MySQL索引主要使用的两种数据结构是什么
哈希索引
对于哈希索引来说,底层的数据结构肯定是哈希表,因此在绝大多数需求为单条记录查询的时候,可以选择哈希索引,查询性能最快;其余大部分场景,建议选择B+Tree索引
B+Tree索引
B+tree索引就是一种将索引值按一定的算法,存入一个树形的数据结构中(二叉树),每次查询都是从树的入口root开始,依次遍历node,获取leaf。
为什么 MySQL 采用 B+ 树作为索引
要设计一个 MySQL 的索引数据结构,不仅仅考虑数据结构增删改的时间复杂度,更重要的是要考虑磁盘 I/0 的操作次数。因为索引和记录都是存放在硬盘,硬盘是一个非常慢的存储设备,我们在查询数据的时候,最好能在尽可能少的磁盘 I/0 的操作次数内完成。
二叉搜索树虽然是一个天然的二分结构,能很好的利用二分查找快速定位数据,但是它存在一种极端的情况,每当插入的元素都是树内最大的元素,就会导致二分查找树退化成一个链表,此时查询复杂度就会从 O(logn)降低为 O(n)。
为了解决二分查找树退化成链表的问题,就出现了自平衡二叉树,保证了查询操作的时间复杂度就会一直维持在 O(logn) 。但是它本质上还是一个二叉树,每个节点只能有 2 个子节点,随着元素的增多,树的高度会越来越高。
而树的高度决定于磁盘 I/O 操作的次数,因为树是存储在磁盘中的,访问每个节点,都对应一次磁盘 I/O 操作,也就是说树的高度就等于每次查询数据时磁盘 IO 操作的次数,所以树的高度越高,就会影响查询性能。
B 树和 B+ 都是通过多叉树的方式,会将树的高度变矮,所以这两个数据结构非常适合检索存于磁盘中的数据。对于有 N 个叶子节点的 B+Tree,其搜索复杂度为O(logdN),其中 d 表示节点允许的最大子节点个数为 d 个。
但是 MySQL 默认的存储引擎 InnoDB 采用的是 B+ 作为索引的数据结构,原因有:
- B+ 树的非叶子节点不存放实际的记录数据,仅存放索引,因此数据量相同的情况下,相比存储即存索引又存记录的 B 树,B+树的非叶子节点可以存放更多的索引,因此 B+ 树可以比 B 树更「矮胖」,查询底层节点的磁盘 I/O次数会更少。
- B+ 树有大量的冗余节点👇(所有非叶子节点都是冗余索引),这些冗余索引让 B+ 树在插入、删除的效率都更高,比如删除根节点的时候,不会像 B 树那样会发生复杂的树的变化;
为什么冗余节点好!
插入操作:当你在B+树中插入一个新的键值对时,通常只需在叶子节点上进行操作,而不需要修改非叶子节点。这是因为所有的键值对都存储在叶子节点上,非叶子节点只包含索引信息。这减少了插入操作中的数据移动,因此插入操作更高效。
删除操作:当你从B+树中删除一个键值对时,也只需在叶子节点上进行操作。如果删除的键值对位于叶子节点上,那么删除操作非常高效。即使你需要删除的键值对位于中间节点,也不会像B树那样引发复杂的树变化,因为中间节点仍然保留了部分冗余索引。
- B+ 树叶子节点之间用双向链表连接了起来,有利于范围查询,而 B 树做不到,要实现范围查询,因此只能通过树的遍历来完成范围查询,这会涉及多个节点的磁盘 I/O 操作,范围查询效率不如 B+ 树。
B+Tree vs Hash
Hash 在做等值查询的时候效率贼快,搜索复杂度为 O(1)。
但是 Hash 表不适合做范围查询,它更适合做等值的查询,这也是 B+Tree 索引要比 Hash 表索引有着更广泛的适用场景的原因。
聚簇索引和二级索引
索引又可以分成聚簇索引(主键索引)和非聚簇索引(二级索引),它们区别就在于叶子节点存放的是什么数据:
- 聚簇索引的叶子节点存放的是实际数据,所有完整的用户记录都存放在聚簇索引的叶子节点;
- 二级索引的叶子节点存放的是主键值,而不是实际数据。
因为表的数据都是存放在聚簇索引的叶子节点里,所以 InnoDB 存储引擎一定会为表创建一个聚簇索引,且由于数据在物理上只会保存一份,所以聚簇索引只能有一个。
InnoDB 在创建聚簇索引时,会根据不同的场景选择不同的列作为索引:
- 如果有主键,默认会使用主键作为聚簇索引的索引键;
- 如果没有主键,就选择第一个不包含 NULL 值的唯一列作为聚簇索引的索引键;
- 在上面两个都没有的情况下,InnoDB 将自动生成一个隐式自增 id 列作为聚簇索引的索引键;
一张表只能有一个聚簇索引,那为了实现非主键字段的快速搜索👇,就引出了二级索引(非聚簇索引/辅助索引),它也是利用了 B+ 树的数据结构,但是二级索引的叶子节点存放的是主键值,不是实际数据。
我们经常需要根据非主键字段来进行查询。这就引入了二级索引
如果学生表的主键是学号,那么主键索引将基于学号字段创建。如果你希望能够根据学生的姓名来进行快速搜索,你可以创建一个基于姓名字段的二级索引。
这样,二级索引将存储姓名与相应的主键(学号)之间的映射关系,从而允许你通过姓名来快速定位到相应的学生记录,而不必扫描整个表。这是数据库中典型的使用情况,以支持多种查询需求。
因此,如果某个查询语句使用了二级索引,但是查询的数据不是主键值,这时在二级索引找到主键值后,需要去聚簇索引中获得数据行,这个过程就叫作「回表」,也就是说要查两个 B+ 树才能查到数据。
不过,当查询的数据是主键值时,因为只在二级索引就能查询到,不用再去聚簇索引查,这个过程就叫作「索引覆盖」,也就是只需要查一个 B+ 树就能找到数据。
根据给定的表,如何创建索引比较好
- 唯一性:对于唯一性约束的字段,例如身份证号或电子邮件地址,应创建唯一索引,以确保数据的完整性。如果尝试插入重复值,数据库将引发唯一性约束冲突。在MySQL中,可以使用UNIQUE关键字来创建唯一性索引。
- CREATE UNIQUE INDEX idx_email ON users (email);
- 频繁用于搜索和过滤的字段:对于经常在WHERE子句中用于搜索和过滤的字段,例如日期、状态或类别,创建索引可以显著提高查询性能。
- 例如,如果有一个订单表,并且经常按订单日期过滤数据,可以在订单日期列上创建索引。
- 外键字段:对于关联表中的外键字段,最好创建索引。这将加速连接操作和JOIN查询。例如,在订单表中的customer_id字段可以被索引,以便快速检索特定客户的订单。
- 不要过度索引:避免过多的索引,因为每个索引都需要额外的存储空间,而且在写操作时需要维护。过多的索引可能会导致写操作性能下降。只创建那些真正需要的索引。
- 组合索引:对于经常使用多个字段进行查询的情况,考虑创建组合索引。组合索引能够提高查询性能,但要确保字段的顺序与查询中的顺序匹配。例如,如果你经常在last_name和first_name上进行查询,可以创建一个组合索引:(last_name, first_name)。
- 空值处理:对于包含大量空值的字段,不建议创建索引,因为它们的查询效率较低。索引通常用于查找具有值的记录。
- 数据量和性能测试:在创建索引之前,通过性能测试来评估查询性能。可以使用数据库查询分析工具来分析查询执行计划和性能瓶颈。根据测试结果和查询需求,决定创建哪些索引以及如何优化它们。
相关文章:

【索引】常见的索引、B+树结构、什么时候需要使用索引、优化索引方法、索引主要的数据结构、聚簇索引、二级索引、创建合适的索引等重点知识汇总
目录 索引的分类 什么时候需要 / 不需要创建索引? 有什么优化索引的方法 MySQL索引主要使用的两种数据结构是什么 为什么 MySQL 采用 B 树作为索引 聚簇索引和二级索引 根据给定的表,如何创建索引比较好 索引的分类 普通索引:最基本的…...

Egg 封装接口返回信息
中间件封装 代码 const msgArr {"200":成功,"401":token失效 } module.exports (option, app) > {return async function(ctx, next) {try{//成功是返回的信息ctx.emit(code,data,msg)>{console.log(1111,code,data,msg)ctx.body {code,data:dat…...
)
Android AMS——创建APP进程(五)
接上一篇,在 ActivityTaskSupervisor 中会判断进程是否存在,如果进程不存在,则会创建进程,执行 startProcessAsync() 方法。如果进程存在,则执行 realStartActivityLocked() 方法。在APP 的启动时,进程是不存在的。所以我们先来分析一下进程不存在的情况。 一、创建进程…...
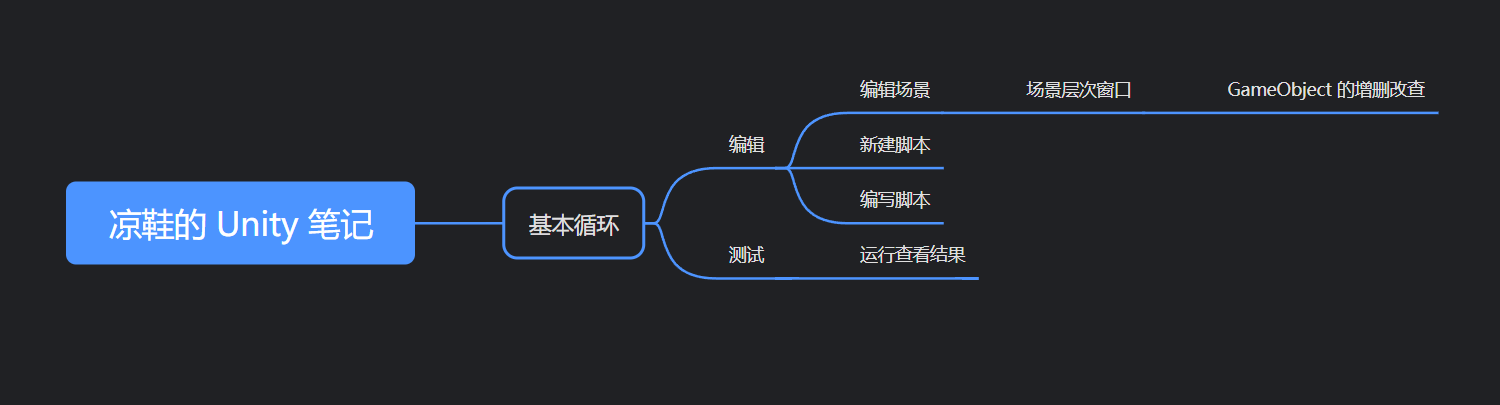
凉鞋的 Unity 笔记 102. 场景层次 与 GameObject 的增删改查
102. 场景层次 与 GameObject 的增删改查 在上一篇,我们完成了 Unity 引擎的 Hello world 输出,并且完成了第一个基本循环: 通过这次基本循环的完成,我们获得了一点点的 Unity 使用经验,这非常重要。 有实践经验后再…...
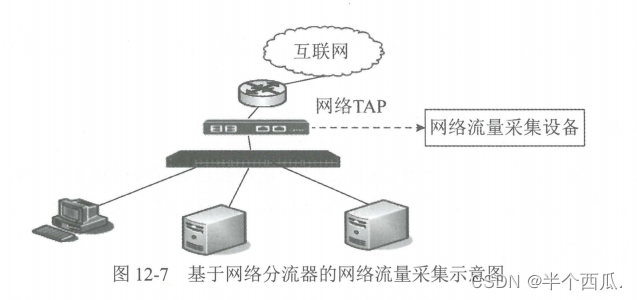
信息安全:网络安全审计技术原理与应用.
信息安全:网络安全审计技术原理与应用. 网络安全审计是指对网络信息系统的安全相关活动信息进行获取、记录、存储、分析和利用的工作。网络安全审计的作用在于建立“事后“安全保障措施,保存网络安全事件及行为信息,为网络安全事件分析提供线…...

嵌入式Linux应用开发-第十三章APP怎么读取按键值
嵌入式Linux应用开发-第十三章读取按键及按键驱动程序 第十三章 APP怎么读取按键值13.1 妈妈怎么知道孩子醒了13.2 APP读取按键的4种方法13.2.1 查询方式13.2.2 休眠-唤醒方式13.2.3 poll方式13.2.4 异步通知方式13.2.4.1 异步通知的原理:发信号13.2.4.2 应用程序之…...

Web 中间件怎么玩?
本次主要是聊聊关于 web 中间件, 分为如下四个方面 什么是 web 框架中间件 为什么要使用 web 中间件 如何使用及其原理 哪些场景需要使用中间件 开门见山 web 中间件是啥 Web 框架中的中间件主要指的是在 web 请求到具体路由之前或者之后,会经过一个或…...
)
HMTL知识点系列(4)
目录 1. 在你过去的项目中,你如何解决HTML的布局和样式问题?2. 你能否解释一下HTML的“文档对象模型”(DOM)是什么,以及它的重要性?3. 你有没有经验处理网页的兼容性问题,特别是在不同浏览器之间…...

CFS内网穿透靶场实战
一、简介 不久前做过的靶场。 通过复现CFS三层穿透靶场,让我对漏洞的利用,各种工具的使用以及横向穿透技术有了更深的理解。 一开始nmap探测ip端口,直接用thinkphpv5版本漏洞工具反弹shell,接着利用蚁剑对服务器直接进行控制,留下…...
【RabbitMQ实战】07 3分钟部署一个RabbitMQ集群
一、集群的安装部署 我们还是利用docker来安装RabbitMQ集群。3分钟安装一个集群,开始。 前提条件,docker安装了docker-compose。如果没安装的话,参考这里 docker-compose文件参考bitnami官网:https://github.com/bitnami/contai…...
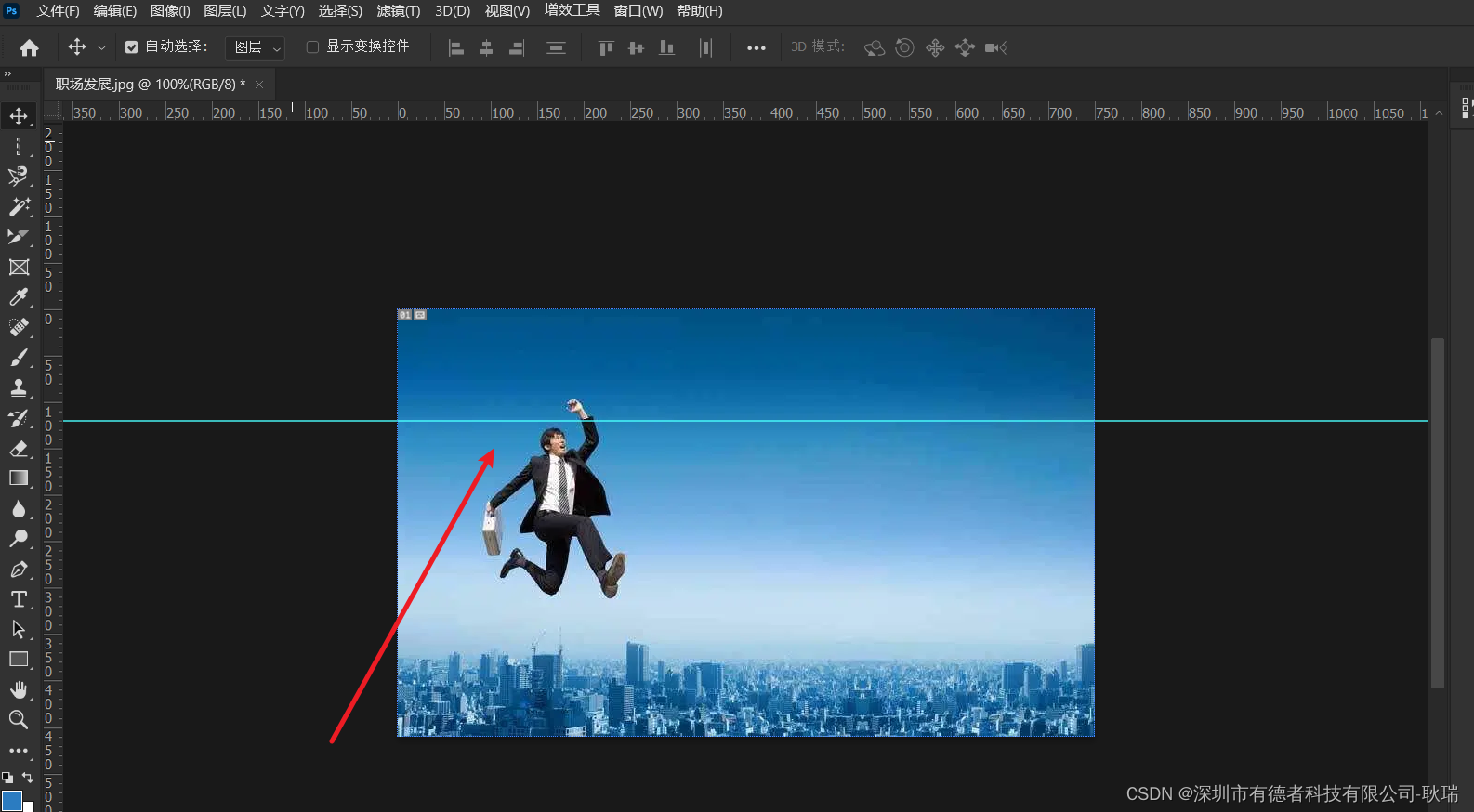
PS 切片工具 选择切片 切片存储
上文 PS 透视裁剪工具 中 我们简单讲述了透视裁剪工具 今天 我们来讲他后面的切片工具 首先 他的用途还是很多的 例如 你有一个很大的图片 其中包括 轮播 导航 主题内容 但他们都在一个图片上 你就可以用切片工具 将完整的图片切成多个部分 这里 我们选择了切片工具 光标也会…...

Git版本控制系统
概念: 一个免费的 开源 分布式源码仓库,帮助团队维护代码 个人使用 多人联机使用 git安装: 这里直接看大佬的安装 文章 很不错的 git 安装配置https://blog.csdn.net/mukes/article/details/115693833 安装完毕之后: 使用命名git -v查看…...
Element UI搭建首页导航和左侧菜单以及Mock.js和(组件通信)总线的运用
目录 前言 一、Mock.js简介及使用 1.Mock.js简介 1.1.什么是Mock.js 1.2.Mock.js的两大特性 1.3.Mock.js使用的优势 1.4.Mock.js的基本用法 1.5.Mock.js与前端框架的集成 2.Mock.js的使用 2.1安装Mock.js 2.2.引入mockjs 2.3.mockjs使用 2.3.1.定义测试数据文件 2…...
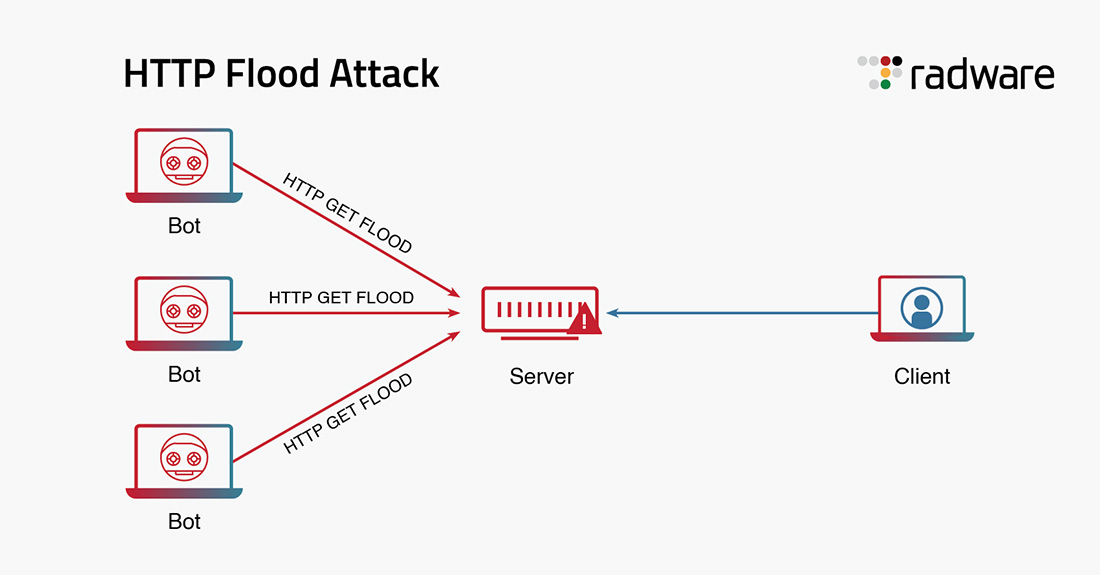
What is an HTTP Flood DDoS attack?
HTTP 洪水攻击是一种针对 Web 和应用程序服务器的第 7 层分布式拒绝服务 (DDoS) 攻击。HTTP 洪水攻击通过使用 HTTP GET 或 HTTP POST 请求执行 DDoS 攻击。这些请求是有效的,并且针对可用资源,因此很难防范 HTTP 洪水攻击。 匿名…...
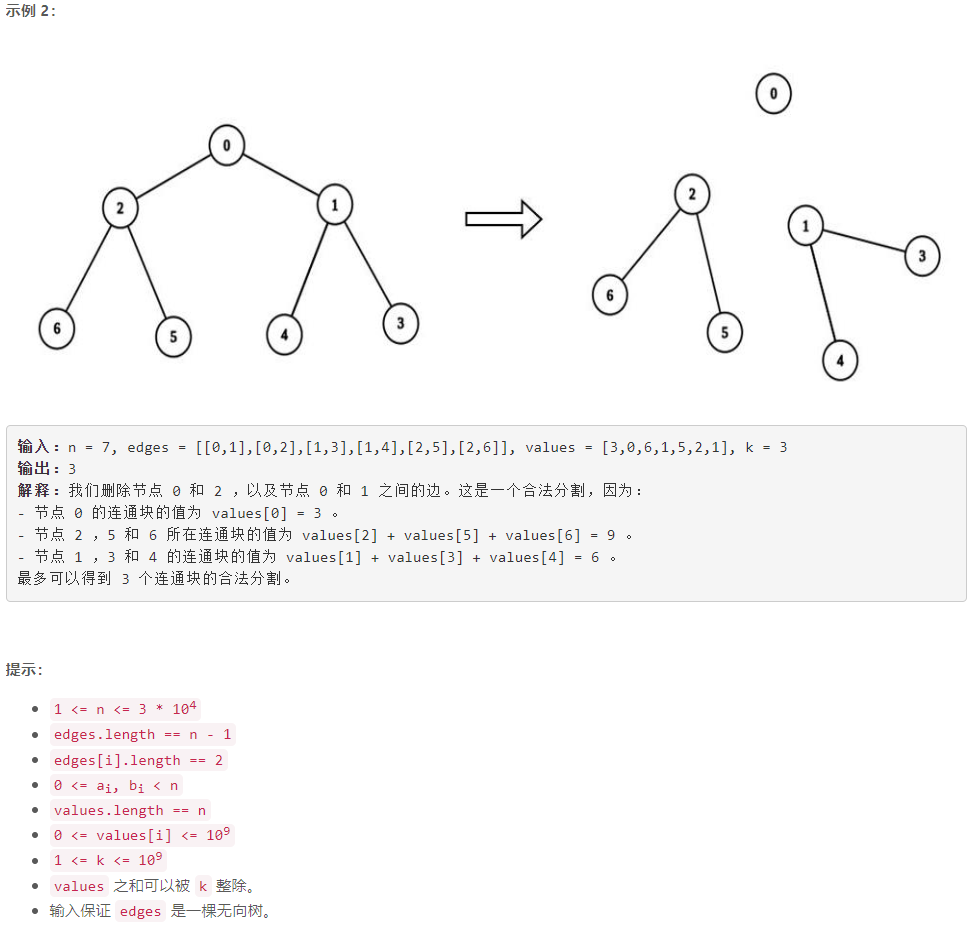
第 114 场 LeetCode 双周赛题解
A 收集元素的最少操作次数 模拟: 反序遍历数组,用一个集合存当前遍历过的不超过 k k k 的正数 class Solution { public:int minOperations(vector<int> &nums, int k) {unordered_set<int> vis;int n nums.size();int i n - 1;for (;; i--) {if…...

[Java框架] Java常用爬虫框架推荐
Selenium GitHub 截止 2023年9月份 Star数量27.7K Selenium是一款基于浏览器自动化的工具,它可以模拟用户在浏览器上的操作行为,并获取网页上的内容。Selenium支持多种浏览器,可以很好地处理JavaScript生成内容。但是Selenium相较于其他框架而…...
Kafka:安装与简单使用
文章目录 下载安装windows安装目录结构启动服务器创建主题发送一些消息启动消费者设置多代理集群常见问题 工具kafka tool 常用指令topic查看topic删除topic 常见问题参考文献 下载安装 下载地址:kafka-download windows安装 下载完后,找一个目录解压…...
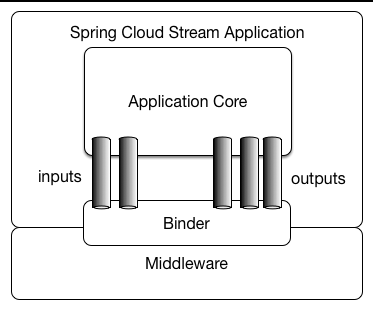
029-从零搭建微服务-消息队列(一)
写在最前 如果这个项目让你有所收获,记得 Star 关注哦,这对我是非常不错的鼓励与支持。 源码地址(后端):mingyue: 🎉 基于 Spring Boot、Spring Cloud & Alibaba 的分布式微服务架构基础服务中心 源…...

Python2020年06月Python二级 -- 编程题解析
题目一 数字转汉字 用户输入一个1~9(包含1和9)之间的任一数字,程序输出对应的汉字。 如输入2,程序输出“二”。可重复查询。 答案: 方法一 list1[一,二,三,四,五,六,七,八,九] while True:n int(input(请输入1~9之间任意一个数字…...
差分放大器的精髓:放大差模信号 抑制共模信号
参考如图基本的差分放大电路,在R1R2 R3R4的条件下,其输出与输入的关系为 : 具体推导过程参考:差分运算放大器的放大倍数的计算及结论_正在黑化的KS的博客-CSDN博客 由这个式子我们可以发现,差分放大器放大的是同相端与…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
