数据结构 图 并查集 遍历方法 最短路径算法 最小生成树算法 简易代码实现
文章目录
- 前言
- 并查集
- 图
- 遍历方法
- 广度优先遍历
- 深度优先遍历
- 最小生成树算法
- Kruskal算法
- Prim算法
- 最短路径算法
- Dijkstra算法
- BellmanFord算法
- FloydWarshall算法
- 全部代码链接
前言
- 图是真的难,即使这些我都学过一遍,再看还是要顺一下过程;
- 说明方式按照 概念-> 实现思想 -> 代码逻辑 —> 代码 的方式进行 ;
- 图片多来自于《算法导论》 等书 ;
- 后续可能会做更详细的补充
并查集
概念:
并查集(Disjoint Set)是一种用于处理集合合并与查询问题的数据结构。它主要支持两种操作:合并(Union)和查找(Find)。
在并查集中,每个元素都被看作一个节点,多个节点组成一个集合。每个集合通过一个代表元素来表示,通常选择集合中的某个元素作为代表元素。
合并操作将两个不相交的集合合并成一个集合,即将其中一个集合的代表元素指向另一个集合的代表元素。
查找操作用于确定某个元素所属的集合,即找到该元素所在集合的代表元素。
通过这两种操作,可以高效地判断两个元素是否属于同一个集合,以及将不相交的集合合并成一个集合。
实现逻辑:
- 下标代表节点
- 下标内的值为负代表为根节点
- 根节点的绝对值为该树的总节点个数
- 下标内的值为正值,代表的是其父亲节点的下标
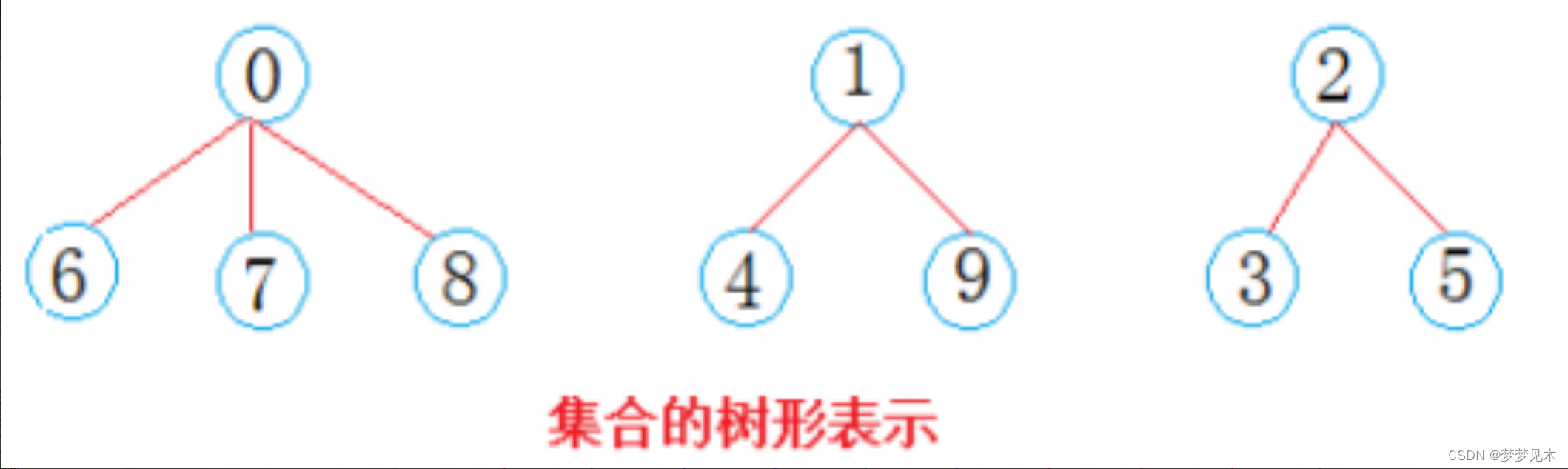

实现代码:
// 并查集代码
#include <vector>class DisiointSetUnion
{
private:std::vector<int> _set; public://数组下标本身就是存储的内容//DSU为用一维数组抽象的森林(可含多棵树)//默认 -1 表示默认全为单独的根节点DisiointSetUnion(int size):_set(size, -1){}//找到根节点下标size_t FindRoot(int x){// 根节点存储负值,且负值的绝对值为该树节点的数量;// 如果不为根节点,返回其父亲节点的下标;while (_set[x] >= 0){x = _set[x];}// 如果要压缩路径可在该函数内部添加后续方法return x; }void Union(int x1, int x2){int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (root1 != root2){_set[root1] += _set[root2];_set[ root2 ] = root1;}}//判断两节点是否一颗树中bool InSet(int x1, int x2){int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (root1 == root2){return true;}else{return false;}}//计算有几个树// 通过计算负值数size_t SetCount(){size_t count = 0 ;for (size_t i = 0; i < _set.size(); i++){if (_set[i] < 0){count++;}}return count; }};
图
基本概念:
节点(Vertex):也称为顶点,表示图中的元素。节点可以有附加的属性,如权重、颜色等。
边(Edge):表示节点之间的连接关系。边可以是有向的(有方向性)或无向的(无方向性)。有向边由起始节点指向目标节点,无向边没有方向。
路径(Path):是由边连接的节点序列。路径的长度是指路径上边的数量。
环(Cycle):是一条起始节点和终止节点相同的路径。
连通图(Connected Graph):如果图中任意两个节点之间都存在路径,则称该图为连通图。
子图(Subgraph):由图中一部分节点和边组成的图。
权重(Weight):边可以有权重,表示节点之间的关联程度或距离。
入度(In-degree)和出度(Out-degree):对于有向图,入度表示指向该节点的边的数量,出度表示从该节点出发的边的数量。
邻接点(Adjacent Vertex):与给定节点直接相连的节点
实现逻辑:
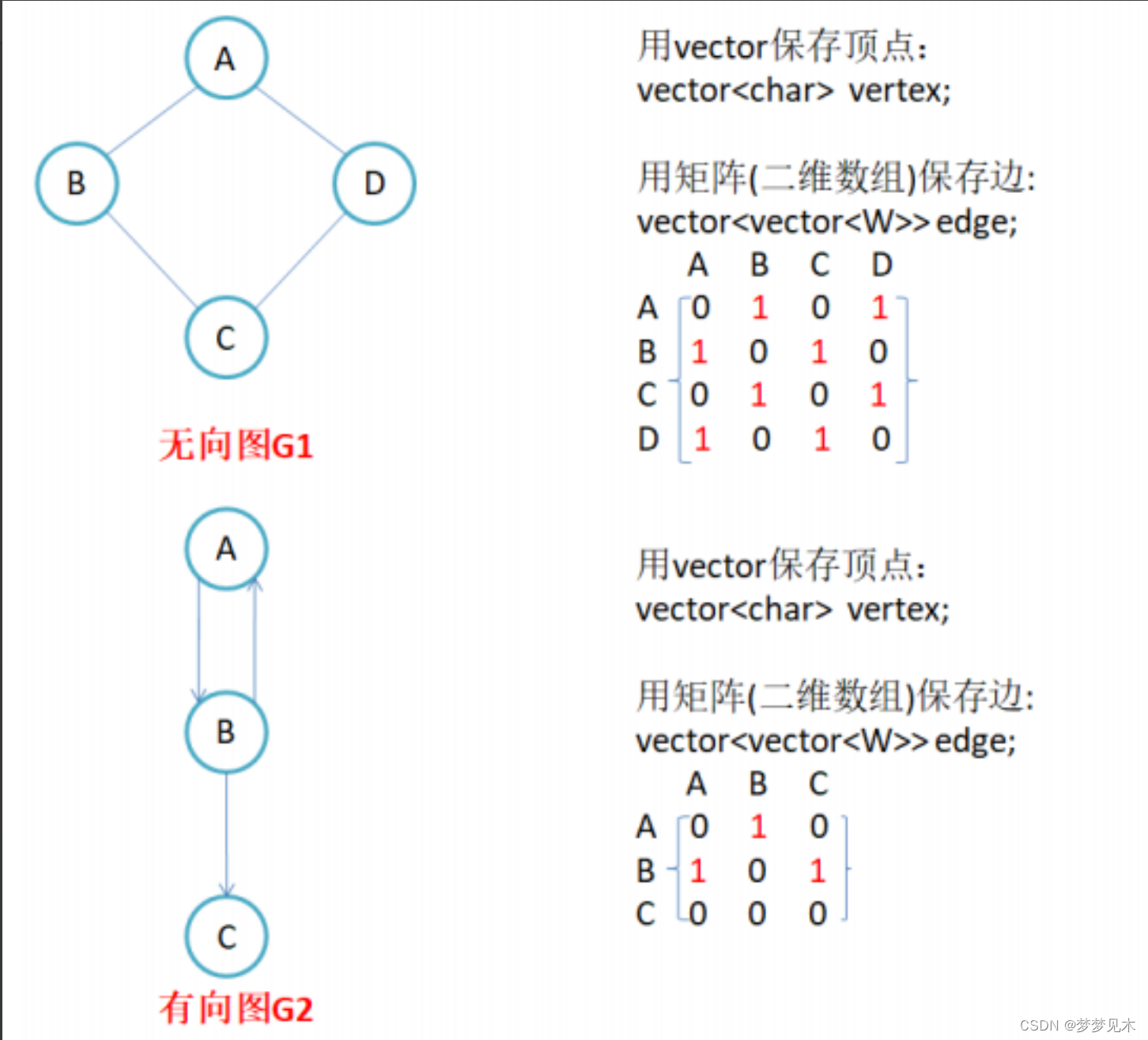
代码实现:
//邻接矩阵实现图//Direction为是否为有向图的标志位//INT_MAX为不存在的边的标识值// V 为顶点名类型 template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>class Graph{private: //成员变量map<V, size_t> _vIndexMap; // 存储顶点名与顶点在数组中的下标 顶点名->数组中下标vector<V> _vertexs; // 存储顶点 下标—>数组名vector<vector<W>> _matrix; // 图 //临界矩阵 // 此中建立边的关系public: //类内类//类内定义类,Edge类是Graph类的友元struct Edge{size_t _srci; // 在有向图时,为出发顶点size_t _dsti; // 在有向图时,为目的顶点W _w; //权重Edge(size_t srci, size_t dsti, const W& w):_srci(srci), _dsti(dsti), _w(w){}bool operator<(const Edge& eg){return _w < eg._w;}bool operator>(const Edge& eg){return _w > eg._w;}};public: // 成员方法 typedef Graph<V, W, MAX_W, Direction> Self;Graph() = default;//只初始化节点,没有边Graph(const V* vertexs, size_t n){_vertexs.reserve(n);// 对_vIndexMap 、 _vertexs 初始化for (size_t i = 0; i < n; ++i){_vertexs.push_back(vertexs[i]);_vIndexMap[vertexs[i]] = i;}// 对 _matrix 初始化_matrix.resize(n);for (auto& e : _matrix){e.resize(n, MAX_W);}}// 根据顶点名查找下标size_t GetVertexIndex(const V& v){auto ret = _vIndexMap.find(v);if (ret != _vIndexMap.end()){return ret->second;}else{printf(" 查找顶点不存在\n");return -1;}}// 添加边,被AddEdge函数调用void _AddEdge(size_t srci, size_t dsti, const W& w){//发生了越界错误 //代码的逻辑有问题 ? ? ? ? ? _matrix[srci][dsti] = w;if (Direction == false){_matrix[dsti][srci] = w;}}// 调用_AddEdge函数添加边void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetVertexIndex(src);size_t dsti = GetVertexIndex(dst);_AddEdge(srci, dsti, w);}}
遍历方法
广度优先遍历
实现逻辑:
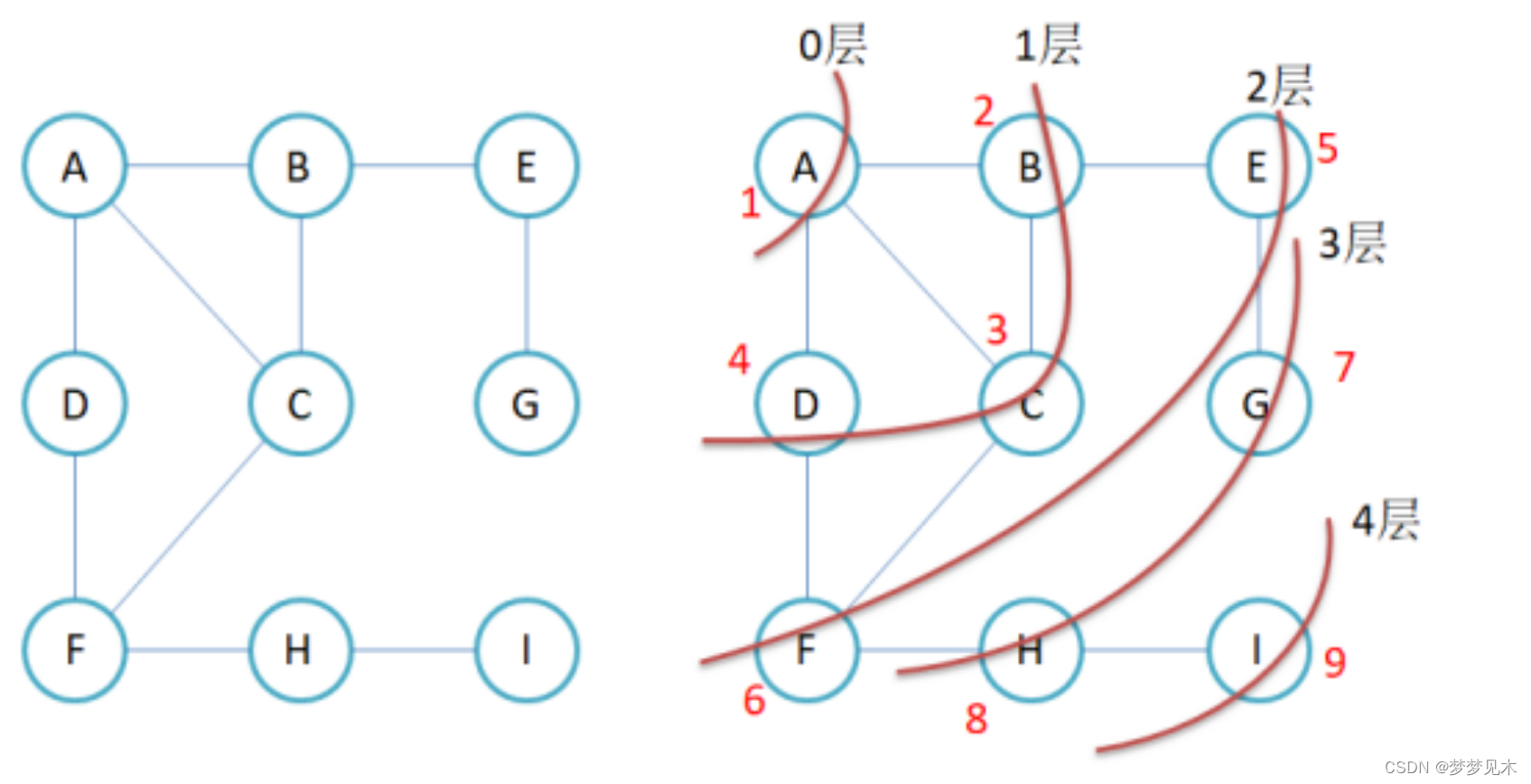
代码逻辑:
代码实现:
//测试运行成功!//如果为不完全连通的图怎么办???//src 为遍历的起始顶点//广度优先遍历//利用 队列 + 标记数组void BFS(const V& src){size_t srcindex = GetVertexIndex(src);vector<bool> visted;visted.resize(_vertexs.size(), false);// true代表已经被遍历过//队列的作用类似与二叉树层序遍历中队列的作用queue<int> q;q.push(srcindex);visted[srcindex] = true;size_t d = 1; //代表广度遍历的层数 size_t dSize = 1; //队列中剩余的顶点数while (!q.empty()){//只有当V为基础类型时,此行代码才通用 cout << src << "的" << d << "度的好友 ";while (dSize--){size_t front = q.front();q.pop();for (size_t i = 0; i < _matrix.size(); i++){if (visted[i] == false && _matrix[front][i] != MAX_W){只有当V为基础类型时,此行代码才通用cout << "[" << i << ":" << _vertexs[i] << "]";visted[i] = true;q.push(i);}}}cout << endl;dSize = q.size();d++;}cout << endl;}
深度优先遍历
实现逻辑:
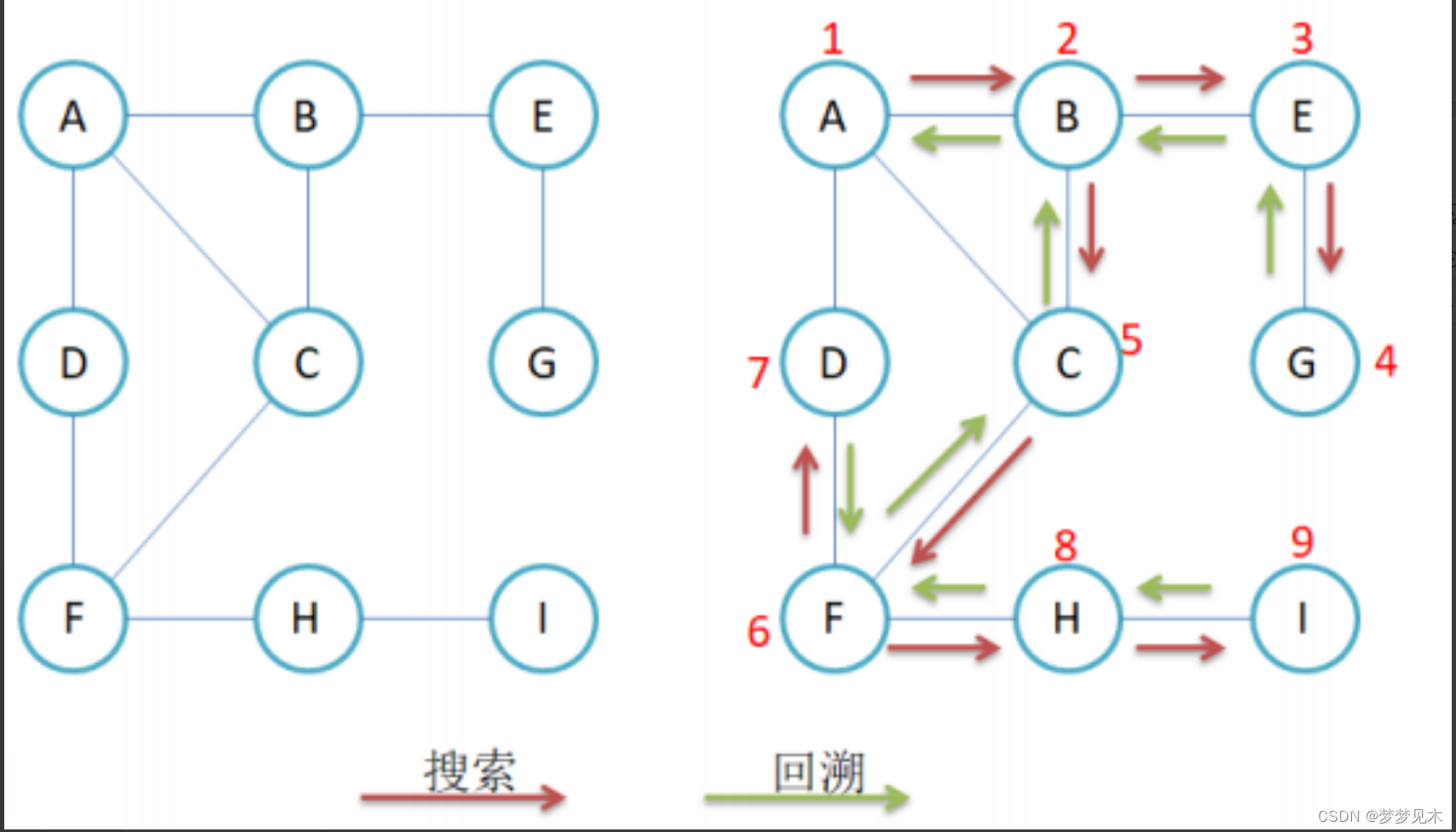
代码实现:
//测试成功!// 递归实现 //思想也是类似与二叉树的递归遍历//深度优先遍历void DFS(const V& src){size_t srcindex = GetVertexIndex(src);vector<bool> visted;visted.resize(_vertexs.size(), false);_DFS(srcindex, visted);}//可以遍历不连通的树吗? //visited用于标志是否已经遍历过//深度优先遍历辅助函数void _DFS(size_t srcIndex, vector<bool>& visited){cout << "[" << srcIndex << _vertexs[srcIndex] << "]";visited[srcIndex] = true;for (size_t i = 0; i < _vertexs.size(); i++){if (visited[i] == false && _matrix[srcIndex][i] != MAX_W){_DFS(i, visited);}}}
最小生成树算法
概念:
最小生成树(Minimum Spanning Tree,简称MST)是一种在连通无向图中生成一棵树的算法,使得这棵树包含了图中的所有节点,并且边的权重之和最小。
最小生成树的特点是,它是一个无环的连通子图,其中包含了图中的所有节点,并且边的权重之和最小。
Kruskal算法
概念:
Kruskal算法:Kruskal算法是一种贪心算法,它按照边的权重从小到大的顺序逐步选择边,如果选择某条边不会形成环,则将该边加入到最小生成树中,直到最小生成树中包含了所有的节点。
实现逻辑:
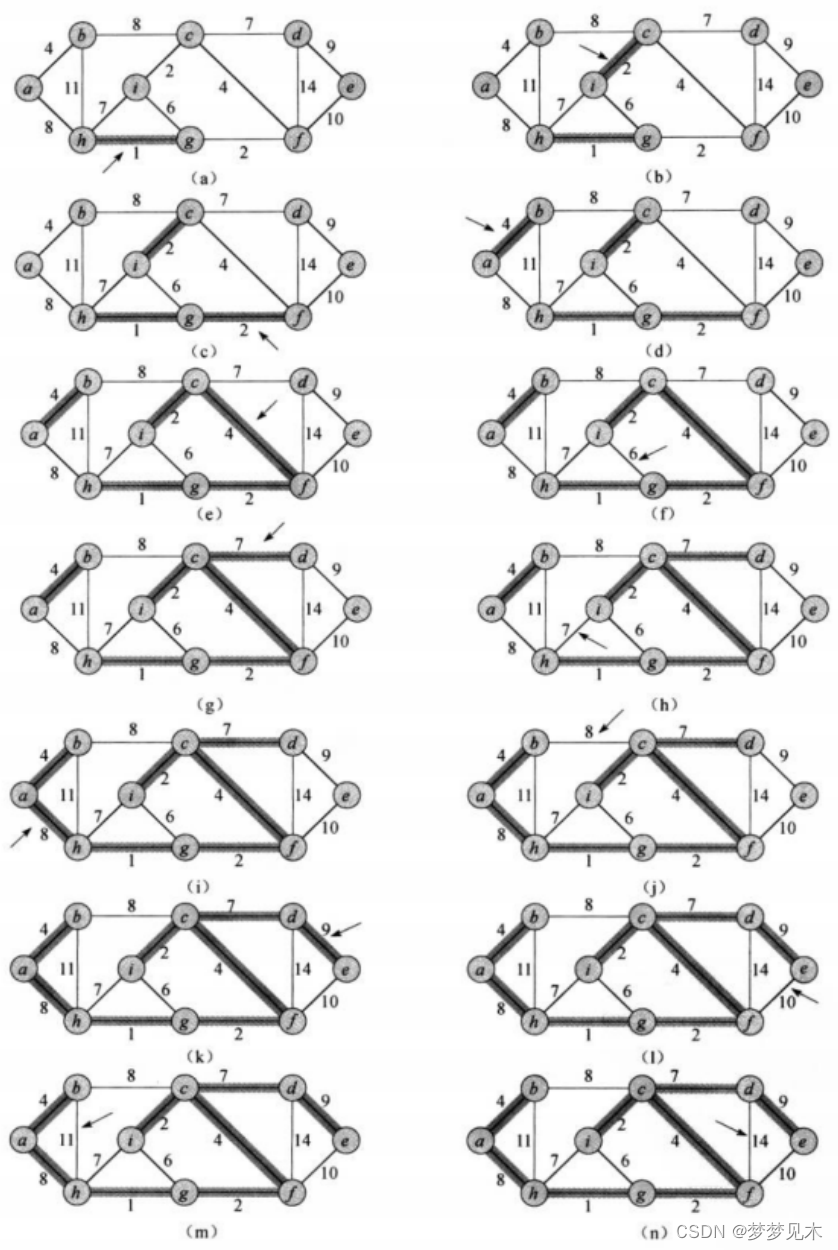
代码实现:
// Kruskal算法寻找最小生成树// 最小生成树是在已存在的连通图上找到把所有点连起来且总权重最小的N-1条边(N为节点总数)// 每次先找最小边再经判断是否构成回路确定是否连接顶点// 判断是否构成回路用并查集?// 贪心算法,寻找局部最优解 W Kruskal(Self& minTree){size_t n = _vertexs.size();minTree._vertexs = _vertexs;minTree._vIndexMap = _vIndexMap;minTree._matrix.resize(n); // 注意深浅拷贝for (size_t i = 0; i < n; i++){//! ! ! ! !minTree._matrix[i].resize(n, MAX_W);}//创建一个堆,用来快速找出最小路径priority_queue<Edge, vector<Edge>, Mygreater> minque;for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){//i < j 这个条件的原因是: 生成最小生成树的依据原图为无向图//最小生成树本身也是无向的if (i < j && _matrix[i][j] != MAX_W){minque.push(Edge(i, j, _matrix[i][j]));}}}//开始选边 + 判是否成环int size = 0; // 计算是否满足 N - 1条边的条件W total = W(); // 计算生成的最小生成树的总权重 并查集类对象DisiointSetUnion dsf(n);while (!minque.empty()){Edge min = minque.top();minque.pop();if (!dsf.InSet(min._dsti, min._srci)){cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;minTree._AddEdge(min._srci, min._dsti, min._w);dsf.Union(min._srci, min._dsti);size++;total += min._w;}else{// 构成了环cout << "成环:" << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;}}if (size == n - 1){return total;}else{return W();}}
Prim算法
概念:Prim算法:Prim算法也是一种贪心算法,它从一个起始节点开始,逐步选择与当前最小生成树相邻的边中权重最小的边,并将其加入到最小生成树中,直到最小生成树中包含了所有的节点。
实现逻辑: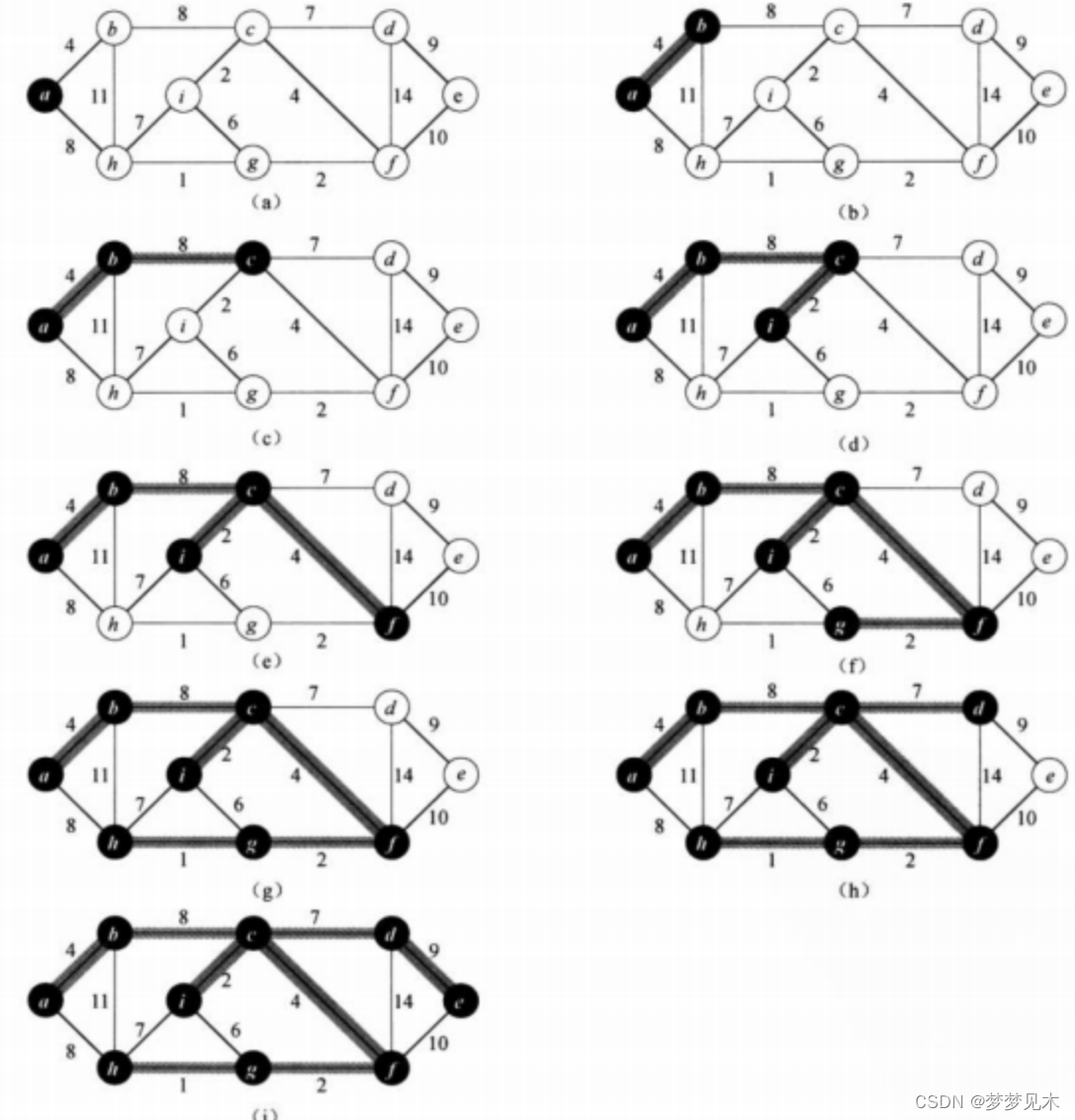
代码实现:
//Prim算法寻找最小生成树//src为生成最小生成树的起始点W Prim(Self& minTree, const V& src){size_t srci = GetVertexIndex(src); // 不是给顶点名找下标的函数么…… // ! ! ! ! ! !size_t n = _vertexs.size(); minTree._vertexs = _vertexs ;minTree._vIndexMap = _vIndexMap; minTree._matrix.resize(n);for (size_t i = 0; i < n; i++){minTree._matrix[i].resize(n, MAX_W);}// 记录是否已经被连接//为什么要有两个?vector<bool> X(n, false);vector<bool> Y(n, true);X[srci] = true; Y[srci] = false;priority_queue<Edge, vector<Edge>, Mygreater> minq;for (size_t i = 0; i < n; i++){if (_matrix[srci][i] != MAX_W){minq.push(Edge(srci, i, _matrix[srci][i]));}}//开始选边size_t size = 0;W total = W();while (!minq.empty()){Edge min = minq.top();minq.pop();if (X[min._dsti]){//成环}else{minTree._AddEdge(min._srci, min._dsti, min._w);X[min._dsti] = true;Y[min._srci] = false;size++;total += min._w;if (size == n - 1){//最多n-1条路break;}for (int i = 0; i < n; i++){if (_matrix[min._dsti][i] != MAX_W && Y[i]) // ? ? ? Y[i]? ? ? {minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));}}}}if (size == n - 1){return total;}else{return W();}}
最短路径算法
概念:最短路径算法用于找到两个节点之间的最短路径,即路径上边的权重之和最小的路径。
Dijkstra算法
概念:
Dijkstra算法:Dijkstra算法是一种贪心算法,用于解决单源最短路径问题,即从一个给定的起始节点到图中所有其他节点的最短路径。算法维护一个距离数组,记录从起始节点到每个节点的当前最短距离。算法每次选择距离起始节点最近的未访问节点,并更新其邻接节点的最短距离。重复这个过程直到所有节点都被访问
注意:不可处理存在负权值的图
实现逻辑: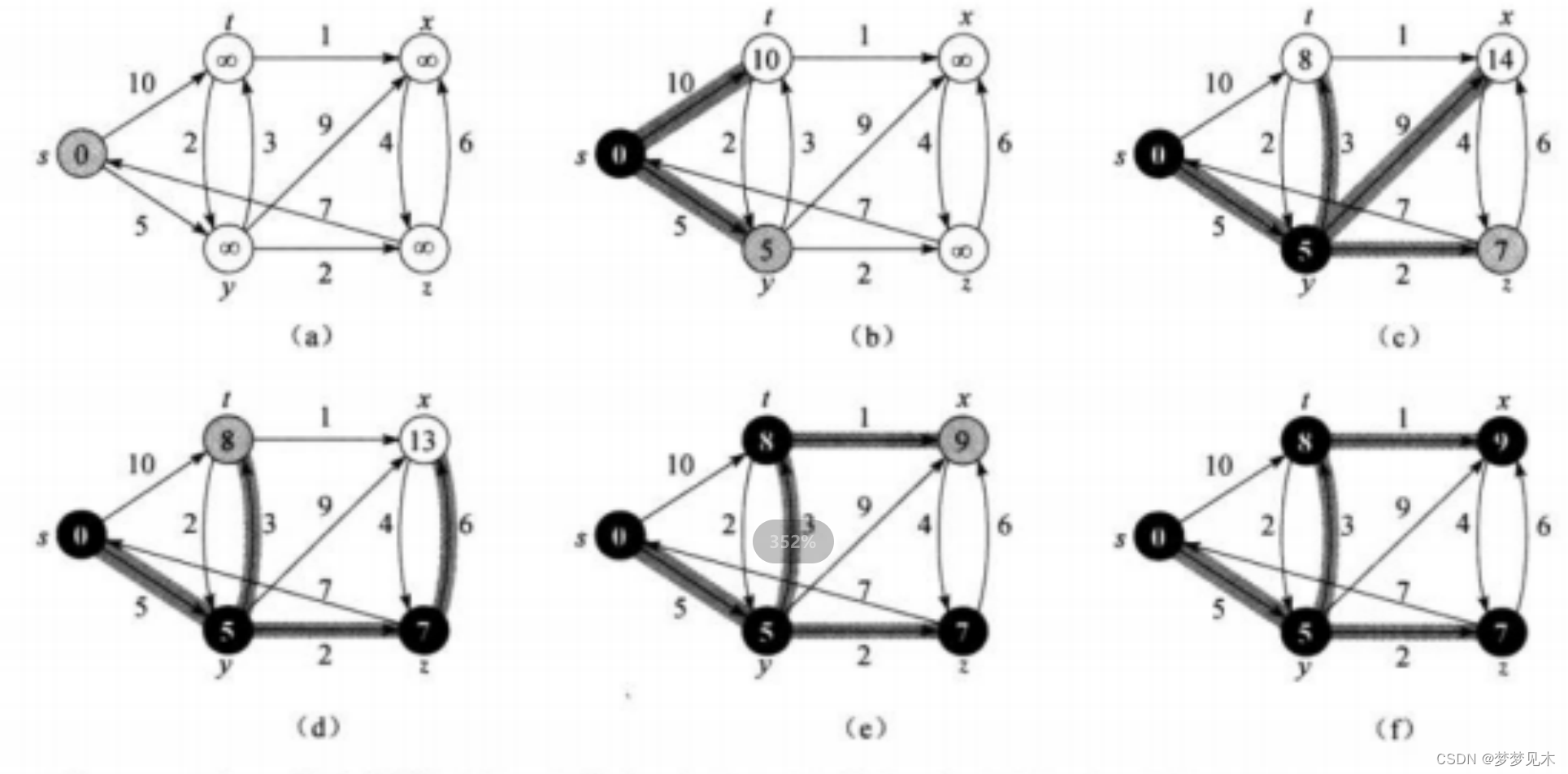
代码实现:
//时间复杂度为多少 ? ? ?// Dijkstra 不考虑负路径的问题,或者说无法处理父权值路径的图//Dijkstra 为最短路径算法//最短路径:即计算指定出发点到任意点的距离// dist 记录从出发点到该点的当前已更新的最短路径,注意是当前已更新的。 dist pPath 为输出参数void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath){size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();dist.resize(n, MAX_W);pPath.resize(n, -1);dist[srci] = 0;pPath[srci] = srci;// 已经确定的最短路径的集合// 满足什么条件确定最短路径不再更新 ? // 被置为true后就不会再更新吗 ? 是 vector<bool> S(n, false);for (size_t j = 0; j < n; j++){// 1. 找出起始点直接连接的最短路径节点和其对应的权重// 用于记录/更新最短路径和该最短路劲对应的权重int u = 0;W min = MAX_W;// size_t v的for循环更新后会影响该循环结束时u的值for (size_t i = 0; i < n; i++){if (S[i] == false && dist[i] < min){u = i;min = dist[i];}}// 已选的最短路径不会再选了 S[u] = true;for (size_t v = 0; v < n; v++){if (S[v] == false && _matrix[u][v] != MAX_W&& dist[u] + _matrix[u][v] < dist[v]) /* 关键 */{dist[v] = dist[u] + _matrix[u][v];pPath[v] = u; }}}}//不可用于打印FloydWarshall的结果//辅助打印最短路径结果void PrintShortPath(const V& src, vector<W>& dist, vector<int>& pPath){size_t srci = GetVertexIndex(src); size_t n = _vertexs.size();for (size_t i = 0; i < n; i++){size_t parent = pPath[i];cout << _vertexs[i] << "到起始顶点" << src <<"最小总权值为:" << dist[i] << "——最短路径为:";cout << _vertexs[i] << "<-";while (parent != srci){cout << _vertexs[parent] << "<-" ;parent = pPath[parent];}cout << src << endl;}}
BellmanFord算法
概念:
Bellman-Ford算法:Bellman-Ford算法是一种动态规划算法,用于解决单源最短路径问题,可以处理带有负权边的图。算法维护一个距离数组,记录从起始节点到每个节点的当前最短距离。算法通过对所有边进行松弛操作,即尝试通过更新路径来减小距离数组中的值。重复这个过程直到没有可以更新的路径或者存在负权环。
时间复杂度分析:
Dijkstra算法适用于没有负权边的图,时间复杂度为O(V^2)或O((V + E)logV),其中V是节点数,E是边数。Bellman-Ford算法适用于带有负权边的图,时间复杂度为O(VE),其中V是节点数,E是边数。
实现逻辑:
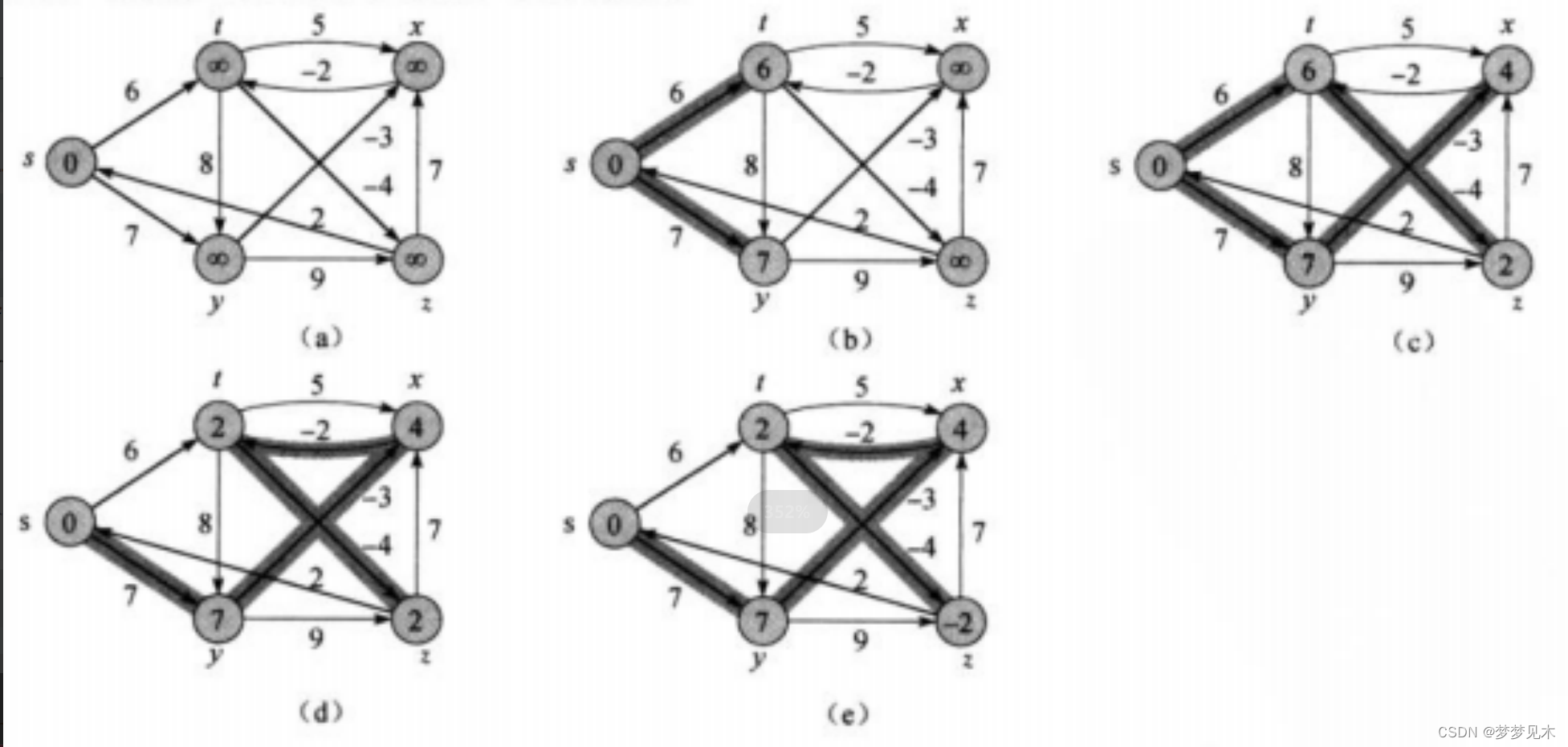
代码实现:
/ BellmanFord的时间复杂度为多少 ? 如何计算的 ?// BellmanFord可以处理负权值路径存在的场景 // 关于负权值环路的问题 : 不做考虑,这种情况就没有最小权值路径,权值延着负权值环路走会无限减小,直到负无穷大// BellmanFord和Dijkstra的区别在于无确认该点为最短路径的这一动作 ?;// 停止更新的条件: 1.是依据图的最大可更新次数停止更新 || 2.本次更新没有新的最短路径出现bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath){size_t n = _vertexs.size(); size_t srci = GetVertexIndex(src); dist.resize(n, MAX_W); pPath.resize(n, -1);// 更新出发顶点 srci 为缺省值(0)dist[srci] = W();// 最多更新n轮 , 因为极端情况为所有顶点排成一条线for (size_t k = 0; k < n; ++k){bool update = false;cout << "第" << k << "轮更新" << endl;for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){// 实际上这个判断还隐含了条件 dist[i] != MAX_W ! ! ! ! ! ! !// 因为这个隐含条件达到了类似广度优先向外遍历更新最短路径的效果if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j]){update = true;cout << _vertexs[i] << "->" << _vertexs[j] << ":" << _matrix[i][j] << endl;dist[j] = dist[i] + _matrix[i][j];pPath[j] = i;}}//? ? ? ? ? ? ? ?// 说明本次更新无新的最短路径出现,后续更新的结果也必是无效,故停止更新if (update == false){break; }}}// 判断是否存在负权回路 for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j]){cout << "存在负权回路" << endl;return false; }}}return true; }
FloydWarshall算法
Floyd-Warshall算法的基本思想是通过中间节点逐步更新节点对之间的最短路径。算法维护一个二维数组D,其中D[i][j]表示节点i到节点j的最短路径长度。算法的核心是使用三重循环,对于每一对节点(i, j)和每一个可能的中间节点k,尝试更新D[i][j]的值,即通过节点k来缩短节点i到节点j的路径长度。
算法的具体步骤如下:
-
初始化二维数组D,将所有节点对之间的距离初始化为无穷大,但将节点自身到自身的距离初始化为0。
-
对于每一个中间节点k,遍历所有的节点对(i, j),尝试更新D[i][j]的值。更新的方式是比较D[i][j]的当前值和D[i][k] + D[k][j]的和,将较小的值赋给D[i][j]。
-
重复步骤2,对于每一个中间节点k,直到所有的节点对都被考虑过。
-
最终得到的二维数组D中,D[i][j]表示节点i到节点j的最短路径长度。
Floyd-Warshall算法的时间复杂度为O(V^3),其中V是节点数。由于需要遍历所有的节点对和中间节点,因此算法在处理大规模图时的效率可能较低。但它的优点是能够同时计算出所有节点对之间的最短路径,适用于需要获取全局最短路径信息的场景,例如网络路由算法中的链路状态路由协议。
实现逻辑:

// FloydWarshall算法求最短路径// vvpPath 中的值的含义为 ? ? ? 中间节点 ? 如果不存在中间节点就是指原本直接相连的点 ? void FloydWarshall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath){size_t n = _vertexs.size(); // ????vvDist.resize(n);vvpPath.resize(n);// 初始化for (size_t i = 0; i < n ; i++ ){vvDist[i].resize(n, MAX_W);vvpPath[i].resize(n, -1);}// ? ? ? ? ? for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){if (_matrix[i][j] != MAX_W){vvDist[i][j] = _matrix[i][j]; vvpPath[i][j] = i;}if (i == j){vvDist[i][j] = W();}}}for (size_t k = 0; k < n; k++){for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){// k 为中间节点 !?if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W&& vvDist[i][k] + vvDist[k][j] < vvDist[k][j]){vvDist[i][j] = vvDist[i][k] + vvDist[k][j]; vvpPath[i][j] = vvpPath[k][j]; // ! ! ! ! !}}}//打印权值和路径for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){if (vvDist[i][j] == MAX_W){printf("%3c", '*');}else{printf("%3d", vvDist[i][j]);}}cout << endl; }cout << endl; for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){printf("%3d", vvpPath[i][j]);}cout << endl; }cout << "————————————————" << endl;}}
全部代码链接
代码链接——gitee
相关文章:

数据结构 图 并查集 遍历方法 最短路径算法 最小生成树算法 简易代码实现
文章目录 前言并查集图遍历方法广度优先遍历深度优先遍历 最小生成树算法Kruskal算法Prim算法 最短路径算法Dijkstra算法BellmanFord算法FloydWarshall算法 全部代码链接 前言 图是真的难,即使这些我都学过一遍,再看还是要顺一下过程;说明方…...
idea Springboot 教师标识管理系统开发mysql数据库web结构java编程计算机网页源码maven项目
一、源码特点 springboot 教师标识管理系统是一套完善的信息系统,结合springboot框架和bootstrap完成本系统,对理解JSP java编程开发语言有帮助系统采用springboot框架(MVC模式开发),系统 具有完整的源代码和数据库&…...
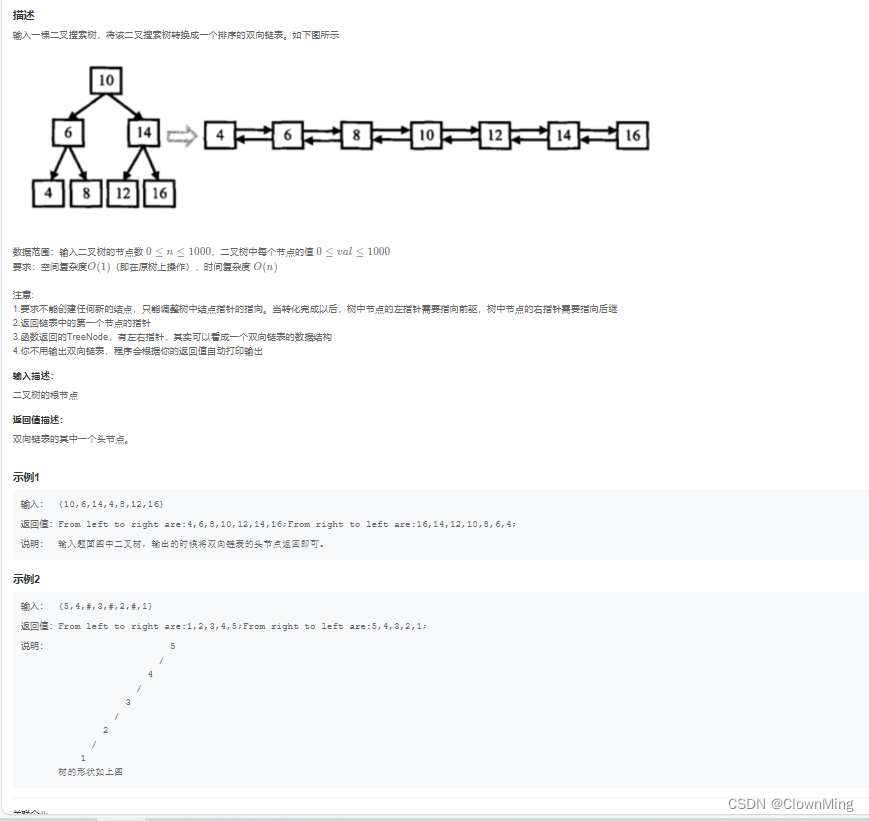
2023-9-30 JZ36 二叉搜索树与双向链表
题目链接:二叉搜索树与双向链表 import java.util.*; /** public class TreeNode {int val 0;TreeNode left null;TreeNode right null;public TreeNode(int val) {this.val val;}} */ public class Solution {TreeNode pre null;public TreeNode Convert(Tree…...
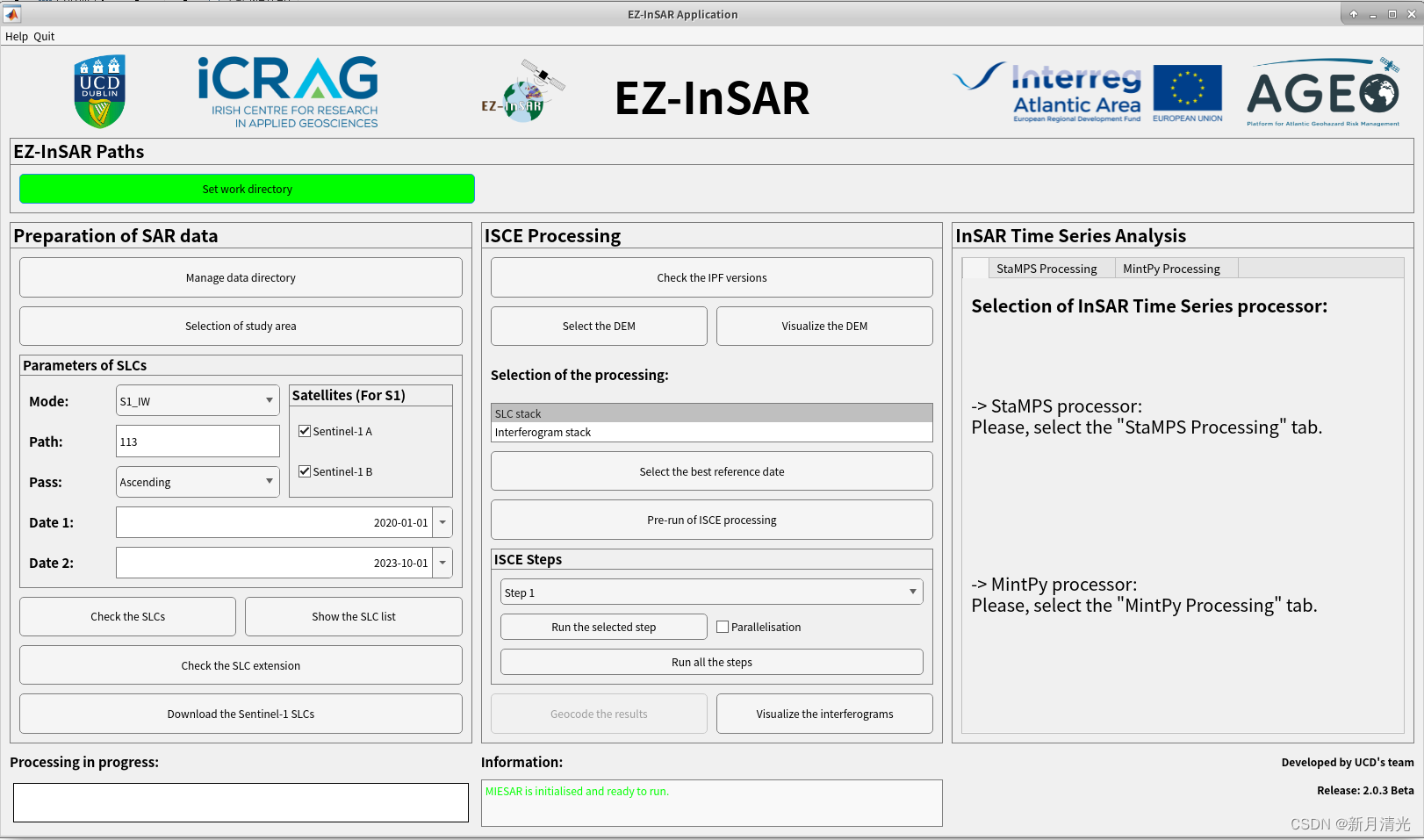
在windows的ubuntu LTS中安装及使用EZ-InSAR进行InSAR数据处理
EZ-InSAR(曾被称为MIESAR,即Matlab界面用于易于使用的合成孔径雷达干涉测量)是一个用MATLAB编写的工具箱,用于通过易于使用的图形用户界面(GUI)进行干涉合成孔径雷达(InSAR)数据处理…...
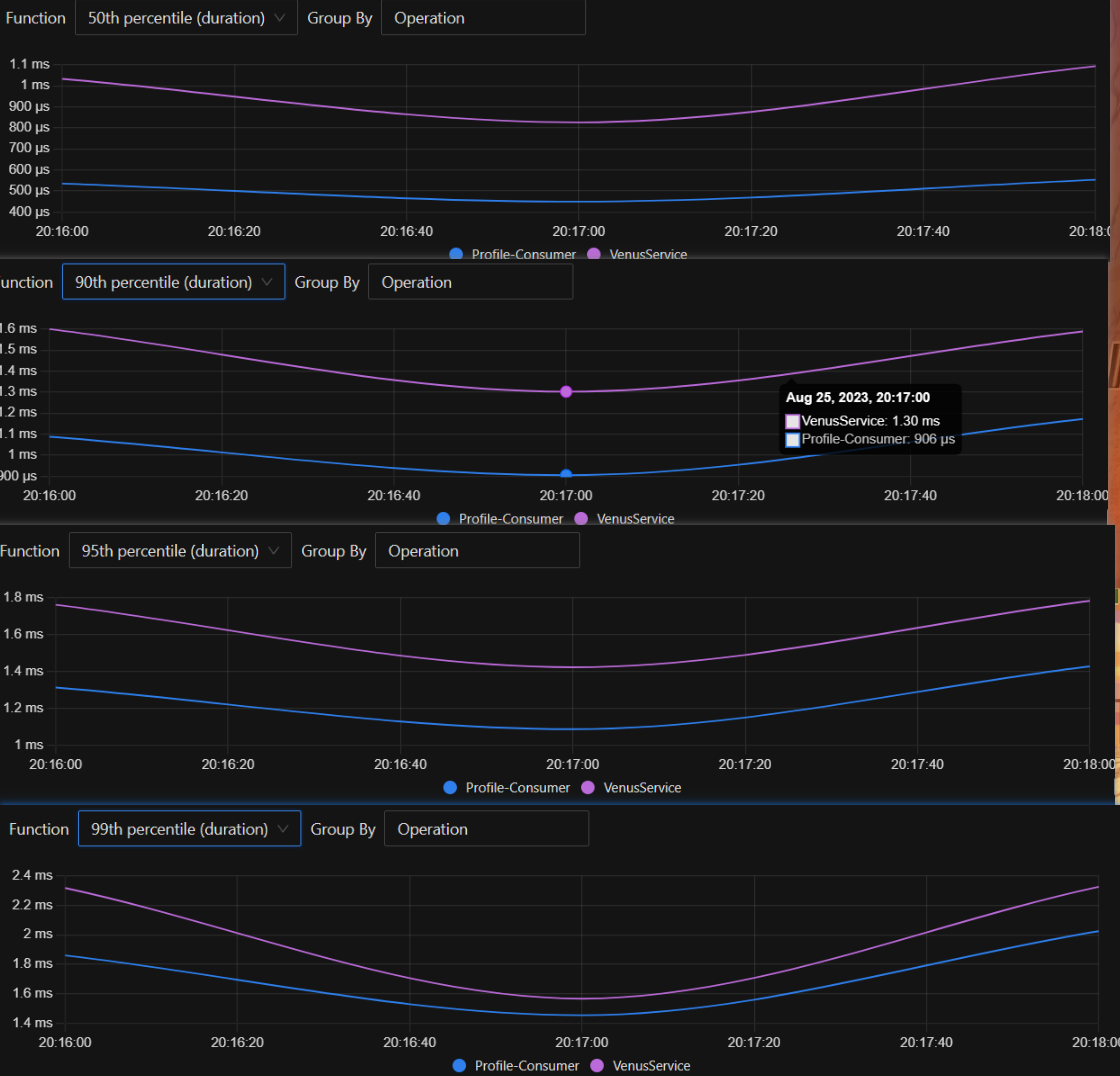
腾讯mini项目-【指标监控服务重构】2023-08-25
今日已办 traefik proxy jaeger Prometheus prometheus | Prometheus 配置完依然无法实现 web-url的前缀访问【待解决】 Set span storage type : elasticsearch services:elasticsearch:image: elasticsearch:7.17.12container_name: elasticsearchnetworks:- backend # …...
数据挖掘(1)概述
一、数据仓库和数据挖掘概述 1.1 数据仓库的产生 数据仓库与数据挖掘: 数据仓库和联机分析处理技术(存储)。数据挖掘:在大量的数据中心挖掘感兴趣的知识、规则、规律、模式、约束(分析)。数据仓库用于决策分析: 数据仓库:是在数…...
YApi Pro
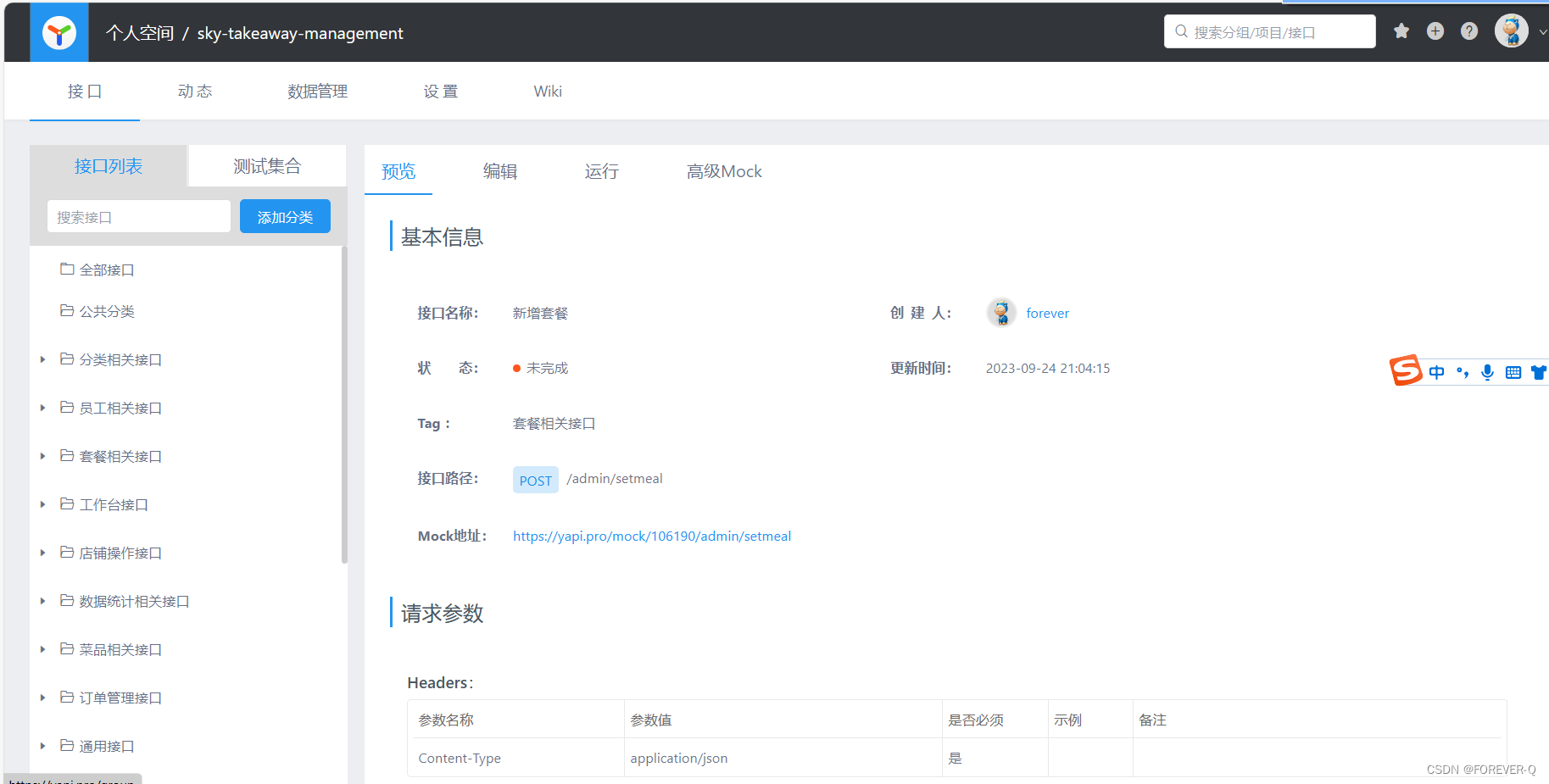
1.介绍 说明:YApi Pro 是一款高效、易用、功能强大的 API 管理平台,旨在为开发、产品、测试人员提供更优雅的接口管理服务。它可以帮助开发者轻松创建、发布、维护 API,同时为用户提供了优秀的交互体验,开发人员可以更加高效地完…...
AUTOSAR RTE介绍(更新版230925)
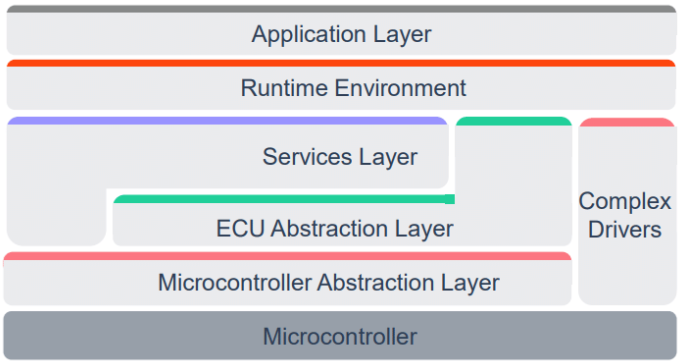
RTE是什么 AUTOSAR RTE(Run Time Environment)实现了AUTOSAR系统中的虚拟功能总线(VFB),提供了SWC(Software Component)之间的访问接口和SWC对于BSW资源的访问接口。RTE为SWC中的Runnable提供与其他SWC或者BSW模块通信的接口,RTE将Runnable映射到OS Task中,并且管理Runna…...

深度学习笔记_1、定义神经网络
1、使用了PyTorch的nn.Module类来定义神经网络模型;使用nn.Linear来创建全连接层。(CPU) import torch.nn as nn import torch.nn.functional as F from torchsummary import summary# 定义神经网络模型 class Net(nn.Module):def __init__(self):super(Net, self).__init__()…...

【Java 进阶篇】MySQL 事务详解
在数据库管理中,事务是一组SQL语句的执行单元,它们被视为一个整体。事务的主要目标是保持数据库的一致性和完整性,即要么所有SQL语句都成功执行,要么所有SQL语句都不执行。在MySQL中,事务起到了非常重要的作用…...
自动装配与注解开发)
Spring修炼之旅(3)自动装配与注解开发
一、自动装配说明 1.1概述 自动装配是使用spring满足bean依赖的一种方法 spring会在应用上下文中为某个bean寻找其依赖的bean。 1.2装配机制 Spring中bean有三种装配机制,分别是: 在xml中显式配置; 在java中显式配置; 隐式…...
嵌入式Linux应用开发-基础知识-第十六章GPIO和Pinctrl子系统的使用
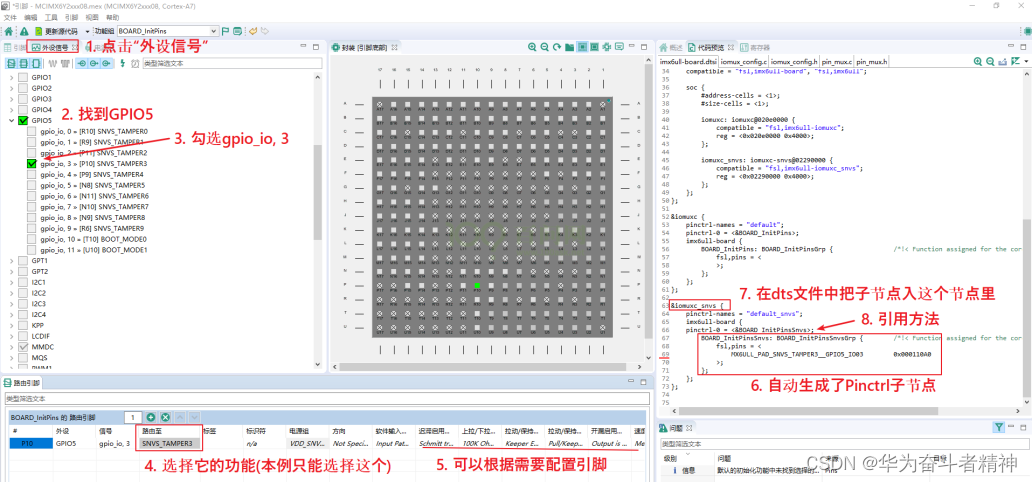
嵌入式Linux应用开发-基础知识-第十六章GPIO和Pinctrl子系统的使用 第十六章 GPIO 和 Pinctrl 子系统的使用16.1 Pinctrl 子系统重要概念16.1.1 引入16.1.2 重要概念16.1.3 示例16.1.4 代码中怎么引用pinctrl 16.2 GPIO子系统重要概念16.2.1 引入16.2.2 在设备树中指定引脚16.2…...

Ubuntu系统下使用apt-get安装Mysql8
记录一下在Ubuntu20.04 64位系统下面使用apt-get方式安装mysql8关系型数据库 Centos下使用yum安装Mysql8(Mysql5.7)以及常见的配置和使用 首先肯定是检查下当前Ubuntu系统是否已经安装过mysql数据库 一般拿到新的云服务器是没有安装的 rootmyw:~# whe…...
jenkins联动显示或隐藏参数
1. 添加组件 Active Choices Plug-in 如jenkins无法联网,可在以下两个地址中下载插件,然后放到/home/jenkins/.jenkins/plugin下面重启jenkins即可 Active Choices Active Choices | Jenkins plugin 2. 效果如下: sharding为空时…...
Error: Activity class {xxx.java} does not exist
git切换到不同的branch之后,报下面的错误: Error: Activity class {xxx.java} does not exist 解决方案: 首先clean 然后会删除build目录 然后点击:Invalidate Caches Android Studio重启,然后重新build即可。...

保护模式阶段测试-模拟3环0环调用
保护模式阶段测试-模拟3环0环调用 最近又复习了一下保护模式相关的内容,然后打算搞个能够把段页的大部分知识能够串联起来的测试代码 最终想到的一个项目如下: 三环部分: 0.编写一个函数读取高2g的地址内容 1.通过设备通信到0环告诉0环我新…...

Dart笔记:stream_channel 包用法
标题1 标题2 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/133426961 【介绍】stream_channel是一个用…...

Java进阶必会JVM-深入浅出Java虚拟机
系列文章目录 送书第一期 《用户画像:平台构建与业务实践》 送书活动之抽奖工具的打造 《获取博客评论用户抽取幸运中奖者》 送书第二期 《Spring Cloud Alibaba核心技术与实战案例》 送书第三期 《深入浅出Java虚拟机》 文章目录 系列文章目录前言一、推荐书籍二…...

1200*B. Sorted Adjacent Differences(构造)
Problem - 1339B - Codeforces 解析: 题目要求每相邻两个值差的绝对值相等或递增。 先排序,可以想到我们先取两侧的数肯定相距最远,然后靠中心每次取两个数,这样符合题目要求。 直接遍历,先取的是答案靠后的数据&…...

恼人的TCP套接字部分发送成功场景
源起 以前就知道套接字有可能出现部分发送成功的可能,直到近段时间一个典型的使用场景触发了明确的此问题,才予以重视,比较深入地考虑解决这个问题的方案! 分析 因为TCP的流式特征,如果出现部分发送成功,…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...
