【数据结构】外部排序、多路平衡归并与败者树、置换-选择排序(生成初始归并段)、最佳归并树算法
目录
1、外部排序
1.1 基本概念
1.2 方法
2、多路平衡归并与败者树
2.1 K路平衡归并
2.2 败者树
3、置换-选择排序(生成初始归并段)编辑
4、最佳归并树
4.1 理论基础编辑
4.2 构造方法 编辑
5、各种排序算法的性质
1、外部排序
1.1 基本概念
外部排序是指对大规模数据进行排序,其中无法将整个数据集一次性加载到内存中。因此需要将数据划分为适当大小的块,然后对每个块进行排序。在此之后,将这些排好序的块合并成更大的块,直到最终得到一个已排序的数据集。
外部排序是一种常见的数据处理技术,适用于需要对大量数据进行排序的场景,例如处理大型数据库或处理大型文件。通常采用归并排序算法来实现外部排序,其核心思想是将多个有序的子序列合并成一个有序的序列,以减少排序的时间和空间复杂度。
在外部排序中,需要考虑如何对数据进行分块、如何将块排序以及如何将排好序的块进行合并。为了提高排序效率,还需要考虑如何优化输入和输出数据的读取和写入。
1.2 方法
外部排序是一种处理超过内存容量的数据的排序方法。以下是外部排序的几种常见方法:
-
归并排序:将大文件分成若干个小文件,排序这些小文件,再进行归并排序,将小文件合并成一个有序的大文件。
-
快速排序:将大文件分割成若干个小文件,对这些小文件进行快速排序,然后将排序好的小文件合并成一个有序的大文件。
-
堆排序:利用堆的结构对数据进行排序,可以将大文件分成若干个小文件,将小文件中的数据建成堆,然后再进行堆排序。
-
多路归并排序:将大文件划分成多个子文件,每个子文件都小于内存容量,然后对于每个子文件,将其分成多个块,将每个块读入内存进行排序,最后进行多路归并。
-
分块排序:将大文件划分为若干个块,每个块都可以在内存中排序,然后将每个块中的数据合并成一个有序的文件。
这些方法都可以通过将大文件分割成小文件或块来解决内存容量不足的问题,并利用多路归并等技术来进行排序。
例子:
假设我们有一个文件,其中包含 1000 万个整数,需要对其进行排序。然而,计算机的内存只能容纳 1000 个整数,因此我们需要将该文件分成 10000 个大小为 1000 的块。
接下来,我们将这些块读取到内存中,对每个块进行排序,然后将它们写回磁盘。这是称为"归并排序"的过程。在每个块中进行排序的好处是可以优化内存中的使用,而且在每个块中进行的排序比在整个文件上进行的排序更快。
接下来,我们将排好序的 10000 个块合并成一个大的有序文件。为了合并这些块,我们可以使用归并排序的原理。我们将前两个块合并成一个块,再将第三个块与已合并的块合并,以此类推,直到所有块都被合并成一个大块。
最后,我们将这个大块写回磁盘,即得到了完全排好序的文件。这个过程可能会涉及到多次读取和写入磁盘,但是外部排序的好处是可以处理非常大的文件,而不需要太多的内存。
2、多路平衡归并与败者树
2.1 K路平衡归并
K路平衡归并是一种归并排序的变体,它将一个大文件分成K个子文件并对每个子文件进行排序,然后将它们合并成一个大文件。它的主要目的是在内存有限的情况下对大型数据集进行排序。
K路平衡归并的基本思想是将输入文件分成K份,每份放入磁盘上的一个块中,然后针对每个块进行排序。排序后,每个块中的第一个元素被放入一个最小堆或多个最小堆中,堆的大小为K。从堆中选择最小元素,将其放入输出缓冲区中,并且从所属块的下一个元素中选择一个元素来取代刚刚被放入输出缓冲区的元素。重复此过程,直到所有输入文件中的元素都被放入输出缓冲区中。输出缓冲区的元素可以按顺序写入输出文件。
K路平衡归并的时间复杂度为O(n log n),其中n表示输入文件的大小。它需要的额外空间取决于K和块的大小,通常情况下可以控制在几兆字节的范围内。
2.2 败者树
败者树是一种用于外部排序的数据结构,它基于树形结构,常用于对大量数据进行排序,尤其是当内存无法容纳所有待排序数据时。败者树的思想在于通过比较已排序的子序列中最小的元素来确定最终的排序顺序。
在败者树中,首先构建一棵初始的完全二叉树,其中每个节点存储一个元素。初始时,将每个需要排序的子序列的第一个元素放入这棵二叉树的最底层叶子节点。接下来,从叶子节点开始向上进行比较,每次比较两个叶子节点中的较小值,并将较小值向其父节点传递。这样,最终得到的顶部节点就是已排序的所有元素中的最小值。
在外部排序中,每次从磁盘中读取一定数量的数据块并进行排序,然后将每个数据块的最小值放入败者树中,以确定整体排序的顺序。当一个数据块中的所有元素都已被取出并放入败者树中时,将从该数据块中读取下一个元素,直到整个排序过程结束。
败者树的主要优点是它只需要常数级别的额外内存空间,并且可以对任意大小的数据集进行排序。它的主要缺点在于实现比较复杂,需要一定的算法知识和技巧。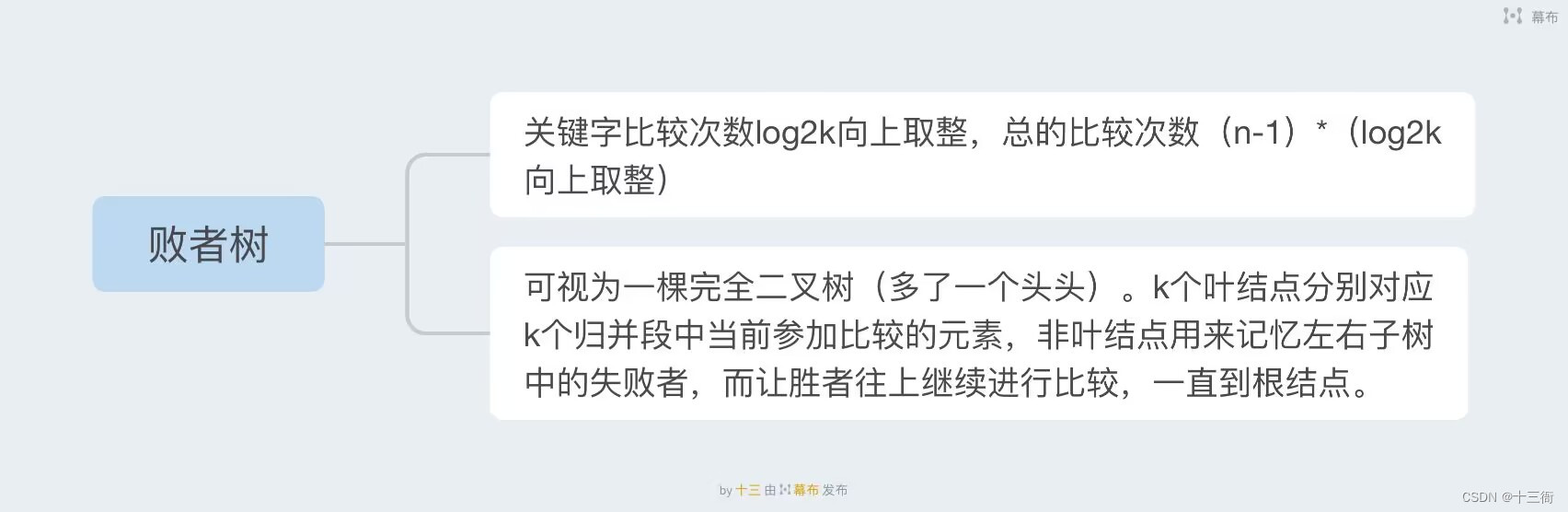
3、置换-选择排序(生成初始归并段)
4、最佳归并树
4.1 理论基础
4.2 构造方法 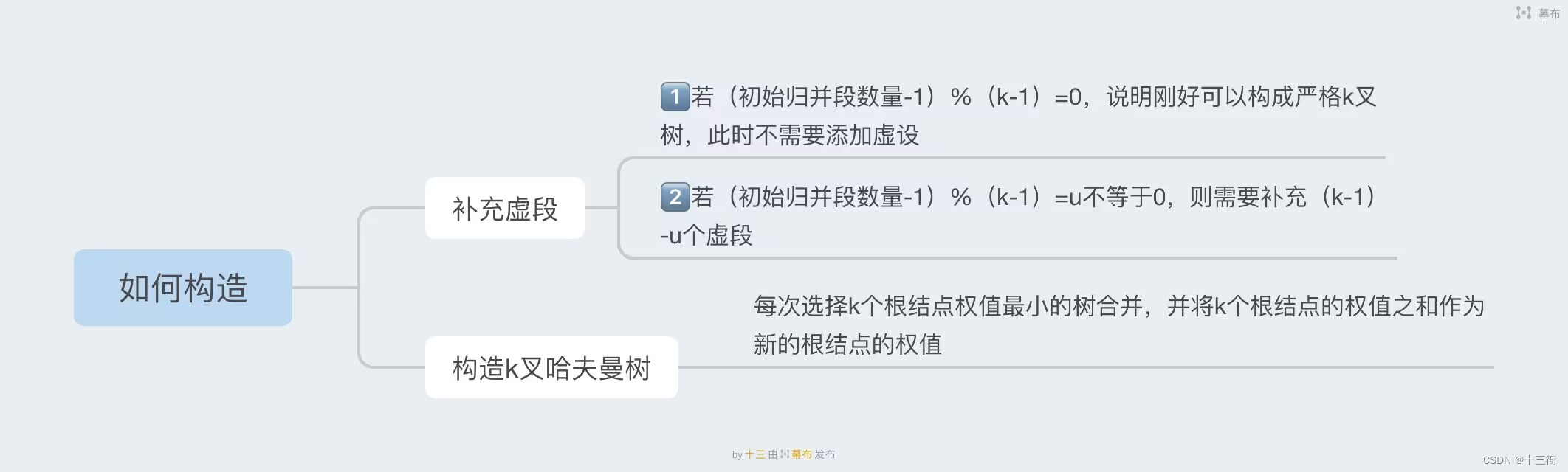
5、各种排序算法的性质
1. 冒泡排序:稳定,平均时间复杂度O(n^2);
2. 选择排序:不稳定,平均时间复杂度O(n^2);
3. 插入排序:稳定,平均时间复杂度O(n^2);
4. 快速排序:不稳定,平均时间复杂度O(nlogn);
5. 归并排序:稳定,平均时间复杂度O(nlogn);
6. 堆排序:不稳定,平均时间复杂度O(nlogn);
7. 希尔排序:不稳定,平均时间复杂度O(nlogn);
8. 基数排序:稳定,平均时间复杂度O(d(n+k)),其中d是数字的最大位数。
稳定性指的是排序后相同元素之间的相对位置是否改变;时间复杂度指的是排序算法在最坏情况下的时间复杂度。
相关文章:

【数据结构】外部排序、多路平衡归并与败者树、置换-选择排序(生成初始归并段)、最佳归并树算法
目录 1、外部排序 1.1 基本概念 1.2 方法 2、多路平衡归并与败者树 2.1 K路平衡归并 2.2 败者树 3、置换-选择排序(生成初始归并段)编辑 4、最佳归并树 4.1 理论基础编辑 4.2 构造方法 编辑 5、各种排序算法的性质 1、外部排序 1.1 基本概…...

抽象工厂模式 创建性模式之五
在看这篇文章之前,请先看看“简单工厂模式”和“工厂方法模式”这两篇博文,会更有助于理解。我们现在已经知道,简单工厂模式就是用一个简单工厂去创建多个产品,工厂方法模式是每一个具体的工厂只生产一个具体的产品,然…...

servlet如何获取PUT和DELETE请求的参数
1. servlet为何不能获取PUT和DELETE请求的参数 Servlet的规范是POST的数据需要转给request.getParameter*()方法,没有规定PUT和DELETE请求也这么做 The Servlet spec requires form data to be available for HTTP POST but not for HTTP PUT or PATCH requests. T…...
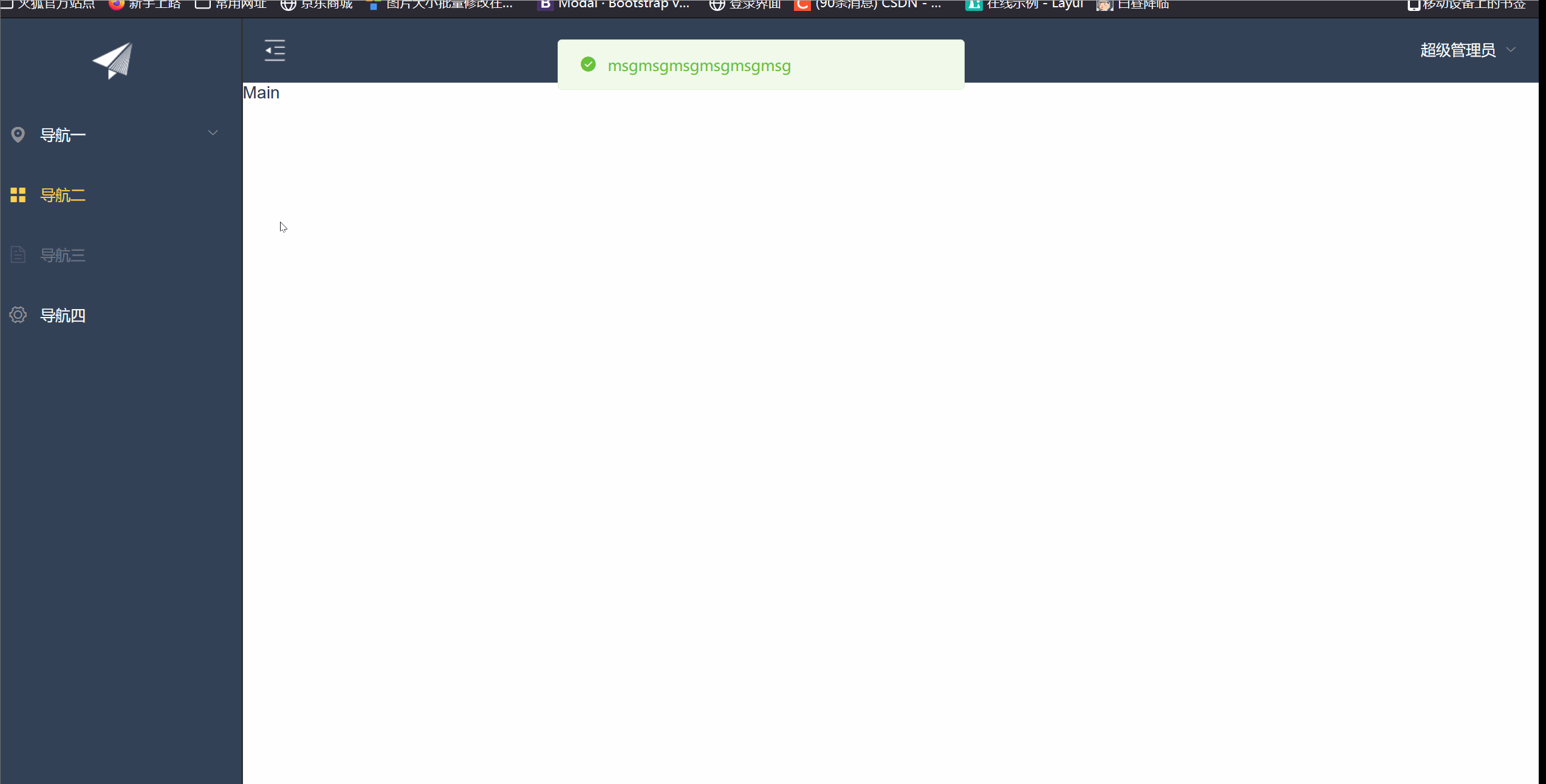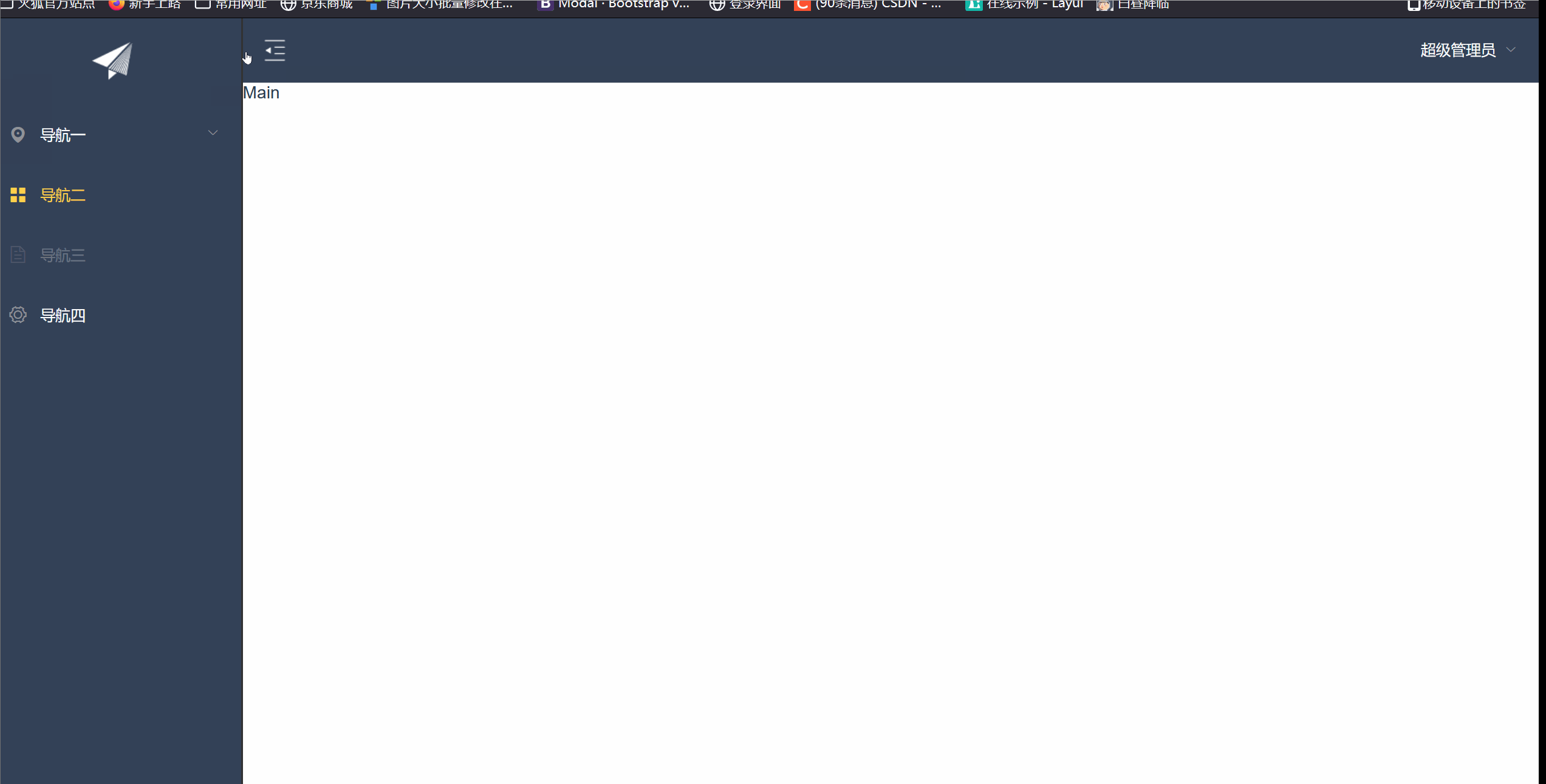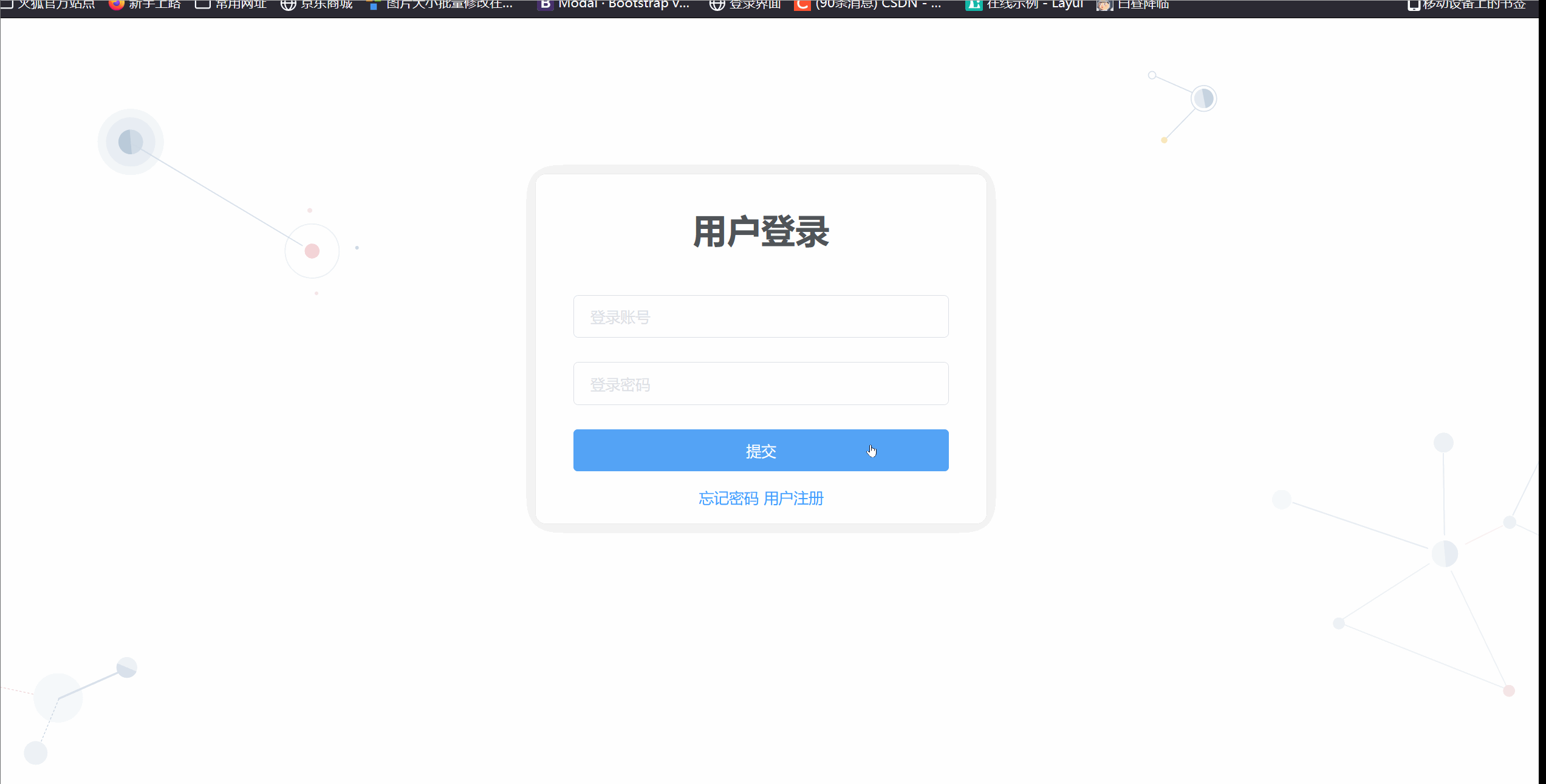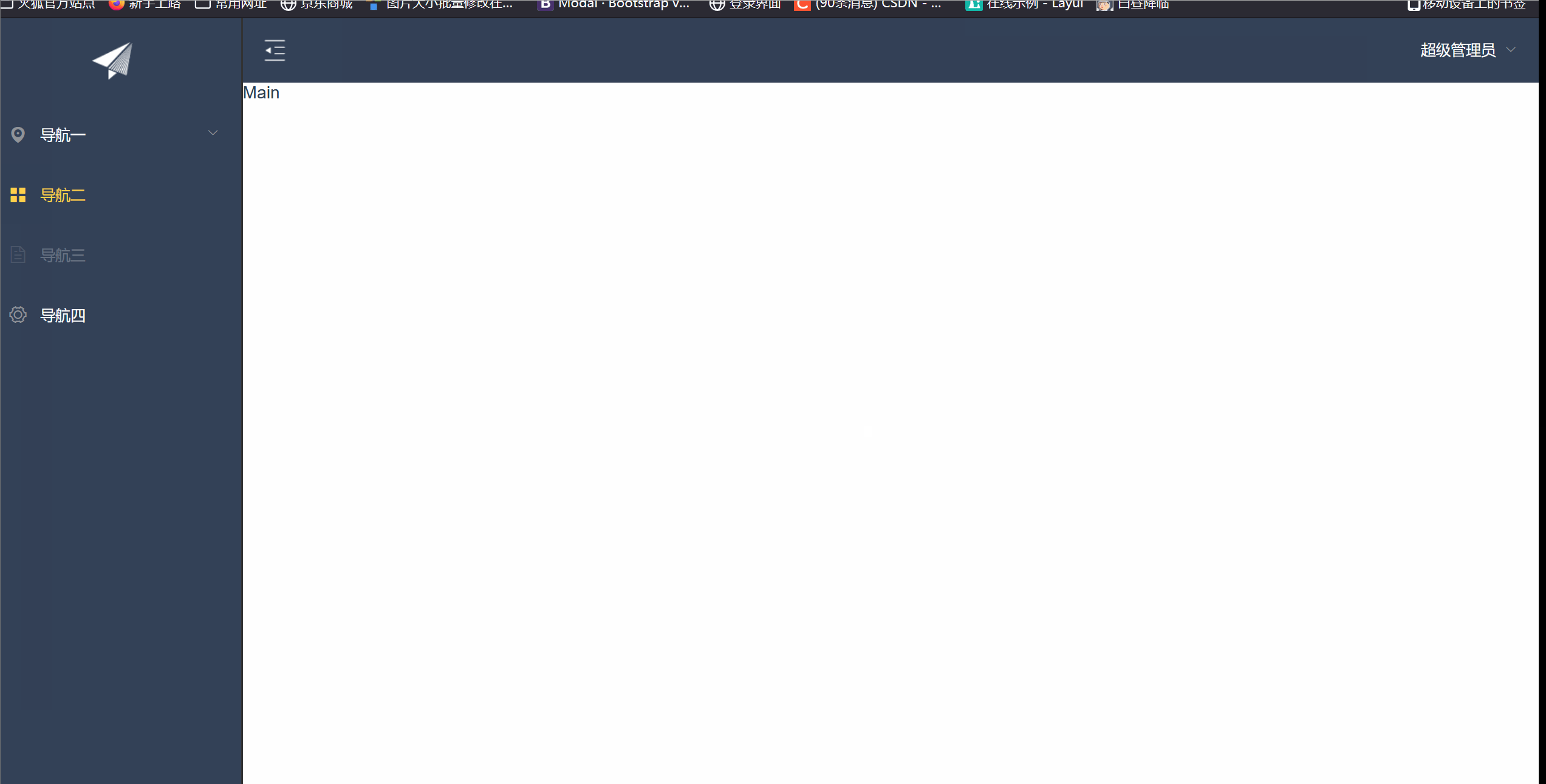
【Vue.js】使用Element中的Mock.js搭建首页导航左侧菜单---【超高级教学】
一,Mock.js 1.1 认识Mock.js Mock.js是一个用于前端开发中生成随机数据、模拟接口响应的 JavaScript 库。模拟数据的生成器,用来帮助前端调试开发、进行前后端的原型分离以及用来提高自动化测试效率 总结来说,Element中的Mock.js是一个用于…...

从技术创新到应用实践,百度智能云发起大模型平台应用开发挑战赛!
大模型已经成为未来技术发展方向的重大变革,热度之下更需去虚向实,让技术走进产业场景。在这样的背景下,百度智能云于近期发起了“百度智能云千帆大模型平台应用开发挑战赛”。 挖掘大模型落地应用 千帆大模型平台应用开发挑战赛启动 在不久前…...
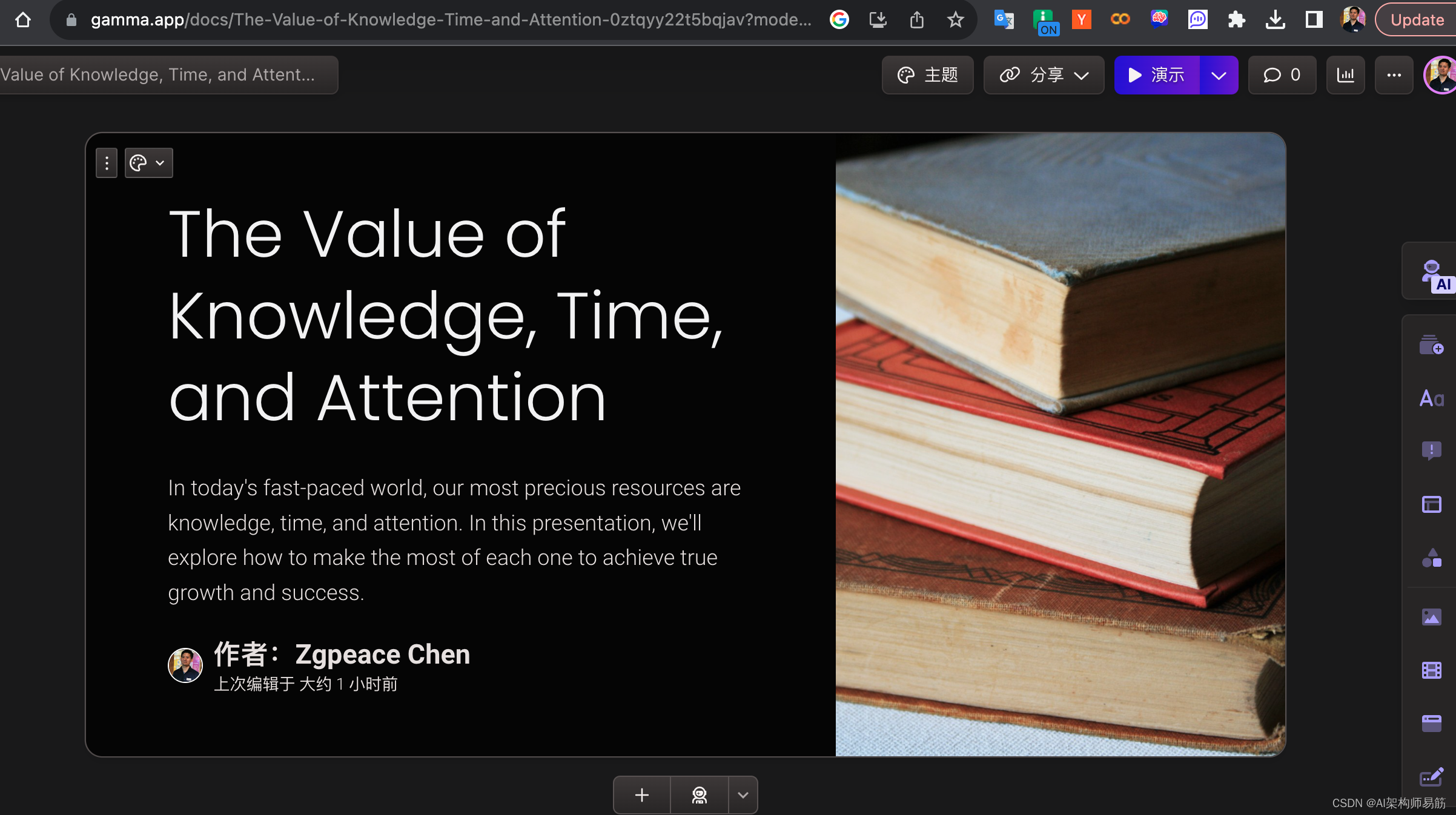
简单三步 用GPT-4和Gamma自动生成PPT PDF
1. 用GPT-4 生产PPT内容 我想把下面的文章做成PPT,请你给出详细的大纲和内容 用于谋生的知识,学生主要工作是学习,成年人的工作是养家糊口,这是基本的要求,在这之上,才能有更高的追求。 不要短期期望过高…...

QT设置弹窗显示屏幕中央
Qt设置每次运行弹窗显示屏幕中央 要确保Qt应用程序中的弹出窗口每次都显示在屏幕的中央,您可以使用以下方法: 使用QMessageBox的move方法手动设置窗口位置: #include <QApplication> #include <QMessageBox> #include <QDesk…...
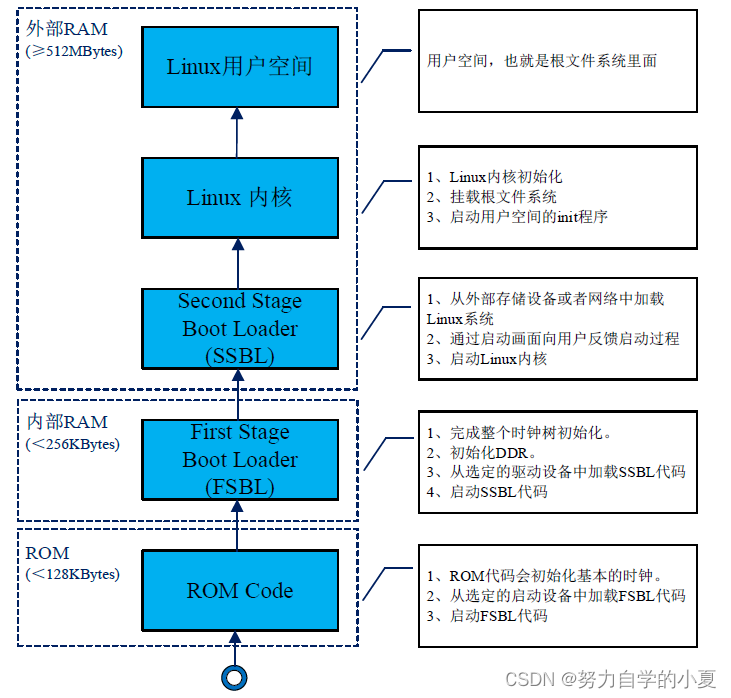
正点原子嵌入式linux驱动开发——STM32MP1启动详解
STM32单片机是直接将程序下载到内部 Flash中,上电以后直接运行内部 Flash中的程序。 STM32MP157内部没有供用户使用的 Flash,系统都是存放在外部 Flash里面的,比如 EMMC、NAND等,因此 STM32MP157上电以后需要从外部 Flash加载程序…...
FPGA的数字钟带校时闹钟报时功能VHDL
名称:基于FPGA的数字钟具有校时闹钟报时功能 软件:Quartus 语言:VHDL 要求: 1、计时功能:这是数字钟设计的基本功能,每秒钟更新一次,并且能在显示屏上显示当前的时间。 2、闹钟功能:如果当前的时间与闹钟设置的时…...
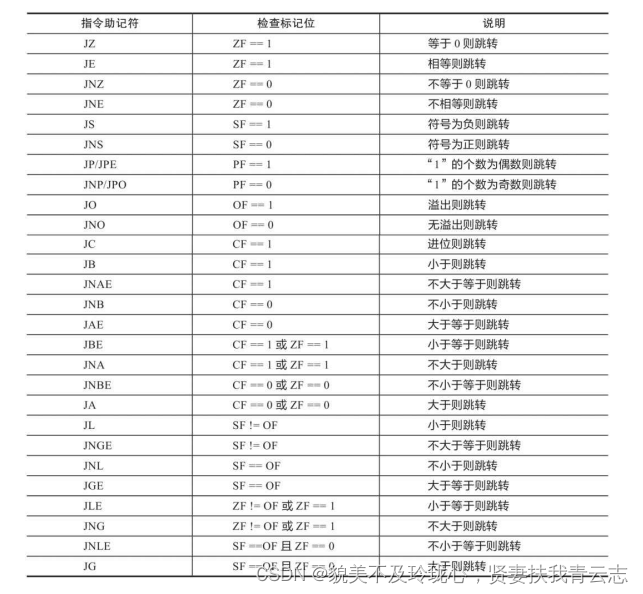
分析各种表达式求值过程
目录 算术运算与赋值 编译器常用的两种优化方案 常量传播 常量折叠 加法 Debug编译选项组下编译后的汇编代码分析 Release开启02执行效率优先 减法 Release版下优化和加法一致,不再赘述 乘法 除法 算术结果溢出 自增和自减 关系运算与逻辑运算 JCC指…...
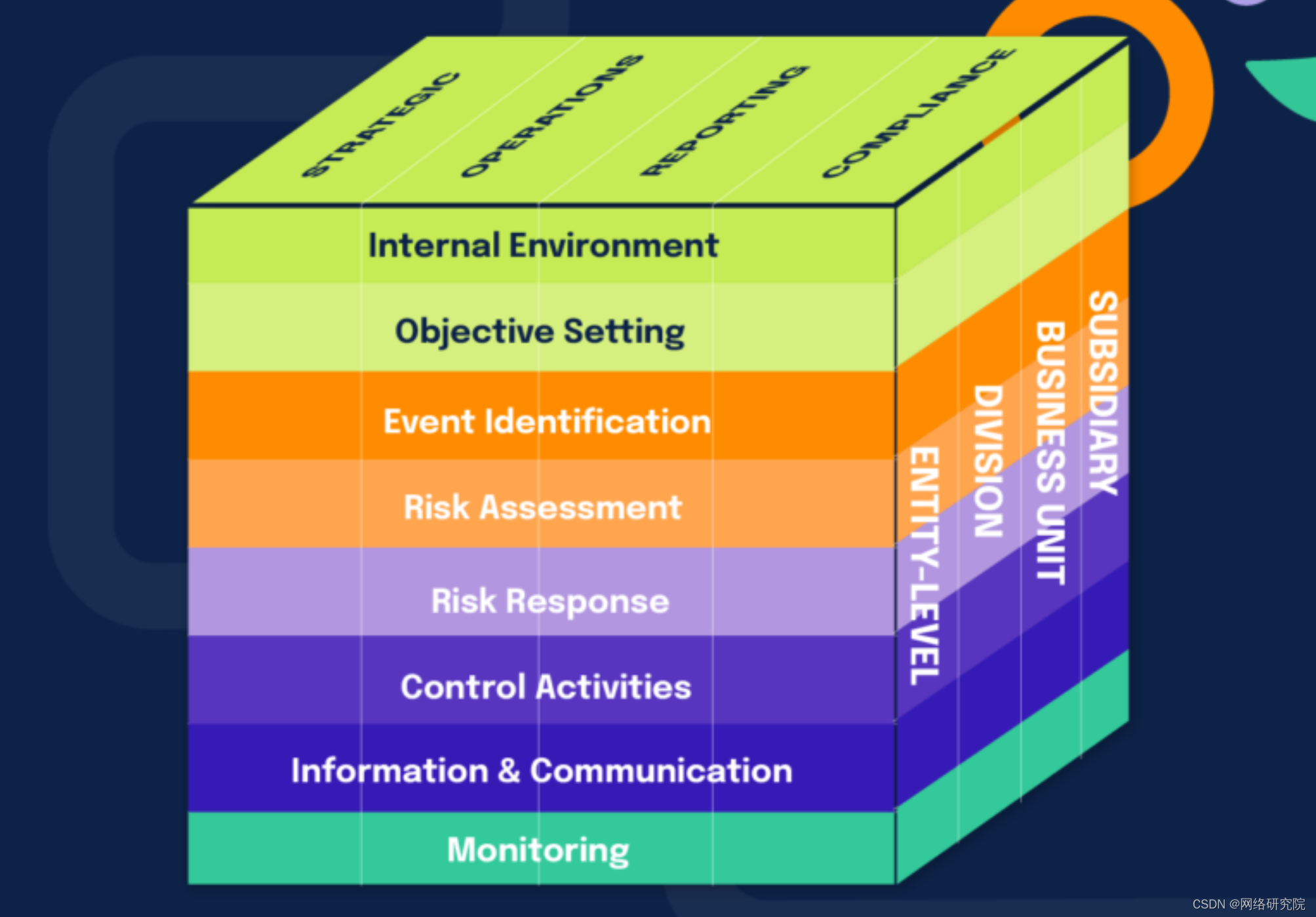
企业风险管理策略终极指南
企业风险管理不一定是可怕的。企业风险管理是一个模糊且难以定义的主题领域。它涵盖了企业的多种风险和程序,与传统的风险管理有很大不同。 那么,企业风险管理到底是什么?在本文中,我们将确定它是什么,提出两种常见的…...

OpenCV之分水岭算法(watershed)
Opencv 中 watershed函数原型: void watershed( InputArray image, InputOutputArray markers ); 第一个参数 image,必须是一个8bit 3通道彩色图像矩阵序列,第一个参数没什么要说的。关键是第二个参数 markers,Opencv官方文档的说…...

npm 命令
目录 初始化 搜索 安装 删除 更新 换源 查看 其他 补充 1.初始化 npm init #初始化一个package.json文件 npm init -y | npm init --yes 2.搜索 npm s jquery | npm search jquery 3.安装 npm install npm -g #更新到最新版本 npm i uniq | npm ins…...

【bug 记录】yolov5_C_demo 部署在 rv1126
问题1:opencv find 不到 在 CMakeLists 中将正确的 OpenCV库 路径添加到 CMAKE_PREFIX_PATH 变量中 set(CMAKE_PREFIX_PATH “/mnt/usr/local” ${CMAKE_PREFIX_PATH}) 问题2: rknn_api.h 找不到 将该文件从别处复制到项目 include 文件夹 问题3&…...
[vue-admin-template实战笔记]
1.克隆项目 git clone gitgitee.com:panjiachen/vue-admin-template.git 2.安装依赖 npm install 3.运行项目就会自动打开网页,并且热部署插件 npm run dev 4.查看代码 //将vue-admin-template拖入到idea中即可查看代码 1)并且发现,常用的东西已经集…...
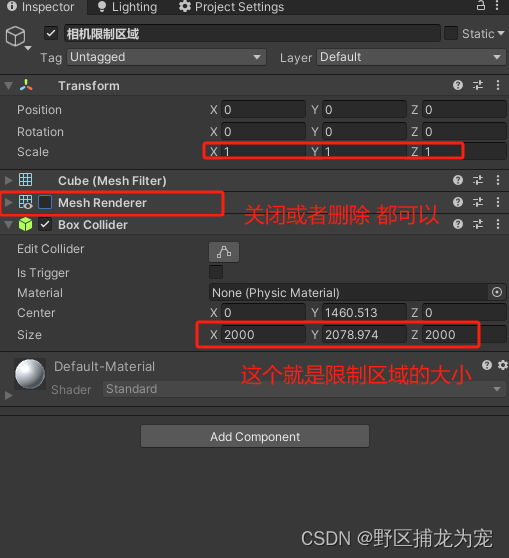
unity 限制 相机移动 区域(无需碰撞检测)
限制功能原著地址:unity限制相机可移动区域(box collider)_unity限制相机移动区域_manson-liao的博客-CSDN博客 一、创建限制区域 创建一个Cube,Scale大小1,添加组件:BoxCollder,调整BoxColld…...

Hudi第二章:集成Spark
系列文章目录 Hudi第一章:编译安装 Hudi第二章:集成Spark 文章目录 系列文章目录前言一、安装Spark1、安装Spark2.安装hive 二、spark-shell1.启动命令2.插入数据3.查询数据1.转换DF2.查询 3.更新4.时间旅行5.增量查询6.指定时间点查询7.删除数据1.获取…...

springboot和vue:八、vue快速入门
vue快速入门 新建一个html文件 导入 vue.js 的 script 脚本文件 <script src"https://unpkg.com/vuenext"></script>在页面中声明一个将要被 vue 所控制的 DOM 区域,既MVVM中的View <div id"app">{{ message }} </div…...

docker-compose内网本地安装
1:通过包管理器安装 Docker Compose,请按照以下步骤进行操作: 首先,确保你的系统上已经安装了 Docker。如果尚未安装 Docker,请根据你的操作系统使用适当的包管理器进行安装打开终端,并运行以下命令下载 D…...

ThreeJs的场景实现鼠标拖动旋转控制
前面一个章节中已经实现在场景中放置一个正方体,并添加灯光使得正方体可见。但是由于是静态的还不能证明是3D的,我们需要添加一些控制器,使得通过鼠标控制正方体可以动起来,实现真正的3D效果,由此引入OrbitControls组件…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...
