数据结构与算法-(7)---栈的应用-(3)表达式转换
🌈write in front🌈
🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流.
🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如需转载还请通知⚠️
📝个人主页:Aileen_0v0🧸—CSDN博客
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏:Aileen_0v0🧸的数据结构与算法学习系列专栏🌸——CSDN博客
🗼我的格言:"没有罗马,那就自己创造罗马💫~"

目录
编辑
编辑
回顾 🧸
编辑
中缀表达式🀄
全括号表达式与前后缀表达式的关系🎡
中缀表达式转换为前后缀形式的方法🪐
通用的中缀转后缀算法⭐
利用中缀转后缀的操作流程🪂
转成后缀表达式对应的代码🚀

回顾 🧸
"温故而知新"
通过思维导图回顾一下我们学了什么,我们先学了什么是线性结构,栈(Stack)是一种抽象数据类型的线性结构,栈是什么,栈的特点以及操作步骤,我们还可以通过列表去实现栈,不过不同的栈顶其对应的时间复杂度也不同,了解完栈的基础知识点后我们开始学习栈的应用,栈可以用于
「(1)匹配符号(Balance Symbols),
(2)进制转换(Decimal conversion),
(3)表达式转换(Experssion conversion)」
(1) 和 (2) 我们已经在前面的文章写过了:不记得知识点或者对前面内容感兴趣的小伙伴可以点击👉
🔗(1)http://t.csdnimg.cn/Ypv3q
🔗(2)http://t.csdnimg.cn/OLIJW
对应专栏数据结构与算法学习系列专栏🌸🔗:http://t.csdnimg.cn/6BQDo
中缀表达式🀄
我们通常看到的表达式如:B*C , 很容易就知道是B乘以C
像 * 这种操作符( operator ) 介于操作数 ( operand )中间的表示法,称为 "中缀" 表示法.
But sometimes 中缀表示法会 case confusion(引起混淆),如 "A + B * C"
是A+B然后再乘以C 还是B*C然后再加A?
为了消除混淆,人们引入"优先级"的概念
规定高优先级的操作符先计算
相同优先级的操作符从左到右依次计算这样A+B*C就没有疑义是A加上 B与C的乘积
同时引入了括号来表示强制优先级,括号的优先级最高,而且在嵌套的括号中,内层的优先级更高这样(A+B)*C就是A与B的和再乘以C
全括号表达式与前后缀表达式的关系🎡
虽然人们已经习惯了这种表示法,但计算机处理最好是能明确规定所有的计算顺序,这样无需处理复杂的优先规则
于是,我们引入全括号表达式:
在所有的表达式项两边都加上括号A+B*C+D,应表示为((A+(B*C))+D)
可否将表达式中操作符的位置稍移动一下?
例如中缀表达式A+B将操作符移到前面,变为"+AB"
或者将操作符移到最后,变为“AB+”
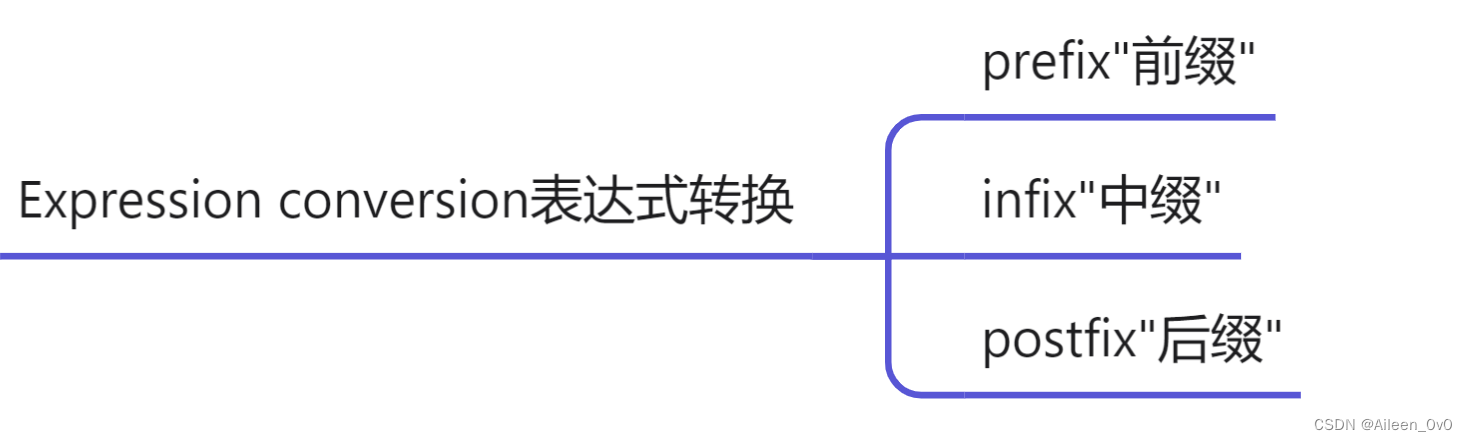
我们就得到了表达式的另外两种表示法:"前缀"和“后缀”表示法以操作符相对于操作数的位置来定义
这样A+B*C将变为前缀的"+A*BC"后缀的"ABC*+"为了帮助理解,子表达式加了下划线
在前缀和后缀表达式中,操作符的次序完全决定了运算的次序,不再有混淆
所以在很多情况下,表达式在计算机中的表示都避免使用复杂的中缀形式
让我们先看看这些前中缀和后缀表达式
| 中缀表达式 | 前缀表达式 | 后缀表达式 |
| A + B * C + D | + + A * B C D | A B C * + D + |
| ( A + B ) * ( C + D ) | * + A B + C D | A B + C D + * |
| A * B + C * D | + * A B * C D | A B * C D * + |
| A + B + C + D | + + + A B C D | A B + C + D + |
想必初看的小伙伴会觉得眼花缭乱,但是不要着急,我们接下来会一一讲解.
一定得有个算法来转换任意复杂的表达式
为了分解算法的复杂度,我们从“全括号中缀表达式入手我们看A+B*C,
如果写成全括号形式:(A+(B*C)),显式表达了计算次序我们注意到每一对括号,都包舍了一组完整的操作符和操作数,让我们看看如何将其转换成前后缀表达式吧~

中缀表达式转换为前后缀形式的方法🪐
✨Summary:
(1)将中缀表达式转换为全括号形式
(2)将所有的操作符移动到子表达式所在的 左括号(前缀prefix) 或者 右括号(后缀postfix) 处~
替代之,再删除所有的括号.
通用的中缀转后缀算法⭐
在中缀表达式转换为后缀形式的处理过程中,操作符比操作数要晚输出
所以在扫描到对应的第二个操作数之前,需要把操作符先保存起来
而这些暂存的操作符,由于优先级的规则还有可能要反转次序输出.
在A+B*C中,+虽然先出现,但优先级比后面这个*要低,所以它要等*处理完后,才能再处理.
这种反转特性,使得我们考虑用栈来保存暂时未处理的操作符
再看看(A+B)*C,对应的后缀形式是AB+C*
这里+的输出比*要早,主要是因为括号使得+的优先级提升,高于括号之外的*
根据上面的“全括号”表达式,后缀表达式中操作符应该出现在左括号对应的右括号位置
所以遇到左括号,要标记下,其后出现的操作符优先级提升了,一旦扫描到对应的右括号,就可以马上输出这个操作符
总结:
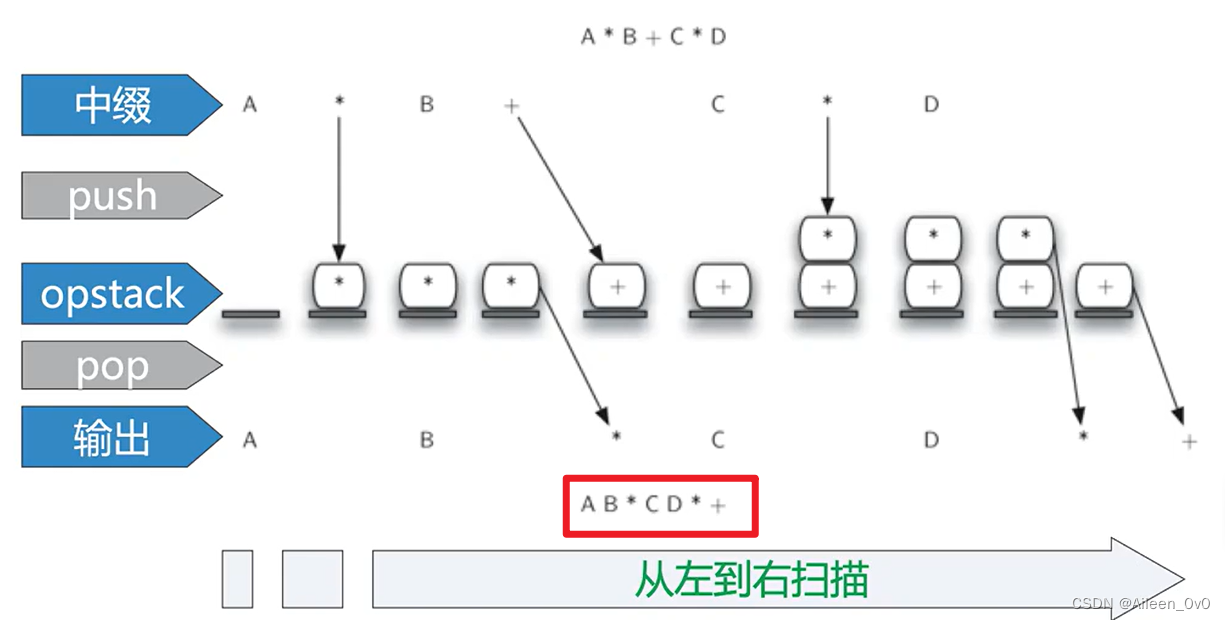
在从左到右扫描逐个字符扫描中缀表达式的过程中,采用一个栈来暂存未处理的操作符
这样,栈顶的操作符就是最近暂存进去的,当遇到一个新的操作符,就需要跟栈顶的操作符比较下优先级,再行处理--->新符号和栈顶对比,新的高,就入栈(因为取时也先取); 新的低,就把栈顶出栈,让栈顶的先运算.
利用中缀转后缀的操作流程🪂
后面的算法描述中,约定中缀表达式是由空格隔开的一系列单词(token)构成,
操作符单词包括*/+-()
而操作数单词则是单字母标识符A、B、C等。
1.首先,创建空栈opstack用于暂存操作符,空表postfixList用于保存后缀表达式
2.将中缀表达式转换为单词(token)列表
A + B*C = split => ['A', '+', 'B', ' * ', 'C']


图解:
转成后缀表达式对应的代码🚀
class Stack:#Stack---->ADTdef __init__(self):self.items =[]def isEmpty(self):return self.items == []# 满足这些属性(行为)的是栈def push(self,item):self.items.append(item)def pop(self):return self.items.pop()def peek(self):return self.items[len(self.items)-1]#def size(self):return len(self.items)def infixToPostfix(infixexpr):# 记录操作符优先级prec = {}prec["*"] = 3prec["/"] = 3prec["+"] = 2prec["-"] = 2prec["("] = 1opStack = Stack()postfixList = []# 解析表达式到列表tokenList = infixexpr.split()for token in tokenList:# 操作数if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":postfixList.append(token)# (elif token == "(":opStack.push(token)# )elif token == ")":topToken = opStack.pop()while topToken != '(':postfixList.append(topToken)topToken = opStack.pop()# 操作符else:while (not opStack.isEmpty()) and \(prec[opStack.peek()] >= prec[token]):postfixList.append(opStack.pop())opStack.push(token)while not opStack.isEmpty():# 操作符postfixList.append(opStack.pop())# 合成后缀表达式字符串 return " ".join(postfixList)
print(infixToPostfix("A + B * C "))运行代码测试结果 :


相关文章:

数据结构与算法-(7)---栈的应用-(3)表达式转换
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...
)
Lilliefors正态性检验(一种非参数统计方法)
Lilliefors检验(也称为Kolmogorov-Smirnov-Lilliefors检验)是一种用于检验数据是否符合正态分布的统计检验方法,它是Kolmogorov-Smirnov检验的一种变体,专门用于小样本情况。与K-S检验不同,Lilliefors检验不需要假定数…...
)
【云原生】配置Kubernetes CronJob自动备份MySQL数据库(单机版)
文章目录 每天自动备份数据库MySQL【云原生】配置Kubernetes CronJob自动备份Clickhouse数据库 每天自动备份数据库 MySQL 引用镜像:databack/mysql-backup,使用文档:https://hub.docker.com/r/databack/mysql-backup 测试、开发环境:每天0点40分执行全库备份操作,备份文…...
基于PSO算法的功率角摆动曲线优化研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
)
数论知识点总结(一)
文章目录 目录 文章目录 前言 一、数论有哪些 二、题法混讲 1.素数判断,质数,筛法 2.最大公约数和最小公倍数 3.快速幂 4.约数 前言 现在针对CSP-J/S组的第一题主要都是数论,换句话说,持数论之剑,可行天下矣! 一、数论有哪些 数论 原根,素数判断,质数,筛法最大公约数…...

知识分享 钡铼网关功能介绍:使用SSLTLS 加密,保证MQTT通信安全
背景 为了使不同的设备或系统能够相互通信,让旧有系统和新的系统可以集成,通信更加灵活和可靠。以及将数据从不同的来源收集并传输到不同的目的地,实现数据的集中管理和分发。 通信网关完美克服了这一难题,485或者网口的设备能通过…...

asp.net core mvc区域路由
ASP.NET Core 区域路由(Area Routing)是一种将应用程序中的路由划分为多个区域的方式,类似于 MVC 的控制器和视图的区域划分。区域路由可以帮助开发人员更好地组织应用程序的代码和路由,并使其更易于维护。 要使用区域路由&#…...
KNN(下):数据分析 | 数据挖掘 | 十大算法之一
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...

Servlet开发-session和cookie理解案例-登录页面
项目展示 进入登录页面,输入正确的用户名和密码以后会自动跳到主页 登录成功以后打印用户名以及上次登录的时间,如果浏览器和客户端都保存有上次登录的信息,则不需要登录就可以进入主页 编码思路 1.首先提供一个登录的前端页面&…...
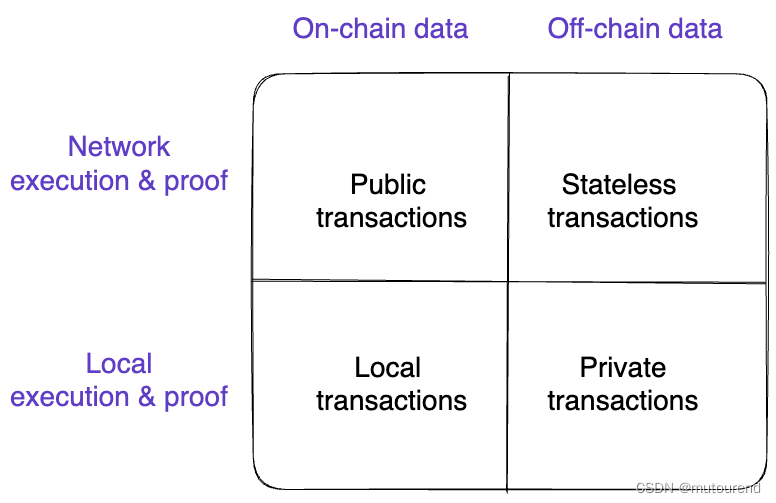
Polygon Miden:扩展以太坊功能集的ZK-optimized rollup
1. 引言 Polygon Miden定位为zkVM,定于2023年Q4上公开测试网。 zk、zkVM、zkEVM及其未来中指出,当前主要有3种类型的zkVM,括号内为其相应的指令集: mainstream(WASM, RISC-V)EVM(EVM bytecod…...

[题]宝物筛选 #单调队列优化
五、宝物筛选(洛谷P1776) 题目链接 好家伙,找到了一个之前学习多重背包优化时的错误…… 之前记的笔记还是很有用的…… #include<bits/stdc.h> using namespace std; const int N 1e5 10; int f[N]; int n, m; int v, w, s; int l…...

.NET的键盘Hook管理类,用于禁用键盘输入和切换
一、MyHook帮助类 此类需要编写指定屏蔽的按键,灵活性差。 using System; using System.Runtime.InteropServices; using System.Diagnostics; using System.Windows.Forms; using Microsoft.Win32;namespace MyHookClass {/// <summary>/// 类一/// </su…...

Anaconda Jupyter
🙌秋名山码民的主页 😂oi退役选手,Java、大数据、单片机、IoT均有所涉猎,热爱技术,技术无罪 🎉欢迎关注🔎点赞👍收藏⭐️留言📝 获取源码,添加WX 目录 前言An…...
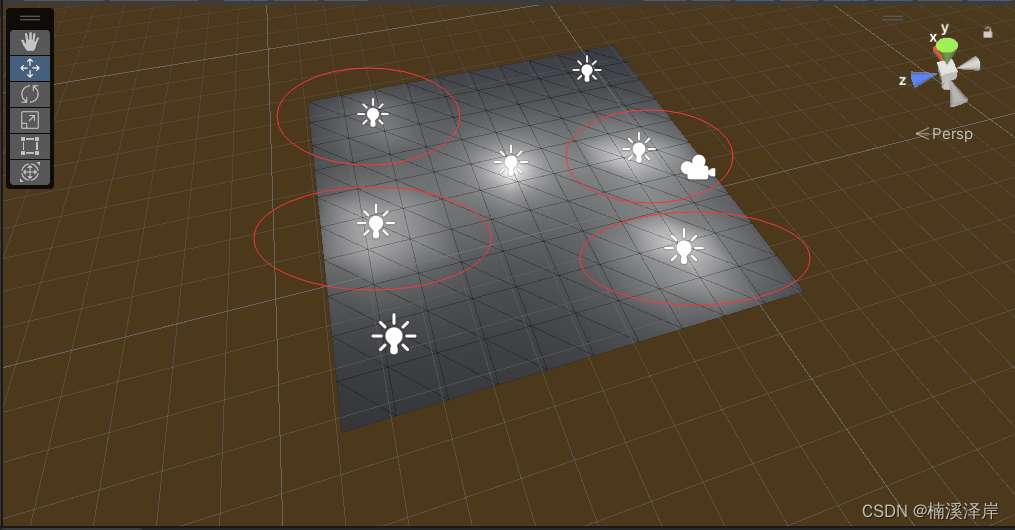
Unity中Shader的前向渲染路径ForwardRenderingPath
文章目录 前言一、前向渲染路径的特点二、渲染方式1、逐像素(效果最好)2、逐顶点(效果次之)3、SH球谐(效果最差) 三、Unity中对灯光设置 后,自动选择对应的渲染方式1、ForwardBase仅用于一个逐像素的平行灯,以及所有的逐顶点与SH2、ForwardAdd用于其他所…...

简历项目优化关键方法论-START
START方法论是非常著名的面试法则,经常被面试官使用的工具 Situation:情况、事情、项目需求是在什么情况下发生Task:任务,你负责的做的是什么Action:动作,针对这样的情况分析,你采用了什么行动方式Result:结果,在这样…...
TensorFlow学习1:使用官方模型进行图片分类
前言 人工智能以后会越来越发达,趁着现在简单学习一下。机器学习框架有很多,这里觉得学习谷歌的 TensorFlow,谷歌的技术还是很有保证的,另外TensorFlow 的中文文档真的很友好。 文档: https://tensorflow.google.cn/…...
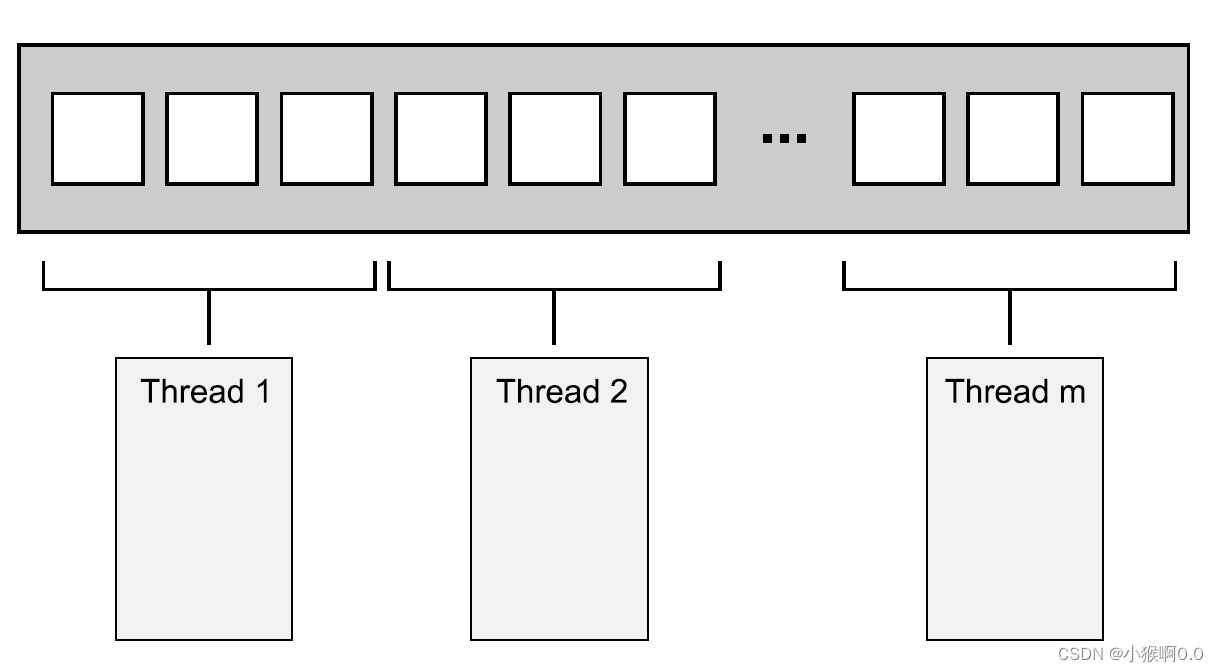
C++ 并发编程实战 第八章 设计并发代码 一
目录 8.1 在线程间切分任务 8.1.1 先在线程间切分数据,再开始处理 8.1.2 以递归方式划分数据 8.1.3 依据工作类别划分任务 借多线程分离关注点需防范两大风险 在线程间按流程划分任务 8.2 影响并发性能的因素 8.2.1 处理器的数量 8.2.2 数据竞争和缓存兵乓…...
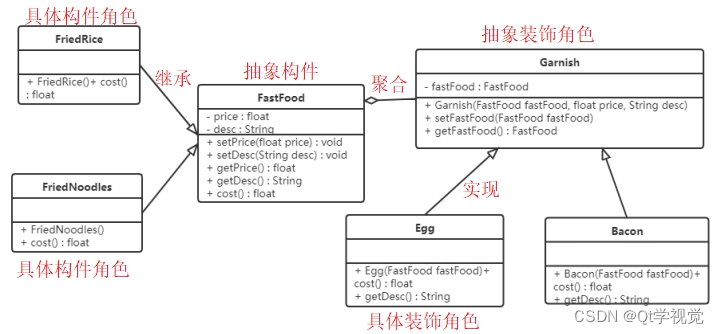
设计模式8、装饰者模式 Decorator
解释说明:动态地给一个对象增加一些额外的职责。就扩展功能而言,装饰模式提供了一种比使用子类更加灵活的替代方案 抽象构件(Component):定义一个抽象接口以规范准备收附加责任的对象 具体构件(ConcreteCom…...
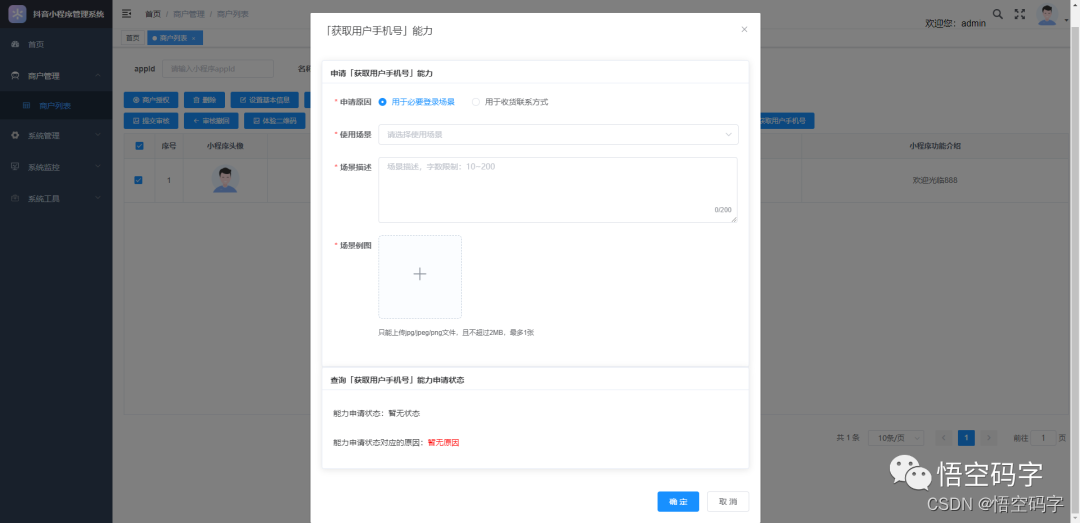
抖音开放平台第三方代小程序开发,一整套流程
大家好,我是小悟 抖音小程序第三方平台开发着力于解决抖音生态体系内的小程序管理问题,一套模板,随处部署。能尽可能地减少服务商的开发成本,服务商只用开发一套小程序代码作为模板就可以快速批量的孵化出大量的商家小程序。 第…...

Flutter笔记:滚动之-无限滚动与动态加载的实现(GetX简单状态管理版)
Flutter笔记 无限滚动与动态加载的实现(GeX简单状态管理版) 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...