【CSAPP】整数运算
文章目录
- 无符号加法
- 练习1
- 练习2
- 补码加法
- 练习1
- 练习2
- 练习3
- 练习4
- 补码的非
- 练习
- 无符号乘法
- 补码乘法
- 练习1
- 练习2
- 练习3
- 乘以常数
- 练习1
- 练习2
- 除以2的幂
- 练习1
- 练习2
- 关于整数运算的最后思考
- 练习
无符号加法
考虑两个非负整数x和y,满足0≤x,y<2w0 \le x, y < 2^w0≤x,y<2w,每个数都能表示为一个w位的无符号数。如果要计算x+y,其结果的可能取值范围是0≤x+y≤2w+1−20 \le x+y \le 2^{w+1}-20≤x+y≤2w+1−2,表示该值可能需要w+1位。如果x+y的结果又要和别的数做加法,那可能需要更多的位表示运算结果。这种字长膨胀意味着,要想完整地表示运算的结果,我们不能对整型长度做任何限制。
但实际情况是,在C语言中,整型变量占固定大小的字节和位,当整数运算结果超出了整型变量的表示范围时,计算机运算的结果是截断后的值,与预期值有偏差。
我们定义操作+wu+^u_w+wu是w位的无符号加法。
原理:无符号数加法。
对满足0≤x,y<2w0 \le x,y<2^w0≤x,y<2w的xxx和yyy,有:
x+wuy={x+y,0≤x+y≤2w−1x+y−2w,2w≤x+y≤2w+1−2\begin{align} x+^u_wy= \begin{cases} x+y,\quad &0 \le x+y \le 2^w -1 \\ x + y-2^w, \quad &2^w \le x+y \le 2^{w+1}-2 \end{cases} \end{align} x+wuy={x+y,x+y−2w,0≤x+y≤2w−12w≤x+y≤2w+1−2
说一个算术运算溢出,是指完整的整数结果不能被有限的整型长度所表示,产生了高有效位的丢失。
执行C程序时,系统不会因运算发生溢出而自己报错,因此程序员必须关注该情况。
原理:检测无符号加法中的溢出。
对满足0≤x,y≤2w−10 \le x,y \le 2^w-10≤x,y≤2w−1的x和y,存在s=˙x+wuys\.=x+^u_wys=˙x+wuy,当且仅当s<xs < xs<x,s<ys<ys<y时,运算发生了溢出。
- 证明:当s<xs < xs<x,s<ys<ys<y时,运算发生了溢出。
因为x≥0x\ge 0x≥0,因此x+y≥yx+y \ge yx+y≥y,因此s≥ys \ge ys≥y,所以当s<ys<ys<y时,发生运算错误(即溢出)。
因为y≥0y \ge0y≥0,因此x+y≥xx+y \ge xx+y≥x,因此s≥xs \ge xs≥x,所以当s<xs<xs<x时,发生运算错误(即溢出)。 - 证明:当运算发生溢出时,s<xs < xs<x,s<ys<ys<y。
运算发生溢出时,s=x+y−2ws=x+y-2^ws=x+y−2w,因为y<2wy<2^wy<2w,因此y−2w<0y-2^w<0y−2w<0,因此s<xs<xs<x。
运算发生溢出时,s=y+x−2ws=y+x-2^ws=y+x−2w,因为x<2wx<2^wx<2w,因此x−2w<0x-2^w<0x−2w<0,因此s<ys<ys<y。
对任何一个数xxx而言,存在−x-x−x使得−x+x=0-x+x=0−x+x=0,则称−x-x−x是xxx的加法逆元,xxx也是−x-x−x的加法逆元。加法逆元即取反。
原理:无符号数取反。
对满足0≤x≤2w−10 \le x \le 2^w-10≤x≤2w−1的x,其w位的无符号加法逆元−wu-^u_w−wu可表示为:
−wux={x,x=02w−x,x>0\begin{align} -^u_wx= \begin{cases} x,\quad &x=0\\ 2^w-x,\quad &x>0 \end{cases} \end{align} −wux={x,2w−x,x=0x>0
练习1
实现一个函数,如果参数x和y相加不会产生溢出,这个函数就返回1。
int uadd_ok(unsigned x, unsigned y)
{unsigned s = x + y;return s >= x;
}
练习2
给出下表中数的无符号加法逆元 −4u-^u_4−4u 的位表示。
| x | -x | ||
| 十六进制 | 十进制 | 十六进制 | 十进制 |
| 0x0 | 0 | 0x0 | 0 |
| 0x5 | 5 | 0xB | 11 |
| 0x8 | 8 | 0x8 | 8 |
| 0xD | 13 | 0x3 | 3 |
| 0xF | 15 | 0x1 | 1 |
补码加法
对满足−2w−1≤x,y≤2w−1−1-2^{w-1} \le x,y \le 2^{w-1}-1−2w−1≤x,y≤2w−1−1的x和y,x + y的取值范围是−2w≤x+y≤2w−2-2^w \le x+y \le 2^w-2−2w≤x+y≤2w−2。跟无符号加法一样,当运算结果不能用w位表示时,会截断数据,产生运算溢出。
我们使用操作+wt+^t_w+wt表示w位的补码加法。
原理:补码加法。
对满足−2w−1≤x,y≤2w−1−1-2^{w-1} \le x,y \le 2^{w-1}-1−2w−1≤x,y≤2w−1−1的xxx和yyy,有:
x+wty={x+y+2w,x+y<−2w−1负溢出x+y,−2w−1≤x+y≤2w−1−1正常x+y−2w,x+y≥2w−1正溢出\begin{align} x+^t_wy= \begin{cases} x+y+2^w, \quad &x+y < -2^{w-1} \quad &负溢出\\ x+y, \quad &-2^{w-1} \le x+y \le 2^{w-1}-1 \quad &正常 \\ x+y-2^w,\quad &x+y \ge 2^{w-1} &正溢出 \end{cases} \end{align} x+wty=⎩⎨⎧x+y+2w,x+y,x+y−2w,x+y<−2w−1−2w−1≤x+y≤2w−1−1x+y≥2w−1负溢出正常正溢出
在
bit层面,无符号加法和补码加法的运算规则是一样的,都是逢二进一。
负溢出指运算结果太小了,小于−2w−1-2^{w-1}−2w−1;正溢出指运算结果太大了,大于2w−1−12^{w-1}-12w−1−1。溢出产生了符号翻转。
原理:检测补码加法中的溢出。
对满足−2w−1≤x,y≤2w−1−1-2^{w-1} \le x,y \le 2^{w-1}-1−2w−1≤x,y≤2w−1−1的x和y,存在s=˙x+ys\.=x+ys=˙x+y。当且仅当x>0x>0x>0,y>0y>0y>0,s≤0s\le0s≤0时,算术运算正溢出;当且仅当x<0x<0x<0,y<0y<0y<0,s≥0s\ge0s≥0时,算术运算负溢出。
- 证明:x>0x>0x>0,y>0y>0y>0,s≤0s\le0s≤0时,算术运算正溢出。
预期s=x+y>0s=x+y>0s=x+y>0而s≤0s\le0s≤0,显然s过大而无法表示,运算产生了错误(正溢出)。 - 证明:算术运算正溢出,因此x>0x>0x>0,y>0y>0y>0时s≤0s\le0s≤0。
运算正溢出,那么s=x+y−2ws=x+y-2^ws=x+y−2w,且2w−1≤x+y≤2w−22^{w-1}\le x+y \le 2^{w}-22w−1≤x+y≤2w−2,因此x>0x>0x>0,y>0y>0y>0,且2w−1−2w≤s≤2w−2−2w2^{w-1}-2^w \le s \le 2^{w}-2-2^w2w−1−2w≤s≤2w−2−2w,即−2w−1≤s≤−2≤0-2^{w-1} \le s \le -2 \le 0−2w−1≤s≤−2≤0,即s≤0s\le0s≤0。 - 证明:x<0x<0x<0,y<0y<0y<0,s≥0s\ge0s≥0时,算术运算负溢出。
预期s=x+y<0s=x+y<0s=x+y<0而s≥0s\ge0s≥0,显然s过小而无法表示,运算产生了错误(负溢出)。 - 算术运算负溢出,因此x<0x<0x<0,y<0y<0y<0时s≥0s\ge0s≥0。
运算负溢出,那么s=x+y+2ws=x+y+2^ws=x+y+2w,且−2w≤x+y<−2w−1-2^{w}\le x+y < -2^{w-1}−2w≤x+y<−2w−1,因此x<0x<0x<0,y<0y<0y<0,且−2w+2w≤s≤−2w−1+2w-2^{w}+2^w \le s \le -2^{w-1}+2^w−2w+2w≤s≤−2w−1+2w,即0≤s≤2w−10 \le s \le 2^{w-1}0≤s≤2w−1,即s≥0s\ge0s≥0。
练习1
填写下表
| xxx | yyy | x+yx+yx+y | x+5tx+^t_5x+5t | 情况 |
|---|---|---|---|---|
[10100]-12 | [10001]-15 | [100101]-27 | [00101]5 | 负溢出 |
[11000]-8 | [11000]-8 | [110000]-16 | [10000]-16 | 正常 |
[10111]-9 | [01000]8 | [11111]-1 | [11111]-1 | 正常 |
[00010]2 | [00101]5 | [00111]7 | [00111]7 | 正常 |
[01100]12 | [00100]4 | [10000]16 | [10000]-16 | 正溢出 |
练习2
实现一个函数tadd_ok,参数x和y补码相加不产生溢出时,返回1。
int tadd_ok(int x, int y)
{int s = x + y;return !((x > 0 && y > 0 && s <= 0) || (x < 0 && y < 0 && s >= 0));
}
练习3
如下实现存在什么问题?
int tadd_ok(int x, int y)
{int sum = x + y;return (sum - x == y) && (sum - y == x);
}
函数会永远返回1。因为并没有检测到越界的进位。
练习4
下面的函数在计算x - y不溢出时,返回1。
int tsub_ok(int x, int y)
{return tadd_ok(x, -y);
}
x和y取什么值时,该函数会产生错误的结果?写一个该函数的正确版本。
当y的取值为INT_MIN时,-y的取值也为INT_MIN。因此在计算机看来,x-y就是x+y。
此时按现实的整数运算来看,如果x >= 0,x-y预期运算溢出,返回0;如果如果x < 0,x-y预期运算不溢出,返回1。
但在计算机看来,如果x >= 0,tadd_ok(x, -y)不溢出,返回1;如果x < 0,tadd_ok(x, -y)溢出,返回0。
我们以为它做的是减法,实际上它做的是加法。
在计算机运算中,
INT_MIN的位级表示是[1, 0, …, 0],-INT_MIN的位级表示也是[1, 0, …, 0],因为[1, 0, …, 0] + [1, 0, …, 0] = [0, 0, …, 0]。当然,这不符合现实的整数运算规则。
正确的写法如下:
int tsub_ok(int x, int y)
{if (y == INT_MIN) {return !tadd_ok(x, -y);}return tadd_ok(x, -y);
}
补码的非
取非就是求加法逆元。
对满足TMinw≤x≤TMaxwTMin_w \le x \le TMax_wTMinw≤x≤TMaxw的x,其补码的非−wtx-^t_wx−wtx表示为:
−wtx={TMinw,x=TMinw−x,TMinw<x≤TMaxw\begin{align} -^t_wx= \begin{cases} TMin_w, \quad &x=TMin_w \\ -x, \quad &TMin_w < x \le TMax_w \end{cases} \end{align} −wtx={TMinw,−x,x=TMinwTMinw<x≤TMaxw
在
C语言中,可以说,对于任意整数值x,因为x + ~x + 1 = 0,所以-x = ~x + 1。
练习
填写下表。
| xxx | −4tx-^t_4x−4tx |
|---|---|
0x00 | 0x00 |
0x55 | 0xB-5 |
0x8-8 | 0x8-8 |
0xD-3 | 0x33 |
0xF-1 | 0x11 |
无符号乘法
两个w位的无符号数相乘,其结果可能需要2w个位才能完整表示。但在C语言中,会根据整数位宽做截断处理。
对满足0≤x,y≤2w−10 \le x,y \le 2^w-10≤x,y≤2w−1的x和y,有:
x∗wuy=˙(x∗y)mod2w\begin{align} x *^u_w y\.=(x * y) mod 2^w \end{align} x∗wuy=˙(x∗y)mod2w
补码乘法
对满足−2w−1≤x,y≤2w−1−1-2^{w-1} \le x,y \le 2^{w-1}-1−2w−1≤x,y≤2w−1−1的x和y,有:
x∗wty=˙U2Tw((x∗y)mod2w)\begin{align} x *^t_w y\.=U2T_w((x * y) mod 2^w) \end{align} x∗wty=˙U2Tw((x∗y)mod2w)
w位无符号乘法和w位补码乘法的运算结果的低w位是一样的,区别在于解释这些位的方式。
练习1
填写下表,位宽w=3。
| 模式 | xxx | yyy | x∗yx*yx∗y | 截断的x*y |
|---|---|---|---|---|
| 无符号 | [100]4 | [101]5 | [010100]20 | [100]4 |
| 补码 | [100]-4 | [101]-3 | [001100]12 | [100]-4 |
| 无符号 | [010]2 | [111]7 | [001110]14 | [110]6 |
| 补码 | [010]2 | [111]-1 | [111110]-2 | [110]-2 |
| 无符号 | [110]6 | [110]6 | [100100]36 | [100]4 |
| 补码 | [110]-2 | [110]-2 | [000100]4 | [100]4 |
计算二进制
w位的无符号乘法时,先做零扩展,扩展到2w位,再两数相乘,取低2w位。
计算二进制w位的补码乘法时,先做符号扩展,扩展到2w位,再两数相乘,取低2w位。
练习2
考虑下面的函数,它判断两个参数是否会产生溢出,不溢出返回1。
int tmul_ok(int x, int y)
{int p = x * y;return !x || p/x == y;
}
当x = 0时,乘法不溢出,函数返回1。和预期相符。
当x不等于0时:
- x∗y=p+t2wx*y=p+t2^wx∗y=p+t2w,其中t≠0t\ne 0t=0当且仅当计算溢出。
当t≠0t\ne 0t=0时,x∗y>px*y>px∗y>p或者x∗y<px*y<px∗y<p,计算溢出。
如果计算溢出,p<x∗yp<x*yp<x∗y或者p>x∗yp>x*yp>x∗y,所以t≠0t\ne 0t=0。 - p=x∗q+rp=x*q+rp=x∗q+r,其中
q是p/xp/xp/x的结果,|r| < |x|。
r是p除以x的余数,因此一定存在|r| < |x|。 q = y当且仅当r = t = 0。
q = y时,x∗q=p+t2wx*q=p+t2^wx∗q=p+t2w,因此x∗q+r=p+t2w+rx*q+r=p+t2^w+rx∗q+r=p+t2w+r,因此p=p+t2w+rp=p+t2^w+rp=p+t2w+r,因此0=0+t2w+r0=0+t2^w+r0=0+t2w+r,所以r = t = 0。
r = t = 0时,x∗y=x∗q+t2wx*y=x*q+t2^wx∗y=x∗q+t2w,因此y=q+t2wxy=q+\frac {t2^w}{x}y=q+xt2w,因此q = y。
计算溢出时,r≠0r \ne 0r=0,t≠0t \ne 0t=0,因此q≠yq\ne yq=y,p/x≠yp/x \ne yp/x=y,函数返回0。反之不溢出,函数返回1。
练习3
对于数据类型int为32位的情况,设计一个tmul_ok函数,使用64位精度的数据类型int64_t,不使用除法。不溢出返回1。
int tmul_ok(int x, int y)
{int64_t p = (int64_t)x * y;return p == (int)p; // 截断前后的值是不是一样
}
乘以常数
在大多数机器上,整数乘法指令相当慢。因此,编译器使用了一项重要的优化,就是用移位和加减法运算的组合来代替与常数因子的乘法。当然,如果数个移位和加减法指令比一个乘法指令更耗时,那就用乘法指令。
一个整数乘以2k2^k2k等价于左移k位(k≥0k \ge 0k≥0)。
练习1
LEA指令能够执行如(a << k) + b这样的运算。考虑b = 0或者b = a、k为任意可能的值,一条LEA指令可以计算a的哪些倍数?
当b = 0时,一条LEA指令可以计算a的20,21,22,23,...2^0,2^1,2^2,2^3,...20,21,22,23,...倍。
当b = a时,一条LEA指令可以计算a的20+1,21+1,22+1,23+1,...2^0 + 1,2^1 + 1,2^2 + 1,2^3 + 1,...20+1,21+1,22+1,23+1,...倍。
练习2
填写下表。
| kkk | 移位 | 加法/减法 | 表达式 |
|---|---|---|---|
| 6 | 2 | 1 | (x<<3)−(x<<1)(x<<3)-(x<<1)(x<<3)−(x<<1) |
| 31 | 1 | 1 | (x<<5)−x(x<<5)-x(x<<5)−x |
| -6 | 2 | 1 | (x<<1)−(x<<3)(x<<1)-(x<<3)(x<<1)−(x<<3) |
| 55 | 2 | 2 | (x<<6)−x−(x<<3)(x << 6) - x - (x << 3)(x<<6)−x−(x<<3) |
除以2的幂
在大多数机器上,整数除法比整数乘法还慢。
除以2的幂可以用右移实现,无符号数使用逻辑右移,有符号数使用算术右移。
对于任何实数α\alphaα,定义⌈α⌉\lceil \alpha \rceil⌈α⌉为唯一的整数α′\alpha'α′,使得α′−1<α≤α′\alpha'-1 < \alpha \le \alpha'α′−1<α≤α′。
对于任何实数α\alphaα,定义⌊α⌋\lfloor \alpha \rfloor⌊α⌋为唯一的整数α′\alpha'α′,使得α′≤α<α′+1\alpha' \le \alpha <\alpha'+1α′≤α<α′+1。
对于x≥0,y>0x\ge0,y>0x≥0,y>0,xxx除以yyy的结果是⌊x/y⌋\lfloor x/y \rfloor⌊x/y⌋;对于x<0,y>0x<0,y>0x<0,y>0或x>0,y<0x>0,y<0x>0,y<0,xxx除以yyy的结果是⌈x/y⌉\lceil x/y \rceil⌈x/y⌉。即向零取整。
计算机执行除法运算时,不论结果正负,都是向下取整。
如果要向上取整,需要给被除数加上偏置量(除数-1)。
⌈x/y⌉=⌊(x+y−1)/y⌋\begin{align} \lceil x/y \rceil=\lfloor (x+y-1)/y \rfloor \end{align} ⌈x/y⌉=⌊(x+y−1)/y⌋
C表达式(x < 0 ? x + (1 << k) - 1 : x) >> k将会计算x/2kx/2^kx/2k。
同乘法不同,我们不能用右移和加减运算的组合表示除以任意常数。(乘法满足分配律,但除法不)。
练习1
写一个函数div16,返回x/16的结果。
int div16(int x)
{int sign = x >> 31; // 符号位填满intint k = 4;int bias = (1 << k) - 1;return (x + sign & bias) >> k;
}
练习2
下面的代码中,省略了M和N的定义。
int arith(int x, int y)
{return x * M + y / N;
}
编译器优化后:
int arith(int x, int y)
{int t = x;x <<= 5;x -= t;if (y < 0) {y += 7;}y >>= 3;return x + y;
}
M和N的值是多少?
M = 31, N = 8。
关于整数运算的最后思考
计算机执行的“整数”运算实际上是一种模运算,因为整型的有限字长限制了可能的取值范围,运算结果可能溢出。
无符号数与补码数在运算时,拥有相同的位级行为,区别在于编译器解释位的方式。
练习
int x = foo();
int y = bar();
unsigned ux = x;
unsigned uy = y;
对于下面的C表达式,
1)证明对于所有的x和y,结果都为1。
2)给出使他们为0的x和y。
- (x>0)∣∣(x−1<0)(x > 0) || (x - 1 < 0)(x>0)∣∣(x−1<0)
当x = TMin时,结果为0。 - (x & 7) != 7 || (x << 29 < 0)
x的低3位不都是1时,结果是1。
x的低3位都是1时,结果是1。 - (x∗x)>=0(x * x) >= 0(x∗x)>=0
运算可能会溢出,当x = 123456时,x * x的低32位是1000 1100 0111 0101 0001 0000 0000 0000,符号位是1,是负数。 - x<0∣∣−x<=0x < 0 || -x <= 0x<0∣∣−x<=0
如果x是非负数,-x一定是非正的。 - x>0∣∣−x>=0x > 0 || -x >= 0x>0∣∣−x>=0
如果x = TMin,-x还是TMin,都是负数。 - x+y==uy+yxx + y == uy + yxx+y==uy+yx
结果是1。无符号数与补码数有相同的位级行为,且可交换。 - x * ~y + uy * ux == -x
结果是1。
补码表示中,-y = ~ y + 1,因此~ y = -y - 1。
x * ~y + uy * ux = x * (-y - 1) + uy * ux = -xy - x + uy * ux = -x。
相关文章:

【CSAPP】整数运算
文章目录无符号加法练习1练习2补码加法练习1练习2练习3练习4补码的非练习无符号乘法补码乘法练习1练习2练习3乘以常数练习1练习2除以2的幂练习1练习2关于整数运算的最后思考练习无符号加法 考虑两个非负整数x和y,满足0≤x,y<2w0 \le x, y < 2^w0≤x,y<2w&…...
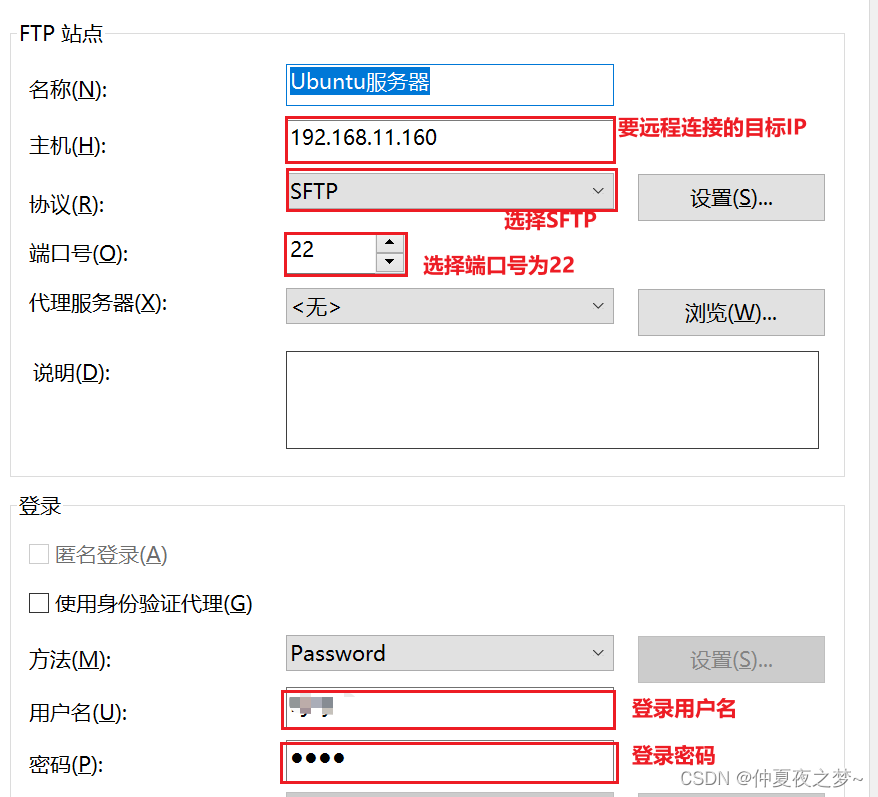
使用 xshell 远程连接(使用 xftp 远程传输)
xshell 和 xftp的使用都基于ssh协议,我们需要先在远程服务端或者虚拟机上安装ssh服务,然后才能远程连接。 目录 1、什么是ssh协议? 2、安装 openssh (1) 安装 openssh 服务器 (2) 关闭服务器防火墙(或者开放端口22)…...

一个例子搞懂子网划分及子网掩码的计算
前置知识: 1、标准ip地址分为A、B、C、D、E五类,分类标准是ip地址的前几个比特位的值。 我们知道ip地址是32位比特-4字节组成,A类地址则是由首位为0,首字节为网络地址,其余3字节为主机地址组成,A类网络地址…...
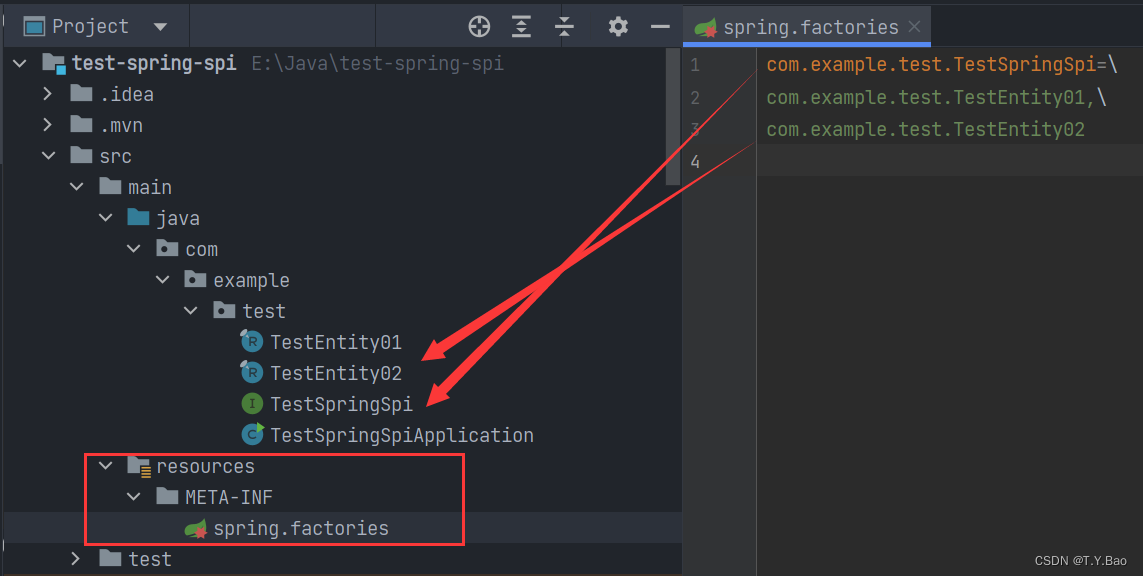
SPI机制源码:JDK Dubbo Spring
JDK 17 Dubbo 3.1.6 JDK SPI JDK SPI在sql驱动类加载、以及slf4j日志实现加载方面有具体实现。 示例 public class Test {private static final Logger logger LoggerFactory.getLogger(Test.class);public static void main(String[] args) {ServiceLoader<JdkSpiServi…...
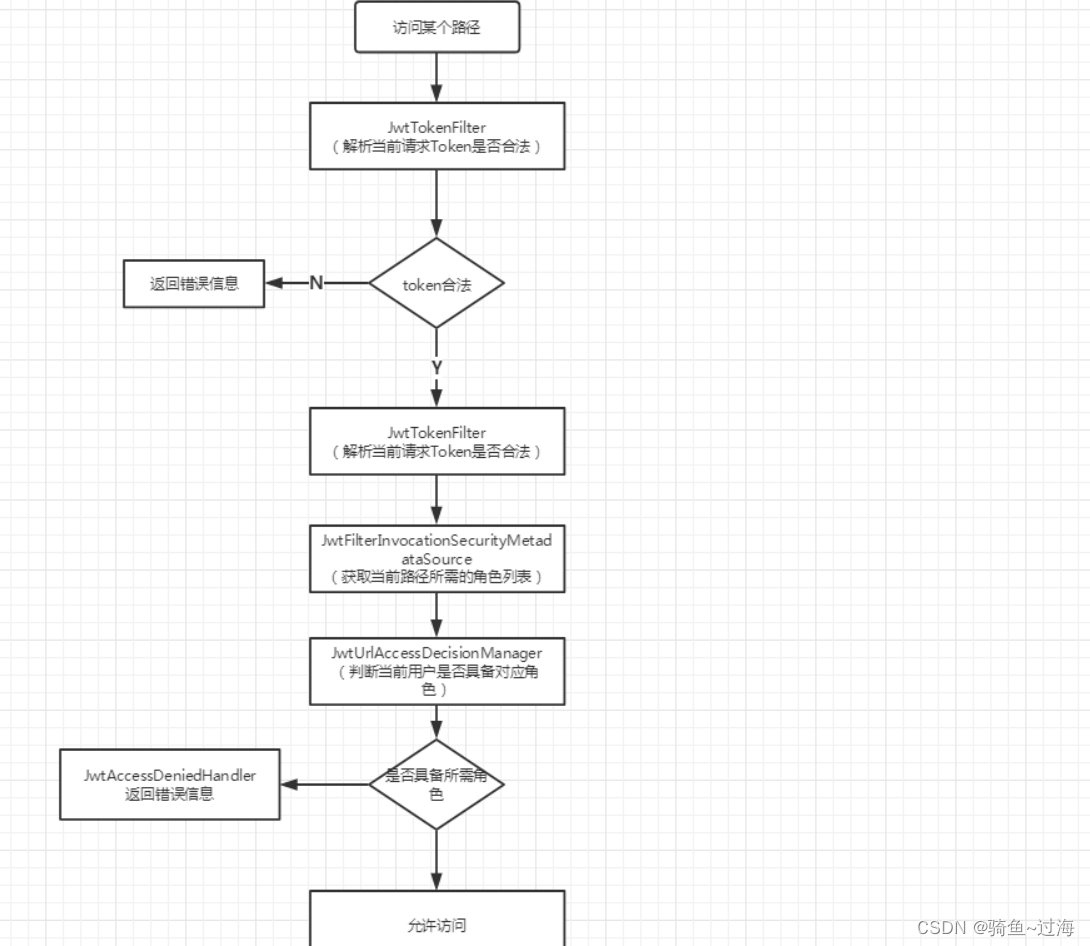
Spring Security+jwt+redis+自定义认证逻辑 权限控制
Spring Securityjwtredis自定义认证逻辑 权限控制 1.拦截访问基本思路 2.创建数据库表:角色表(应该6个表,这里只用用户表代替角色表)、权限表、路径表、角色-权限表、权限-路径表 /* SQLyog Professional v12.14 (64 bit) MySQL…...

打游戏什么蓝牙耳机好用?打游戏比较好的蓝牙耳机
游戏耳机提供身临其境的细致声音,同时也是与朋友在线聊天的绝佳通信设备,尤其对于游戏玩家来说,聆听和被聆听的最佳方式之一就是游戏耳机,那2023年到底有哪些值得购买的游戏耳机呢?现在就让我们一起来看看吧。 第一款…...
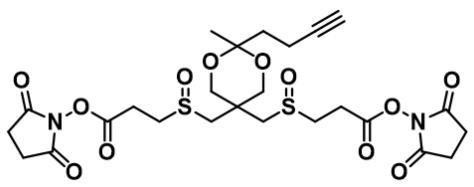
炔基点击交联试剂1704097-05-1,Alkyne-A-DSBSO crosslinker,发生相应点击反应
1、理论分析:中文名:炔基-A-DSBSO crosslinker,英文名:Alkyne-A-DSBSO crosslinkerCAS号:1704097-05-1化学式:C25H32N2O12S2分子量:616.652、产品详情:外观:白色固体&…...
)
刷题记录:牛客NC24309Overplanting (Silver)
传送门:牛客 题目描述: Farmer John has purchased a new machine that is capable of planting grass within any rectangular region of his farm that is "axially aligned" (i.e., with vertical and horizontal sides). Unfortunately, the machine malfunc…...

Spring Boot中使用Sa-Token实现轻量级登录与鉴权
1. Sa-Token 介绍 Sa-Token 是一个轻量级 Java 权限认证框架,主要解决:登录认证、权限认证、单点登录、OAuth2.0、分布式Session会话、微服务网关鉴权 等一系列权限相关问题。 功能结构图 2. 登录认证 对于一些登录之后才能访问的接口(例如&…...
《分布式技术原理与算法解析》学习笔记Day20
CAP理论 什么是CAP理论? CAP理论用来指导分布式系统设计,以保证系统的可用性、数据一致性等。 C,Consistency,一致性,指所有节点在同一时刻的数据是相同的,即更新操作执行结束并响应用户完成后ÿ…...

【2023-2-23】FastDeploy 安装教程
【2023-2-22】FastDeploy 安装编译教程 该测试 FastDeploy CPU版本。 1. fastDeploy库编译 1.1 官方预编译库下载 预编译库下载安装 1.2 自定义CPU版本库编译 官方编译FastDeploy教程 CMakeGUI VS 2019 IDE编译FastDeploy 本人编译教程 CMAKE_CONFIGURATION_TYPES 属性设…...

rollup.js 一个简单实用的打包工具
最近在看vue3相关的知识的时候,发现了一个新的打包工具,至少于我而言是新鲜的。它就是rollup.js。一说到JS打包、合并、压缩、模块处理等都会想到webpack,这是王者,当然入门的难度偏高。而vue3中搭配的vite运行速度确实非常快&…...
数据结构与算法之最小爬楼梯费用动态规划
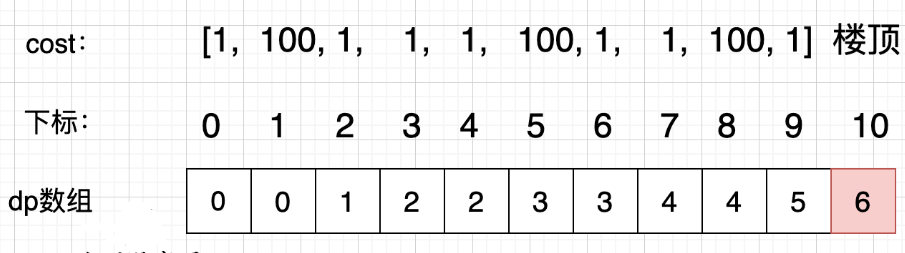
继续上一道题目,在上一道题目的基础之上,我们来解决这一道爬楼梯最小费用题。一.题目描述二.思路(动态规划五部曲)确定dp数组以及下标的含义使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。dp[i]的…...

阿里云ACA认证如何获取?
获取阿里云ACA(Alibaba Cloud Certification Associate)认证,需要按照以下步骤进行操作: 注册阿里云账号。如果您还没有阿里云账号,请先注册一个账号。登录阿里云官网。登录后,进入阿里云认证中心。选择AC…...
【Python入门第十六天】Python If ... Else
Python 条件和 If 语句 Python 支持来自数学的常用逻辑条件: 等于:a b不等于:a ! b小于:a < b小于等于:a < b大于:a > b大于等于:a > b 这些条件能够以多种方式使用,…...

两数之和的解法
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案…...
领导催我优化SQL语句,我求助了ChatGPT。这是ChatGPT给出的建议,你们觉得靠谱吗
作为一个程序员,无论在面试还是工作中,优化SQL都是绕不过去的难题。 为啥?工作之后才会明白,随着公司的业务量增多,SQL的执行效率对程系统运行效率的影响逐渐增大,相对于改造代码,优化SQL语句是…...
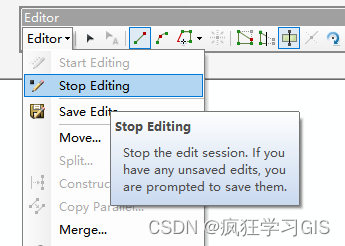
ArcGIS手动分割矢量面要素从而划分为多个面部分的方式:Cut Polygons Tool
本文介绍在ArcGIS下属ArcMap软件中,通过“Cut Polygons Tool”工具,对一个面要素矢量图层加以手动分割,从而将其划分为指定形状的多个部分的方法。 对于一个面要素矢量文件,有时我们需要对其加以划分,通过手动勾勒新的…...

【LeetCode】剑指 Offer 13. 机器人的运动范围 p92 -- Java Version
题目链接:https://leetcode.cn/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/ 1. 题目介绍(13. 机器人的运动范围) 地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动࿰…...

[oeasy]python0091_仙童公司_八叛逆_intel_8080_altair8800_牛郎星
编码进化 个人电脑 计算机 通过电话网络 进行连接 极客 利用技术 做一些有趣的尝试 极客文化 是 认真研究技术的 文化 计算机 不再是 高校和研究机构高墙里面的 神秘事物而是 生活中常见的 家用电器 ibm 蓝色巨人脚步沉重 dec 小型机不断蚕食低端市场甚至组成网络干掉大型机…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
