正则表达式是如何运作的?
在日常的开发工作当中,我们必不可免的会碰到需要使用正则的情况。
正则在很多时候通过不同的组合方式最后都可以达到既定的目标结果。比如我们有一个需要匹配的字符串:
hello
,我们可以通过 /.</p>/ 以及 /
.?</p>/ 来匹配,两种方式就像就像中文语法中的陈述句以及倒装句,不同的语序往往不影响我们的理解,但是他们的运作方式却完全不一样。
为了让大家有一个更加直观的感受,这里将
hello
分三次存到一份百万字符文档的最前面,中间以及最后面,然后分别使用上面的 2 个正则表达式进行匹配,并测算匹配到对应字符所需要的时间,结果如下(实验结果通过 https://regexr.com/ 得出):最前面 中间 最后面
/
.</p>/ 1.1ms 0.7ms 0.2ms
/
.?</p>/ 0.1ms 0.2ms 0.3ms
由此我们可以明显地看出不同的撰写方式,匹配的效率也有很大的不同。
撰写正则是一个不断思考与抉择的过程。就像一道数学题中往往包含一种或几种最优解的可能,想要趋近这个结果,就需要我们理清题意,掌握正则的表达方式以及加强对正则运作方式的理解。
那么,我们应该如何趋近最优解,养成良好的撰写习惯,锻炼撰写健壮的正则表达式的能力呢?
知己知彼,百战不殆,要写好正则表达式就需要做到知其然还要知其所以然。因此,本文将尝试从正则原理的角度出发,介绍正则匹配的规则,梳理正则与有限自动机的关系、及有限自动机之间的转化逻辑,并解释回溯等相关概念。希望能够帮助大家更好地理解及使用正则。
正则表达式与有限自动机(FA)
正则表达式是建立在 有限自动机 ( Finite Automaton ) 的理论基础上的,是自动机理论的应用。当我们写完相关的表达式之后,正则引擎会按照我们所写的表达式构建相应的自动机,若该自动机接受输入的文本并抵达最终状态,则表示输入的文本可以被我们所写的正则表达式匹配到。
有限自动机的图示
自动机的图形化包含以下元素:
箭头:表示路径,可以在上面标注字母,表示状态 1 经过该字母可以转换到状态 2 (也可以是标注 ε,即空串,表示无需经过转换就可以从状态 1 过渡到状态 2),
单圆圈:表示非结束的中间状态
双圆圈:表示结束状态
由自身指向自身的箭头:用于表示 Kleene 闭包(也就是正则表达式中的 ),指可以走任意次数的路径。
以 abc 这条正则表达式为例,其有限自动机的图示如下,表示状态 1 经过 a 可以过渡到状态 2 ,在状态 2 可以经过 ε 再循环经过 b 也可以不经过 b 而直接通过通过 ε 再经由 c 过渡到最终的结束状态。
不确定有限自动机(NFA)及确定有限自动机(DFA)
有限自动机又可以分为 NFA:不确定有限自动机(Nondeterministic Finite Automaton )及 DFA:确定有限自动机(Deterministic Finite Automaton ),NFA 的不确定性表现在其状态可以通过 ε 转换 以及对同一个字符可以有不同的路径。而 DFA 可以看作是一种特殊的 NFA,其最大的特点就是确定性,即输入一个字符,一定会转换到确定的状态,而不会有其他的可能。
以 ab|ac 这条正则表达式为例子,我们可以得到以下 NFA 及 DFA 两种自动机。
可以看到自动机 1 中我们有两条路径都是 a,经由 a 可以到达下一个状态,而自动机 2 中只有一条路径,对于图一来说,经由相同的 a 路径却可以导致不同的结果,这即是 NFA,具有不确定性。而对图二来说,其路径都是通往明确的结果,具有确定唯一性,所以是 DFA。
正则替换成 NFA
从上面的图中我们可以看出 DFA 的匹配路径比 NFA 要少且匹配的速度要更快,但是目前大多数的语言中的正则引擎使用的却是 NFA,为什么不直接使用 DFA 而要使用 NFA?为了解答这个问题,我们需要知道如何通过正则转化成 NFA,而 NFA 又可以怎样转成 DFA。
正则表达式转 NFA 主要基于以下 3 条规则(R 表示正则表达式)
连接 R = AB
选择 R = A|B
重复 R = A*
其他的运算基本都可以通过以上三种运算转换得到,比如 A+ 可以用 AA* 来表示
Thompson 算法
为了更好地理解上面的 3 条转换规则,这里介绍比较实用且容易理解由 C 语言 & Unix 之父之一的 Ken Thompson 提出的 Thompson 算法。其思想主要就是通过简单的表达式组合成复杂的表达式。
Thompson算法 中两种最基本的单元(或者说两种最基本的 NFA):
表示经过字符 a 过渡的下一个状态以及不需要任何字符输入的 ε 转换 过渡到下一个状态。
对于连接运算 R = AB,我们将 AB 拆解成 NFA(A) 与 NFA(B) 两个单元,然后进行组合:
对于选择运算 R = A|B,我们同样将 A 与 B 拆解成 NFA(A) 与 NFA(B) 两个单元,然后进行组合:
对于重复运算 R = A*,其表示可能不需要经过转换,可能经过 1 次或者多次,所以拆解成单一 NFA 后,我们可以这样表示:
由此,我们就可以根据上面的 3 条转换规则,将正则表达式进行拆分重组,最后得出相应的 NFA。
NFA 转换成 DFA 及其简化
DFA 实际上是一个特殊的 NFA,转 DFA,就是要将 NFA 中将所有等价的状态合并,消除不确定性。
这里以《编译原理》一书中的一道例题来完整地讲解一下如何从正则转 NFA 再转成相应的 DFA,并对其进行简化。
eg: (a|b)(aa|bb)(a|b)
这里我们依据正则转 NFA 的三条规则以及 Thompson 算法 的理念,将上述的表达式进行拆分与组合:
首先我们将该表达式以括号为分隔,视为 3 个正则表达式子通过连接符连接,以此拆分成 3 个表达式并将其组合
然后根据每个表达式括号内的内容继续拆分成更细的单元,碰到运算符号,则按照规则进行转换,以此类推直到 NFA 变成变成由最小单元组合而成。
子集构造算法
正如前面所说,NFA 转 DFA 本质是将等价的状态合并,消除不确定性。要找出等价的状态,我们需要先找出各个状态的集合。
上面的表达式只有 a 跟 b 两个字符,所以我们要得出各个状态经过 a 以及经过 b 的所有集合,然后再将等价的集合合并。这里先画出所有集合构成的转换表单,结合图示将更有助于我们的的理解。
I Ia Ib
{i,1,2} {1,2,3} {1,2,4}
{1,2,3} {1,2,3,5,6,f} {1,2,4}
{1,2,4} {1,2,3} {1,2,4,5,6,f}
{1,2,3,5,6,f} {1,2,3,5,6,f} {1,2,4,6,f}
{1,2,4,5,6,f} {1,2,3,6,f} {1,2,4,5,6,f}
{1,2,4,6,f} {1,2,3,6,f} {1,2,4,5,6,f}
{1,2,3,6,f} {1,2,3,5,6,f} {1,2,4,6,f}
图示第一列主要是放置所有不重复的集合,第二列表示经过 a 的集合,第三列表示经过 b 的集合
子集构造法 寻找集合的规则为碰到一个字符,如果这个字符后面有可以通过 空串(ε转换)到达下一个状态,则下一个状态包含在该集合中,一直往后直到碰到一个明确的字符
从上面构造的NFA的初始状态 i 开始,其经过 2 个 ε转换 转换可以到达 2 状态,此后必须经过 a 或者 b,由此我们可以得到第一个状态集合 {i,1,2}
从第一个集合开始,分析集合内分别经过 a 和 b 可以达到什么状态,可以看到初始集合中 i 只经过空串,不经过 a、b, 状态 1 经过 a 可以到达它自身,也可以再经过 ε 到达状态 2,2 经过 a 只能到达状态 3
据此我们得到初始集合经过 a 的集合为 {1,2,3},同样的,初始集合经过 b 只在状态 2 与经过 a 不同,所以我们可以得到经过 b 的集合为 {1,2,4}
因为 {1,2,3},{1,2,4} 都没有出现过,所以这里我们将其记到第一列的第二与第三行,并分析它们经过 a 与 b 的集合。
以此类推直到获得上述所有集合构成的转换表单(完整文字版推导过程附于文末附录)
可以看到上面的转换表的第一列中一共有 7 个集合,这里我们给第一列的集合进行排序(为方便与 NFA 对比,这里将序号 0 改为 i),并对右边经过 a 跟经过 b 的所有集合根据左边的序号进行标记,可以得到相应转换矩阵:
I Ia Ib
{i,1,2} i {1,2,3} 1 {1,2,4} 2
{1,2,3} 1 {1,2,3,5,6,f} 3 {1,2,4} 2
{1,2,4} 2 {1,2,3} 1 {1,2,4,5,6,f} 4
{1,2,3,5,6,f} 3 {1,2,3,5,6,f} 3 {1,2,4,6,f} 5
{1,2,4,5,6,f} 4 {1,2,3,6,f} 6 {1,2,4,5,6,f} 4
{1,2,4,6,f} 5 {1,2,3,6,f} 6 {1,2,4,5,6,f} 4
{1,2,3,6,f} 6 {1,2,3,5,6,f} 3 {1,2,4,6,f} 5
转换矩阵
S a b
i 1 2
1 3 2
2 1 4
3 3 5
4 6 4
5 6 4
6 3 5
依据转换矩阵,我们把第一列的数据作为每一个单独状态,并以 i 为初始状态,由矩阵可得,其经过 a 可以到达状态 1,经过 b 可以到达状态 2,同时我们将包含 f 的集合作为终态(即序号 3,4,5,6),以此类推,我们可以得到如下的 NFA:
因为该 NFA 不包含空串,也没有由一个状态分出两条相同的分支路径,所以该 NFA 就是上述表达式的 DFA。但该 DFA 看起来还比较复杂,所以我们还需要对其进一步简化。
Hopcroft 算法化简
Hopcroft 算法 是1986年图灵奖获得者 John Hopcroft 所提出的,其本质思想跟子集构造法相似,都是对等价状态的合并。
Hopcroft 算法 首先将未化简的 DFA 划分成 终态集 和 非终态集(因为这两种状态一定不等价),之后不断进行划分,直到不再发生变化。每轮划分对所有子集进行。对一个子集的划分中,若每个输入符号都能把状态转换到等价的状态,则两个状态等价。
这里依据 Hopcroft 算法 将上述 DFA 以终态以及非终态进行划分,可以得到 {i,1,2} 以及 {3,4,5,6} 两个集合。然后分别分析两个集合是否能够进一步划分。
集合 {i,1,2} 经过 a 可以得到状态 1 和 3,3 不在集合 {i,1,2} 中,依据矩阵图,我们可以看到 i 和 2 经过 a 都到状态 1,1 经过 a 可以达到状态 3,于是我们将 {i,1,2} 划分成 {i,2} 和 {1} 两个集合
因为 {1} 已经是最小集合,所以无法继续划分,所以分析 {i,2} 集合经过 b 的情况,{i,2} 经过 b 可以达到状态 2 和 4,4 同样不在集合中,所以需要对 {i,2} 进行划分,依据矩阵表,我们可以划分成 {i},{2},至此,非终态已经无法往下拆分,所以分析结束,我们得到的拆分集合为 {i},{1},{2}
终态集合 {3,4,5,6} 经过 a 可以达到状态 3 和 6,3 和 6 都在集合内部,所以无需往下拆分,经过 b 可以达到状态 4 和 5,4 和 5 同样都在集合内,无需拆分。所以我们可以将 {3,4,5,6} 当作是一个整体。
将集合 {3,4,5,6} 当作一个整体,记成状态 3,重新梳理上面的矩阵,并将所有指向 3,4,5,6 的路径都指向新的状态 3,我们可以得到新的也是最简单的 DFA:
从上面的转换过程可以看到,实际上,NFA 转 DFA 是一个繁琐的过程,如果正则采用 DFA 引擎,势必会消耗部分性能在 NFA 的转换上,而这个转换的效益很多时候远不比直接用使用 NFA 高效,同时 DFA 相对来说没有 NFA 直观,可操作空间也要比 NFA 少,所以大多数语言的采用 NFA 作为正则的引擎。
回溯
正则采用的是 NFA 引擎,那么我们就必须面对它的不确定性,体现在正则上就是 回溯 的发生。
遇到一个字符串,NFA 拿着正则表达式去比对文本,拿到一个字符,就把它与字符串做比较,如果匹配就记住并继续往下拿下一个字符,如果后面拿到的字符与字符串不匹配,则将之前记下的字符一个个往回退直到上一次出现岔路的地方。
假设现在有一个正则表达式 ab|ac,需要匹配字符串 ac。则 NFA 会先拿到正则的字符 a,然后去比较字符串 ac,发现匹配中了 a,则会去拿下一个字符 b,然后再匹配字符串,发现不匹配,则回溯,吐出字符 b,回到字符 a,取字符 c 去匹配字符串,发现匹配,完成比对。
文字或许比较枯燥,这里用下面得图示来表示上述的过程,蓝色圆圈表示NFA拿到正则的字符后去匹配字符串看是否可以过渡到下一个状态,同时字符的颜色变化表示是否可以被匹配中:

贪婪模式与惰性模式对比
回到一开始讲的通过 /
.</p>/ 以及 /
.?</p>/ 来匹配
hello
的问题,因为量词的特殊性以及 回溯 的存在,所以2种方式的匹配效率也不一样。- 表示重复零次或多次,一般情况下会以 贪婪模式 尽可能地匹配多次,因此在上面的匹配过程中,它会在匹配到
之后一口气把之后的字符也吞并掉,然后通过回溯匹配 < 字符直到匹配到完整的 </p>,而当我们给 * 加上 ? 之后,它就变成非贪婪的 惰性模式,当匹配到
之后它就会通过回溯逐步去匹配 </p> 直到匹配中完整的字符串。
目标字符串:
hello
在两个表达式下的匹配过程:表达式:/
.</p>/ 表达式:/
.?</p>/
< 匹配 < < 匹配 <
表达式:ab
aaa 匹配 a
aaa 匹配 b
aa 回溯
aa 匹配 b
a 回溯
a 匹配 b
回溯
这个正则表达式回溯到最后也没有匹配到对应的字符串,而通常我们所写的正则并不单单像例子中只回溯这一小部分,设想一下,一个需要多处回溯的正则表达式子,去匹配成百上千甚至上万个字符,那对机器来说是多么可怕的一件事情。https://www.ixigua.com/7202959346417074688
相关文章:

正则表达式是如何运作的?
在日常的开发工作当中,我们必不可免的会碰到需要使用正则的情况。 正则在很多时候通过不同的组合方式最后都可以达到既定的目标结果。比如我们有一个需要匹配的字符串: hello,我们可以通过 / .</p>/ 以及 / .?</p>/ 来匹配&…...

JVM参数GC线程数ParallelGCThreads设置
1. ParallelGCThreads参数含义JVM垃圾回收(GC)算法的两个优化标的:吞吐量和停顿时长。JVM会使用特定的GC收集线程,当GC开始的时候,GC线程会和业务线程抢占CPU时间,吞吐量定义为CPU用于业务线程的时间与CPU总消耗时间的比值。为了承…...

java 线程的那些事
什么是进程: 你把它理解成一个软件 什么是线程: 你把它理解成软件里面的一个功能,做的事情 什么是多线程: 你把它理解成 软件里面的某一个功能,原先是一个人累死累活的在那里完成,现在好了,多…...
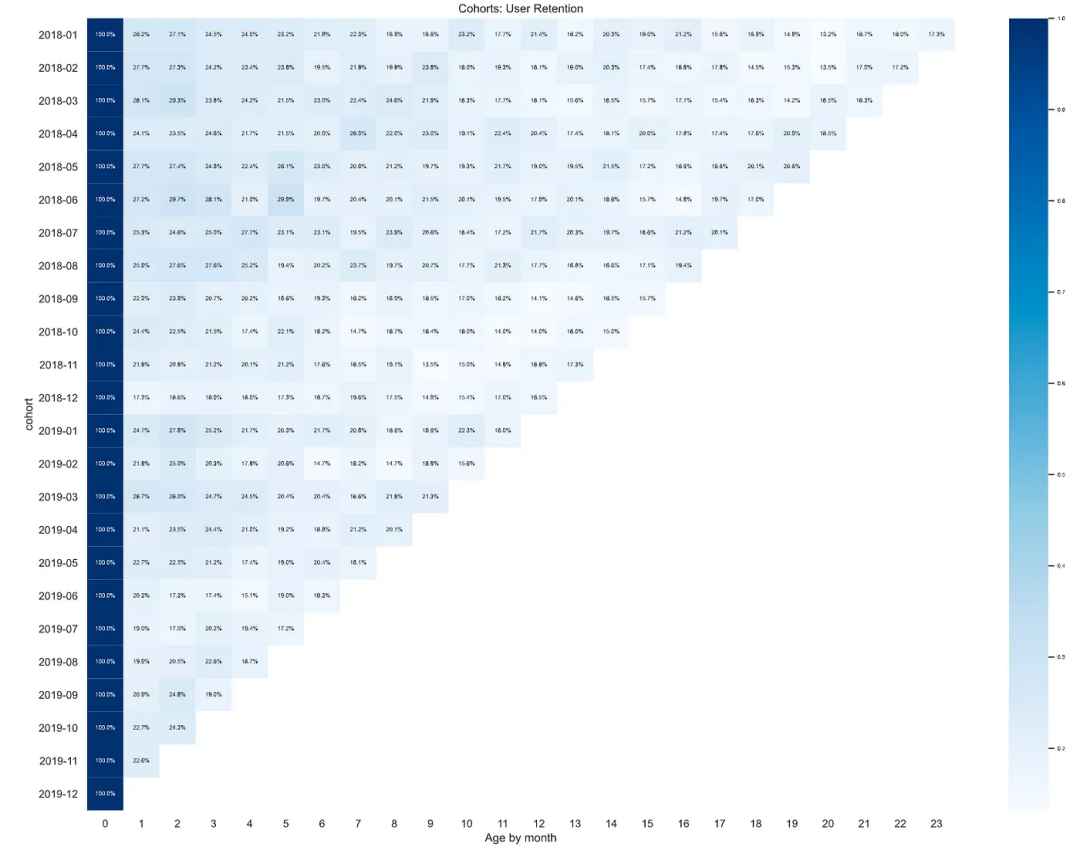
如何利用 Python 进行客户分群分析(附源码)
每个电子商务数据分析师必须掌握的一项数据聚类技能 如果你是一名在电子商务公司工作的数据分析师,从客户数据中挖掘潜在价值,来提高客户留存率很可能就是你的工作任务之一。 然而,客户数据是巨大的,每个客户的行为都不一样。20…...

D1s RDC2022纪念版开发板开箱评测及点屏教程
作者new_bee 本文转自:https://bbs.aw-ol.com/topic/3005/ 目录 芯片介绍开发板介绍RT-Smart用户态系统编译使用感想引用 1. 芯片介绍 RISC-V架构由于其精简和开源的特性,得到业界的认可,近几年可谓相当热门。操作系统方面有RT-Thread&am…...

了解一下TCP/IP协议族
在《简单说说OSI网络七层模型》中讲到,目前实际使用的网络模型是 TCP/IP 模型,它对 OSI 模型进行了简化,只包含了四层,从上到下分别是应用层、传输层、网络层和链路层(网络接口层),每一层都包含…...

【第十九部分】存储过程与存储函数
【第十九部分】存储过程与存储函数 文章目录【第十九部分】存储过程与存储函数19. 存储过程与存储函数19.1 存储过程19.2 创建、调用存储过程19.2.1 不带参数19.2.2 IN 类型19.2.3 OUT类型19.2.4 IN和OUT类型同时使用19.2.5 INOUT类型19.3 存储函数19.4 创建、调用存储函数19.5…...

字节序
字节序 字节序:字节在内存中存储的顺序。 小端字节序:数据的高位字节存储在内存的高位地址,低位字节存储在内存的低位地址 大端字节序:数据的低位字节存储在内存的高位地址,高位字节存储在内存的低位地址 bit ( 比特…...
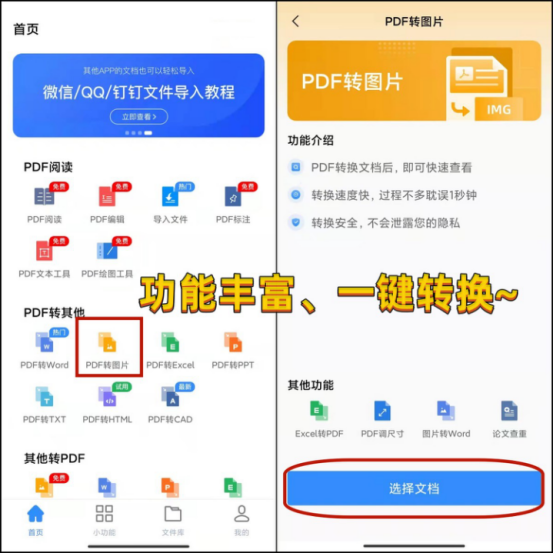
PDF文件怎么转图片格式?转换有技巧
PDF文件有时为了更美观或者更直观的展现出效果,我们会把它转成图片格式,这样不论是归档总结还是存储起来都会更为高效。有没有合适的转换方法呢?这就来给你们罗列几种我个人用过体验还算不错的方式,大家可以拿来参考一下哈。1.用电…...
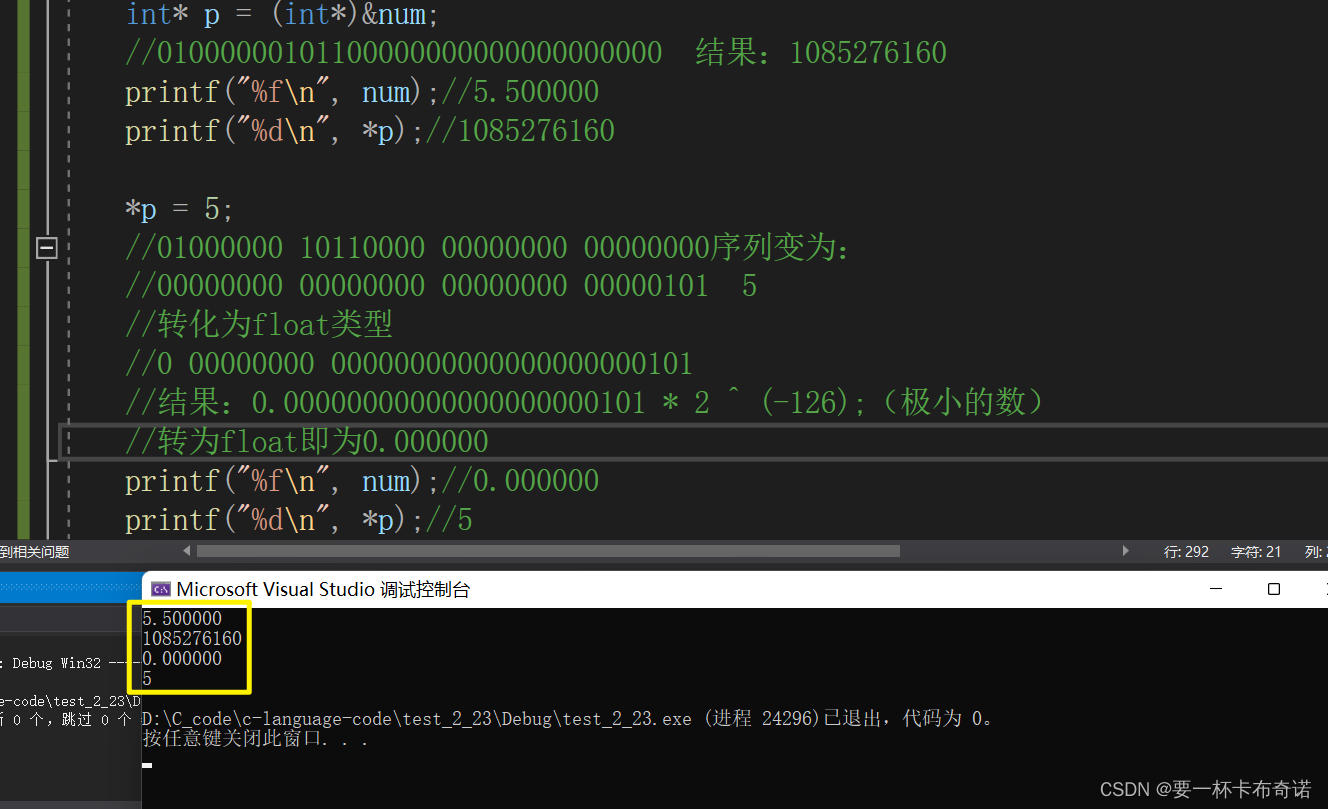
筑基七层 —— 数据在内存中的存储?拿来吧你
目录 零:移步 一.修炼必备 二.问题思考 三.整型在内存中的存储 三.大端字节序和小端字节序 四.浮点数在内存中的存储 零:移步 CSDN由于我的排版不怎么好看,我的有道云笔记相当的美观,请移步至有道云笔记 一.修炼必备 1.入门…...
Typecho COS插件实现网站静态资源存储到COS,降低本地存储负载
Typecho 简介Typecho 是一个简单、强大的轻量级开源博客平台,用于建立个人独立博客。它具有高效的性能,支持多种文件格式,并具有对设备的响应式适配功能。Typecho 相对于其他 CMS 还有一些特殊优势:包括可扩展性、不同数据库之间的…...
2月23号作业
题目:题目一:通过操作Cortex-A7核,串口输入相应的命令,控制LED灯进行工作--->上传CSDN 1.例如在串口输入led1on,开饭led1灯点亮 2.例如在串口输入led1off,开饭led1灯熄灭 3.例如在串口输入led2on,开饭led2灯点亮 4.例如在串口输…...
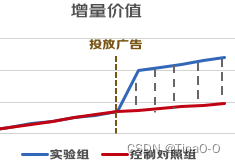
因果推断方法(一)合成控制
知道的跳过下面的简单介绍: 就是比如广告主投放了10w元,那么他的收益怎么算?哪些订单就是广告带来的,哪些是不放广告也会购买? 合成控制法是目前我实际应用发现最好用的。置信度高,且容易理解。 简单讲下思…...
)
数据结构第12周 :( 有向无环图的拓扑排序 + 拓扑排序和关键路径 + 确定比赛名次 + 割点 )
目录有向无环图的拓扑排序拓扑排序和关键路径确定比赛名次割点有向无环图的拓扑排序 【问题描述】 由某个集合上的一个偏序得到该集合上的一个全序,这个操作被称为拓扑排序。偏序和全序的定义分别如下:若集合X上的关系R是自反的、反对称的和传递的&…...
)
Linux安装docker(无网)
1. 下载Docker安装包 下载地址:https://download.docker.com/linux/static/stable/x86_64/ 如果服务器可以联网可以通过wget下载安装包 wget https://download.docker.com/linux/static/stable/x86_64/docker-18.06.3-ce.tgz2. 解压安装 tar -zxvf docker-18.06…...

解决JNI操作内核节点出现写操作失败的问题
Android 9.0下,因为采取了SEAndroid/SElinux的安全机制,即使拥有root权限,或者对某内核节点设置为777的权限,仍然无法在JNI层访问。 本文将以用户自定义的内核节点/dev/wf_bt为例,手把手教会读者如何在JNI层获得对该节…...

纵然是在产业互联网的时代业已来临的大背景下,人们对于它的认识依然是短浅的
纵然是在产业互联网的时代业已来临的大背景下,人们对于它的认识依然是短浅的。这样一种认识的最为直接的结果,便是我们看到了各式各样的产业互联网平台的出现。如果一定要找到这些互联网平台的特点的话,以产业端为出发点,无疑是它…...

干翻 nio ,王炸 io_uring 来了 !!(图解+史上最全)
大趋势:全链路异步化,性能提升10倍 随着业务的发展,微服务应用的流量越来越大,使用到的资源也越来越多。 在微服务架构下,大量的应用都是 SpringCloud 分布式架构,这种架构总体上是全链路同步模式。 全链…...
ur3+robotiq ft sensor+robotiq 2f 140+realsense d435i配置rviz,gazebo仿真环境
ur3robotiq ft sensorrobotiq 2f 140realsense d435i配置rviz,gazebo仿真环境 搭建环境: ubuntu: 20.04 ros: Nonetic sensor: robotiq_ft300 gripper: robotiq_2f_140_gripper UR: UR3 reasense: D435i 通过下面几篇博客配置好了ur3、力传…...

ASP.NET Core MVC 项目 AOP之Authorization
目录 一:说明 二:传统鉴权授权的基本配置 三 :角色配置说明 四:策略鉴权授权 五:策略鉴权授权Requirement扩展 总结 一:说明 鉴权:是指验证你是否登录,你登录后的身份是什么。…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...
