递推问题
递推:
在面对一个大任务的时候,有时候我们可以将大任务划分为小任务,再将小任务划分为更小的任务......,直到遇到初始情况,最后由初始情况一直往前推进,最后解决大任务,这就是递推的思想。
递推问题:
例题1.砖块:
由n 个砖块排成一排,从左到右编号依次为 1∼n,砖块分为黑色(B)和白色(W),每次可以改变相邻两个砖块的颜色。问需要多少次将所有砖块变成一种颜色;
如果可以,输出次数与任意一种改变方案(改变n[k]和n[k]时,输出k);
如果不行输出-1。
思路:
首先,我们假设改变p[k]时,p[k+1]一同变换;
每块砖最多只需要改变一次;
最后需要把所有砖变成W或者B,假设全变为W;
从第一块开始,如果第一块不为W,就改变p[k]与p[k+1],一直扫描到第n-1块砖;
如果最后的一块砖为W,则该情况有解,否则无解;
假设全变为B,重复上述操作即可。
代码如下:
string str;//字符//改变字符为对应字符
void update(char &c){c=='W'?c='B':c='W';
}//判断是否能全变为st
bool check(char st,int n){vector<int>res;//变换的位置string s=str;//注意可能判断两次,不能改变str//如果不为st,则改变for(int i=0;i<n-1;i++)if(s[i]!=st){update(s[i]);update(s[i+1]);res.push_back(i);}//如果最后一位是stif (s[n-1]==st){cout<<res.size()<<endl;if(res.size()){for(int i=0;i<res.size();i++)cout<<res[i]+1<<" ";cout<<endl;}return true;}return false;
}int main(){int n;//字符串长度cin>>n>>str;if(!check('W',n)&&!check('B',n))cout<<"-1"<<endl;//如果两种情况都不行return 0;
}
例题2.费解的开关:
25盏灯排成一个5*5的方形,每一个灯有开(1)和关(0)两种状态,每一次可以改变一盏灯的状态,并且这盏灯的上下左右相邻的灯的状态也都会改变,问最少需要几步可以让所有灯都亮。如果超过六步,则输出-1,否则输出次数。
思路:
每盏灯只有该变一次的必要;
我们先枚举第一行灯的状态(只改变第一盏灯);
因为所有的灯都需要点亮,这时我们就根据第一行灯的状态来改变第二行灯的状态,然后根据第二行的状态.......,最后根据第四行的状态来改变第五行;
最后判断最后一行是否全亮,如果全亮则有解,反之无解;
代码如下:
const int N=6;
int g[N][N],tmp[N][N];//灯,并且把灯的状态复制一份
int dx[]={1,0,-1,0},dy[]={0,1,0,-1};void f(int x,int y){//开关(x,y)g[x][y]==0?g[x][y]=1:g[x][y]=0;for(int i=0;i<4;i++){int a=x+dx[i],b=y+dy[i];if(a<0||b>=5||b<0||b>=5)continue;g[a][b]==0?g[a][b]=1:g[a][b]=0;}return;
}//要枚举很多次,每次枚举不能改变原始状态
int main(){memcpy(tmp,g,sizeof g);int res=7;for(int i=0;i<pow(2,5);i++){//二进制枚举,5个二进制位int s=0;//记录改变了几次for(int i=0;i<5;i++)//每次将g重置for(int j=0;j<5;j++)g[i][j]=tmp[i][j];for(int j=0;j<5;j++){//右移j位if(((i>>j)&1)==1){s++;f(0,j);}}for(int k=0;k<4;k++)//枚举前4行for(int u=0;u<5;u++){if(g[k][u]==0){s++;f(k+1,u);}}for(int k=0;k<5;k++)//判断最后一行是否全亮if(g[4][k]==0)s=7;if(s<=6)res=min(s,res);}return 0;}以集合的视角看待一些递推问题:
很多递推问题让我们求的是方法数/数量、最值等问题,我们可以将要求的东西(方法数等)看作是一个集合,将此集合做一个不重不漏的划分,每个子集也可以以同样的方式划分,就可以得到递推式(子集之和、最值等)。
例题1.数楼梯:
楼梯有 N 阶,从一楼开始上楼,上楼可以一步上一阶,也可以一步上二阶。计算共有多少种不同的走法。
思路:
f[i]表示走到i位置的方法数;
f[k] = f[k-1] + f[k-2];
将走到k阶楼梯的方法数看作是一个集合;
因为只能从k-1和k-2的位置走到k,那么我们可以把走到k的方法数这个集合划分为走到第k-1和走到第k-2这两个台阶的方法集合,这时理解f[k] = f[k-1] + f[k-2]的含义就很容易了。
例题2.过河卒:
棋盘上 A点有一个过河卒,需要走到目标 B 点;
卒行走的规则:可以向下、或者向右。同时在棋盘上 C 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”;
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
思路:
f[a][b]表示走到(a,b)的方法数;
f[a][b] = f[a-1][b] + f[a][b-1];
将走到(a,b)点的方法数看做是一个集合;
由于(a,b)只能是(a-1,b)和(a,b-1)走到的,将(a,b)集合不重不漏的划分为两个集合,走到(a,b)的方法数应该是走到(a-1,b)的方法数加上走到(a,b-1)的方法数。那么f[a][b] = f[a-1][b] + d[a][b-1]。
例题3.数字三角形:
给定一个数字三角形,从顶部出发,在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点,一直走到底层,要求找出一条路径,使路径上的数字的和最大。
思路:
g[i][j]表示三角形(i,j)位置的数,f[i][j]表示走到(i,j)点的最大值;
f[i][j] = max( f[i-1][j-1] , f[i-1][j] ) + g[i][j];
将走到(i , j)点的最大值看作是一个集合,那么这个集合可以划分为从左上角走过来和从右上角走过来这两个集合,我们将两个集合取最大值然后加上g[i][j]即可。
相关文章:

递推问题
递推:在面对一个大任务的时候,有时候我们可以将大任务划分为小任务,再将小任务划分为更小的任务......,直到遇到初始情况,最后由初始情况一直往前推进,最后解决大任务,这就是递推的思想。递推问…...

js中强制类型转换Number、parseInt、parseFloat、Boolean、String、toString的使用
文章目录一、Number() 转换为整数二、Number.parseInt() 将字符串转换为整数三、Number.parseFloat() 将字符串转换为浮点数四、Boolean() 转换为布尔值五、String() 转换为字符串六、.toString() 转换为字符串最近在巩固 js 的基础知识,今天复习到了 js 中的数据类…...
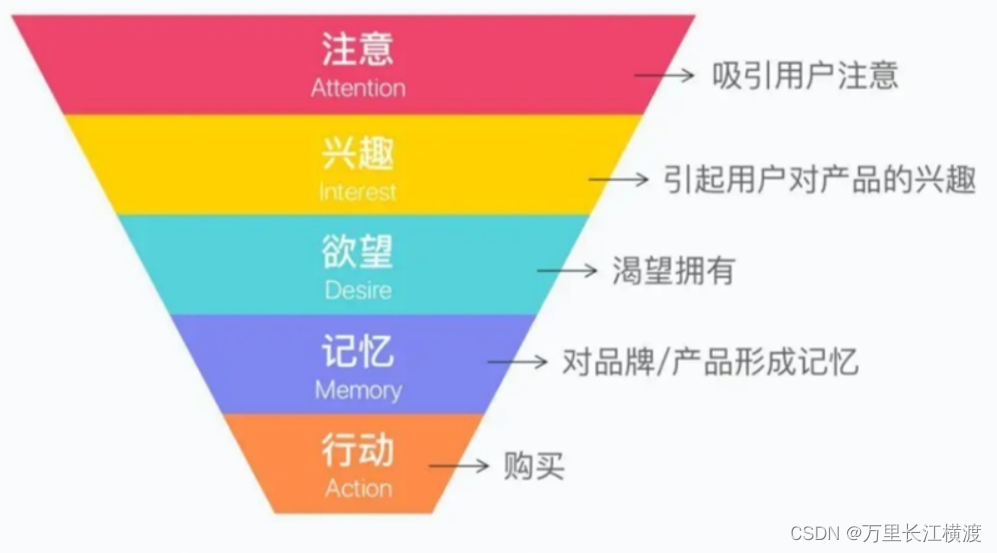
漏斗分析法
一什么是漏斗分析? 漏斗分析是数据领域最常见的一种“程式化”数据分析方法,它能够科学地评估一种业务过程,从起点到终点,各个阶段的转化情况。通过可以量化的数据分析,帮助业务找到有问题的业务环节,并进…...
)
pycharm入门快捷操作(部分)
altenter:提示意图动作shift两次或者crtlshifta:查找框(查找动作、类、项目等)crtlw:一次一个字符、两次整个字符串(if条件下选择整个判断体)、三次整个句子、四次整个引用ctrlshiftw࿱…...

宣布 Databricks 支持 Amazon Graviton2,性价比提高3倍
今天,我们很高兴地宣布 Databricks 对基于 Amazon Graviton2 的亚马逊弹性计算云(Amazon EC2)实例的支持的公开预览。Graviton 处理器由亚马逊云科技进行定制设计和优化,为运行在 Amazon EC2 上的云工作负载提供最佳性价比。当与高…...
18_FreeRTOS任务通知
目录 任务通知的简介 任务通知值的更新方式 任务通知的优势 任务通知的劣势 任务通知值和通知状态 发送通知相关API函数 接收通知相关API函数 任务通知模拟信号量实验 任务通知模拟消息邮箱实验 任务通知模拟事件标志组实验 任务通知的简介 任务通知:用来通知任务的…...

【华为OD机试模拟题】用 C++ 实现 - 整理扑克牌(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...
mysql lesson1
常用命令 1:exit 退出mysql 2:uroot pENTER键,再输入密码,不被别人看见 3:完美卸载:双击安装包,手动删除program file中的mysql,手动删除Programedate里的mysql 4:use mysql 使用数据库 5:…...
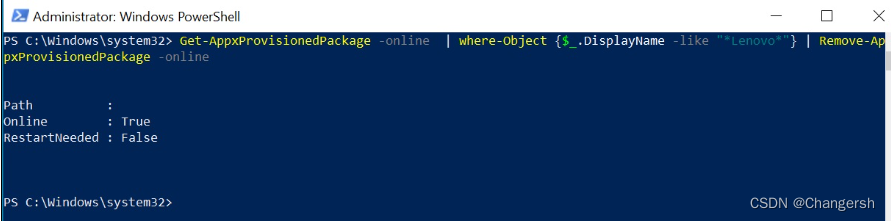
联想笔记本无法下载 Lenovo Vantage
状况 在 Microsoft Store 下载时发生错误,可能是如下代码:0x80070005, 0x80073D05, or 0x80070017. 解决方法 1.在“开始”菜单搜索栏中输入PowerShell 2.当Windows PowerShell出现在“开始”菜单中,右键点击此图标,然后选择以…...

功能性材料深入超级赛道,赋能多行业迭代升级
中国国际胶粘剂及密封剂展览会深耕胶粘剂、密封剂和胶粘带行业26年,是行业认可的、优质的贸易与技术交流平台。展会连接了十几个行业的买家和卖家,包括汽车、电子、新能源、轨道交通、工业等重要领域,为客户提供封装、粘合、散热、装配制造等…...

【项目精选】jsp企业快信系统(论文+视频+源码)
点击下载源码 计算机网络的出现到现在已经经历了翻天覆地的重大改变。因特网也从最早的供科学家交流心得的简单的文本浏览器发展成为了商务和信息的中心。到了今天,互联网已经成为了大量应用的首选平台,人们已经渐渐习惯了网络交易,渐渐对网络…...

通信算法之112:载波同步及comm.CarrierSynchronizer
1. 2. 载波同步是基于锁相环技术使本地获取和载波同频同相的参考信号,用来解调信号。载波同步就是对本地参考信号进行频率和相位偏差的补偿,进而实现本地参考信号和载波信号同频同相。 载波同步只适用于单载波调制系统,载波同步算法对于BPSK、…...
)
【C. Build Permutation】(整数理论、构造、思维)
链接 理论基础 结论:在区间[n,2n]上,至少存在一个完全平方数。结论:在区间[n,2n]上,至少存在一个完全平方数。结论:在区间[n,2n]上,至少存在一个完全平方数。 构造⌈n⌉2构造\lceil \sqrt{n}\rceil^2构造⌈…...
)
前端面试题:事件循环(Eventloop)
什么是事件循环?如何理解事件循环?事件循环原理如何描述?事件循环涉及了很多知识点,想要彻底掌握JS事件循环原理必须要掌握以下知识点:同步任务、异步任务、宏任务、微任务、任务队列、执行栈、js运行机制、EventLoop。 1.事件循…...

jmeter接口自动化测试框架
接口测试可以分为两部分: 一是线上接口(生产环境)自动化测试,需要自动定时执行,每5分钟自动执行一次,相当于每5分钟就检查一遍线上的接口是否正常,有异常能够及时发现,不至于影响用…...
树莓派CM4基础设置
安装系统1.1 软件和硬件准备硬件:CM4(4GB DDR32GB EMMC 板载WIFI和蓝牙)CM4-to-Pi4-Adapter软件:Raspberry Pi或者 Win32DiskImagerRaspberry Pi下载链接:点击直接下载Win32DiskImager下载链接:链接&#x…...

JS 合并数组的三大方式
1. 数组的不可变合并 1.1使用扩展运算符进行合并 如果您想知道一种在JavaScript中合并数组的好方法,那么请记住使用扩展操作符进行合并。 在数组字面量中写入两个或更多带有扩展操作符…前缀的数组,JavaScript将创建一个合并所有这些数组的新数组: co…...
30岁测试开发年薪不足50万,被面试官嘲讽混得太差?
近日,有网友发帖称:“30岁去应聘测试开发,拿不到七八十万的年薪确实有点丢人了,还被面试官diss混得太差了”,网友们看完都炸了。 来看看网友们都是怎么说的。 有网友说: 扯淡 有网友气到: 那拿…...

【C语言】多线程
多线程线程线程的优点C语言多线程创建线程终止线程连接和分离线程开启一个线程最基本的多线程实现开启两个线程多线程进行协同运算无参数传递的线程并发编程实例简单参数传递的线程并发编程实例结构体参数传递的线程并发编程实例线程的连接编程实例信号量同步进行写入互斥信号量…...

CDGA|浅谈“以治促用,以用促治”的数据治理战略
数据治理夯实企业数字化转型基础。采取“以治促用,以用促治”的数据治理战略,可以充分释放了企业核心运行要素的活力。 “以治促用”是指通过建立在数据治理链路及用户多维评估系统的基础上,对数据资产重新进行价值识别,推进高价值…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...

vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能
vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能 查看官网:https://vxetable.cn 效果 代码 通过 checkbox-config.isShift 启用批量选中,启用后按住快捷键和鼠标批量选取 <template><div><vxe-grid v-bind"gri…...

多模态大语言模型arxiv论文略读(110)
CoVLA: Comprehensive Vision-Language-Action Dataset for Autonomous Driving ➡️ 论文标题:CoVLA: Comprehensive Vision-Language-Action Dataset for Autonomous Driving ➡️ 论文作者:Hidehisa Arai, Keita Miwa, Kento Sasaki, Yu Yamaguchi, …...

电脑定时关机工具推荐
软件介绍 本文介绍一款轻量级的电脑自动关机工具,无需安装,使用简单,可满足定时关机需求。 工具简介 这款关机助手是一款无需安装的小型软件,文件体积仅60KB,下载后可直接运行,无需复杂配置。 使用…...
