【数据结构】—堆详解(手把手带你用C语言实现)

食用指南:本文在有C基础的情况下食用更佳
🔥这就不得不推荐此专栏了:C语言
♈️今日夜电波:水星—今泉愛夏
1:10 ━━━━━━️💟──────── 4:23
🔄 ◀️ ⏸ ▶️ ☰
💗关注👍点赞🙌收藏您的每一次鼓励都是对我莫大的支持😍
目录
❤️什么是堆?
堆的分类
💛堆的实现思路
使用什么实现?
怎么分辨父节点以及子节点?
总体实现思路
💜堆的实现
结构体以及接口的实现
💯堆的两种建堆方式(调整方法)究极无敌重要!!!
向上调整方法
向下调整方法
堆的构建
堆的销毁
堆的插入
⭕️堆的删除 (较重要)
取堆顶的数据
堆的数据个数
堆的判空
💚总体代码
❤️什么是堆?
堆是一种基于树结构的数据结构,它是一棵二叉树,具有以下两个特点:
1. 堆是一个完全二叉树,即除了最后一层,其他层都是满的,最后一层从左到右填满。
2. 堆中每个节点都满足堆的特性,即父节点的值要么等于或者大于(小于)子节点的值。
堆的分类
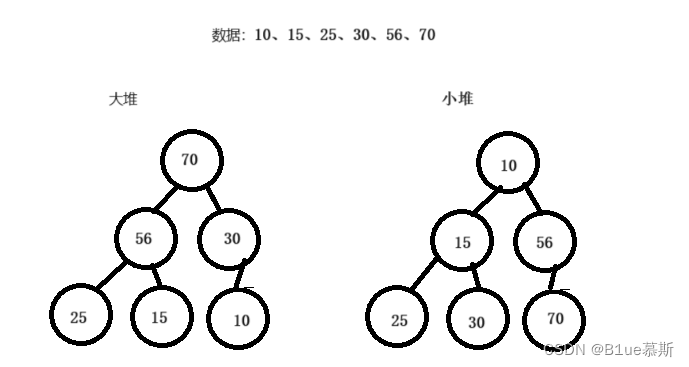
堆一般分为两类:大堆和小堆。大堆中,父节点的值大于或等于子节点的值,而小堆中,父节点的值小于或等于子节点的值。堆的主要应用是在排序和优先队列中。
以下分别为两个堆(左大堆,右小堆):
💛堆的实现思路
使用什么实现?
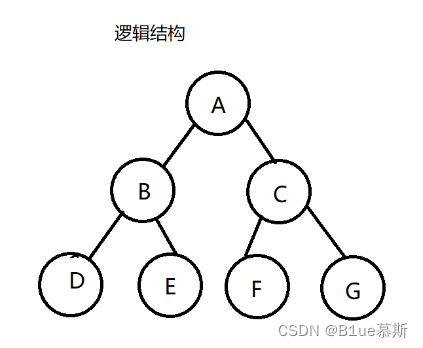
逻辑结构如上, 然而这仅仅是我们想像出来的而已,而实际上的堆的物理结构是一个完全二叉树,通常是用数组实现的。如下:
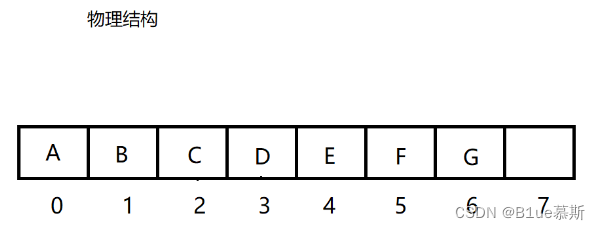
对此,这就要引申出一个问题?我们该如何分辨父节点以及子节点呢?如下:
怎么分辨父节点以及子节点?
通常我们的数组下标为“0”处即为根节点,也就是说我们一定知道一个父节点!并且我们也有计算公式一个来计算父节点以及子节点(先记住,后面实现有用!!!)也就是说我们也可以通过公式从每一个位置计算父节点以及子节点!如下:
总体实现思路
先建立一个结构体,由于堆的结构实际上是一颗完全二叉树,因此我们的结构跟二叉树一样即可!接着,想想我们的堆需要实现的功能?构建、销毁、插入、删除、取堆顶的数据、取数据个数、判空。(⊙o⊙)…基本的就这些吧哈~
接着按照 定义函数接口->实现各个函数功能->测试测试->收工(-_^) o(* ̄▽ ̄*)ブ
💜堆的实现
结构体以及接口的实现
typedef int HPDataType;typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
💯堆的两种建堆方式(调整方法)究极无敌重要!!!
在实现以上的接口之前,我们必须必须要知道堆的两种建堆方式!!!
并且仅仅通过调整两种建堆方式的<和>符号我们就可以轻易控制大小堆,具体看代码注释!
建堆有两种方式,分别是自底向上建堆以及自顶向下建堆。具体简介如下:
1. 自底向上建堆:自底向上建堆是指按照原始数组顺序依次插入元素,然后对每个插入的元素执行向上调整的操作,使得堆的性质保持不变。这种方法需要对每个元素都进行调整操作,时间复杂度为 O(nlogn)。
2. 自顶向下建堆:自顶向下建堆是指从堆顶开始,对每个节点执行向下调整操作,使得堆的性质保持不变。这种方法需要从根节点开始递归向下调整,时间复杂度为 O(n)。因此,自顶向下建堆的效率比自底向上建堆要高。
以上两种建堆方式 实际上是基于两种调整方法,接下来将详细介绍:
向上调整方法
堆的向上调整方法将新插入的节点从下往上逐层比较,如果当前节点比其父节点大(或小,根据是大根堆还是小根堆),则交换这两个节点。一直向上比较,直到不需要交换为止。这样可以保证堆的性质不变。
具体步骤如下:
1.将新插入的节点插入到堆的最后一位。
2.获取该节点的父节点的位置,比较该节点与其父节点的大小关系。
.如果该节点比其父节点大(或小,根据是大根堆还是小根堆),则交换这两个节点。
4.重复步骤2-3,直到不需要交换为止,堆的向上调整完成。
堆的向上调整的时间复杂度为O(logn),其中n为堆的大小。
一图让你了解~(以大堆为例)

实现如下:
void swap(HPDataType* s1, HPDataType* s2)
{HPDataType temp = *s1;*s1 = *s2;*s2 = temp;
}void Adjustup(HPDataType* a, int child)//向上调整
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent])//建大堆,小堆则<{swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}向下调整方法
堆的向下调整方法是指将某个节点的值下放至其子节点中,以维护堆的性质的过程。
假设当前节点为 i,其左子节点为 2i+1,右子节点为 2i+2,堆的大小为 n
则向下调整的步骤如下:
-
从当前节点 i 开始,将其与其左右子节点中较小或较大的节点比较,找出其中最小或最大的节点 j。
-
如果节点 i 小于等于(或大于等于,取决于是最小堆还是最大堆)节点 j,则说明它已经满足堆的性质,调整结束;否则,将节点 i 与节点 j 交换位置,并将当前节点 i 更新为 j。
-
重复执行步骤 1 和步骤 2,直到节点 i 没有子节点或已经满足堆的性质。
一图让你了解~(以大堆为例)

实现如下:
void swap(HPDataType* s1, HPDataType* s2)
{HPDataType temp = *s1;*s1 = *s2;*s2 = temp;
}void Adjustdown(HPDataType* a, int n, int parent)//向下调整
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child])//找出两个孩子中较大的那个,此为大堆,如果要实现小堆则 改 >{++child;}if (a[child] > a[parent])//此为大堆,如果要实现小堆则 改 >{swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n)
{assert(hp);assert(a);hp->_a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (!hp->_a){perror("malloc fail");exit(-1);}hp->_capacity = hp->_size = n;//将a中的元素全部转移到堆中memcpy(hp->_a, a, sizeof(HPDataType) * n);//建堆for (int i = 1; i < n; i++){Adjustup(hp->_a, i);//按向上调整,此建立大堆}}本文的构建方法是通过传递一个数组以及传递一个数组大小来构建的,里面包括了堆结构体的初始化操作,基本的建堆方式则是通过向上调整方法建堆。
堆的销毁
void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}就正常的销毁操作?大家应该都懂(确信) (o°ω°o)
堆的插入
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);if (hp->_capacity == hp->_size)//扩容{int newcapacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;HPDataType* new = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * newcapacity);if (!new){perror("realloc fail");exit(-1);}hp->_a = new;hp->_capacity = newcapacity;}hp->_a[hp->_size++] = x;Adjustup(hp->_a, hp->_size - 1);}实现是对于堆的空间进行判断,不够则是扩容操作,当然也有初始化的意思,接着是通过向上调整的方式插入操作。
⭕️堆的删除 (较重要)
void HeapPop(Heap* hp)//先将最后一个数与堆顶交换,然后再让size--,再进行向下调整
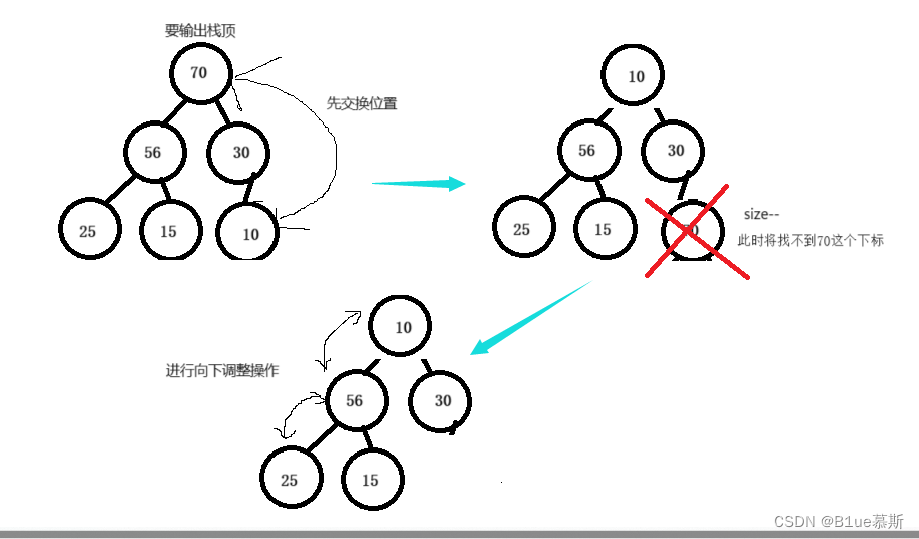
{assert(hp);swap(&hp->_a[0], &hp->_a[hp->_size - 1]);hp->_size--;Adjustdown(hp->_a, hp->_size, 0);}进行删除操作,我们当然是删除堆顶啦,这个删除操作先将最后一个数与堆顶交换,然后再让size--,再进行向下调整。
一图让你了解~
取堆顶的数据
HPDataType HeapTop(Heap* hp)//取堆顶
{assert(hp);assert(hp->_size > 0);return hp->_a[0];
}
堆的数据个数
int HeapSize(Heap* hp)//堆大小
{assert(hp);return hp->_size;
}堆的判空
int HeapEmpty(Heap* hp)//判堆空
{assert(hp);return hp->_size==0;
}💚总体代码
pile.h
#pragma once
#define _CRT_SECURE_NO_WARNINGS 01
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<assert.h>typedef int HPDataType;typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);pile.c
#include"pile.h"void swap(HPDataType* s1, HPDataType* s2)
{HPDataType temp = *s1;*s1 = *s2;*s2 = temp;
}void Adjustup(HPDataType* a, int child)//向上调整
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent])//建大堆,小堆则<{swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void Adjustdown(HPDataType* a, int n, int parent)//向下调整
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child])//找出两个孩子中较大的那个,此为大堆,如果要实现小堆则 改 >{++child;}if (a[child] > a[parent])//此为大堆,如果要实现小堆则 改 >{swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapCreate(Heap* hp, HPDataType* a, int n)
{assert(hp);assert(a);hp->_a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (!hp->_a){perror("malloc fail");exit(-1);}hp->_capacity = hp->_size = n;//将a中的元素全部转移到堆中memcpy(hp->_a, a, sizeof(HPDataType) * n);//建堆for (int i = 1; i < n; i++){Adjustup(hp->_a, i);//按向上调整,此建立大堆}}void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}void HeapPush(Heap* hp, HPDataType x)
{assert(hp);if (hp->_capacity == hp->_size)//扩容{int newcapacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;HPDataType* new = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * newcapacity);if (!new){perror("realloc fail");exit(-1);}hp->_a = new;hp->_capacity = newcapacity;}hp->_a[hp->_size++] = x;Adjustup(hp->_a, hp->_size - 1);}void HeapPop(Heap* hp)//先将最后一个数与堆顶交换,然后再让size--,再进行向下调整
{assert(hp);swap(&hp->_a[0], &hp->_a[hp->_size - 1]);hp->_size--;Adjustdown(hp->_a, hp->_size, 0);}HPDataType HeapTop(Heap* hp)//取堆顶
{assert(hp);assert(hp->_size > 0);return hp->_a[0];
}int HeapSize(Heap* hp)//堆大小
{assert(hp);return hp->_size;
}int HeapEmpty(Heap* hp)//判堆空
{assert(hp);return hp->_size==0;
}test.c
#include"pile.h"void test()
{Heap hp;int arr[] = { 1,6,2,3,4,7,5 };HeapCreate(&hp, arr, sizeof(arr) / sizeof(arr[0]));//HeapPush(&hp, 10);printf("%d\n", HeapSize(&hp));while (!HeapEmpty(&hp)){printf("%d %d \n", HeapTop(&hp), HeapSize(&hp));HeapPop(&hp);}printf("%d\n", HeapSize(&hp));HeapDestory(&hp);HeapSort(arr, sizeof(arr) / sizeof(arr[0]));printf("\n");
}int main()
{test();return 0;
}测试结果:

感谢你耐心的看到这里ღ( ´・ᴗ・` )比心,如有哪里有错误请踢一脚作者o(╥﹏╥)o!

给个三连再走嘛~
相关文章:

【数据结构】—堆详解(手把手带你用C语言实现)
食用指南:本文在有C基础的情况下食用更佳 🔥这就不得不推荐此专栏了:C语言 ♈️今日夜电波:水星—今泉愛夏 1:10 ━━━━━━️💟──────── 4:23 …...

关于算法复杂度的几张表
算法在改进今天的计算机与古代的计算机的区别 去除冗余 数据点 算法复杂度 傅里叶变换...
蓝桥杯每日一题2023.10.1
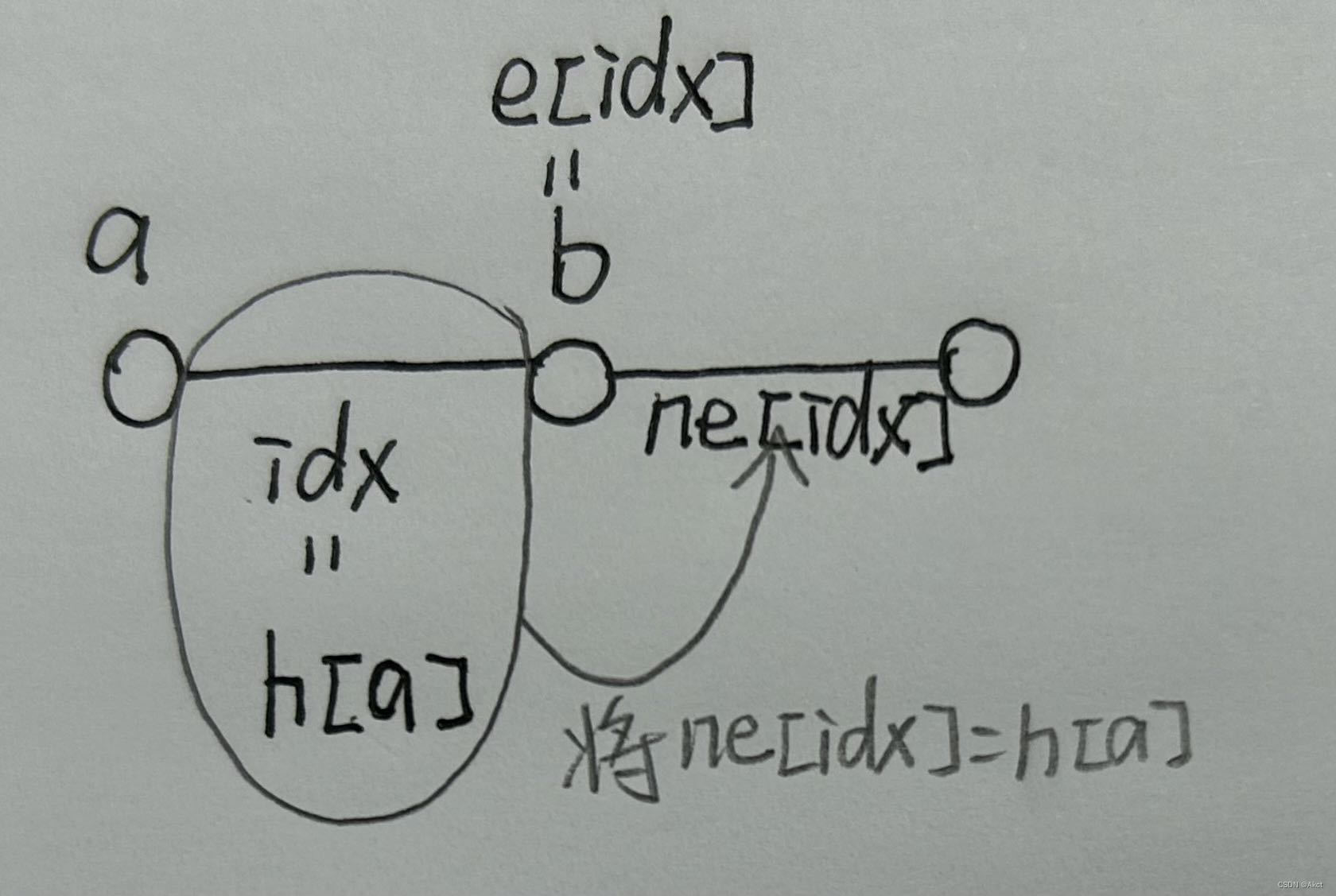
路径 - 蓝桥云课 (lanqiao.cn) 题目分析 求最短路问题,有多种解法,下面介绍两种蓝桥杯最常用到的两种解法 方法一 Floyd(求任意两点之间的最短路)注:不能有负权回路 初始化每个点到每个点的距离都为0x3f这样才能对…...
)
第三章:最新版零基础学习 PYTHON 教程(第十节 - Python 运算符—Python 中的运算符重载)
运算符重载意味着赋予超出其预定义操作含义的扩展含义。例如,运算符 + 用于添加两个整数以及连接两个字符串和合并两个列表。这是可以实现的,因为“+”运算符被 int 类和 str 类重载。您可能已经注意到,相同的内置运算符或函数对于不同类的对象显示不同的行为,这称为运算符…...
)
Nacos 实现服务平滑上下线(Ribbon 和 LB)
前言 不知道各位在使用 SpringCloud Gateway Nacos的时候有没有遇到过服务刚上线偶尔会出现一段时间的503 Service Unavailable,或者服务下线后,下线服务仍然被调用的问题。而以上问题都是由于Ribbon或者LoadBalancer的默认处理策略有关,其…...

c/c++里 对 共用体 union 的内存分配
对union 的内存分配,是按照最大的那个成员分配的。 谢谢...
博途SCL区间搜索指令(判断某个数属于某个区间)
S型速度曲线行车位置控制,停靠位置搜索功能会用到区间搜索指令,下面我们详细介绍区间搜索指令的相关应用。 S型加减速行车位置控制(支持点动和停车位置搜索)-CSDN博客S型加减速位置控制详细算法和应用场景介绍,请查看下面文章博客。本篇文章不再赘述,这里主要介绍点动动和…...
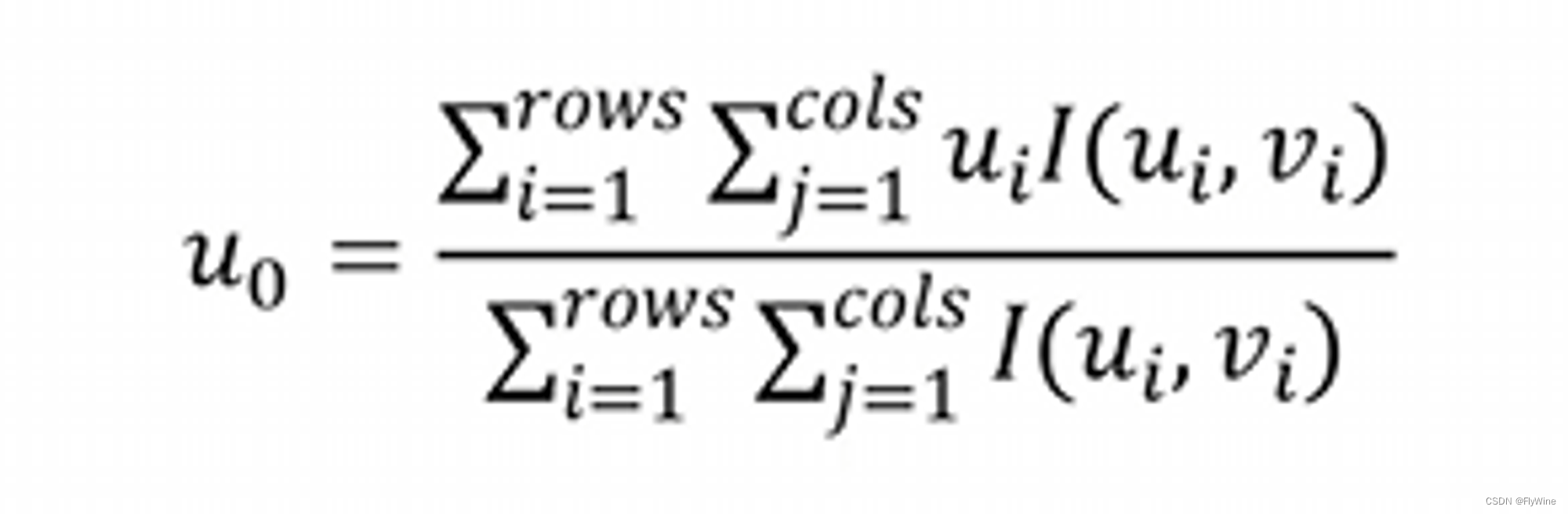
(三)激光线扫描-中心线提取
光条纹中心提取算法是决定线结构光三维重建精度以及光条纹轮廓定位准确性的重要因素。 1. 光条的高斯分布 激光线条和打手电筒一样,中间最亮,越像周围延申,光强越弱,这个规则符合高斯分布,如下图。 2. 传统光条纹中心提取算法 传统的光条纹中心提取算法有 灰度重心法、…...
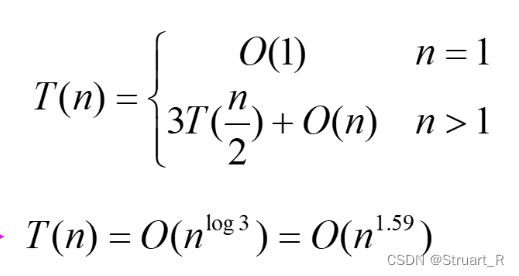
递归与分治算法(1)--经典递归、分治问题
目录 一、递归问题 1、斐波那契数列 2、汉诺塔问题 3、全排列问题 4、整数划分问题 二、递归式求解 1、代入法 2、递归树法 3、主定理法 三、 分治问题 1、二分搜索 2、大整数乘法 一、递归问题 1、斐波那契数列 斐波那契数列不用过多介绍,斐波那契提出…...
Java之SpringCloud Alibaba【六】【Alibaba微服务分布式事务组件—Seata】
一、事务简介 事务(Transaction)是访问并可能更新数据库中各种数据项的一个程序执行单元(unit)。 在关系数据库中,一个事务由一组SQL语句组成。 事务应该具有4个属性: 原子性、一致性、隔离性、持久性。这四个属性通常称为ACID特性。 原子性(atomicity) ∶个事务…...
Android逆向学习(五)app进行动态调试
Android逆向学习(五)app进行动态调试 一、写在前面 非常抱歉鸽了那么久,前一段时间一直在忙,现在终于结束了,可以继续更新android逆向系列的,这个系列我会尽力做下去,然后如果可以的话我看看能…...
音频编辑软件Steinberg SpectraLayers Pro mac中文软件介绍
Steinberg SpectraLayers Pro mac是一款专业的音频编辑软件,旨在帮助音频专业人士进行精细的音频编辑和声音处理。它提供了强大的频谱编辑功能,可以对音频文件进行深入的频谱分析和编辑。 Steinberg SpectraLayers Pro mac软件特点 1. 频谱编辑ÿ…...

基于.Net Core实现自定义皮肤WidForm窗口
前言 今天一起来实现基于.Net Core、Windows Form实现自定义窗口皮肤,并实现窗口移动功能。 素材 准备素材:边框、标题栏、关闭按钮图标。 窗体设计 1、创建Window窗体项目 2、窗体设计 拖拉4个Panel控件,分别用于:标题栏、关…...

【Rust】操作日期与时间
目录 介绍 一、计算耗时 二、时间加减法 三、时区转换 四、年月日时分秒 五、时间格式化 介绍 Rust的时间操作主要用到chrono库,接下来我将简单选一些常用的操作进行介绍,如果想了解更多细节,请查看官方文档。 官方文档:chr…...

blender快捷键
1, shift a 添加物体 2,ctrl alt q 切换四格视图 3, ~ 展示物体的各个视图按钮,(~ 就是tab键上面的键) 4,a 全选,全选后,点 ctrl 鼠标框选 减去已经选择的;…...
java Spring Boot 自动启动热部署 (别再改点东西就要重启啦)
上文 java Spring Boot 手动启动热部署 我们实现了一个手动热部署的代码 但其实很多人会觉得 这叫说明热开发呀 这么捞 写完还要手动去点一下 很不友好 其实我们开发人员肯定是希望重启这种事不需要自己手动去做 那么 当然可以 我们就让它自己去做 Build Project 这个操作 我们…...

TouchGFX之后端通信
在大多数应用中,UI需以某种方式连接到系统的其余部分,并发送和接收数据。 它可能会与硬件外设(传感器数据、模数转换和串行通信等)或其他软件模块进行交互通讯。 Model类 所有TouchGFX应用都有Model类,Model类除了存…...

cesium gltf控制
gltf格式详解 glTF格式本质上是一个JSON文件。这一文件描述了整个3D场景的内容。它包含了对场景结构进行描述的场景图。场景中的3D对象通过场景结点引用网格进行定义。材质定义了3D对象的外观,动画定义了3D对象的变换操作(比如选择、平移操作)。蒙皮定义了3D对象如何进行骨骼…...

Spring的依赖注入(DI)以及优缺点
Spring的依赖注入(DI):解释和优点 依赖注入(Dependency Injection,简称DI)是Spring框架的核心概念之一,也是现代Java应用程序开发的重要组成部分。本文将深入探讨DI是什么,以及它的…...

【强化学习】05 —— 基于无模型的强化学习(Prediction)
文章目录 简介蒙特卡洛算法时序差分方法Example1 MC和TD的对比偏差(Bias)/方差(Variance)的权衡Example2 Random WalkExample3 AB 反向传播(backup)Monte-Carlo BackupTemporal-Difference BackupDynamic Programming Backup Boot…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...
