【数据结构】红黑树(C++实现)

📝个人主页:@Sherry的成长之路
🏠学习社区:Sherry的成长之路(个人社区)
📖专栏链接:数据结构
🎯长路漫漫浩浩,万事皆有期待
上一篇博客:【数据结构】AVL树(C++实现)
文章目录
- 红黑树的概念
- 红黑树的性质
- 红黑树结点的定义
- 红黑树的插入
- 红黑树的验证
- 红黑树的查找
- 红黑树的删除
- 红黑树与AVL树的比较
- 总结:
红黑树的概念
红黑树是一种二叉搜索树,但在每个结点上增加了一个存储位用于表示结点的颜色,这个颜色可以是红色的,也可以是黑色的,因此我们称之为红黑树。
红黑树通过对任何一条从根到叶子的路径上各个结点着色方式的限制,确保没有一条路径会比其他路径长出两倍,因此红黑树是近似平衡的。
红黑树的性质
红黑树有以下五点性质:
每个结点不是红色就是黑色。
根结点是黑色的。
如果一个结点是红色的,则它的两个孩子结点是黑色的。
对于每个结点,从该结点到其所有后代叶子结点的简单路径上,均包含相同数目的黑色结点。
每个叶子结点都是黑色的(此处的叶子结点指定是空结点)。
红黑树如何确保从根到叶子的最长可能路径不会超过最短可能路径的两倍?
根据红黑树的性质3可以得出,红黑树当中不会出现连续的红色结点,而根据性质4又可以得出,从某一结点到其后代叶子结点的所有路径上包含的黑色结点的数目是相同的。
我们假设在红黑树中,从根到叶子的所有路径上包含的黑色结点的个数都是N个,那么最短路径就是全部由黑色结点构成的路径,即长度为N。
而最长可能路径就是由一黑一红结点构成的路径,该路径当中黑色结点与红色结点的数目相同,即长度为2N。
因此,红黑树从根到叶子的最长可能路径不会超过最短可能路径的两倍。
红黑树结点的定义
我们这里直接实现KV模型的红黑树,为了方便后序的旋转操作,将红黑树的结点定义为三叉链结构,除此之外还新加入了一个成员变量,用于表示结点的颜色。
template<class K, class V>
struct RBTreeNode
{//三叉链RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;//存储的键值对pair<K, V> _kv;//结点的颜色int _col; //红/黑//构造函数RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};
在这里我们可以使用枚举来定义结点的颜色,这样可以增加代码的可读性和可维护性,并且便于后序的调试操作。
//枚举定义结点的颜色
enum Colour
{RED,BLACK
};
为什么构造结点时,默认将结点的颜色设置为红色?
当我们向红黑树插入结点时,若我们插入的是黑色结点,那么插入路径上黑色结点的数目就比其他路径上黑色结点的数目多了一个,即破坏了红黑树的性质4,此时我们就需要对红黑树进行调整。
若我们插入红黑树的结点是红色的,此时如果其父结点也是红色的,那么表明出现了连续的红色结点,即破坏了红黑树的性质3,此时我们需要对红黑树进行调整;但如果其父结点是黑色的,那我们就无需对红黑树进行调整,插入后仍满足红黑树的要求。
总结一下:
插入黑色结点,一定破坏红黑树的性质4,必须对红黑树进行调整。
插入红色结点,可能破坏红黑树的性质3,可能对红黑树进行调整。
权衡利弊后,我们在构造结点进行插入时,默认将结点的颜色设置为红色。
红黑树的插入
红黑树插入结点的逻辑分为三步:
按二叉搜索树的插入方法,找到待插入位置。
将待插入结点插入到树中。
若插入结点的父结点是红色的,则需要对红黑树进行调整。
其中前两步与二叉搜索树插入结点时的逻辑相同,红黑树的关键在于第三步对红黑树的调整。
红黑树在插入结点后是如何调整的?
实际上,在插入结点后并不是一定会对红黑树进行调整,若插入结点的父结点是黑色的,那么我们就不用对红黑树进行调整,因为本次结点的插入并没有破坏红黑树的五点性质。
只有当插入结点的父结点是红色时才需要对红黑树进行调整,因为我们默认插入的结点就是红色的,如果插入结点的父结点也是红色的,那么此时就出现了连续的红色结点,因此需要对红黑树进行调整。
因为插入结点的父结点是红色的,说明父结点不是根结点(根结点是黑色的),因此插入结点的祖父结点(父结点的父结点)就一定存在。
红黑树调整时具体应该如何调整,主要是看插入结点的叔叔(插入结点的父结点的兄弟结点),根据插入结点叔叔的不同,可将红黑树的调整分为三种情况。
情况一:插入结点的叔叔存在,且叔叔的颜色是红色。
此时为了避免出现连续的红色结点,我们可以将父结点变黑,但为了保持每条路径黑色结点的数目不变,因此我们还需要将祖父结点变红,再将叔叔变黑。这样一来既保持了每条路径黑色结点的数目不变,也解决了连续红色结点的问题。
但调整还没有结束,因为此时祖父结点变成了红色,如果祖父结点是根结点,那我们直接再将祖父结点变成黑色即可,此时相当于每条路径黑色结点的数目都增加了一个。
但如果祖父结点不是根结点的话,我们就需要将祖父结点当作新插入的结点,再判断其父结点是否为红色,若其父结点也是红色,那么又需要根据其叔叔的不同,进而进行不同的调整操作。
因此,情况一的抽象图表示如下:
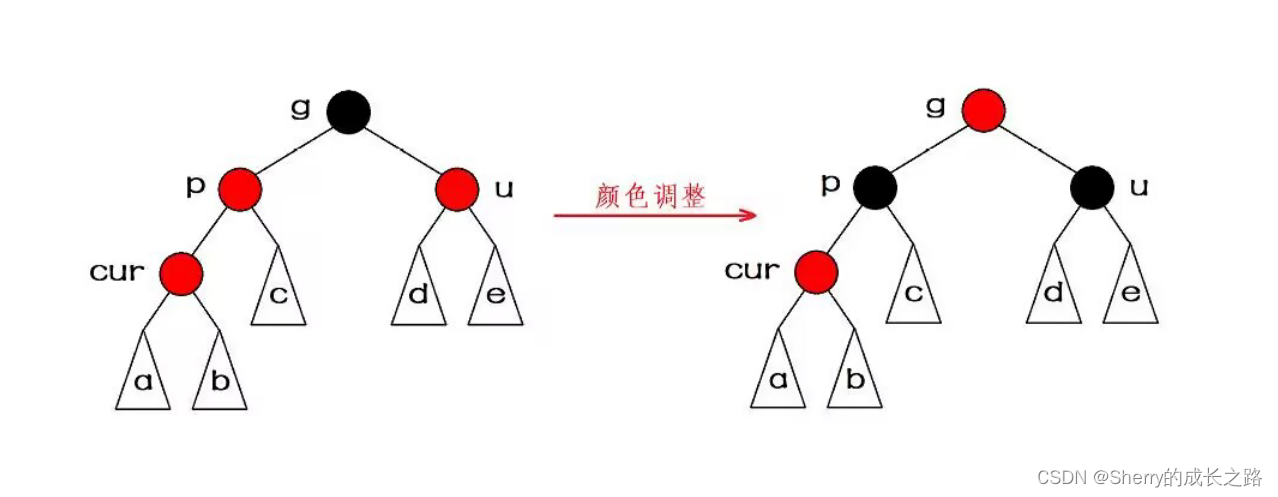
注意: 叔叔存在且为红时,cur结点是parent的左孩子还是右孩子,调整方法都是一样的。
情况二:插入结点的叔叔存在,且叔叔的颜色是黑色。
这种情况一定是在情况一继续往上调整的过程中出现的,即这种情况下的cur结点一定不是新插入的结点,而是上一次情况一调整过程中的祖父结点,如下图:
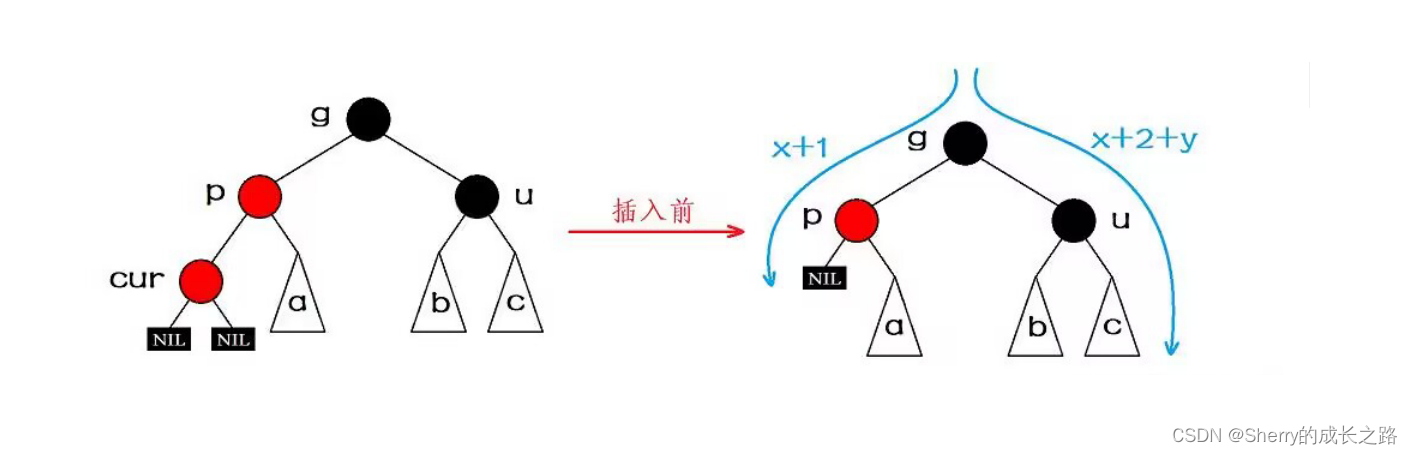
我们将路径中祖父结点之上黑色结点的数目设为x xx,将叔叔结点之下黑色结点的数目设为y yy,则在插入结点前,图示两条路径黑色结点的数目分别为x+1 和x+2+y,很明显x+2+y 是一定大于 x+1的,因此在插入结点前就不满足红黑树的要求了,所以说叔叔结点存在且为黑这种情况,一定是由情况一往上调整过程中才会出现的一种情况。
需要注意:
从根结点一直走到空位置就算一条路径,而不是从根结点走到左右结点均为空的叶子结点时才算一条路径。
情况二和情况三均需要进行旋转处理,旋转处理后无需继续往上进行调整,所以说情况二一定是由情况一往上调整的过程中出现的。
出现叔叔存在且为黑时,单纯使用变色已经无法处理了,这时我们需要进行旋转处理。若祖孙三代的关系是直线(cur、parent、grandfather这三个结点为一条直线),则我们需要先进行单旋操作,再进行颜色调整,颜色调整后这棵被旋转子树的根结点是黑色的,因此无需继续往上进行处理。
抽象图表示如下:
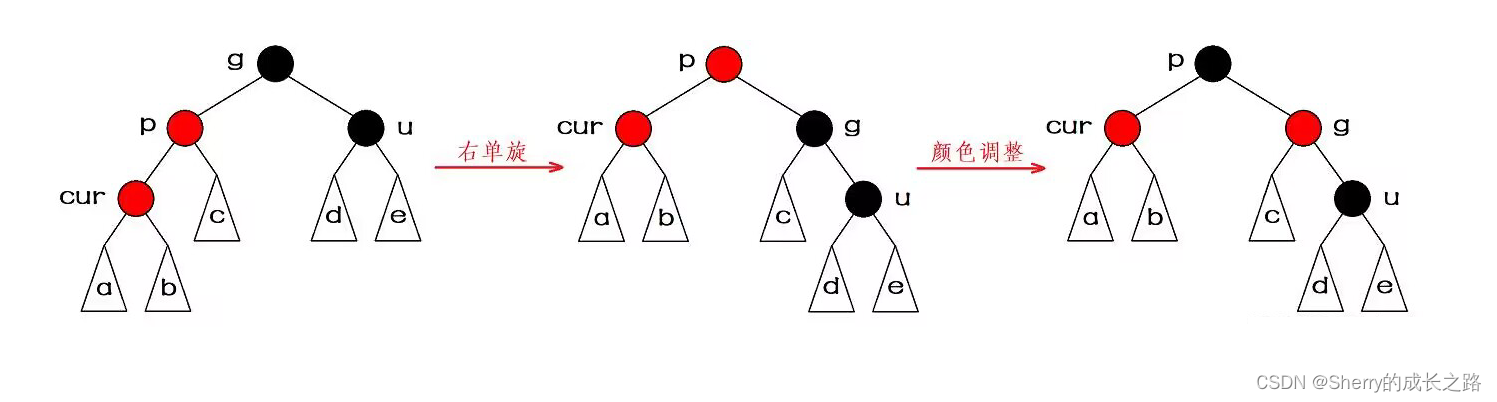
说明一下: 当直线关系为,parent是grandfather的右孩子,cur是parent的右孩子时,就需要先进行左单旋操作,再进行颜色调整。
若祖孙三代的关系是折现(cur、parent、grandfather这三个结点为一条折现),则我们需要先进行双旋操作,再进行颜色调整,颜色调整后这棵被旋转子树的根是黑色的,因此无需继续往上进行处理。
抽象图表示如下:
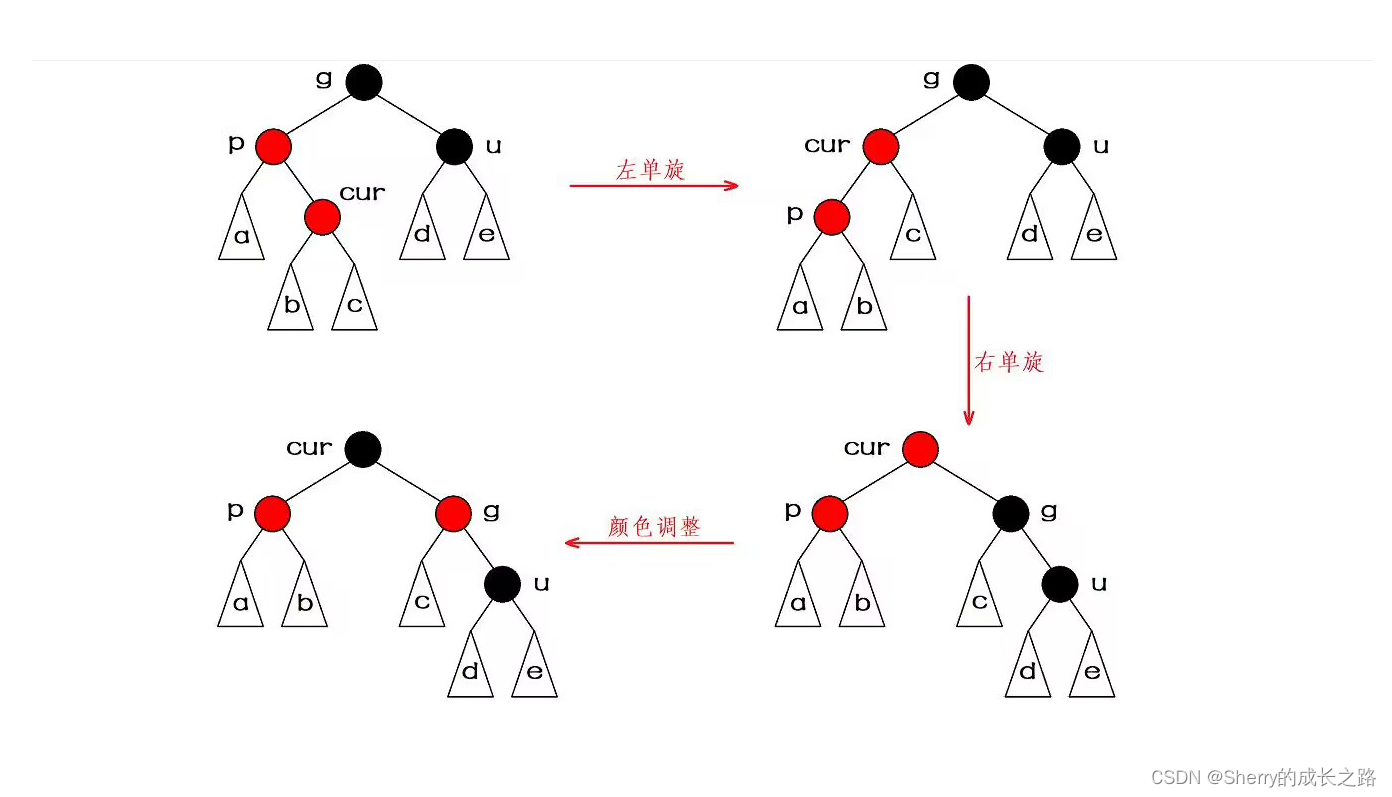
说明一下: 当折现关系为,parent是grandfather的右孩子,cur是parent的左孩子时,就需要先进行右左双旋操作,再进行颜色调整。
情况三:插入结点的叔叔不存在。
在这种情况下的cur结点一定是新插入的结点,而不可能是由情况一变化而来的,因为叔叔不存在说明在parent的下面不可能再挂黑色结点了,如下图:
如果插入前parent下面再挂黑色结点,就会导致图中两条路径黑色结点的数目不相同,而parent是红色的,因此parent下面自然也不能挂红色结点,所以说这种情况下的cur结点一定是新插入的结点。
和情况二一样,若祖孙三代的关系是直线(cur、parent、grandfather这三个结点为一条直线),则我们需要先进行单旋操作,再进行颜色调整,颜色调整后这棵被旋转子树的根结点是黑色的,因此无需继续往上进行处理。
抽象图表示如下:
说明一下: 当直线关系为,parent是grandfather的右孩子,cur是parent的右孩子时,就需要先进行左单旋操作,再进行颜色调整。
若祖孙三代的关系是折现(cur、parent、grandfather这三个结点为一条折现),则我们需要先进行双旋操作,再进行颜色调整,颜色调整后这棵被旋转子树的根是黑色的,因此无需继续往上进行处理。
抽象图表示如下:
说明一下: 当折现关系为,parent是grandfather的右孩子,cur是parent的左孩子时,就需要先进行右左双旋操作,再进行颜色调整。
代码如下:
//插入函数
pair<Node*, bool> Insert(const pair<K, V>& kv)
{if (_root == nullptr) //若红黑树为空树,则插入结点直接作为根结点{_root = new Node(kv);_root->_col = BLACK; //根结点必须是黑色return make_pair(_root, true); //插入成功}//1、按二叉搜索树的插入方法,找到待插入位置Node* cur = _root;Node* parent = nullptr;while (cur){if (kv.first < cur->_kv.first) //待插入结点的key值小于当前结点的key值{//往该结点的左子树走parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first) //待插入结点的key值大于当前结点的key值{//往该结点的右子树走parent = cur;cur = cur->_right;}else //待插入结点的key值等于当前结点的key值{return make_pair(cur, false); //插入失败}}//2、将待插入结点插入到树中cur = new Node(kv); //根据所给值构造一个结点Node* newnode = cur; //记录新插入的结点(便于后序返回)if (kv.first < parent->_kv.first) //新结点的key值小于parent的key值{//插入到parent的左边parent->_left = cur;cur->_parent = parent;}else //新结点的key值大于parent的key值{//插入到parent的右边parent->_right = cur;cur->_parent = parent;}//3、若插入结点的父结点是红色的,则需要对红黑树进行调整while (parent&&parent->_col == RED){Node* grandfather = parent->_parent; //parent是红色,则其父结点一定存在if (parent == grandfather->_left) //parent是grandfather的左孩子{Node* uncle = grandfather->_right; //uncle是grandfather的右孩子if (uncle&&uncle->_col == RED) //情况1:uncle存在且为红{//颜色调整parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续往上处理cur = grandfather;parent = cur->_parent;}else //情况2+情况3:uncle不存在 + uncle存在且为黑{if (cur == parent->_left){RotateR(grandfather); //右单旋//颜色调整grandfather->_col = RED;parent->_col = BLACK;}else //cur == parent->_right{RotateLR(grandfather); //左右双旋//颜色调整grandfather->_col = RED;cur->_col = BLACK;}break; //子树旋转后,该子树的根变成了黑色,无需继续往上进行处理}}else //parent是grandfather的右孩子{Node* uncle = grandfather->_left; //uncle是grandfather的左孩子if (uncle&&uncle->_col == RED) //情况1:uncle存在且为红{//颜色调整uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//继续往上处理cur = grandfather;parent = cur->_parent;}else //情况2+情况3:uncle不存在 + uncle存在且为黑{if (cur == parent->_left){RotateRL(grandfather); //右左双旋//颜色调整cur->_col = BLACK;grandfather->_col = RED;}else //cur == parent->_right{RotateL(grandfather); //左单旋//颜色调整grandfather->_col = RED;parent->_col = BLACK;}break; //子树旋转后,该子树的根变成了黑色,无需继续往上进行处理}}}_root->_col = BLACK; //根结点的颜色为黑色(可能被情况一变成了红色,需要变回黑色)return make_pair(newnode, true); //插入成功
}//左单旋
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;Node* parentParent = parent->_parent;//建立subRL与parent之间的联系parent->_right = subRL;if (subRL)subRL->_parent = parent;//建立parent与subR之间的联系subR->_left = parent;parent->_parent = subR;//建立subR与parentParent之间的联系if (parentParent == nullptr){_root = subR;_root->_parent = nullptr;}else{if (parent == parentParent->_left){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}
}//右单旋
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;Node* parentParent = parent->_parent;//建立subLR与parent之间的联系parent->_left = subLR;if (subLR)subLR->_parent = parent;//建立parent与subL之间的联系subL->_right = parent;parent->_parent = subL;//建立subL与parentParent之间的联系if (parentParent == nullptr){_root = subL;_root->_parent = nullptr;}else{if (parent == parentParent->_left){parentParent->_left = subL;}else{parentParent->_right = subL;}subL->_parent = parentParent;}
}//左右双旋
void RotateLR(Node* parent)
{RotateL(parent->_left);RotateR(parent);
}//右左双旋
void RotateRL(Node* parent)
{RotateR(parent->_right);RotateL(parent);
}
注意: 在红黑树调整后,需要将根结点的颜色变为黑色,因为红黑树的根结点可能在情况一的调整过程中被变成了红色。
红黑树的验证
红黑树也是一种特殊的二叉搜索树,因此我们可以先获取二叉树的中序遍历序列,来判断该二叉树是否满足二叉搜索树的性质。
代码如下:
//中序遍历
void Inorder()
{_Inorder(_root);
}
//中序遍历子函数
void _Inorder(Node* root)
{if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << " ";_Inorder(root->_right);
}
但中序有序只能证明是二叉搜索树,要证明二叉树是红黑树还需验证该二叉树是否满足红黑树的性质。
代码如下:
//判断是否为红黑树
bool ISRBTree()
{if (_root == nullptr) //空树是红黑树{return true;}if (_root->_col == RED){cout << "error:根结点为红色" << endl;return false;}//找最左路径作为黑色结点数目的参考值Node* cur = _root;int BlackCount = 0;while (cur){if (cur->_col == BLACK)BlackCount++;cur = cur->_left;}int count = 0;return _ISRBTree(_root, count, BlackCount);
}
//判断是否为红黑树的子函数
bool _ISRBTree(Node* root, int count, int BlackCount)
{if (root == nullptr) //该路径已经走完了{if (count != BlackCount){cout << "error:黑色结点的数目不相等" << endl;return false;}return true;}if (root->_col == RED&&root->_parent->_col == RED){cout << "error:存在连续的红色结点" << endl;return false;}if (root->_col == BLACK){count++;}return _ISRBTree(root->_left, count, BlackCount) && _ISRBTree(root->_right, count, BlackCount);
}
红黑树的查找
红黑树的查找函数与二叉搜索树的查找方式一模一样,逻辑如下:
若树为空树,则查找失败,返回nullptr。
若key值小于当前结点的值,则应该在该结点的左子树当中进行查找。
若key值大于当前结点的值,则应该在该结点的右子树当中进行查找。
若key值等于当前结点的值,则查找成功,返回对应结点。
代码如下:
//查找函数
Node* Find(const K& key)
{Node* cur = _root;while (cur){if (key < cur->_kv.first) //key值小于该结点的值{cur = cur->_left; //在该结点的左子树当中查找}else if (key > cur->_kv.first) //key值大于该结点的值{cur = cur->_right; //在该结点的右子树当中查找}else //找到了目标结点{return cur; //返回该结点}}return nullptr; //查找失败
}红黑树的删除
红黑树的删除要比插入更加难以理解,但是只要仔细一点也还行。
第一步:找到实际待删除的结点
找结点的过程与二叉搜索树寻找待删除结点的方法一样,若找到的待删除结点的左右子树均不为空,则需要使用替换法进行删除。因此我们最终需要删除的都是左右子树至少有一个为空的结点。
找到实际待删除结点后,先不删除该结点,否则调整红黑树时不容易控制,找到实际待删除结点后立即进行红黑树的调整。
第二步:调整红黑树
调整红黑树之前,我们先判断一下本次结点的删除是否会破坏了红黑树的性质,若破坏了我们才需要对红黑树进行调整。
若实际删除的结点是红色结点,那么本次删除操作不会破坏红黑树的性质,因此我们不需要对红黑树进行调整。反之,若删除的结点是黑色结点,我们就需要对红黑树进行调整,因为黑色结点的删除将会使得一些路径中黑色结点的数目减少,此时便破坏了红黑树的性质四。
我们先来说最简单的一种情况,即待删除结点只有一个孩子为空的情况。
在这种情况下,待删除结点要么是只有左孩子,要么是有只右孩子,但不管是左孩子还是右孩子,这个孩子一定是红色的,因为若这个孩子是黑色的,那么此时图示长蓝色路径的黑色结点数目比短蓝色路径的黑色结点数目多,不符合红黑树的性质。
又因为红黑树当中不允许出现连续的红色结点,因此在这种情况下实际上就只有图示两种实际情况,这时我们直接将待删除结点的那个红孩子变成黑色就行了,因为在后面实际删除结点时会将这个孩子连接到删除结点的父结点下面,连接后相当于我们删除的是一个红色结点,红黑树调整完成。
下面再来说比较复杂的情况,即待删除结点的左右孩子均为空。
我们以待删除结点是其父结点的左孩子为例,分为以下四种情况:
图示说明:
若parent结点为白色,表明parent结点可能是红色结点也可能是黑色结点。
若bL或bR结点为白色,表明其可能是红色结点或黑色结点甚至该结点不存在。
bL和bR结点为黑色时,表明他们可能是黑色结点或该结点不存在。
情况一:brother为红色。
当待删除结点的brother为红色时,我们先以parent为旋转点进行一次左单旋,再将brother的颜色变为黑色,将parent的颜色变为红色,此时我们再对待删除结点cur进行情况分析,情况一就转换成了情况二、三或四。
情况二:brother为黑色,且其左右孩子都是黑色结点或为空。
在该情况下,我们直接将brother的颜色变成红色,此时根据parent的颜色决定红黑树的调整是否结束,若parent的颜色是红色,则我们将parent变为黑色后即可结束红黑树的调整;若parent的颜色原本就是黑色,则我们需要将parent结点当作下一次调整时的cur结点进行情况分析,并且情况二在下一次调整时可能会是情况一、二、三、四当中的任何一种。
情况三:brother为黑色,且其左孩子是红色结点,右孩子是黑色结点或为空。
出现该情况时,我们先以brother为旋转点进行一次右单旋,再将brother结点变为红色,将brotherLeft变为黑色,此时我们再对待删除结点cur进行情况分析,情况三就转换成了情况四。
情况四:brother为黑色,且其右孩子是红色结点。
经过情况四的处理后,红黑树就一定调整结束了。在情况四当中,我们先以parent为旋转点进行一次左单旋,然后将parent的颜色赋值给brother,再将parent的颜色变为黑色,最后将brotherRight变为黑色,此时红黑树的调整便结束了。
说明一下:
待删除结点是其父结点的右孩子时的四种情况与上面四种情况类似,这里就不列举出来了。
若待删除结点没有父结点,即待删除结点是根结点时,在找到该结点时就进行了删除,这里不用考虑,具体看代码。
这里有必要对各种情况的切换进行说明,你可能会担心调整红黑树时在这四种情况当中一直来回切换而不能跳出,下面我们来对此进行分析:
首先,进入情况四后红黑树就一定调整结束了。其次,进入情况三后,下次也一定会进入情况四,红黑树的调整也会结束。所以情况三和情况四是没有问题的,你们最纠结的只能是情况一和情况二了。
情况一又会切换为情况二、三、四,因此只要情况二能够有办法退出,那么所有情况就都能退出了。
在情况二当中我们说,如果parent的颜色是红色,那么我们将parent变为黑色后就可以结束红黑树的调整,那会不会每次进入情况二时parent的颜色都不是红色,而一直是黑色的呢?
当然有可能,但是我们若一直往上进行调整时,那么总会调整到红黑树的根结点,当调整到根结点后我们便不用进行调整了,此时根结点虽然是黑色的,但是不影响,这仅仅意味着每条从根到叶子的路径上包含的黑色结点的个数都减少了一个,此时也没有破坏红黑树的性质,也就完成了红黑树的调整,因此在调整过程中不会出现一直在这四种情况来回切换而不能跳出的问题。
第三步:进行结点的实际删除
在红黑树调整完毕后,我们就可以进行结点的删除了,删除结点的方式很简单,若待删除结点有左孩子或右孩子,我们将其左孩子或右孩子连接到待删除结点父结点的下面即可,之后便可以将待删除结点删除了。
代码如下:
//删除函数
bool Erase(const K& key)
{//用于遍历二叉树Node* parent = nullptr;Node* cur = _root;//用于标记实际的待删除结点及其父结点Node* delParentPos = nullptr;Node* delPos = nullptr;while (cur){if (key < cur->_kv.first) //所给key值小于当前结点的key值{//往该结点的左子树走parent = cur;cur = cur->_left;}else if (key > cur->_kv.first) //所给key值大于当前结点的key值{//往该结点的右子树走parent = cur;cur = cur->_right;}else //找到了待删除结点{if (cur->_left == nullptr) //待删除结点的左子树为空{if (cur == _root) //待删除结点是根结点{_root = _root->_right; //让根结点的右子树作为新的根结点if (_root){_root->_parent = nullptr;_root->_col = BLACK; //根结点为黑色}delete cur; //删除原根结点return true;}else{delParentPos = parent; //标记实际删除结点的父结点delPos = cur; //标记实际删除的结点}break; //进行红黑树的调整以及结点的实际删除}else if (cur->_right == nullptr) //待删除结点的右子树为空{if (cur == _root) //待删除结点是根结点{_root = _root->_left; //让根结点的左子树作为新的根结点if (_root){_root->_parent = nullptr;_root->_col = BLACK; //根结点为黑色}delete cur; //删除原根结点return true;}else{delParentPos = parent; //标记实际删除结点的父结点delPos = cur; //标记实际删除的结点}break; //进行红黑树的调整以及结点的实际删除}else //待删除结点的左右子树均不为空{//替换法删除//寻找待删除结点右子树当中key值最小的结点作为实际删除结点Node* minParent = cur;Node* minRight = cur->_right;while (minRight->_left){minParent = minRight;minRight = minRight->_left;}cur->_kv.first = minRight->_kv.first; //将待删除结点的key改为minRight的keycur->_kv.second = minRight->_kv.second; //将待删除结点的value改为minRight的valuedelParentPos = minParent; //标记实际删除结点的父结点delPos = minRight; //标记实际删除的结点break; //进行红黑树的调整以及结点的实际删除}}}if (delPos == nullptr) //delPos没有被修改过,说明没有找到待删除结点{return false;}//记录待删除结点及其父结点(用于后续实际删除)Node* del = delPos;Node* delP = delParentPos;//调整红黑树if (delPos->_col == BLACK) //删除的是黑色结点{if (delPos->_left) //待删除结点有一个红色的左孩子(不可能是黑色){delPos->_left->_col = BLACK; //将这个红色的左孩子变黑即可}else if (delPos->_right) //待删除结点有一个红色的右孩子(不可能是黑色){delPos->_right->_col = BLACK; //将这个红色的右孩子变黑即可}else //待删除结点的左右均为空{while (delPos != _root) //可能一直调整到根结点{if (delPos == delParentPos->_left) //待删除结点是其父结点的左孩子{Node* brother = delParentPos->_right; //兄弟结点是其父结点的右孩子//情况一:brother为红色if (brother->_col == RED){delParentPos->_col = RED;brother->_col = BLACK;RotateL(delParentPos);//需要继续处理brother = delParentPos->_right; //更新brother(否则在本循环中执行其他情况的代码会出错)}//情况二:brother为黑色,且其左右孩子都是黑色结点或为空if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK))){brother->_col = RED;if (delParentPos->_col == RED){delParentPos->_col = BLACK;break;}//需要继续处理delPos = delParentPos;delParentPos = delPos->_parent;}else{//情况三:brother为黑色,且其左孩子是红色结点,右孩子是黑色结点或为空if ((brother->_right == nullptr) || (brother->_right->_col == BLACK)){brother->_left->_col = BLACK;brother->_col = RED;RotateR(brother);//需要继续处理brother = delParentPos->_right; //更新brother(否则执行下面情况四的代码会出错)}//情况四:brother为黑色,且其右孩子是红色结点brother->_col = delParentPos->_col;delParentPos->_col = BLACK;brother->_right->_col = BLACK;RotateL(delParentPos);break; //情况四执行完毕后调整一定结束}}else //delPos == delParentPos->_right //待删除结点是其父结点的左孩子{Node* brother = delParentPos->_left; //兄弟结点是其父结点的左孩子//情况一:brother为红色if (brother->_col == RED) //brother为红色{delParentPos->_col = RED;brother->_col = BLACK;RotateR(delParentPos);//需要继续处理brother = delParentPos->_left; //更新brother(否则在本循环中执行其他情况的代码会出错)}//情况二:brother为黑色,且其左右孩子都是黑色结点或为空if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK))){brother->_col = RED;if (delParentPos->_col == RED){delParentPos->_col = BLACK;break;}//需要继续处理delPos = delParentPos;delParentPos = delPos->_parent;}else{//情况三:brother为黑色,且其右孩子是红色结点,左孩子是黑色结点或为空if ((brother->_left == nullptr) || (brother->_left->_col == BLACK)){brother->_right->_col = BLACK;brother->_col = RED;RotateL(brother);//需要继续处理brother = delParentPos->_left; //更新brother(否则执行下面情况四的代码会出错)}//情况四:brother为黑色,且其左孩子是红色结点brother->_col = delParentPos->_col;delParentPos->_col = BLACK;brother->_left->_col = BLACK;RotateR(delParentPos);break; //情况四执行完毕后调整一定结束}}}}}//进行实际删除if (del->_left == nullptr) //实际删除结点的左子树为空{if (del == delP->_left) //实际删除结点是其父结点的左孩子{delP->_left = del->_right;if (del->_right)del->_right->_parent = delP;}else //实际删除结点是其父结点的右孩子{delP->_right = del->_right;if (del->_right)del->_right->_parent = delP;}}else //实际删除结点的右子树为空{if (del == delP->_left) //实际删除结点是其父结点的左孩子{delP->_left = del->_left;if (del->_left)del->_left->_parent = delP;}else //实际删除结点是其父结点的右孩子{delP->_right = del->_left;if (del->_left)del->_left->_parent = delP;}}delete del; //实际删除结点return true;
}
红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删查改的时间复杂度都是O(logN),但红黑树和AVL树控制二叉树平衡的方式不同:
AVL树是通过控制左右高度差不超过1来实现二叉树平衡的,实现的是二叉树的严格平衡。
红黑树是通过控制结点的颜色,从而使得红黑树当中最长可能路径不超过最短可能路径的2倍,实现的是近似平衡。
相对于AVL树来说,红黑树降低了插入结点时需要进行的旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,实际运用时也大多用的是红黑树。
总结:
今天我们比较详细地完成了红黑树的C++实现,了解了一些有关的底层原理。接下来,我们将进行STL中 set、map、multiset、multimap类的学习。希望我的文章和讲解能对大家的学习提供一些帮助。
当然,本文仍有许多不足之处,欢迎各位小伙伴们随时私信交流、批评指正!我们下期见~

相关文章:

【数据结构】红黑树(C++实现)
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 上一篇博客:【数据…...
图论 part 03)
day-64 代码随想录算法训练营(19)图论 part 03
827.最大人工岛 思路一:深度优先遍历 1.深度优先遍历,求出所有岛屿的面积,并且把每个岛屿记上不同标记2.使用 unordered_map 使用键值对,标记:面积,记录岛屿面积3.遍历所有海面,然后进行一次广…...

xss测试步骤总结
文章目录 测试流程1.开启burp2.测试常规xss语句3.观察回显4.测试闭合与绕过Level2Level3Level4Level5Level6Level7 5.xss绕过方法1)测试需观察点2)无过滤法3)">闭合4)单引号闭合事件函数5)双引号闭合事件函数6)引号闭合链接7)大小写绕过8)多写绕过9)unicode编码10)unic…...
2023最新简易ChatGPT3.5小程序全开源源码+全新UI首发+实测可用可二开(带部署教程)
源码简介: 2023最新简易ChatGPT3.5小程序全开源源码全新UI首发,实测可以用,而且可以二次开发。这个是最新ChatGPT智能AI机器人微信小程序源码,同时也带部署教程。 这个全新版本的小界面设计相当漂亮,简单大方&#x…...
【Redis】数据过期策略和数据淘汰策略
数据过期策略和淘汰策略 过期策略 Redis所有的数据结构都可以设置过期时间,时间一到,就会自动删除。 问题:大家都知道,Redis是单线程的,如果同一时间太多key过期,Redis删除的时间也会占用线程的处理时间…...

RPA的优势和劣势是什么,RPA能力边界在哪里?
RPA,即Robotic Process Automation(机器人流程自动化),是一种新型的自动化技术,它可以通过软件机器人模拟人类在计算机上执行的操作,从而实现业务流程的自动化。RPA技术的出现,为企业提高效率、…...
Kubernetes 学习总结(38)—— Kubernetes 与云原生的联系
一、什么是云原生? 伴随着云计算的浪潮,云原生概念也应运而生,而且火得一塌糊涂,大家经常说云原生,却很少有人告诉你到底什么是云原生,云原生可以理解为“云”“原生”,Cloud 可以理解为应用程…...
号卡推广管理系统源码/手机流量卡推广网站源码/PHP源码+带后台版本+分销系统
源码简介: 号卡推广管理系统源码/手机流量卡推广网站源码,基于PHP源码,而且它是带后台版本,分销系统。运用全新UI流量卡官网系统源码有后台带文章。 这个流量卡销售网站源码,PHP流量卡分销系统,它可以支持…...
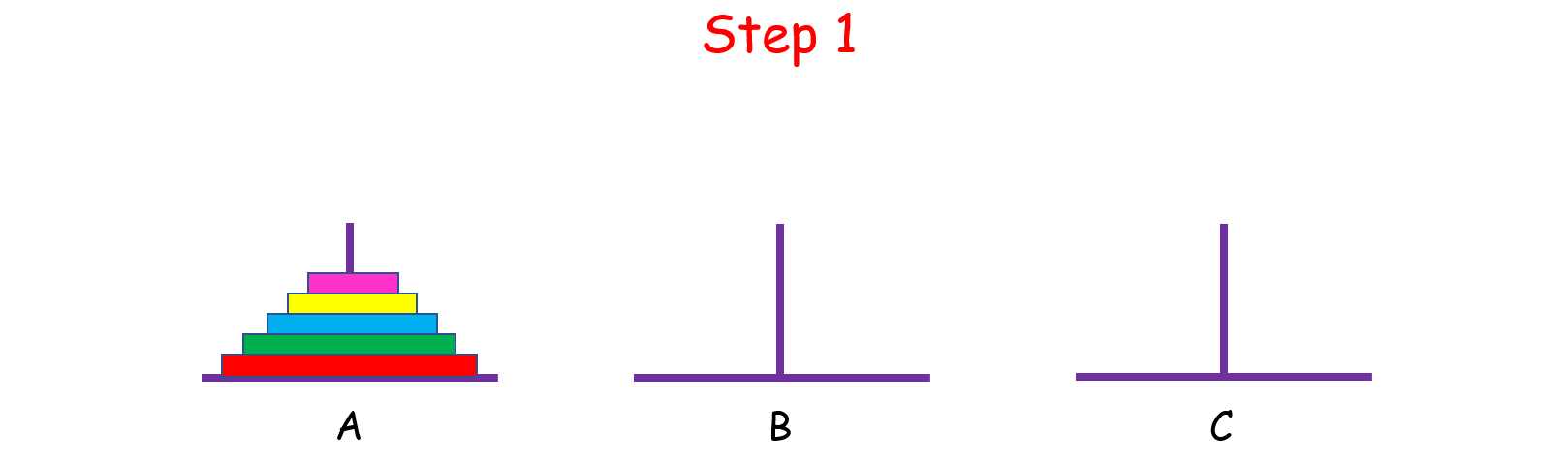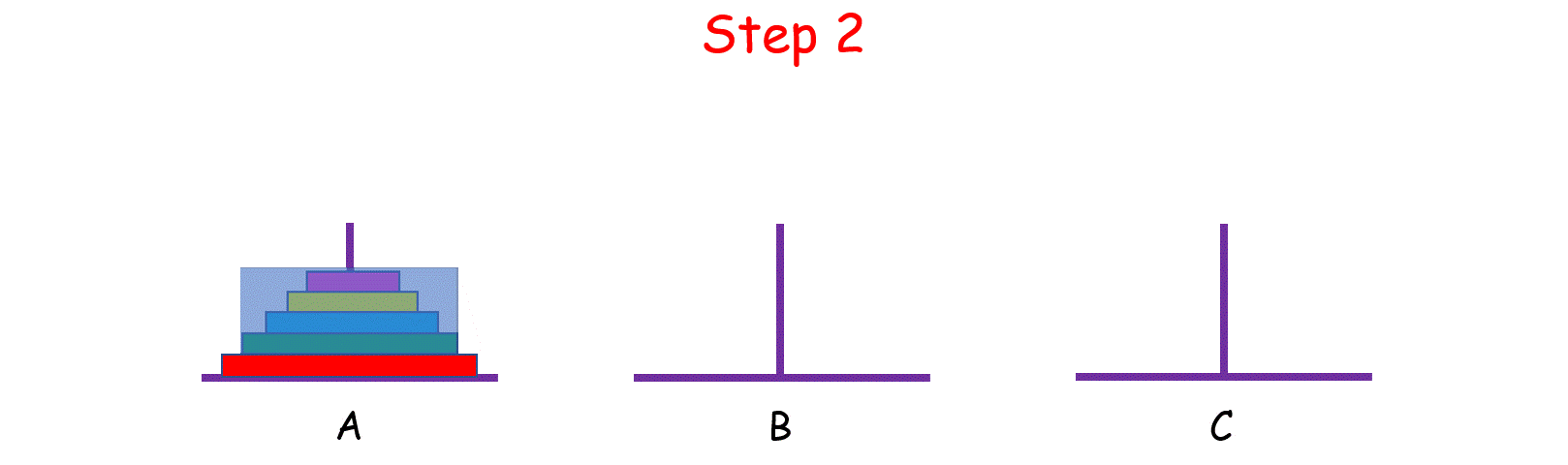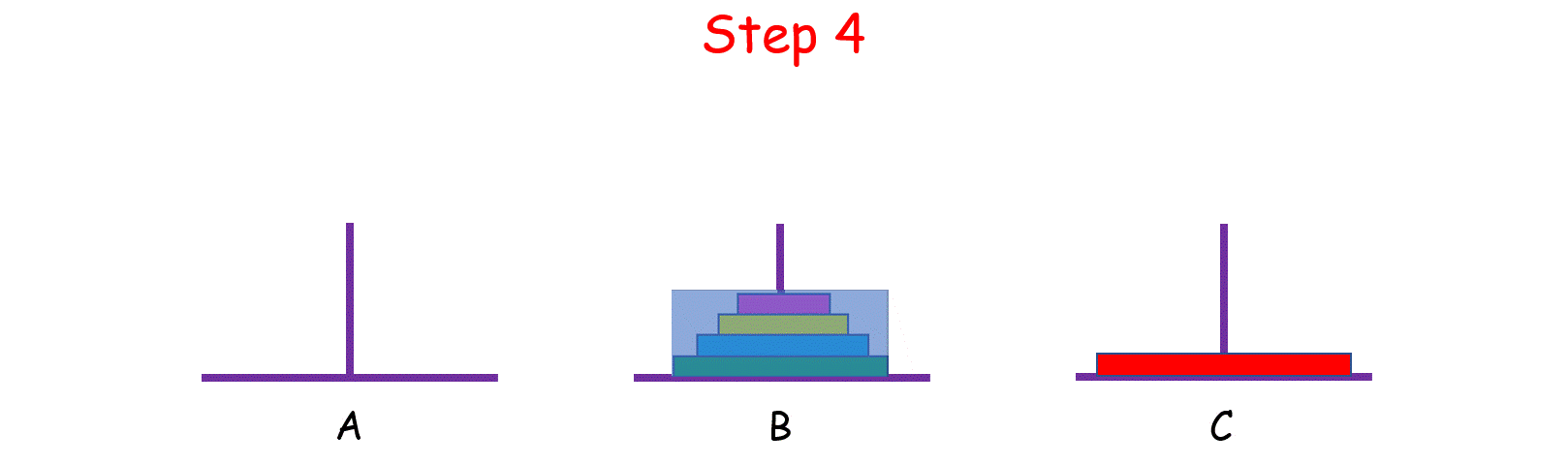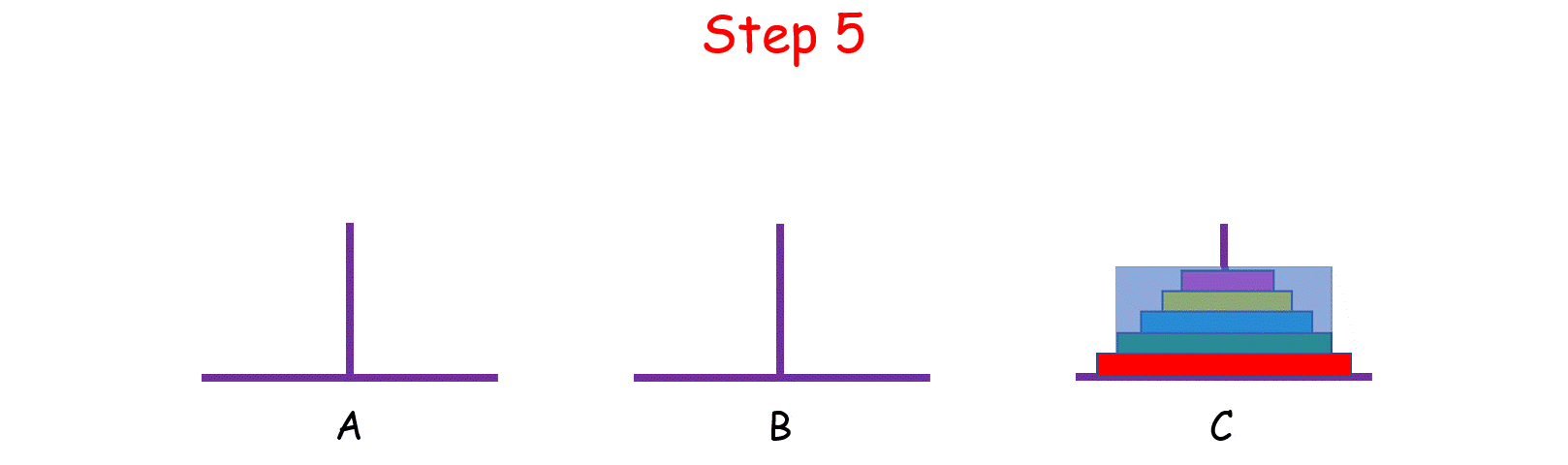
【C语言】汉诺塔 —— 详解
一、介绍 汉诺塔(Tower of Hanoi),又称河内塔,是一个源于印度古老传说的益智玩具。大焚天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。 大焚天命令婆罗门把圆盘从下面开始按…...
【云备份】
文章目录 [toc] 1 :peach:云备份的认识:peach:1.1 :apple:功能了解:apple:1.2 :apple:实现目标:apple:1.3 :apple:服务端程序负责功能:apple:1.4 :apple:服务端功能模块划分:apple:1.5 :apple:客户端程序负责功能:apple:1.6 :apple:客户端功能模块划分:apple: 2 :peach:环境搭建…...

第四十六章 命名空间和数据库 - 系统提供的数据库
文章目录 第四十六章 命名空间和数据库 - 系统提供的数据库系统提供的数据库ENSLIBIRISAUDITIRISLIBIRISLOCALDATAIRISSYS (the system manager’s database 系统管理器的数据库)IRISTEMP 第四十六章 命名空间和数据库 - 系统提供的数据库 系统提供的数据库 IRIS 提供以下数据…...

【贪心的商人】python实现-附ChatGPT解析
1.题目 贪心的商人 知识点:贪心 时间限制:1s 空间限制: 256MB 限定语言:不限 题目描述: 商人经营一家店铺,有number种商品,由于仓库限制 每件商品的最大持有数量是item[index], 每种商品的价格在每天是item_price[item_index][day], 通过对商品的买进和卖出获取利润,请给…...
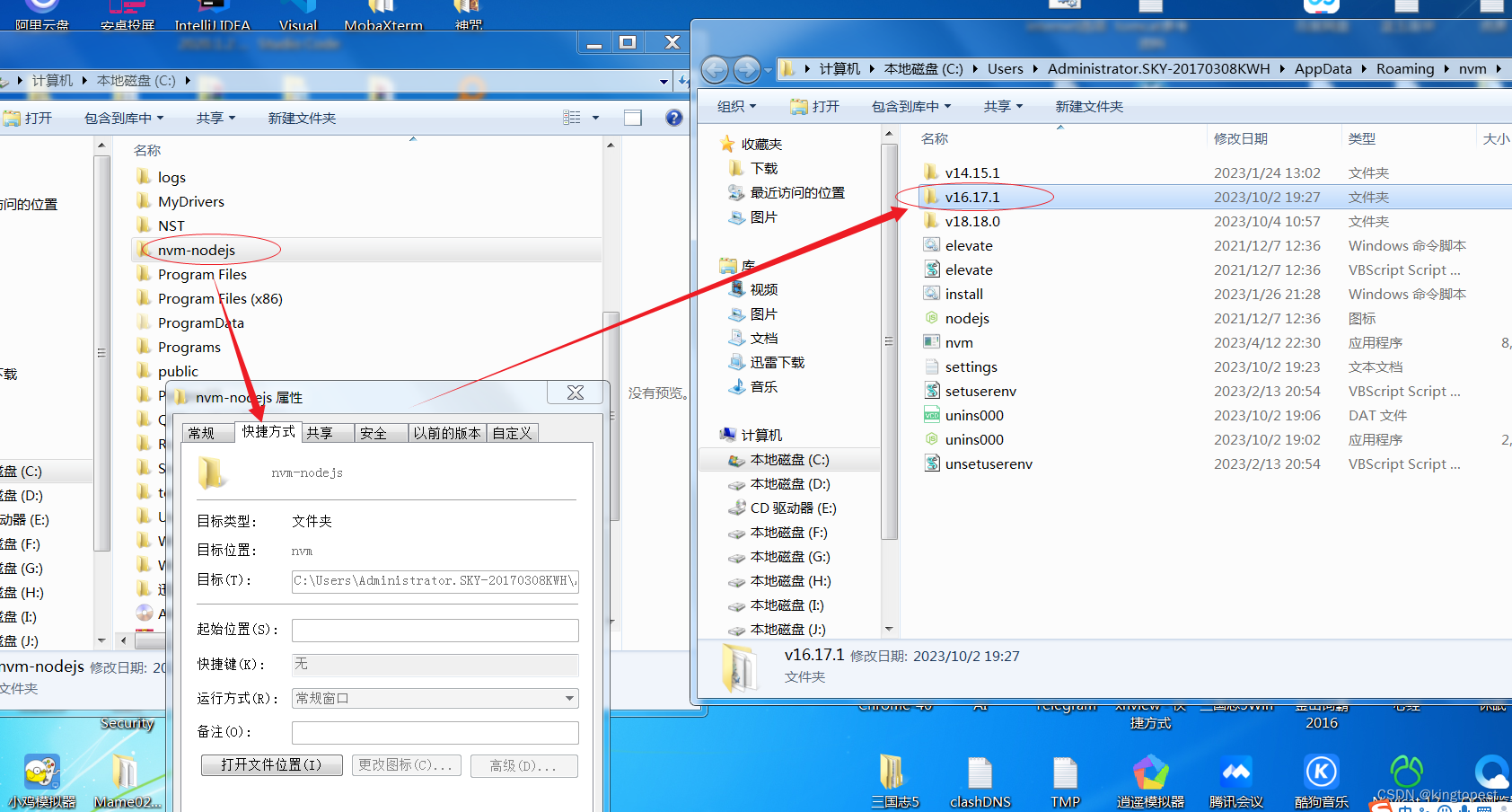
解决nvm切换node版本失败的终极办法-秒杀网上99%的水文
nvm是一款强大的node多版本管理器,可以轻易选择你需要的node版本,这对win7平台简直就是超好的福音:可以突破node 14.15以上的安装限制。 但是nvm安装有一个巨大的坑点:nvm use 版本号以后,并没有生效,nvm …...
2023蓝帽杯半决赛电子取证+CTF部分题解
文章目录 电子取证123456789101112131415 CTFWeb | MyLinuxBotWeb | AirticleShareCrypto | ezrsaPwn | AdminPwn | uafmisc|排排坐吃吃果果 电子取证 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 CTF Web | MyLinuxBot Web | AirticleShare import requests import times reques…...
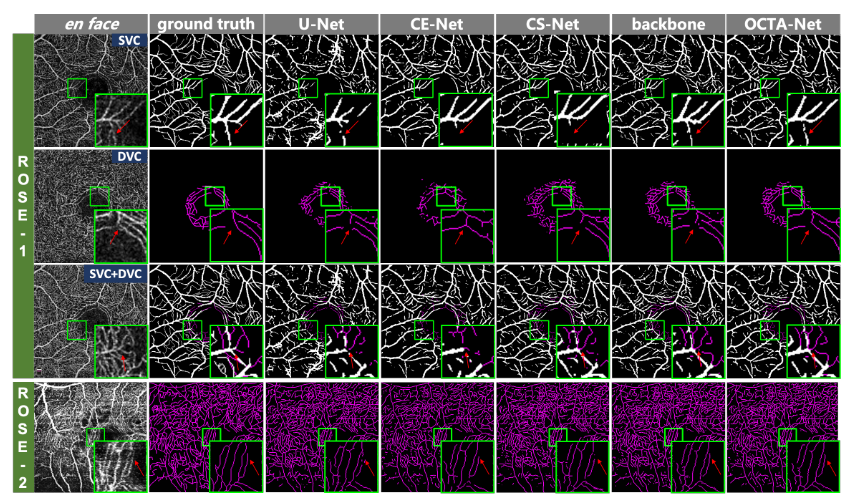
OCTA数据集(Rose)+ OCTA-Net
ROSE: A Retinal OCT-Angiography(视网膜眼底相干光层析血管成像术) Vessel Segmentation(血管分割) Dataset and New Model 论文:ROSE: A Retinal OCT-Angiography Vessel Segmentation Dataset and New Model 代码和数据集:ROSE1&2 - 医疗影像/眼…...
java Spring Boot 手动启动热部署
好 接下来 我们讲一个对开发非常重要的东西 热部署 因为 我们在开发过程中总会希望快点看到效果 或者 你的企业项目一般很大很复杂,重启是一件非常麻烦的事 或者你在和前端同事联调,有一点小问题 你改完就要重启 前端还得等你,非常不友好 那…...
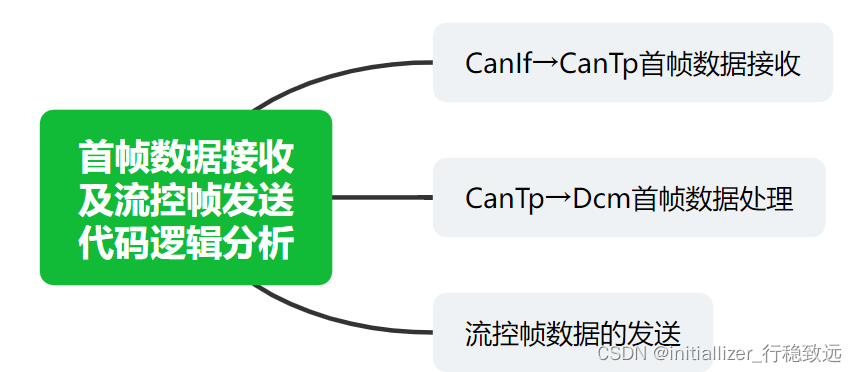
Autosar诊断实战系列20-UDS首帧数据接收及流控帧发送代码级分析
本文框架 前言1. 长帧数据的首帧接收2. 首帧数据的处理及流控帧发送2.1 首帧数据的处理2.2 流控帧数据的发送前言 在本系列笔者将结合工作中对诊断实战部分的应用经验进一步介绍常用UDS服务的进一步探讨及开发中注意事项, Dem/Dcm/CanTp/Fim模块配置开发及注意事项,诊断与Bs…...

C/C++ 数据结构 - 队列
1.队列 https://blog.csdn.net/LiuBo_01/article/details/80412290 1 #include <stdio.h>2 #include <stdlib.h>3 4 typedef struct Node5 {6 int data;7 struct Node* next;8 }N;9 10 typedef struct11 {12 N* front;13 N* rear;14 }Q;15 16 //…...
免杀对抗-DLL劫持免杀
C&Py-DLL劫持-语言-调用加载 1.使用visual studio创建项目 2.将文件名重命名为.c后缀 3.将如下加载器代码生成dll文件 加载器代码: #include "pch.h" #include <Windows.h> #include <stdio.h> #include <string.h>#pragma comment…...

Anaconda添加channels后出现unexpected urllib3 DEBUG logging from conda-build
1.问题描述 anaconda更新之后添加channels后出现bug: (base) ~/zlib-feedstock % conda build recipe 2>&1 | tee out ... INFO:conda_build.metadata:Attempting to finalize metadata for libzlib DEBUG:urllib3.connectionpool:Starting new HTTPS connection (1):…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
