Java数据结构中二叉树的深度解析及常见OJ题
本篇文章讲述Java数据结构中关于二叉树相关知识及常见的二叉树OJ题做法讲解(包含非递归遍历二叉树)
目录
一、二叉树
1.1二叉树概念
1.2特殊的二叉树
1.3二叉树性质
1.4二叉树基本性质定理题
1.5二叉树遍历基本操作
1.6二叉树遍历的前中后非递归写法
1.7二叉树有关的基本操作
二、二叉树常见的OJ题
2.1相同的树
2.2对称二叉树
2.3反转二叉树
2.4二叉树的公共祖先
2.5二叉树的层序遍历
2.6根据二叉树前序与中序序列构造二叉树
一、二叉树
1.1二叉树概念
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。3. 二叉树不存在度大于2的结点
4. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
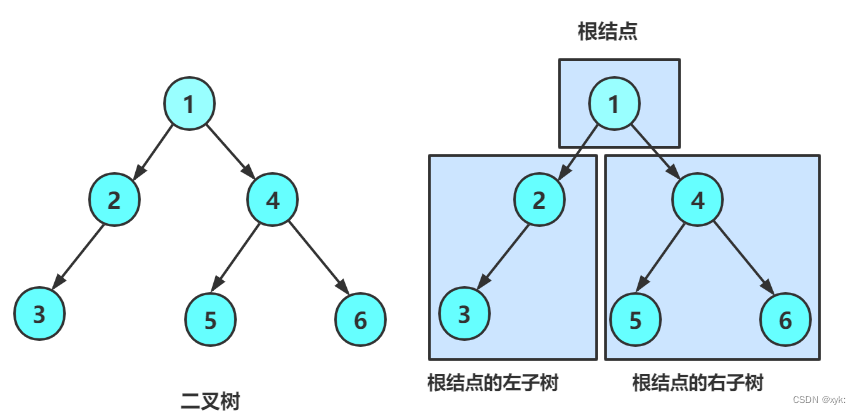

1.2特殊的二叉树
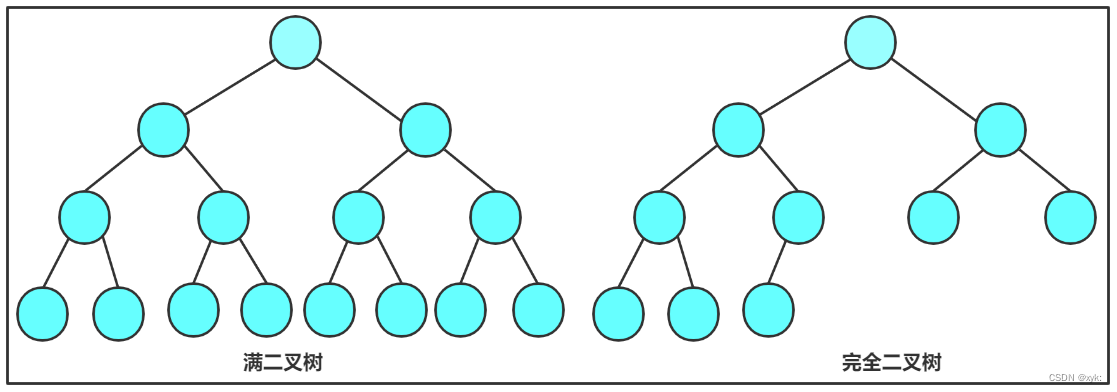
1. 满二叉树: 一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
2. 完全二叉树: 完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
1.3二叉树性质
1. 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有2^i-1 (i>0)个结点。
2. 若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是 2^k-1(k>=0)。
3. 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1。
4. 具有n个结点的完全二叉树的深度k为log2(n+1)上取整。
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
- 若2i+1<n,左孩子序号:2i+1,否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,否则无右孩子
6.当完全二叉树有偶数个节点时,n1 = 1;
7.当完全二叉树有奇数个节点时,n1 = 0;
8.n层k叉树共有节点(k^n-1)/ (k-1);
1.4二叉树基本性质定理题
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( B)
A 不存在这样的二叉树
B 200
C 198
D 199
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为(A )
A n
B n+1
C n-1
D n/23.一个具有767个节点的完全二叉树,其叶子节点个数为(B)
A 383
B 384
C 385
D 386
4.一棵完全二叉树的节点数为531个,那么这棵树的高度为(B )
A 11
B 10
C 8
D 12
1.5二叉树遍历基本操作
二叉树的存储结构分为:顺序存储和类似于链表的链式存储。
- 代码实现:
- NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。
- LNR:中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。
- LRN:后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点。
public class TestBinaryTree {static class TreeNode {public char val;public TreeNode left;//左孩子的引用public TreeNode right;//右孩子的引用public TreeNode(char val) {this.val = val;}}/*** 创建一棵二叉树 返回这棵树的根节点** @return*/public TreeNode createTree() {TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');A.left = B;A.right = C;B.left = D;B.right = E;C.left = F;C.right = G;E.right = H;//this.root = A;return A;}// 前序遍历public void preOrder(TreeNode root) {if (root == null) {return;}System.out.println(root.val + " ");preOrder(root.left);preOrder(root.right);}// 中序遍历void inOrder(TreeNode root) {if (root == null) {return;}inOrder(root.left);System.out.println(root.val + " ");inOrder(root.right);}// 后序遍历void postOrder(TreeNode root) {if (root == null) {return;}inOrder(root.left);inOrder(root.right);System.out.println(root.val + " ");}1.6二叉树遍历的前中后非递归写法
//前序遍历非递归public List<Integer> PreOrder(TreeNode root){List<Integer> list = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;while (cur != null || !stack.isEmpty()){while (cur != null){list.add(cur.val);stack.push(cur);cur = cur.left;}cur = stack.pop();cur = cur.right;}return list;}//中序遍历非递归public List<Integer> InorderTravelSal(TreeNode root){if (root == null){return new ArrayList<>();}List<Integer> list = new ArrayList<>();LinkedList<TreeNode> stack = new LinkedList<>();TreeNode cur = root;while (cur != null || !stack.isEmpty()) {while (cur != null) {stack.push(cur);cur = cur.left;}cur = stack.pop();list.add(cur.val);cur = cur.right;}return list;}//后序遍历非递归public List<Integer> PostOrder(TreeNode root){if (root == null){return new ArrayList<>();}List<Integer> list = new ArrayList<>();Deque<TreeNode> stack = new LinkedList<>();TreeNode cur = root;TreeNode prev = null;while (cur != null || !stack.isEmpty()){while (cur != null){stack.push(cur);cur = cur.left;}TreeNode node = stack.peek();if (node.right == null || node.right == prev){list.add(node.val);stack.pop();prev = node;}else {cur = cur.right;}}return list;}1.7二叉树有关的基本操作
/*** 获取树中节点的个数:遍历思路*/void size(TreeNode root) {if (root == null) {return;}nodeSize++;size(root.left);size(root.right);}/*获取叶子节点的个数:子问题*/int getLeafNodeCount2(TreeNode root) {if (root == null) {return 0;}if (root.left == null && root.right == null) {return 1;}int leftSize = getLeafNodeCount2(root.left);int rightSize = getLeafNodeCount2(root.right);return leftSize + rightSize;}/*获取第K层节点的个数*/int getKLevelNodeCount(TreeNode root, int k) {if (root == null) {return 0;}if (k == 1) {return 1;}int leftSize = getKLevelNodeCount(root.left, k - 1);int rightSize = getKLevelNodeCount(root.right, k - 1);return leftSize + rightSize;}/*获取二叉树的高度时间复杂度:O(N)*/public int maxDepth(TreeNode root) {if (root == null) {return 0;}int leftHeight = maxDepth(root.left);int rightHeight = maxDepth(root.right);return (leftHeight > rightHeight) ?(leftHeight + 1) : (rightHeight + 1);}// 检测值为value的元素是否存在TreeNode find(TreeNode root, char val) {if (root == null) {return null;}if (root.val == val) {return root;}TreeNode leftTree = find(root.left, val);if (leftTree != null) {return leftTree;}TreeNode rightTree = find(root.right, val);if (rightTree != null) {return rightTree;}return null;//没有找到}二、二叉树常见的OJ题
2.1相同的树
100. 相同的树 - 力扣(LeetCode)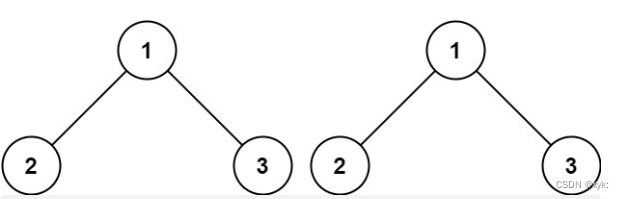
class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {if(p == null && q == null){return true;}if(p != null && q == null || p == null && q != null){return false;}if(p.val != q.val){return false;}return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);}
}2.2对称二叉树
101. 对称二叉树 - 力扣(LeetCode)
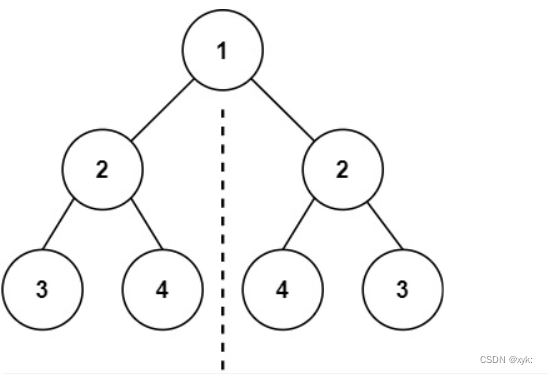
class Solution {public boolean isSymmetric(TreeNode root) {if (root == null){return true;}return isSymmetricChild(root.left,root.right);}public boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree){if (leftTree != null && rightTree == null ||leftTree == null && rightTree != null){return false;}if (leftTree == null && rightTree == null){return true;}if (leftTree.val != rightTree.val){return false;}return isSymmetricChild(leftTree.left,rightTree.right) &&isSymmetricChild(leftTree.right,rightTree.left);}
}与上一道相同的树原理一致。
2.3反转二叉树
226. 翻转二叉树 - 力扣(LeetCode)
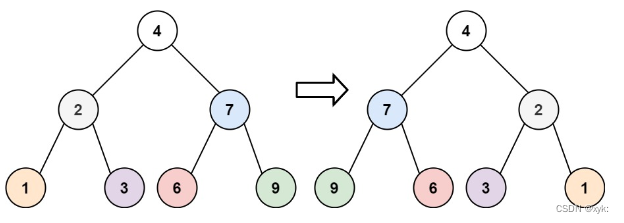
class Solution {public TreeNode invertTree(TreeNode root) {if (root == null){return null;}TreeNode tmp = root.left;root.left = root.right;root.right = tmp;invertTree(root.left);invertTree(root.right);return root;}
}注意将子节点的每个节点都要反转
2.4二叉树的公共祖先
最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)
236. 二叉树的最近公共祖先 - 力扣(LeetCode)
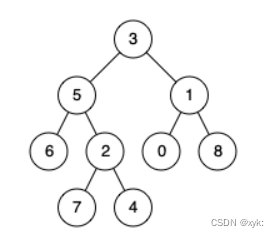
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(root == null){return null;}if(root == q || root == p){return root;}TreeNode leftRet = lowestCommonAncestor(root.left,p,q);TreeNode rightRet = lowestCommonAncestor(root.right,p,q);if(leftRet != null && rightRet != null){return root;}else if(leftRet != null){return leftRet;}else if(rightRet != null){return rightRet;}return null;}
}注意在左右子树中寻找节点,如果找到并返回节点,否则返回空
2.5二叉树的层序遍历
102. 二叉树的层序遍历 - 力扣(LeetCode)
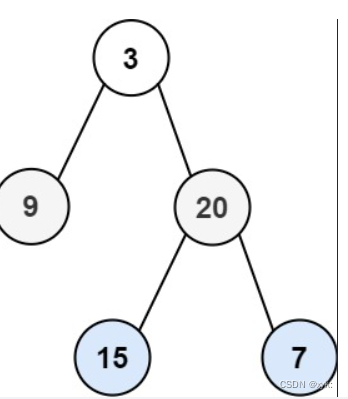
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> list = new ArrayList<>();if (root == null) {return list;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {int size = queue.size();List<Integer> tmp = new ArrayList<>();while (size > 0) {TreeNode cur = queue.poll();tmp.add((int) cur.val);if (cur.left != null) {queue.offer(cur.left);}if (cur.right != null) {queue.offer(cur.right);}size--;}list.add(tmp);}return list;}}本题需要注意层序遍历要使用队列,先进先出。
2.6根据二叉树前序与中序序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点
105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)
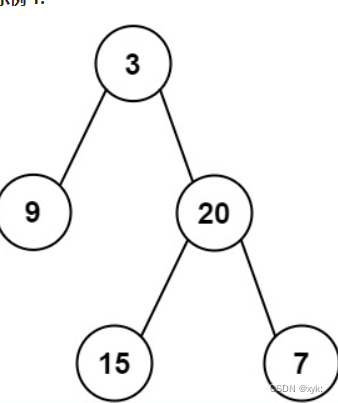
class Solution {public TreeNode buildTree(int[] preorder, int[] inorder) {return buildTreechild(preorder,inorder,0,inorder.length-1);}int i = 0;public TreeNode buildTreechild(int[] preorder,int[] inorder,int inbegin,int inend){if(inbegin > inend){return null;}TreeNode root = new TreeNode(preorder[i]);int rootIndex = findIndex(inorder,inbegin,inend,preorder[i]);i++;root.left = buildTreechild(preorder,inorder,inbegin,rootIndex-1); root.right = buildTreechild(preorder,inorder,rootIndex+1,inend);return root; }public int findIndex(int[] inorder,int inbegin,int inend,int key){for(int i = inbegin;i <= inend;i++){if(inorder[i]==key){return i;}}return -1;}
}本题需要注意的点是只有给出前序或后续序列才能确定中序中根的位置
相关文章:

Java数据结构中二叉树的深度解析及常见OJ题
本篇文章讲述Java数据结构中关于二叉树相关知识及常见的二叉树OJ题做法讲解(包含非递归遍历二叉树) 目录 一、二叉树 1.1二叉树概念 1.2特殊的二叉树 1.3二叉树性质 1.4二叉树基本性质定理题 1.5二叉树遍历基本操作 1.6二叉树遍历的前中后非递归写法 1.7…...

算法顶级比赛汇总
可参赛的算法比赛 阿里云天池大数据竞赛 时间:每年各个季度很多类型都会出题(比赛总时间大概为两个月) 内容:各个类型的算法题都会出、奖金上万不等 形式:在线提交(提交后在线检查结果)、离线…...

Android MVI框架搭建与使用
MVI框架搭建与使用前言正文一、创建项目① 配置AndroidManifest.xml② 配置app的build.gradle二、网络请求① 生成数据类② 接口类③ 网络请求工具类三、意图与状态① 创建意图② 创建状态四、ViewModel① 创建存储库② 创建ViewModel③ 创建ViewModel工厂五、UI① 列表适配器②…...
第九节 使用设备树实现RGB 灯驱动
通过上一小节的学习,我们已经能够编写简单的设备树节点,并且使用常用的of 函数从设备树中获取我们想要的节点资源。这一小节我们带领大家使用设备树编写一个简单的RGB 灯驱动程序,加深对设备树的理解。 实验说明 本节实验使用到STM32MP1 开…...

Ubuntu 系统下Docker安装与使用
Ubuntu 系统下Docker安装与使用Docker安装与使用Docker安装安装环境准备工作系统要求卸载旧版本Ubuntu 14.04 可选内核模块Ubuntu 16.04 使用 APT 安装安装 Docker CE使用脚本自动安装启动 Docker CE建立 docker 用户组测试 Docker 是否安装正确镜像加速Docker使用拉取镜像创建…...
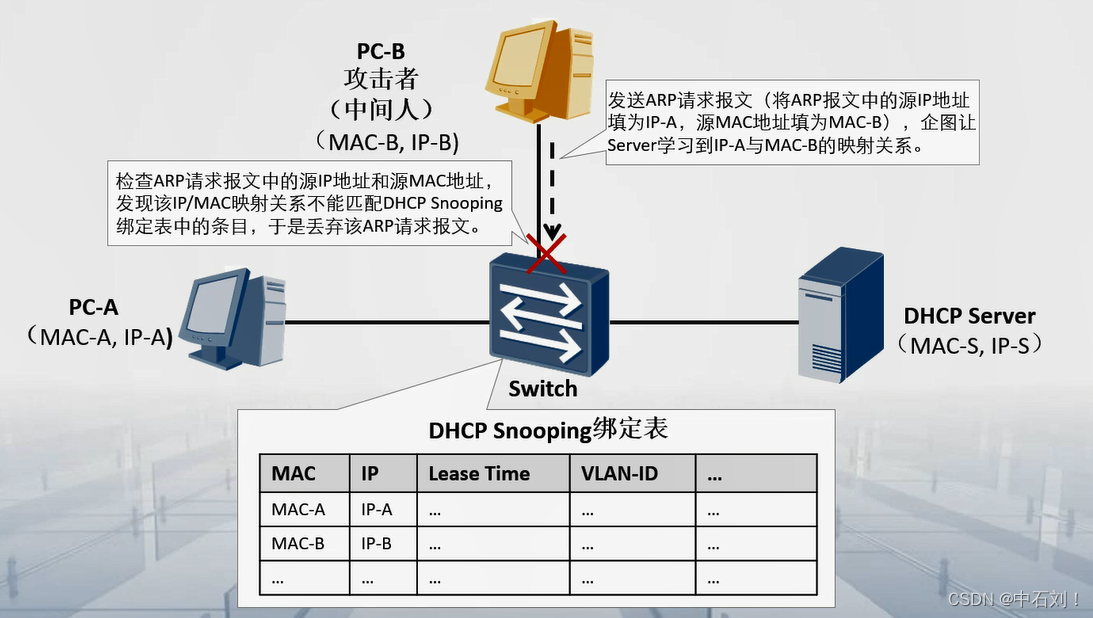
DHCP安全及防范
DHCP安全及防范DHCP面临的威胁DHCP饿死攻击仿冒DHCP Server攻击DHCP中间人攻击DHCP Snooping技术的出现DHCP Snooping防饿死攻击DHCP Snooping防止仿冒DHCP Server攻击DHCP Snooping防止中间人攻击DHCP Snooping防止仿冒DHCP报文攻击DHCP面临的威胁 网络攻击无处不在ÿ…...

【流畅的python】第一章 Python数据模型
文章目录第一章 Python 数据模型1.1 python风格的纸牌1.2 如何使用特殊方法-通过创建一个向量类的例子1.3 特殊方法汇总第一章 Python 数据模型 python最好的品质是一致性 python解释器碰到特殊句法时,会使用特殊方法去激活一些基本的对象操作 这些特殊的方法以两个…...
from文件突然全部变为类cs右击无法显示设计界面
右击也不显示查看设计器 工程文件 .csproj中将 <Compile Include"OperatorWindows\Connection.cs" /> <Compile Include"OperatorWindows\Connection.Designer.cs"> <DependentUpon>Connection.cs</DependentUpon> &…...

使用arthas中vmtool命令查看spring容器中对象的某个属性
场景: 线上环境我想查看spring中容器某个对象的属性值 vmtool命令 方式一: vmtool --action getInstances -c [类加载器的hash] --className [目标类全路径] --limit 10 -x 2 实例:查询该类的全部属性情况(该类是一个spri…...

四种幂等性解决方案
什么是幂等性? 幂等是一个数学与计算机学概念,在数学中某一元运算为幂等时,其作用在任一元素两次后会和其作用一次的结果相同。 在计算机中编程中,一个幂等操作的特点是其任意多次执行所产生的影响均与一次执行的影响相同。 幂等…...

【Nacos】Nacos配置中心客户端配置更新源码分析
上文我们说了服务启动的时候从远程Nacos服务端拉取配置,这节我们来说下Nacos服务端配置的变动怎么实时通知到客户端,首先需要注册监听器。 注册监听器 NacosContextRefresher类会监听应用启动发布的ApplicationReadyEvent事件,然后进行配置…...

按钮防抖与节流-vue2
防抖与节流,应用场景有很多,例如:禁止重复提交数据的场景、搜索框输入搜索条件,待输入停止后再开始搜索。 防抖 点击button按钮,设置定时器,在规定的时间内再次点击会重置定时器重新计时,在规定…...

PyTorch学习笔记:nn.SmoothL1Loss——平滑L1损失
PyTorch学习笔记:nn.SmoothL1Loss——平滑L1损失 torch.nn.SmoothL1Loss(size_averageNone, reduceNone, reductionmean, beta1.0)功能:创建一个平滑后的L1L_1L1损失函数,即Smooth L1: l(x,y)L{l1,…,lN}Tl(x,y)L\{l_1,\dots,l…...
2年时间,涨薪20k,想拿高薪还真不能老老实实的工作...
2016年开始了我的测试生活。 2016年刚到公司的时候,我做的是测试工程师。做测试工程师是我对自己的职业规划。说实话,我能得到这份工作真的很高兴。 来公司的第一个星期,因为有一个项目缺人,所以部门经理提前结束了我的考核期&a…...

Spark - Spark SQL中RBO, CBO与AQE简单介绍
Spark SQL核心是Catalyst, Catalyst执行流程主要分4个阶段, 语句解析, 逻辑计划与优化, 物理计划与优化, 代码生成 前三个阶段都由Catalyst负责, 其中, 逻辑计划的优化采用RBO思路, 物理计划的优化采用CBO思路 RBO (Rule Based Optimization) 基于规则优化, 通过一系列预定好…...

NeurIPS/ICLR/ICML AI三大会国内高校和企业近年中稿量完整统计
点击文末公众号卡片,找对地方,轻松参会。 近日,有群友转发了一张网图,统计了近年来中国所有单位在NeurIPS、ICLR、ICML论文情况。原图如下: 中稿数100: 清华(1) 北大(2) 占比:22.6%。 累计数…...
Android IO 框架 Okio 的实现原理,到底哪里 OK?
本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 提问。 前言 大家好,我是小彭。 今天,我们来讨论一个 Square 开源的 I/O 框架 Okio,我们最开始接触到 Okio 框架还是源于 Square 家的 OkHttp 网络…...

一文讲解Linux 设备模型 kobject,kset
设备驱动模型 面试的时候,有面试官会问,什么是Linux 设备驱动模型?你要怎么回答? 这个问题,突然这么一问,可能你会愣住不知道怎么回答,因为Linux 设备驱动模型是一个比较整体的概念࿰…...

linux配置密码过期的安全策略(/etc/login.defs的解读)
长期不更换密码很容易导致密码被破解,而linux的密码过期安全策略主要在/etc/login.defs中配置。一、/etc/login.defs文件的参数解读1、/etc/login.defs文件的内容示例[rootlocalhost ~]# cat /etc/login.defs # # Please note that the parameters in this configur…...

c_character_string 字符串----我认真的弄明白了,也希望你们也是。
字符串 1. 字符串长度strlen 1.1strlen 函数介绍 size_t strlen ( const char * str );strlen ——string length strlen 的头文件是 #include <string.h> 参数指向的字符串必须要以 ‘\0’ 结束。 strlen 是求字符串长度的函数,统计的是字符串中\0之前出现…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
