6.Tensors For Beginners-What are Convector
Covectors (协向量)
What‘s a covector
Covectors are “basically” Row Vectors
在一定程度上,可认为 协向量 基本上就像 行向量。
但不能简单地认为 这就是列向量进行转置!
行向量 和 列向量 是根本不同类型的对象。
(处理正交基时,将列向量转置成行向量的做法是正确的,但在其他坐标系中不是这样)
要理解这个,需将 行向量视为函数,
因此,可将行向量 视为 列向量上的函数,row vectors are functions on (column) vectors
eg:y=f(x) x就是输入
行向量 [ 2,1 ]是函数,列向量 [ -3 ; 4 ]是函数的输入,
要得到函数的输出值,只需对该行向量和列向量进行矩阵乘法 或“点积”
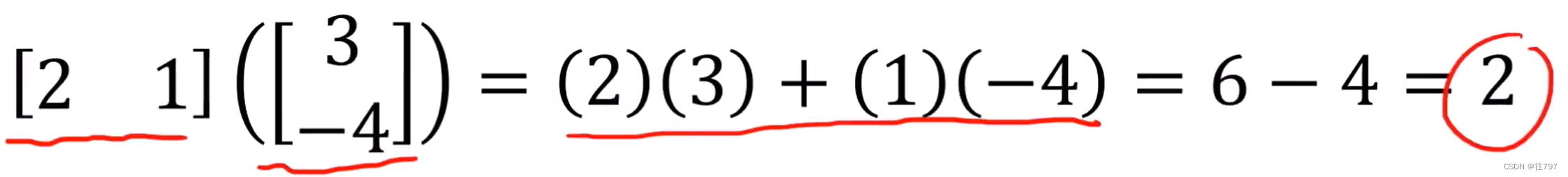
现如果,有 任意通用的协向量α 作用于 任意通用向量v上,
则可通过两向量的点积来获取输出值,

因此,最终我们应将 行向量 视为 【从某个向量空间V 中 获取输入并返回实数或“标量”】的函数

这些行向量函数是如何工作的?
假设一行向量 作用于两个相加的向量输入上,可通过两种方式求,
(1.分配律--我认为就是分配律的体现)
将行向量分配给每个输入,然后将结果相加,输出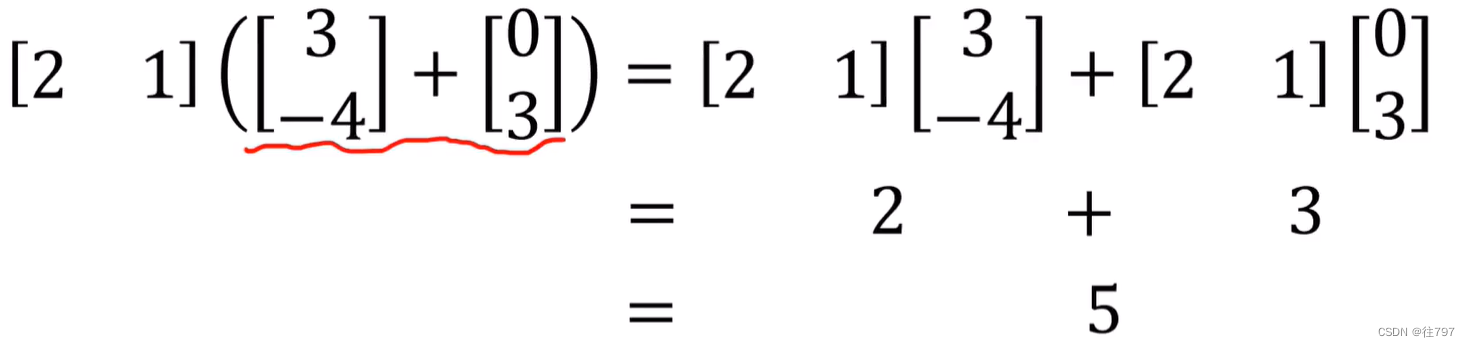
(2.结合律--个人理解)
将输入相加,再进行点积 
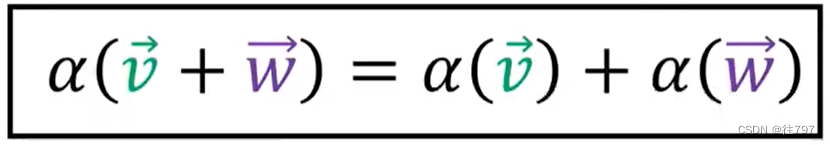
所以行向量作为函数 在这里有个属性:可以在之前添加输入;或在之后添加输出。会得到相同的结果
还有一个想法是:
若向量输入按某个数字进行缩放会怎样
同样有两种方法计算
1.可缩放输入向量,再进行点积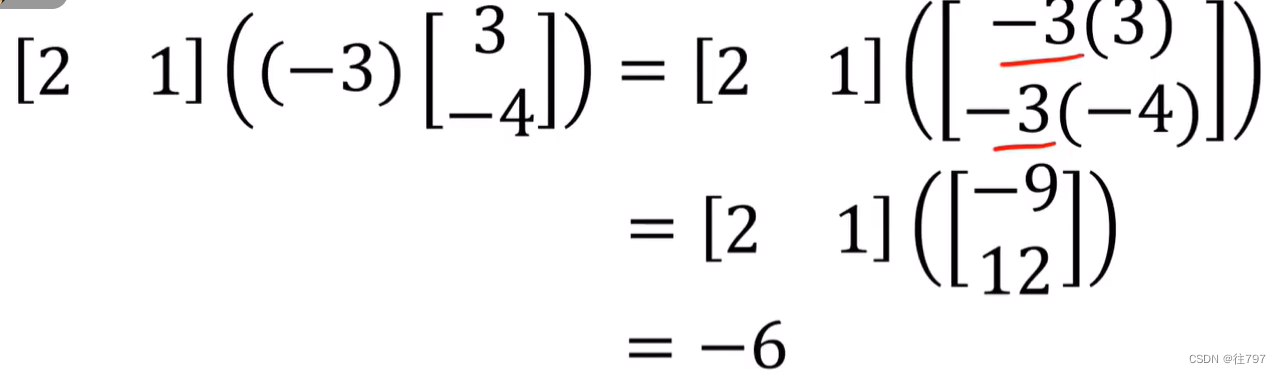
2.把缩放数 提到最前面,再计算行向量与列向量的点积,最后再缩放结果,
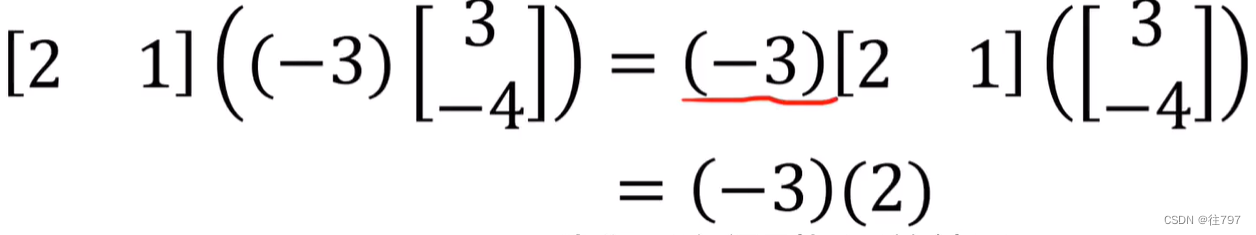
因此,作为函数的行向量具有这个属性:可缩放输入,或缩放输出,并得到相同的结果。
总而言之, 协向量是一个 函数,它接受一个向量并产生一个“标量”(或一个数字);它具有可添加输入或添加输出以获得相同答案的属性;并且它具有可按相同数量缩放输入或缩放输出并得到相同答案的属性。
这种能添加或缩放 输入或输出 并获得相同答案的行为 称为 “线性“。所以协向量是线性函数。

如何可视化协向量?
我们可以将普通向量可视化为箭头,我们可以对协向量做同样的事情,但对于可视化函数来说,这是件尴尬的事。
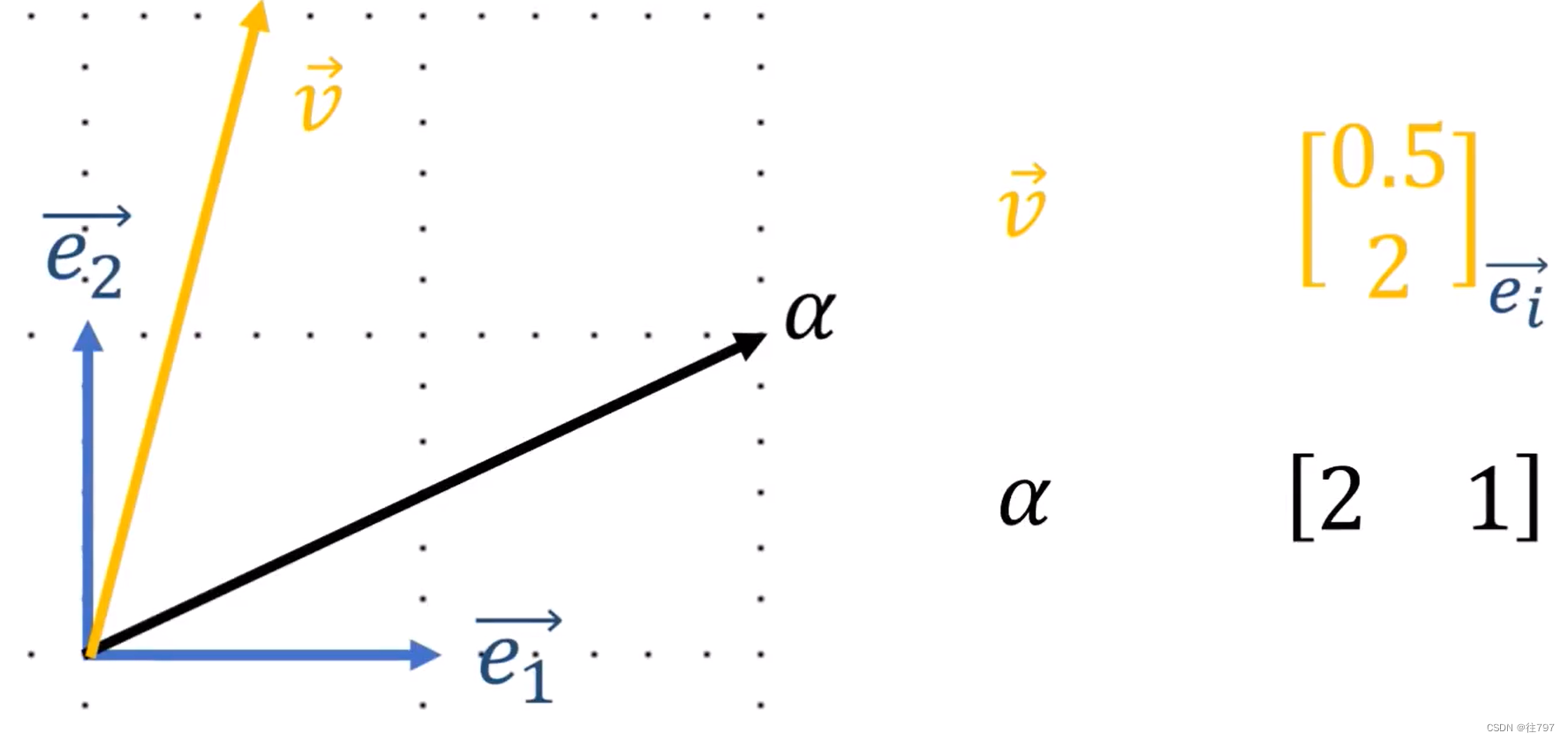
有一种更好的办法可视化协向量
首先将2D行向量视为两个变量x、y的函数,(x、y是输入)
在这个例子中,这个行向量 [ 2 , 1 ] 就可认为是一个函数:v,如何可视化 用两个变量产生一个输出 的函数 呢?
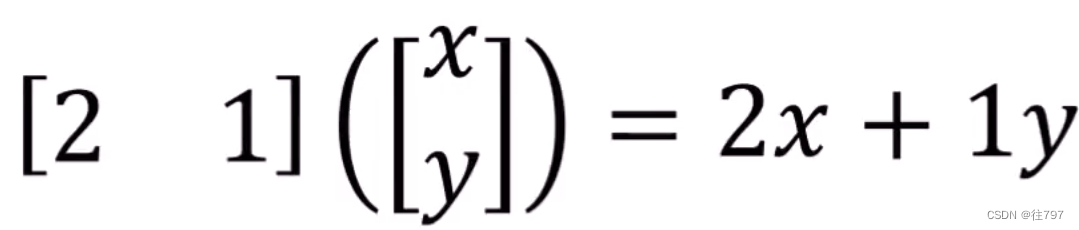
这与地形图有些相似,地形图上,同一海拔高度的都用一条线连起来。
同样地,我们给这个函数一个输出,就有一条线,
如 2x+1y = 0 确定一条线;
2x+1y = 1 确定一条线;
2x+1y = 2 确定一条线;
2x+1y = -1 确定一条线;
2x+1y = -2 确定一条线;
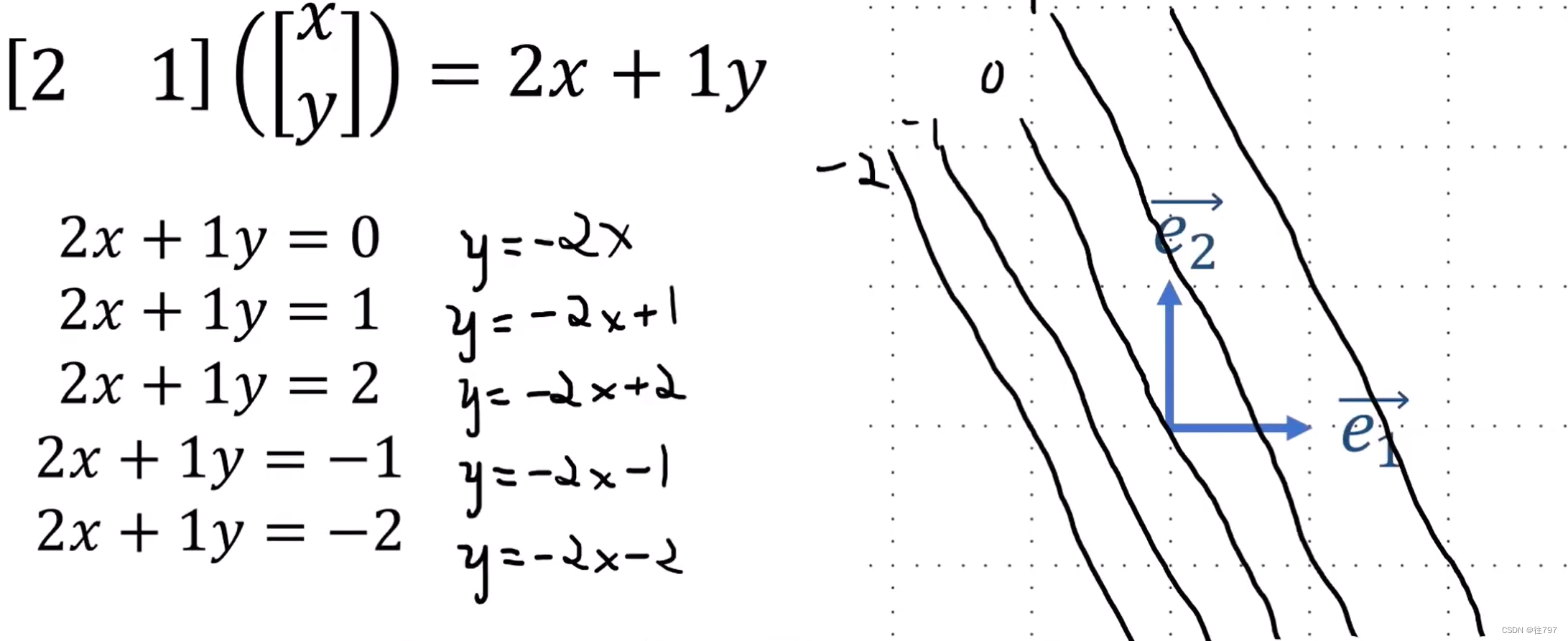
所以我们可将协向量【2,1】视为 一堆的直线:
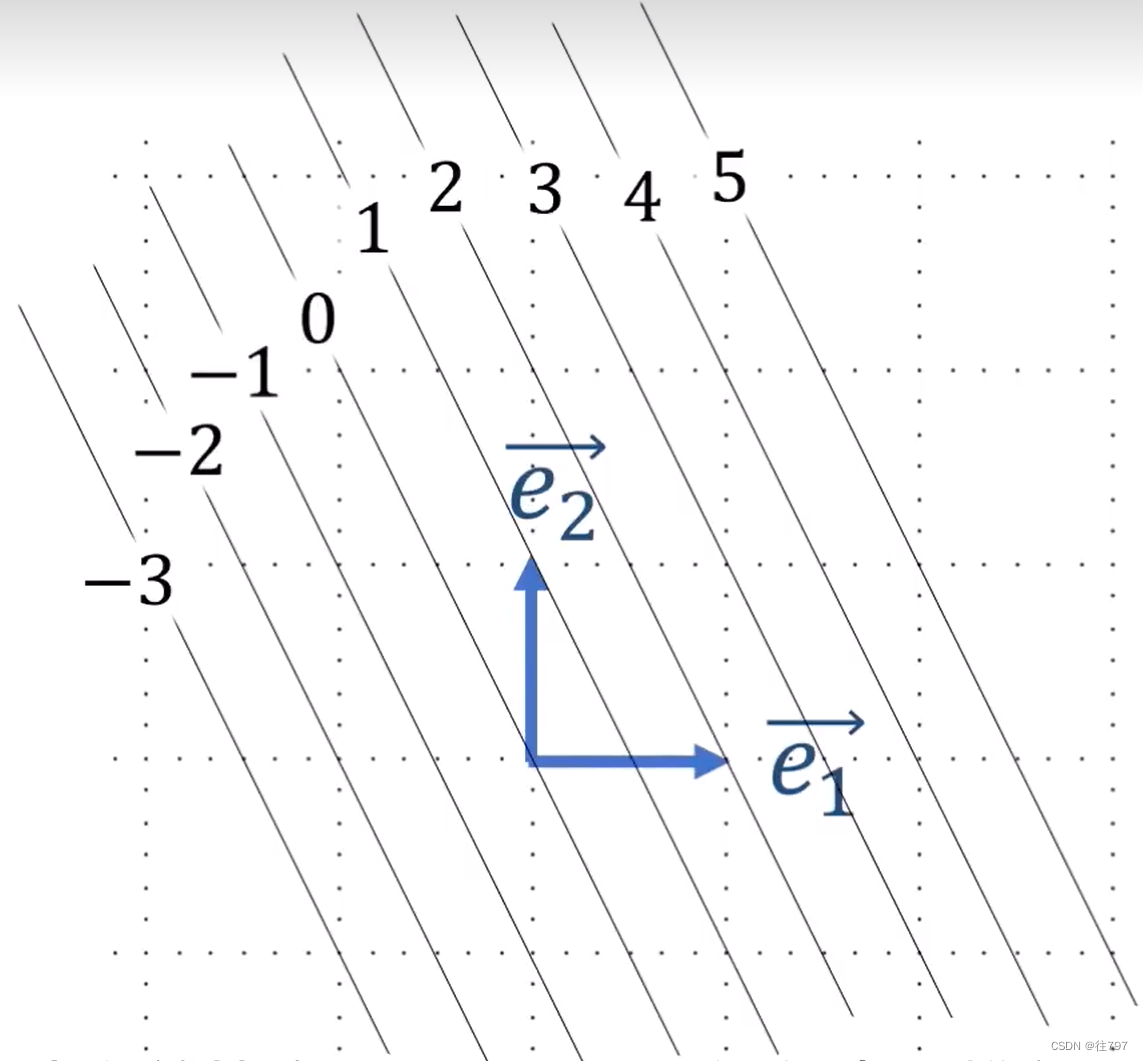
注意到,这些线 向右上角增加,可添加箭头提示增加的方向。
将行向量α=【2,1】绘制在图上的话,会发现 α 垂直于 所有的直线。

为什么会垂直?把【2,1】用【a,b】去进行证明,一个方向是 这些直线的方向相同,方向向量相同,用方向向量与α进行点乘; 另一个方向是 斜率,直线的斜率都一样(-a/b),α行向量作为直线的话,斜率是b/a,也可证明
所以我们可将协向量【2,1】视为 一堆的直线,而且这非常有用。
例子:
在这四个图中,协向量α相同,可视化为一堆线
在该协向量上, 有向量V指向不同的方向,
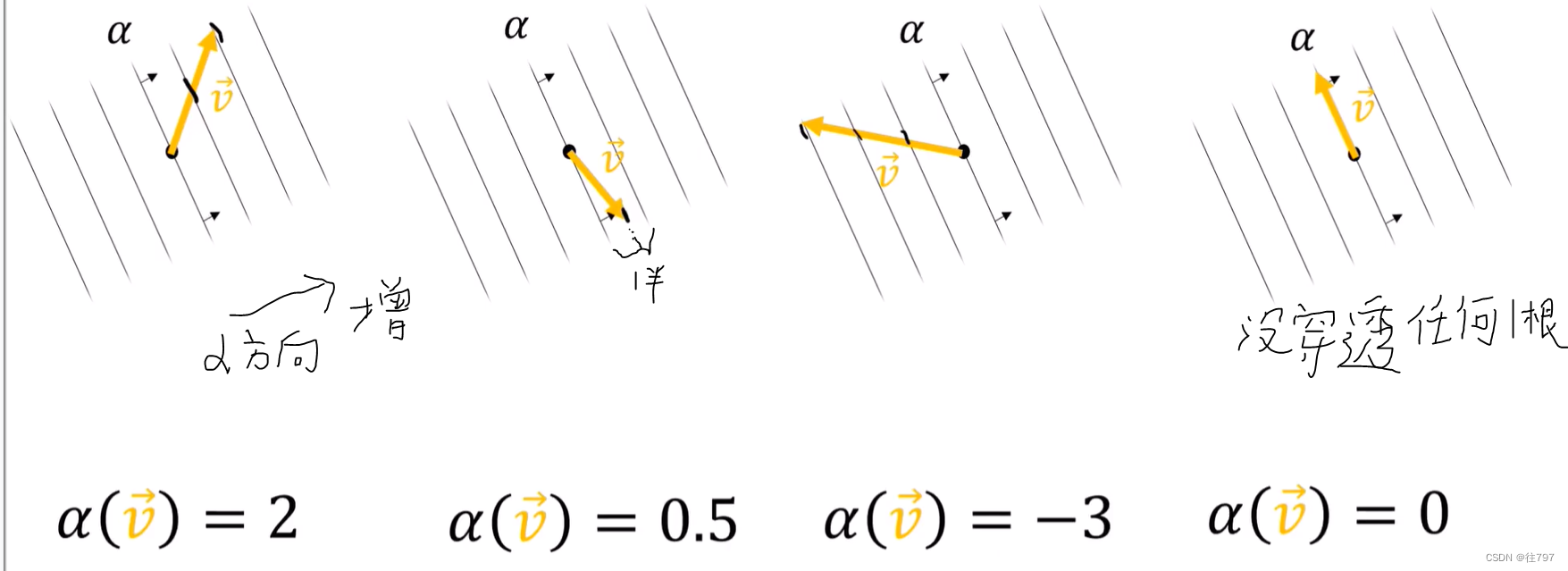
需要做的是,计算作用在向量V上的协向量α的数值,
记住:这一堆线中的每一条线都是代表一常量值的线,
因此,要获得作用在V上的α的值,需要做的是 计算V穿透的线的个数。
PS:这样计算真的好简单,但是对于编写成代码来计算的话,好像很难把,想不出头绪,能自己画出图,这样是最直观,但画图也不容易。
接着,修改协向量,获得新的协向量来进行计算
把协向量放大两倍
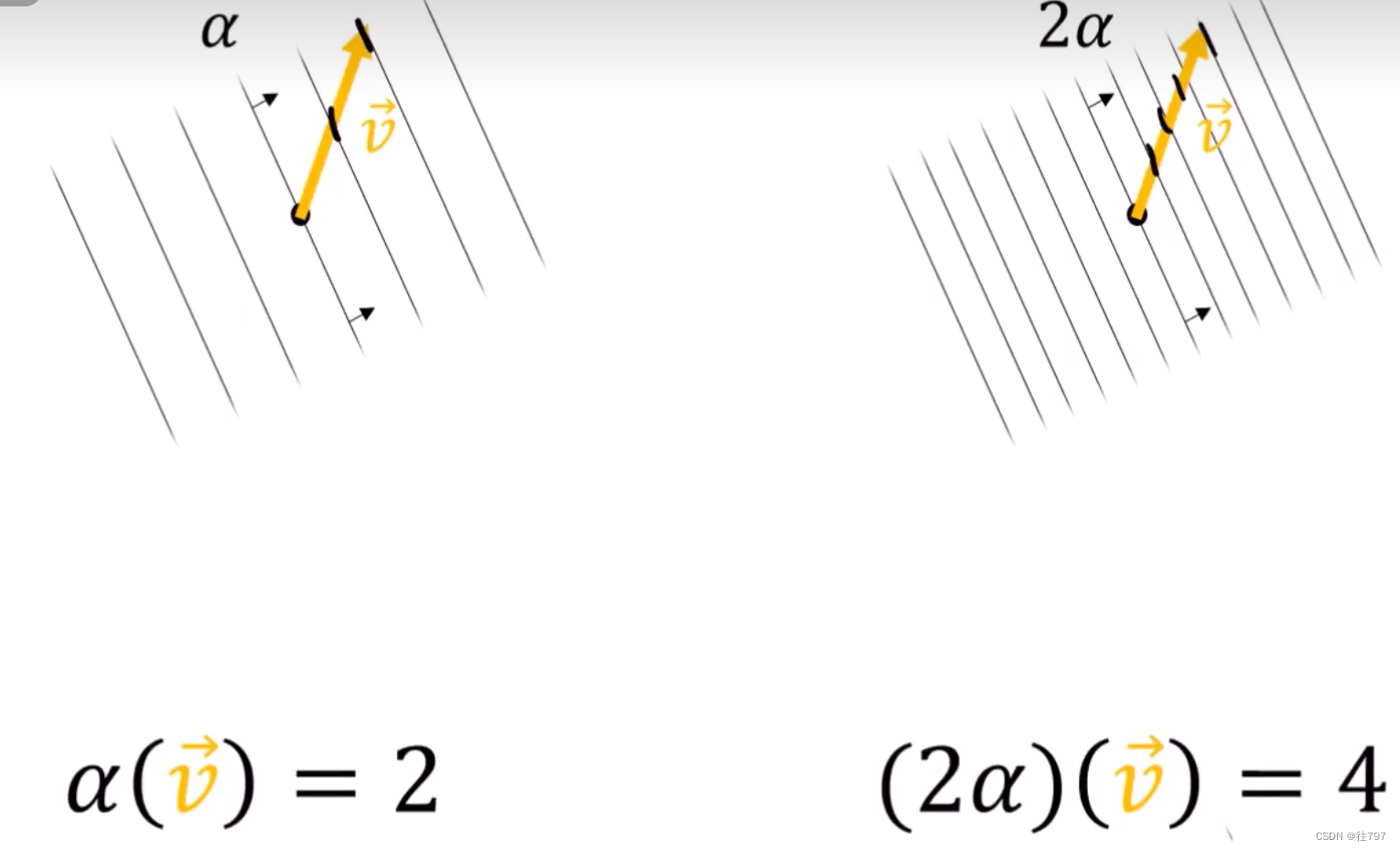
把协向量放大两倍,其实就是从 α 变为 2α , 如果你从式子上看的话, 能直接想到应该是结果放大两倍, 那么对应的输出结果应该放大两倍, 那对应图上,就是穿透的线要翻倍,则图要变密集,比原来密集一倍。
从 【a,b】*【x;y】上理解,ax+by函数,变为【2a,2b】*【x;y】= 2ax + 2by、ax+by = k---------y = -ax/b + k/b;
2ax+2by= k-------y= -ax/b + k/2b; 只是截距变啦,斜率没变, 所以截距影响线 的间距?
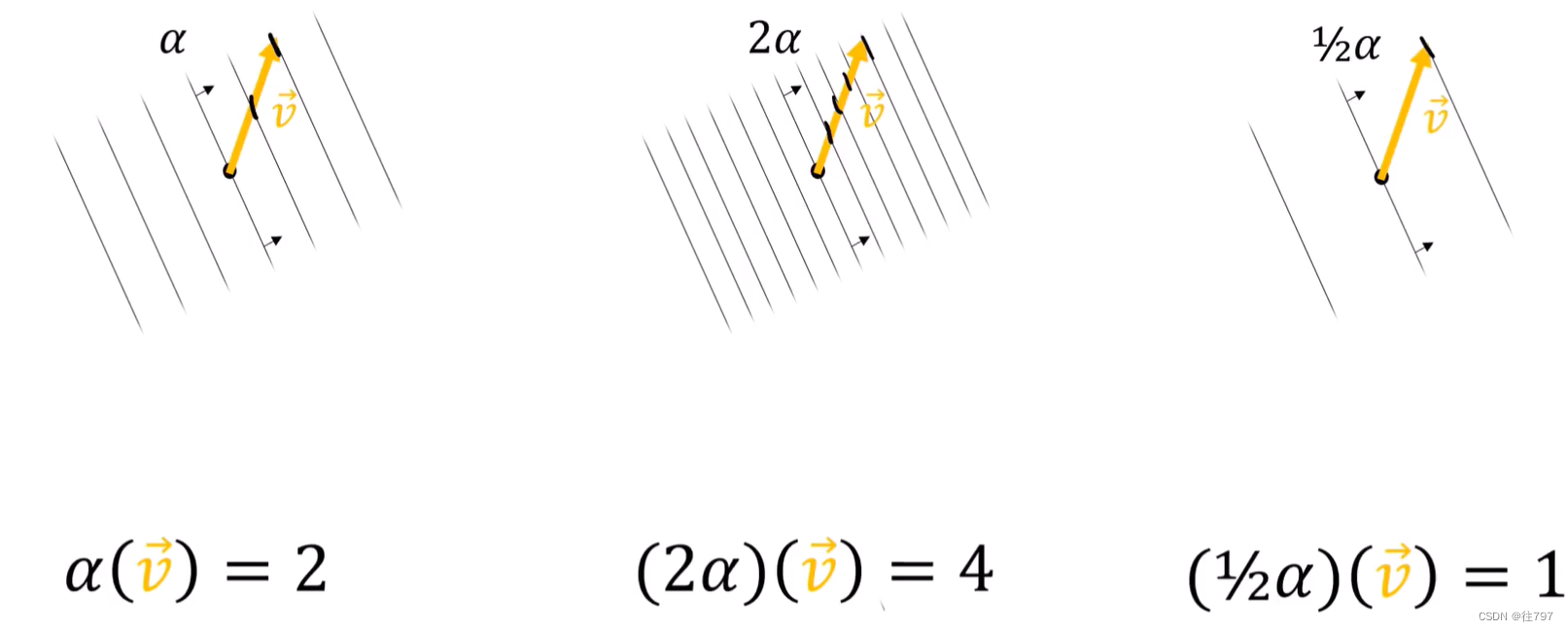
以上就是缩放协向量;
接着便是把协向量进行相加的情况,
β、γ两个协向量进行相加,如何画出β+γ的线?----------结果 在 β方向上与β具有相同的密度,在γ方向上与γ具有相同的密度。
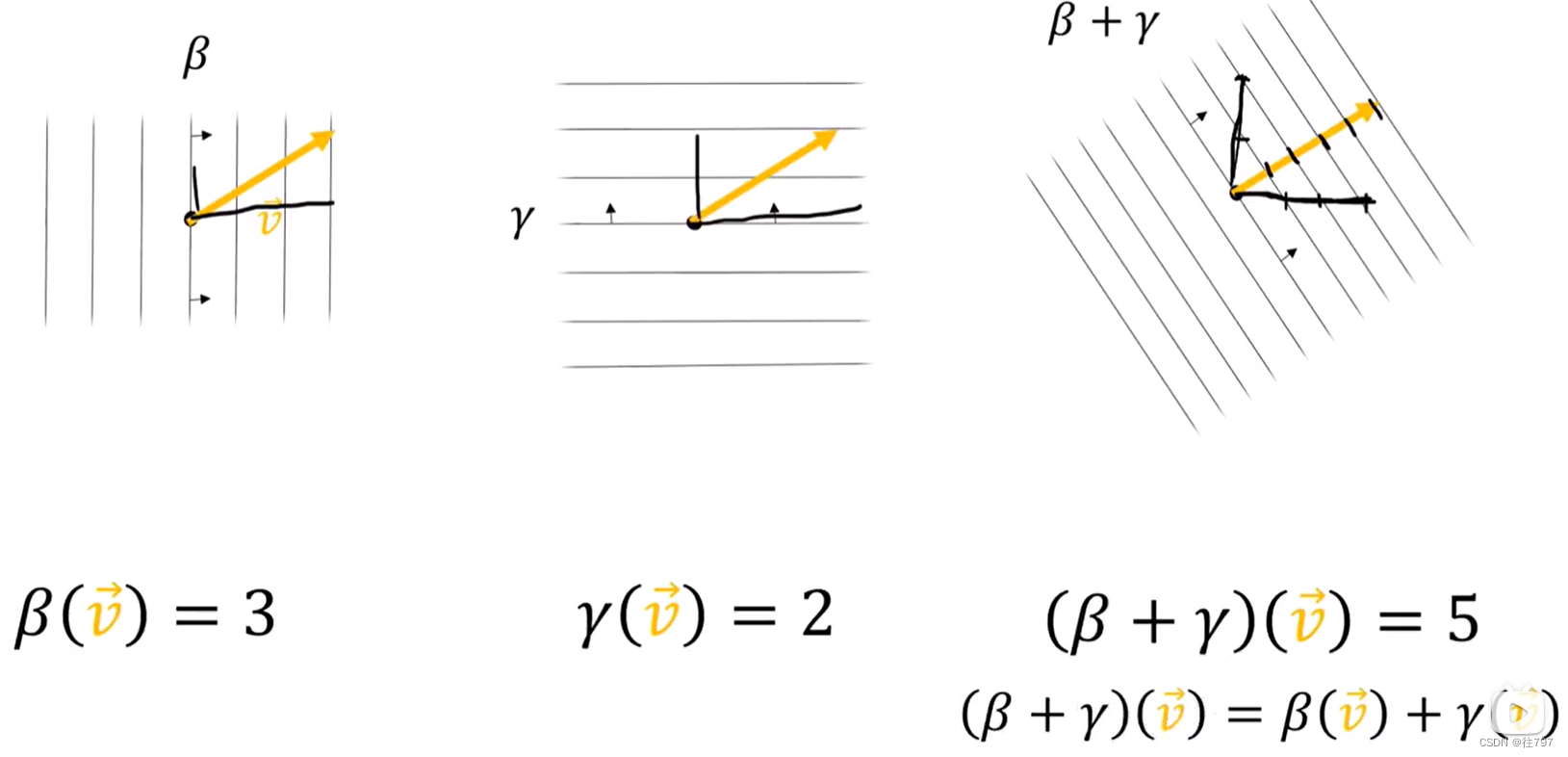
观察相加后的新协向量,V在β方向上的分量 同之前一样,穿透三根线,V在γ方向上的分量 同之前一样,穿透两根线。
从某种意义上说,β的水平密度为3,垂直密度为0;而γ的水平密度为0,垂直密度为2
而β+γ ,就是将两者结合在一起,水平密度:3+0=3;垂直密度:0+2 =2
而V在β+γ这个协向量上穿透5根线,其实就是原来的:V在β上穿透3根,在γ上穿透2根,加起来就是5根。,
其实从式子上理解的话,是非常容易理解的。
以上就证明,协向量具有合理的缩放和添加规则,
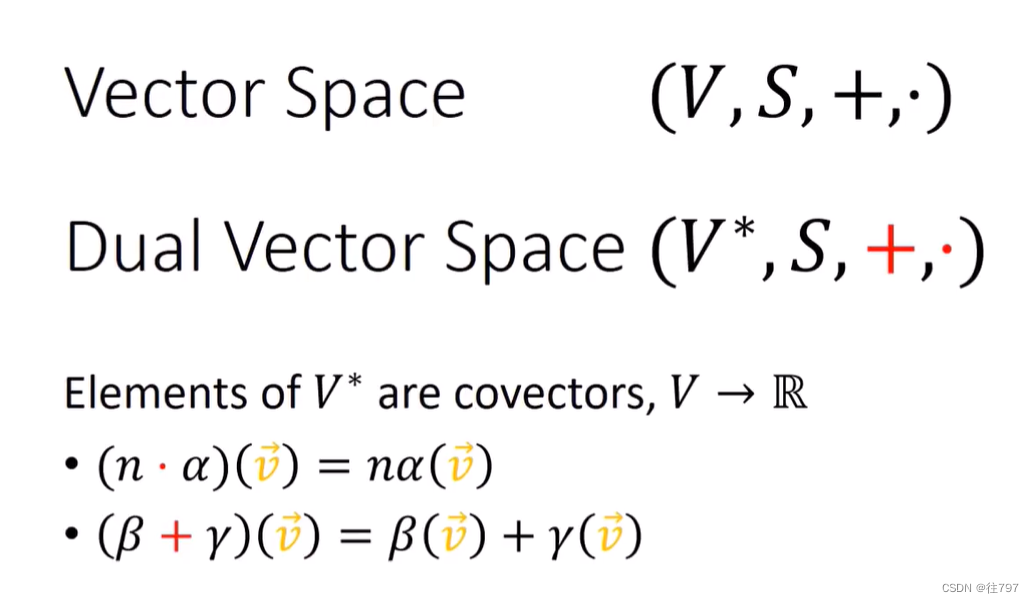
作用于向量V的所有covector 的集合形成一个新的向量空间,称为”对偶空间“,用 ” V* “表示,
有一组不同的添加规则,称为”red+“ ---- ” + “
有一组不同的缩放规则,称为”red·“------” · “
用不同颜色来表示这些规则的原因是 因为它们实际上是不同的规则,
黑色规则用于添加和缩放向量,就是用箭头表示的矢量所作规则;
红色规则用于添加和缩放协向量,像上面的例子那般,
V* 中的元素就是协向量,它们是 从V到实数的函数,
总结。协向量是从向量到实数的函数 , 这些函数具有可以添加和缩放输入 或 添加和缩放输出 以获得相同答案的属性。这就是所谓的”线性“,所以这些是线性函数。
作用在向量空间 V 上的所有协向量的集合形成 向量空间V*,这些协向量有自己的加法和缩放规则,可将协向量视为 一簇线,
+
相关文章:
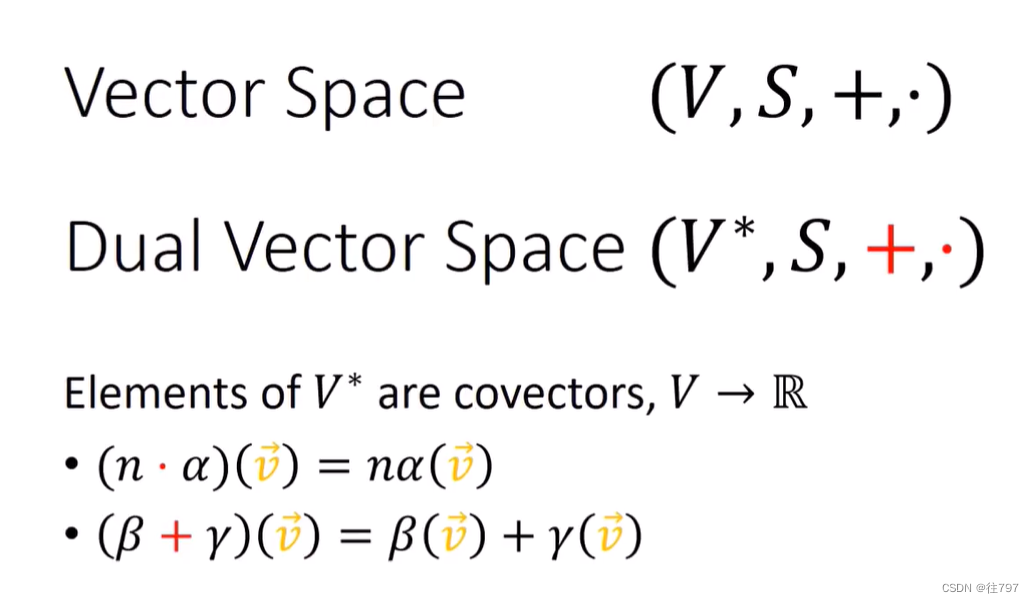
6.Tensors For Beginners-What are Convector
Covectors (协向量) What‘s a covector Covectors are “basically” Row Vectors 在一定程度上,可认为 协向量 基本上就像 行向量。 但不能简单地认为 这就是列向量进行转置! 行向量 和 列向量 是根本不同类型的对象。 …...
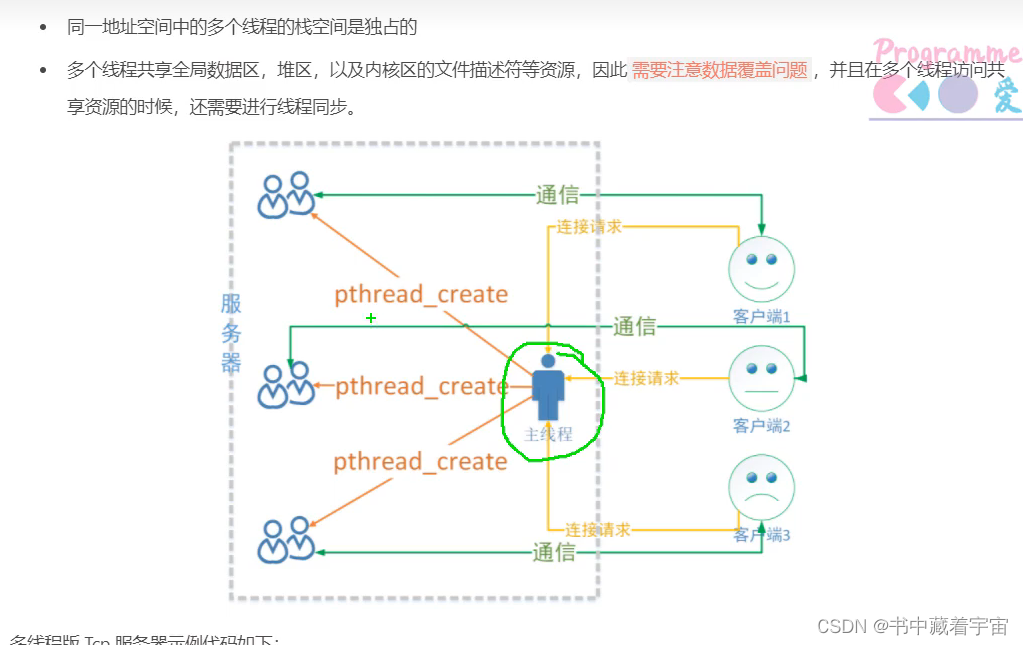
Linux多线程网络通信
思路:主线程(只有一个)建立连接,就创建子线程。子线程开始通信。 共享资源:全局数据区,堆区,内核区描述符。 线程同步不同步需要取决于线程对共享资源区的数据的操作,如果是只读就不…...

矩阵的c++实现(2)
上一次我们了解了矩阵的运算和如何使用矩阵解决斐波那契数列,这一次我们多看看例题,了解什么情况下用矩阵比较合适。 先看例题 1.洛谷P1939 【模板】矩阵加速(数列) 模板题应该很简单。 补:1<n<10^9 10^9肯定…...

RPC 框架之Thrift入门(一)
📋 个人简介 💖 作者简介:大家好,我是阿牛,全栈领域优质创作者。😜📝 个人主页:馆主阿牛🔥🎉 支持我:点赞👍收藏⭐️留言Ὅ…...
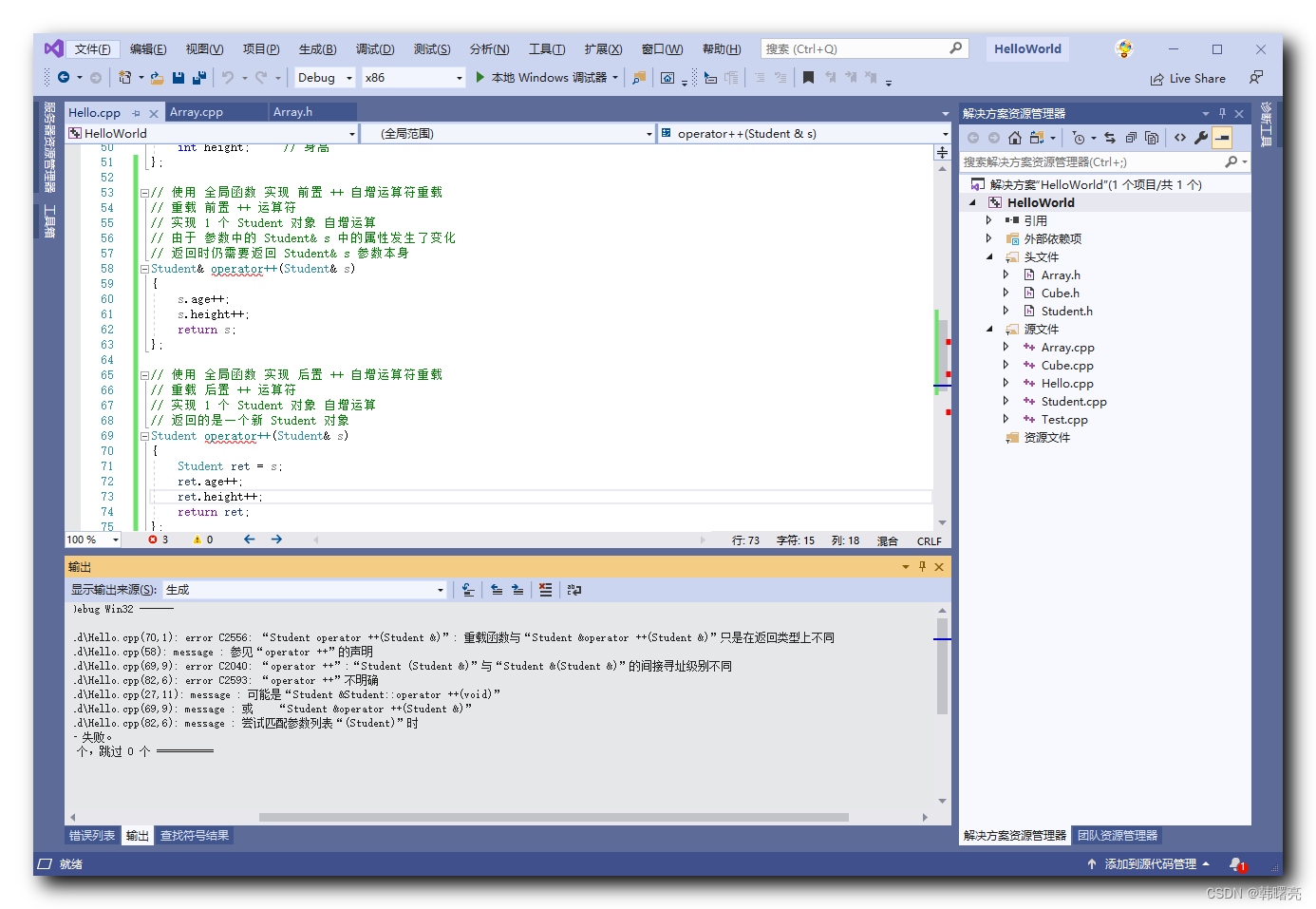
【C++】运算符重载 ⑥ ( 一元运算符重载 | 后置运算符重载 | 前置运算符重载 与 后置运算符重载 的区别 | 后置运算符重载添加 int 占位参数 )
文章目录 一、后置运算符重载1、前置运算符重载 与 后置运算符重载 的区别2、后置运算符重载添加 int 占位参数 上 2 2 2 篇博客 【C】运算符重载 ④ ( 一元运算符重载 | 使用 全局函数 实现 前置 自增运算符重载 | 使用 全局函数 实现 前置 - - 自减运算符重载 )【C】运算符…...

538. 把二叉搜索树转换为累加树
题目描述 给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。 提醒一下,二叉搜索树满足下列约束…...

java8日期时间工具类
【README】 1)本文总结了java8中日期时间常用工具方法;包括: 日期时间对象格式化为字符串;日期时间字符串解析为日期时间对象;日期时间对象转换; 转换过程中,需要注意的是: Instan…...

算法-动态规划/trie树-单词拆分
算法-动态规划/trie树-单词拆分 1 题目概述 1.1 题目出处 https://leetcode.cn/problems/word-break/description/?envTypestudy-plan-v2&envIdtop-interview-150 1.2 题目描述 2 动态规划 2.1 解题思路 dp[i]表示[0, i)字符串可否构建那么dp[i]可构建的条件是&…...

React框架核心原理
一、整体架构 三大核心库与对应的组件 history -> react-router -> react-router-dom react-router 可视为react-router-dom 的核心,里面封装了<Router>,<Route>,<Switch>等核心组件,实现了从路由的改变到组件的更新…...

python-pytorch 利用pytorch对堆叠自编码器进行训练和验证
利用pytorch对堆叠自编码器进行训练和验证 一、数据生成二、定义自编码器模型三、训练函数四、训练堆叠自编码器五、将已训练的自编码器级联六、微调整个堆叠自编码器 一、数据生成 随机生成一些数据来模拟训练和验证数据集: import torch# 随机生成数据 n_sample…...
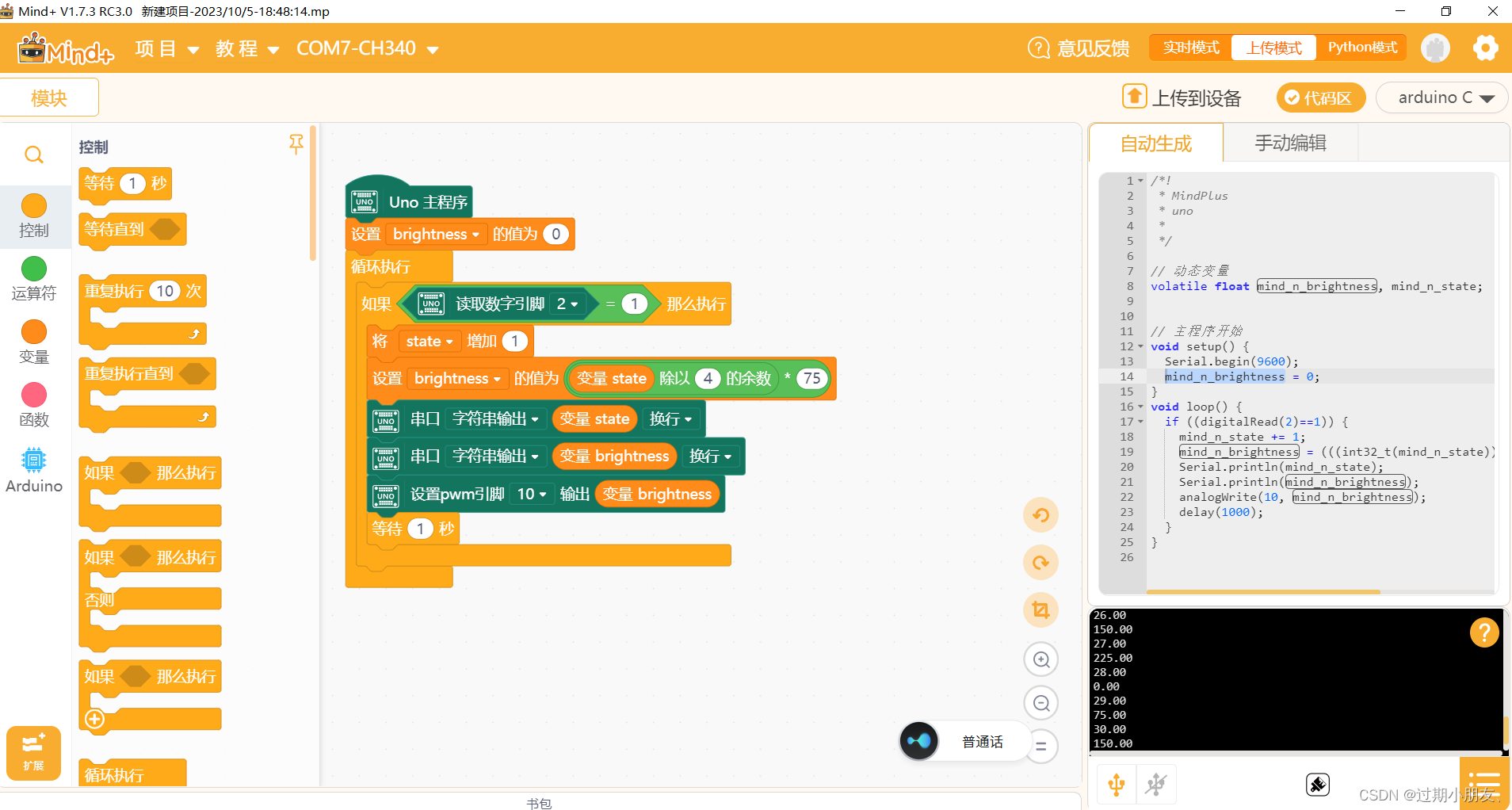
制作 3 档可调灯程序编写
PWM 0~255 可以将数据映射到0 75 150 225 尽可能均匀电压间隔...

源码分享-M3U8数据流ts的AES-128解密并合并---GoLang实现
之前使用C语言实现了一次,见M3U8数据流ts的AES-128解密并合并。 学习了Go语言后,又用Go重新实现了一遍。源码如下,无第三方库依赖。 package mainimport ("crypto/aes""crypto/cipher""encoding/binary"&quo…...

CSDN Q: “这段代码算是在STC89C52RC51单片机上完成PWM呼吸灯了吗?“
这是 CSDN上的一个问题 这段代码算是在STC89C52RC51单片机上完成PWM呼吸灯了吗,还是说得用上定时器和中断函数#include <regx52.h> 我个人认为: 效果上来说, 是的! 码以 以Time / 100-Time 调 Duty, 而 for i loop成 Period, 加上延时, 实现了 PWM周期, 虽然…...
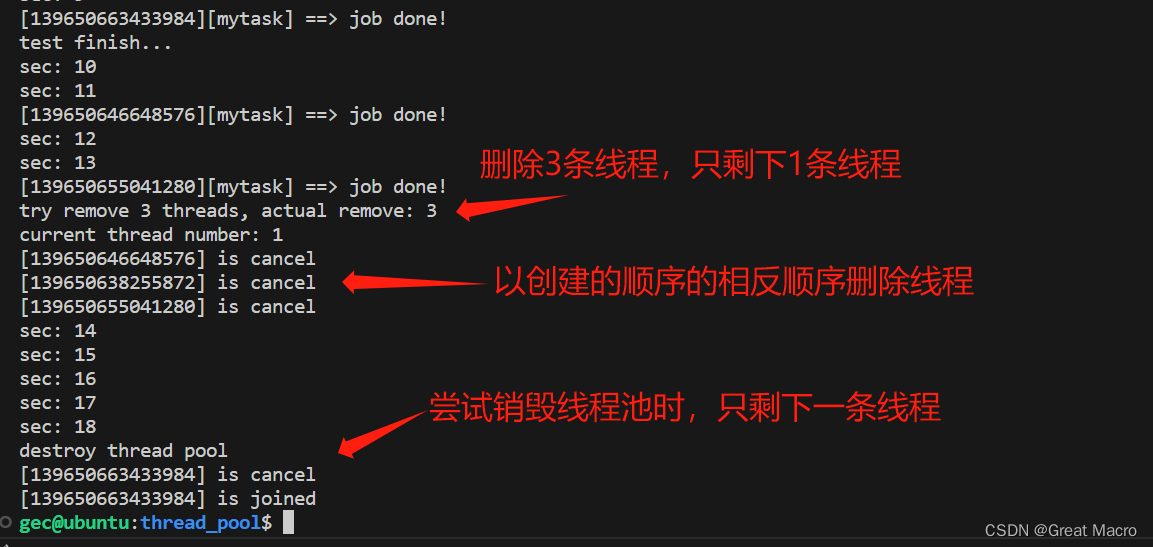
Linux系统编程系列之线程池
Linux系统编程系列(16篇管饱,吃货都投降了!) 1、Linux系统编程系列之进程基础 2、Linux系统编程系列之进程间通信(IPC)-信号 3、Linux系统编程系列之进程间通信(IPC)-管道 4、Linux系统编程系列之进程间通信-IPC对象 5、Linux系统…...

Linux CentOS7 vim多文件与多窗口操作
窗口是可视化的分割区域。Windows中窗口的概念与linux中基本相同。连接xshell就是在Windows中新建一个窗口。而vim打开一个文件默认创建一个窗口。同时,Vim打开一个文件也就会建立一个缓冲区,打开多个文件就会创建多个缓冲区。 本文讨论vim中打开多个文…...

SPI 通信协议
1. SPI通信 1. 什么是SPI通信协议 2. SPI的通信过程 在一开始会先把发送缓冲器的数据(8位)。一次性放到移位寄存器里。 移位寄存器会一位一位发送出去。但是要先放到锁存器里。然后从机来读取。从机的过程也一样。当移位寄存器的数据全部发送完。其实…...
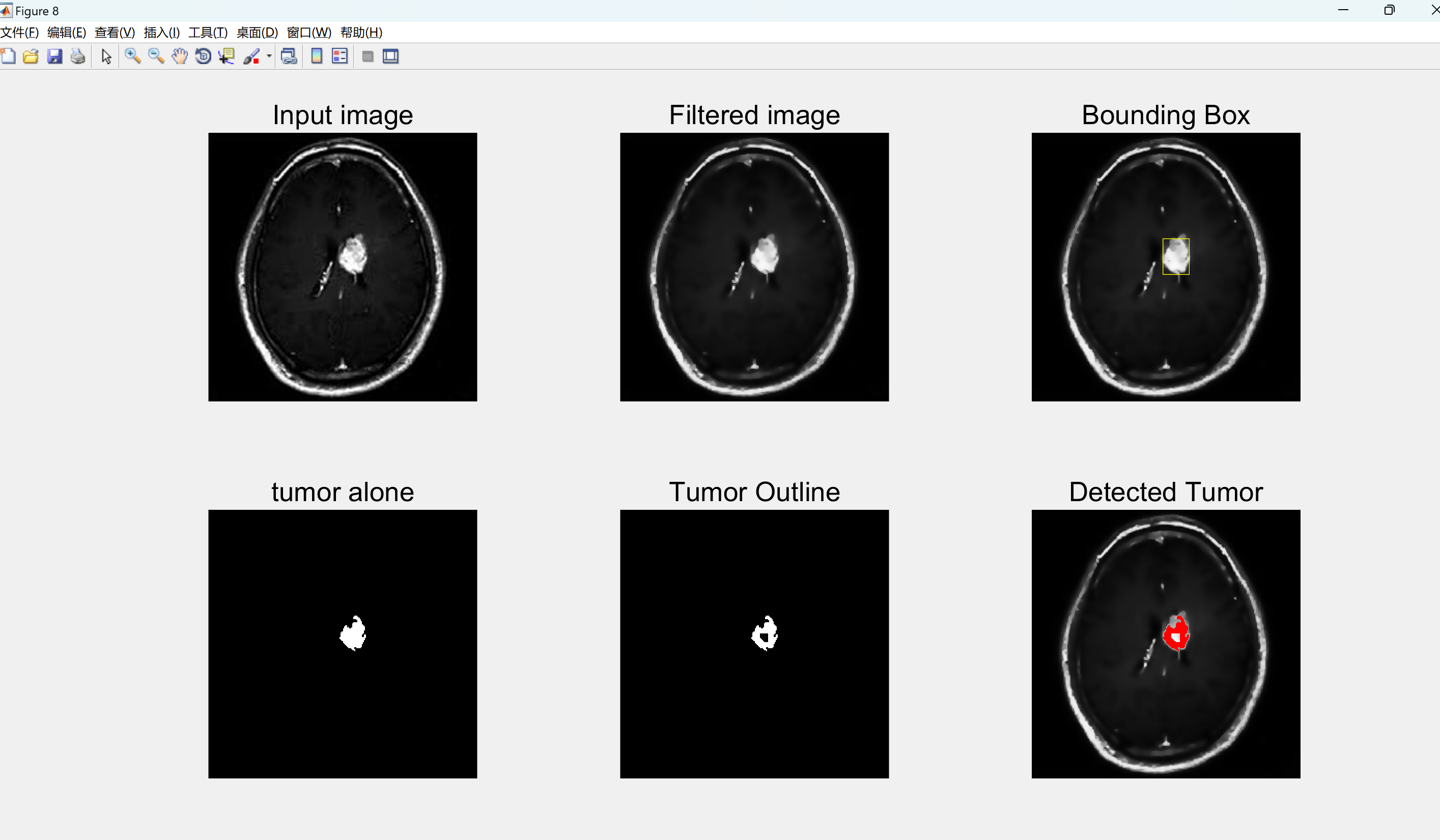
【图像处理】使用各向异性滤波器和分割图像处理从MRI图像检测脑肿瘤(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
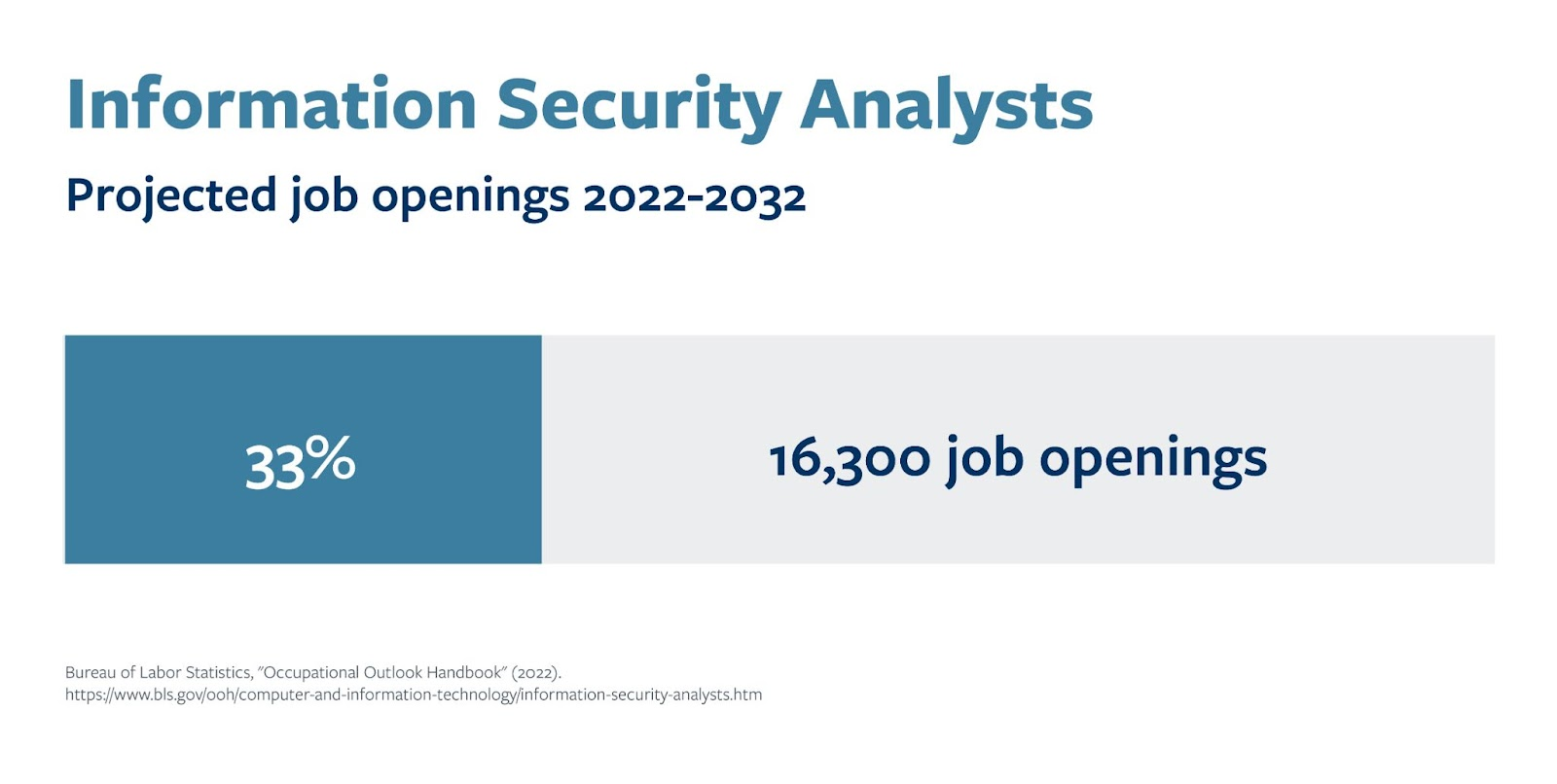
5个适合初学者的初级网络安全工作,网络安全就业必看
前言 网络安全涉及保护计算机系统、网络和数据免受未经授权的访问、破坏和盗窃 - 防止数字活动和数据访问的中断 - 同时也保护用户的资产和隐私。鉴于公共事业、医疗保健、金融以及联邦政府等行业的网络犯罪攻击不断升级,对网络专业人员的需求很高,这并…...

Kafka核心原理
1、Topic的分片和副本机制 分片作用: 解决单台节点容量有限的问题,节点多,效率提升,吞吐量提升。通过分片,将一个大的容器分解为多个小的容器,分布在不同的节点上,从而实现分布式存储。 分片…...

探秘前后端开发世界:猫头虎带你穿梭编程的繁忙街区,解锁全栈之路
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...
